Fenomene aeroelastice statice

Fenomene aeroelastice statice

1.Principalele fenomene aeroelastice statice

Prin deformatia elastic a suprafetei portante, atitudinea acestuia fata de curentul de aer se modifica, schimbandu-se in consecinta si valoarea fortelor aerodinamice. Aceasta interactiunea poate conduce la diferite tipuri de fenomene aeroelastice statice.

Schimbarea fortelor aerodinamice ca urmare a deformatiilor initiale are drept consecinta aparitia unei noi deformatii, fenomenul continuand pana la ruperea suprafetei pornate sau pana la o anumita deformatie limita. Fenomenul poarta numele de divergenta aeroelastica.

Prin determinarea deformatiilor limita ce se obtin, rezulta o distributie finala a sarcinilor aerodinamice. Aceasta distributie se numeste repartitia aeroelastica a portantei.

Exista deci o viteza la care sarcinile aerodinamice depasesc pe cele elastice, deformatia continuand pana la rupere. Peste aceasta viteza de divergenta, fenomenul este divergent, ajungandu-se la amplitudini mari.

Mai exista fenomene care se refera la manevrabilitatea si stabilitatea aparatului de zbor. Dispozitivele care asigura acest lucru sunt suprafete portante, capabile sa produca momente fata de cele trei axe de rotatie. Deformatiile elastice ale structurii de suport a acestor suprafete de comanda pot avea diferite efecte. Este astfel posibil sa apara o accentuare a efectelor comenzilor, o atenuare a acestui efect, o anulare sau chiar o inversare a lor.

Pentru avioane mici de mica viteza sau pentru avioane de mare viteza cu aripa dreapta, atingerea vitezei critice de divergenta este catastrofala, conducand la ruperea aproape sigura a aripilor. Repartitia aeroelastica pentru aceleasi tip de aripi face ca, datorita deformatiilor, sarcinile sa fie mai mari spre extremitatile aripilor, conducand la o redistribuire a sarcinilor aerodinamice.

Pentru aripi in sageata, sageata spre inainte accentueaza mult pericolul de aparitie a fenomenului de divergenta, acesta producandu-se pentru viteze mici. Aripa in sageata, cu sageata spre inapoi nu prezinta practic    pericol de divergenta, viteza critica fiind foarte mare.

Determinarea ecuatiilor de miscare

Din punct de vedere elastic aripa este aproximata cu o bara avand rigiditatile la incovoiere si torsiune cunoscute.

Din punct de vedere masic si inertial lucrurile sunt mai complicate, in sensul ca evaluarea caracteristicilor inertiale necesita determinarea unor momente de inertie de ordin I si II (static si dinamic) in raport cu axa elastica.

Masa totala

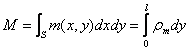
unde     este masa distribuita pe unitatea de anvergura a aripii

Axa centrelor de presiune este la distanta e fata de AE , pozitiva spre BA.

In cazul unghiului sageata se va lua axa elastica cu unghiul sageata 0.

Deformatiile aripii sunt caracterizate de functiile h(t,y) si (t,y). Aceste deformatii vor fi folosite in cele ce urmeaza pentru a determina ecuatiile de miscare intr-o forma convenabila si apoi pentru rezolvarea problemei de divergenta si flutter.

Determinarea ecuatiilor de miscare se face dupa Lagrange, considerand initial ca nu exista forte disipative de natura structurala.

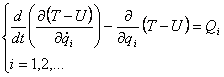
T - energia cinetica exprimata in functie de coordonata generalizata     si de viteza generalizata

U - energia potentiala de deformatie elastica exprimata in functie de     si

Q_i - fortele generalizate corespunzatoare coordonatelor generalizate; provin din lucrul mecanic al fortelor exterioare de natura aerodinamica, masica etc.

In cazul modelului:     si

Astfel:

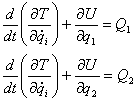
La aripa modelata

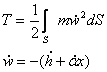
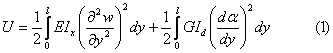
unde     inseamna in virtutea relatiei

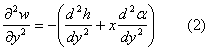
Pentru a putea folosi formalismul ecuatiilor Lagrange, cele 2 energii, ca si lucrul mecanic al fortelor exterioare de natura aerodinamica si masica, trebuie aproximate in functie de un set de coordonate generalizate.

In expresiile anterioare apare w(t,x,y) care este inlocuita prin functia h(t,y) si (t,y) care sunt definite pentru .

O modalitate de rezolvare a unei probleme este sa consideram ca     in care functiile f_h sunt cunoscute.

In mod similar:

- se numesc functii de forma sau de interpolare

Daca introducem astfel de dezvoltari in T si U, aceasta separare a variabilelor ne va conduce la identificarea coordonatelor generalizate.

T va depinde de derivatele in raport cu timpul ale lui q si q_h.

U va depinde de derivatele in raport cu y ale lui f_h si f

In final vom ajunge la identificarea coordonatelor generalizate.

Rezulta:

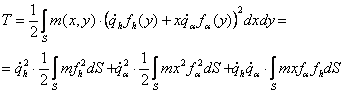
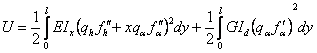
inlocuim cu: q₁ = q_h si q₂ = q

Avem :

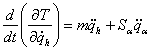
Astfel :

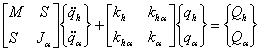
Putem marca similitudinea cu sectiunea tipica din punct de vedere al semnificatiei termenilor.

M - matricea maselor generalizate

K - matricea rigiditatilor generalizate

Fortele generalizate

Fortele exterioare care actioneaza asupra aripii sunt: aerodinamice si masice.

Pentru studiul fenomenelor de tip instabilitate statica si dinamica, putem determina fortele generalizate retinand numai contributiile acelor termeni din fortele aerodinamice si masice care depind numai de coordonatele generalizate q_h, q si derivatele in raport cu timpul.

In concordanta cu aproximarea de bara putem presupune ca din punct de vedere aerodinamic sunt cunoscute caracteristicile aerodinamice distribuite in sensul anvergurii.

Cum C_mF este o caracteristica independenta de incidenta, putem sa luam in considerare la scrierea fortelor generalizate numai efectul portantei.

Prin urmare, lucrul mecanic al fortelor exterioare de natura aerodinamica datorat unei deplasari virtuale w este:

P(y)x - moment dat de portanta fata de ce

Identificand coeficientii lui q_h si q

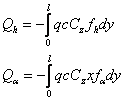
unde :

3.Studiu teoretic al divergentei aeroelastice

Pentru coeficientul de portanta vom considera

Astfel:

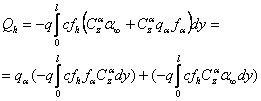
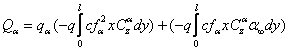
In casul static primul termen corespunzator matricei maselor [M] = 0

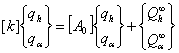
cu:

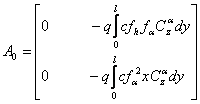
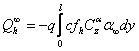
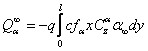
Problema de valori proprii pentru sistemul omogen va fi

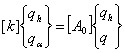
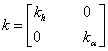
unde rigiditatile se calculeaza cu integralele

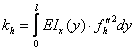
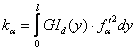
si functiile de forma

Matricea corespunzatoare fortelor de portanta

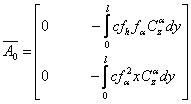
unde :

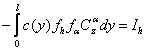
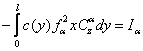
4.Calculul vitezei de divergenta a avionului

Calculul propriu-zis al vitezei de divergenta dupa cum urmeaza:

function integ = integ(ss);

integ = (ss(1)+*(ss(2)+ss(3)+ss(4)+ss(5)+ss(6)+

ss(7)+ss(8)+ss(9)+ss(10)+ss(11))+ss(12))/;

fh=sin(pi/2*Y/be);

fa=fh;

%Calculul integralei Kh cu formula trapezelor

fh2=(pi/(2*be))^2*fh;

dd=EIx.*fh*fh2;    Kh=be/11*Integ(dd);

%Calculul integralei Ka

fa1=-pi/(2*be)*cos(pi/2*Y/be);

ss=GJd.*fa1.*fa1;    Ka=be/11*Integ(ss);

%Calculul integralei Ih

aa=Cz*c.*fh.*fa;    Ih=be/11*Integ(aa);

%Calculul integralei Ia

bb=Cz*fa.*fa.*e;    Ia=be/11*Integ(bb);

%Calculul matircei Kha

fa2=(pi/(2*be))^2*fa;

ee=EIx.*fh*fa*e;    Kha=be/11*Integ(ee);

%Matricea K

K=[Kh Kha

Kha Ka];

%Matircea Ao

Ao=[ 0 -Ih

0 -Ia];

%Matricea corespunzatoare valorilor proprii A

A=inv(K)*Ao;

vp=eig(A);

q=min(1./vp); ro=56;

V=sqrt(2*q/ro)

Se obtine viteza de divergenta : Vd = 3242 m/s