Rezistenta echivalenta a circuitelor cu surse comandate

Rezistenta echivalenta a circuitelor cu surse comandate

Frecvent se cere determinarea rezistentei echivalente in raport cu doua borne a unui circuit ce contine surse comandate. La circuitele ce contin surse comandate este dificil sa se aplice regulile de simplificare a circuitelor studiate la conexiunile de rezistoare. O metoda simpla, dar precisa, de determinare a rezistentei echivalente este prezentata in Fig. 2.15.11.

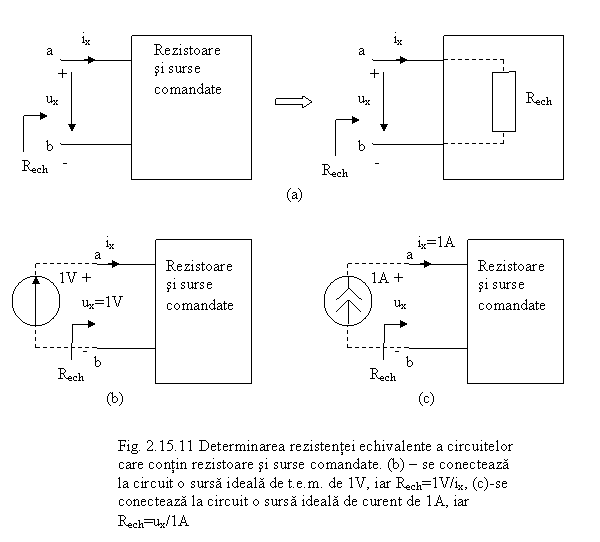
Echivalenta a doua circuite in raport cu doua borne presupune ca dependenta dintre u si i la cele doua borne ale celor doua circuite sa fie aceeasi In consecinta vom defini tensiunea u_x si curentul i_x la cele doua borne conform regulii de la receptor (conventia de circuit pasiv). Este important de mentionat faptul ca regula de asociere a sensurilor curentului si tensiunii de la receptor se aplica la cele doua borne a si b ale circuitului: curentul intra in circuit pe la borna + (plus) a tensiunii la borne a circuitului (Constituie o eroare asocierea sensurilor curentului si tensiunii invers fata de cel corespunzator conventiei de la receptor). In aceste conditii se defineste rezistenta echivalenta circuitului fata de cele doua borne ca raportul dintre tensiunea u_x si curentul i_x:

Se observa ca valorile numerice ale tensiunii si curentului nu sunt importante, doar raportul lor este important.

In Fig. 2.15.11b se prezinta un procedeu simplu, care usureaza determinarea rezistentei echivalente: se impune ca tensiunea u_x sa aiba valoarea de 1V (sau orice alta valoare) cu ajutorul unei surse de tensiune electromotoare ideale si se determina valoarea lui i_x. Apoi se calculeaza rezistenta echivalenta:

In Fig. 2.15.11c se prezinta un alt procedeu: se impune ca i_x sa aiba valoarea de 1A ( sau orice alta valoare) cu ajutorul unei surse ideale de curent si se determina valoarea tensiunii u_x. Valoarea rezistentei echivalente va fi :

Alegerea unuia dintre cele doua procedee prin impunerea lui u_x sa i_x este oarecum arbitrara si va conduce la acelasi rezultat. Totusi daca una dintre constrangerile mentionate va conduce la impunerea unei valori pentru variabila de control a sursei comandate, atunci acea alegere va facilita determinarea rezistentei echivalente. Acest lucru se va vedea in exemplele prezentate mai departe.

O posibilitate generala de determinare a rezistentei echivalente este aceea de scriere a ecuatiilor posibile pentru circuitul dat cu ajutorul teoremelor lui Kirchhoff, iar apoi sa se elimine treptat necunoscutele din ecuatiile sistemului rezultant pana ce ramane o singura ecuatie de forma:

u_x = f(R_k, α,β,γ,σ) i_x

unde f(R_k, α,β,γ,σ) este o expresie ce depinde de rezistentele din circuitul dat si de constantele surselor comandate din circuit. Valoarea rezistentei echivalente a circuitului va fi:

R_ech = = f(R_k, α,β,γ,σ)

Exemplul 6

Sa se determine rezistenta echivalenta in raport cu bornele a si b a circuitului din Fig. 2.15.12a.

Solutie

Date numerice: R₁ = 3Ω, σ = 2

Daca se aplica la bornele a si b o sursa ideala de tensiune electromotoare de 1 V , in felul acesta se va forta valoarea curentului i_y prin rezistorul R₁, care este variabila de control pentru sursa comandata. Curentul i_y va fi:

Cu aceasta valoarea curentului debitat de sursa de curent comandata va fi σ i_y = A. Aplicand teorema I a lui Kirchhoff in nodul de sus avem:    i_x = i_y + σ i_y = 1 A

Prin urmare, rezistenta echivalenta va fi:

O alta posibilitate de determinare a rezistentei echivalente este sa scriem pentru circuitul dat ecuatiile pe baza teoremelor lui Kirchhoff:

i_x = i_y + σ i_y u_x = i_y R₁

Inlocuind pe i_y din prima ecuatie in a doua, se obtine succesiv: ,

Rezistenta echivalenta a circuitului este:

Inlocuind valorile numerice date se obtine aceeasi valoare R_ech = 1Ω. Se observa ca aplicarea metodei teoremelor lui Kirchhoff pentru eliminarea celorlalte necunoscute ne da posibilitatea sa obtinem o expresie generala pentru rezistenta echivalenta.