STUDIUL RETELEI TRIFAZATE IN TRIUNGHI

STUDIUL RETELEI TRIFAZATE IN TRIUNGHI

I. Consideratiuni teoretice

Consideram un receptor trifazat format din trei rezistente ohmice legate in triunghi si alimentat cu un sistem de tensiuni de linie simetric. Se numeste sistem simetric un sistem de tensiuni, egale in modul si avand defazaje egale intre ele cu 2π m unde m este numarul de faze. Numim tensiune de linie, tensiunea masurata intre doua sfarsituri de faza succesive (de exemplu, tensiunile U₁₂, U₂₃, U₃₁ masurate intre fazele 1 si 2, 2 si 3 si 3 si 1).

Tensiunea de faza este tensiunea masurata intre inceputul si sfarsitul fazei respective si se noteaza cu U₁, U₂, U₃ sau U_f. In cazul unei conexiuni in triunghi a receptorului tensiunile de linie sunt egale cu cele de faza si deci intre tensiuni exista relatia

U_l = U_f

iar intre curenti

I_l = I_f√3

Daca se noteaza cu I₁, I₂ si I₃ curentii de linie si I₁₂, I₂₃ si I₃₁ curentii de faza. Intre cele doua feluri de curenti exista relatiile

I₁ + I₂ + I₃ = 0

I₁ = I₁₂ I₃₁

I₂ = I₂₃ I₁₂

I₃ = I₃₁ I₂₃

Deoarece receptorul din lucrarea noastra este pur rezistiv si sistemul de tensiuni cu care l alimentam este simetric, curentii de faza au aceeasi directie cu tensiunile de faza U₁₂, U₂₃, si U₃₁ (figura 1). Translatand vectorii tensiunilor si curentilor se obtine o stea echivalenta ca in figura 2.

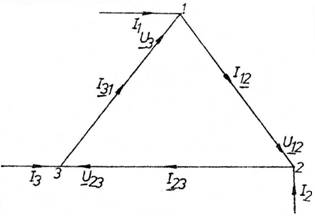
Fig.1

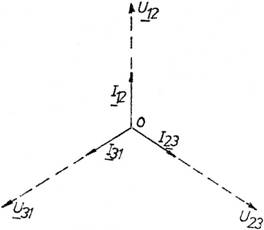
Fig.2

In functie de natura receptorului se disting doua situatii

a) Receptor in triunghi dezechilibrat. In acest caz diagrama fazoriala a curentilor este cea din figura 3 (dezechilibrata).

Se observa ca daca cunoastem valorile curentilor I₁₂, I₂₃, si I₃₁ (ce se masoara cu ampermetrele) putem determina curentii de linie I₁, I₂ si I₃ iar valorile obtinute prin calcul se pot compara cu cele obtinute prin masurare.

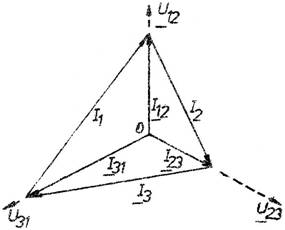
Fig. 3

b) Receptor in triunghi echilibrat. In cazul receptorului echilibrat curentii de faza I₁₂ = I₂₃ = I₃₁ si deci si curentii de linie vor fi egali intre ei I₁ = I₂ = I₃.

Prin urmare diagrama fazoriala este cea din figura 4.

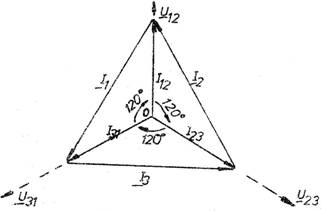
Fig. 4

Deoarece curentii de linie si de faza formeaza sisteme simetrice este suficient sa calculam numai un curent de faza si numai un curent de linie. Ceilalti curenti se obtin din acestia luand un defazaj corespunzator.

Se observa ca intre curentii de linie si de faza se obtine relatia

I_l = I_f√3

II. Scopul lucrarii

Lucrarea are drept scop studierea comportarii unui receptor pur rezistiv trifazat in triunghi atunci cand la bornele lui se aplica un sistem de tensiuni simetric. Se vor vor masura curentii de linie si de faza si rezultatele obtinute se vor compara cu cele rezultate din calcul. De asemenea, se vor compara curentii de linie si de faza masurati sau calculati.

III. Schema de montaj folosita

Pentru efectuarea lucrarii se va realiza montajul de mai jos unde

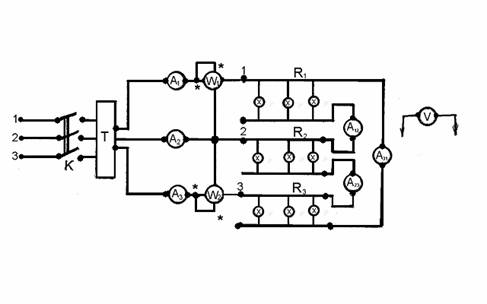
K intrerupator trifazat

A₁, A₂, A₃, A₂₂, A₂₃, A₃₁ ampermetre electromagnetice 0 10 A clasa de precizie 0,5

V voltmetru c.a. feromagnetic scara 260 V clasa de precizie 0,5

R₁, R₂, R₃ reostate trifazate cu lampi de 220 V existente in laborator

T transformator trifazat coborator de tensiune 380 V 220 V

W₁, W₂ - wattmetre electrodinamice e-75-150-300-450 si 0 - 2,5 - 5 A de c.a.

IV. Chestiuni de studiat

1. Functionarea retelei in triunghi cu sarcina echilibrata prin care se vor verifica relatiile dintre curentii de linie si de faza.

I_l = I_f√3

2. Functionarea retelei in triunghi incarcata cu sarcina dezechilibrata pentru urmatoarele situatii:

R₁ = R₂ ≠ R₃

R₁ ≠ R₂ ≠ R₃

R₁ = R₂ = ∞ si R₃ ≠ 0

Se vor compara valorile masurate ale curentilor de linie cu cele determinate grafic prin calcul.

3. Masurarea puterilor absorbite de catre fiecare faza, cu ajutorul wattmetrului si compararea lor cu cele determinate prin calcul.

V. Modul de lucru

De obicei la montajul in triunghi tensiunile de linie sunt egale cu cele de faza, adica U_l = 380 V si pentru a nu se arde becurile reostatelor care sunt de 220 V s a introdus in montaj un transformator coborator de tensiune. Acesta coboara tensiunea de la 380 V la 220 V. Inainte de inceperea lucrarii toate becurile trebuie sa fie scoase.

1. Functionarea retelei trifazate in triunghi incarcata cu sarcina echilibrata. Se inchide intrerupatorul K si se aprinde pe fiecare faza un numar de becuri egal, astfel ca indicatiile ampermetrelor A₁₂, A₂₃ si A₃₁ sa fie identice. Se observa ca si indicatiile ampermetrelor A₁, A₂ si A₃ sunt egale.

Se masoara cu voltmetrul V tensiunile intre punctele si 3 - 1. Aceste tensiuni reprezinta atat tensiunile de linie cat si cele de faza. Toate valorile se trec in tabelul 1. Intre curentii de linie si de faza se constata egalitatea

I_l = I_f√3

Se va masura cu ajutorul wattmetrului puterea totala absorbita de circuit si se va compara cu cea rezultata prin calcul conform relatiei

P_calc. = 3U₁₂ ∙ I₁₂ = 3U_fI_f = U_fI_l√3

Pentru masurarea puterii cu wattmetru se va utiliza metoda celor doua wattmetre si puterea totala va fi egala cu suma indicatiilor wattmetrului pentru cele 2 cazuri.

P_mas = P₁₂ + P₂₃

Pentru masurarea puterii curentii trebuie sa aiba valori mai mici de 5 A (atat suporta bobina de curent a wattmetrului).

De asemenea, se va observa ca aceasta putere este egala cu suma puterilor absorbite de cele trei faze ale receptorului. Prin urmare trebuie sa avem

P_mas = P_calc.

Se va construi o diagrama de fazori ca in figura 4.

Tabelul 1.

2. Functionarea retelei in triunghi incarcata cu sarcina dezechilibrata.

Se realizeaza fiecare din cele trei sarcini dezechilibrate

a) Cazul cand R₁ = R₂ si R₃ variabil.

Mentinand valorile curentilor de pe doua faze (I₁₂ = I₂₃) se scot sau se introduc cateva becuri pe baza a treia si se citesc indicatiile ampermetrelor care se noteaza in tableul 2.

Se citesc si puterile indicate de wattmetre. Se scot apoi toate becurile de pe faza a treia realizand R₃ = ∞ si I₂₃ = 0. Se citesc curentii de linie si de faza si de asemenea, se masoara puterile la wattmetre. Pentru ambele situatii se vor construi cate o diagrama de fazori, ca in figura 3.

b) Cazul cand R₁ ≠ R₂ ≠ R₃. Reteaua este complet dezechilibrata. Se citesc curentii de linie si de faza si tensiunile de faza cu ajutorul voltmetrului V. De asemenea, se vor citi indicatiile wattmetrelor. Suma puterilor pe cele trei faze trebuie sa fie egala cu suma indicatiilor celor doua wattmetre, adica

P₁ + P₂ + P₃ = P_mas. sau

3U_fI_f = P₁₂ + P₂₃

Se va construi diagrama de fazori si se va verifica vectorial ca suma curentilor de linie este egala cu zero ca si in cazul a.

c) In acest caz se vor scoate becurile de pe fazele 1 si si se vor observa ca I₁₂ = I₂₃ = 0 iar I₃₁ ≠ 0. Se vor citi indicatiile wattmetrelor si ampermetrelor si rezultatele se vor trece in tabelul 2. Se va face diagrama fazoriala a curentilor.

Tabelul 2.

VI. Indicatii suplimentare pentru intocmirea referatului

Toate diagramele se vor executa pe hartie milimetrica la scara.

Se va acorda mare atentie la citirea wattmetrelor urmarindu-se ca la inceputul lucrarii sa se aleaga scarile maxime pentru curent si tensiune, iar curentii din laturi se vor verifica si

cu ajutorul ampermetrelor respective.

Se va observa egalitatea dintre puterile masurate si cele calculate si se vor trage concluziile corespunzatoare.

Se va explica de ce atunci cand R₁ = ∞ curentii I₁ = I₃₁ si I₂ = I₂₃.

VII. Intrebari de control

1. Ce relatii exista intre curentii de linie si de faza la montajul in triunghi?

2. Ce relatii exista intre tensiunile de linie si de faza la montajul in triunghi echilibrat?

3. Care este expresia puterii absorbite de laturile circuitului in cazul montajului in triunghi echilibrat?

4. Cum se construieste diagrama de fazori pentru curentii de linie la montajul in triunghi dezechilibrat?

5. Ce valori vor avea curentii din laturile montajului in triunghi echilibrat daca la un moment dat se intrerupe un conductor de linie? Dar daca se intrerup simultan doua conductoare de linie?

6. Ce valori vor avea curentii de faza si de linie dintr un montaj in triunghi echilibrat daca la un moment dat se intrerupe o faza?