Calculul campului termic stationar unidimensional. Exemplu - cazul electrodului sferic.

Calculul campului termic stationar unidimensional. Exemplu - cazul electrodului sferic.

Aceasta sectiune este destinata calcului campului termic intr-un electrod sferic folosit in procesul de electroeroziune (Fig. 3).

Fig. 3. Campul termic intr-un electrod sferic folosit

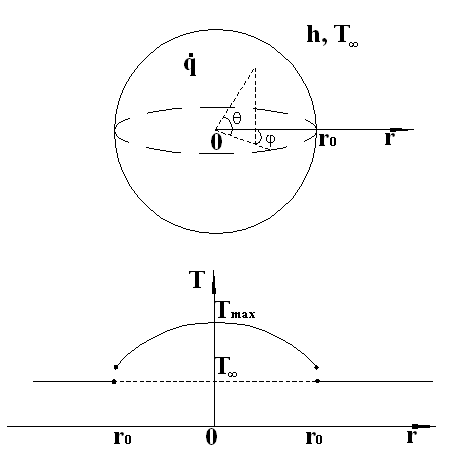
in procesul de electroeroziune.

Datorita efectului Joule, se genereaza caldura in volumul acestuia . Caldura se disipa catre mediul ambiant, aflat la temperatura T_∞, prin convectie, h fiind coeficientul de transfer termic. La un moment dat, dupa o perioada tranzitorie, se atinge regimul de echilibru (campul termic este stationar in timp). In acest exemplu se va calcula campul termic in conditii de echilibru. Rezolvarea problemei cere parcurgerea urmatorilor pasi [2]:

Pasul 1: Se alege sistemul de coordonate care se potriveste cel mai bine cazului studiat si se identifica variabilele independente ce determina campul termic T

Se alege un sistem de coordonate sferice si se cauta functia T(r,θ,j,t) ca functie de coordonatele cilindrice si timpul t.

Pasul 2: Se scrie forma cea mai potrivita a ecuatiei transferului termic.

Considerand campul termic stationar () si axi-simetric (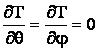), vom stabili campul termic T(r) ca functie de raza, r. In aceste conditii, ecuatia transferului termic devine:

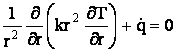. (27)

In cele ce urmeaza, se considera ca materialul corpului considerat este omogen si ca are o conductivitate termica ce nu depinde de temperatura, deci, k=constant. Avand in vedere ca T este functie numai de o singura variabila, derivatele partiale din ecuatia (1) devin derivate totale. In consecinta, ecuatia (27) devine

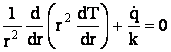. (28)

Pasul 3: Se obtine forma generala a ecuatiei transferului termic

Se integreaza ecuatia (28) si se defineste necunoscuta de integrare C₁

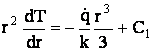. (29)

In continuare, se integreaza ecuatia rezultata, 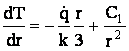, si se defineste a doua constanta de integrare, C₂

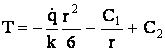. (30)

Aceasta este ecuatia generala a campului termic. Pentru a afla cele doua necunoscute, trebuiesc aplicate conditiile de contur.

Pasul 4: Se scriu conditiile de contur:

In cazul acestei probleme, se impun doua conditii de contur:

- conditia de simetrie a campului termic fata de axa z

la r=0; (31)

- conditia de transfer termic prin convectie la raza exterioara r₀

la r=r₀. (32)

Pasul 5: Se innlocuieste solutia generala a campului termic in conditiile de contur si se calculeaza constantele.

Aplicand ecuatia (31) in ecuatia (29), se obtine solutia

C₁=0 (33)

In acest stadiu al calculului, ecuatia generala a campului termic este 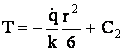. (34)

Inlocuind (34) in (32) se deduce

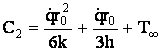. (35)

Pasul 6: Se introduc constantele obtinute in ecuatia generala a campului termic si se obtine solutia specifica problemei rezolvate.

Solutia generala a campului termic cautat este

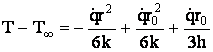. (36)

Pasul 7: Se studiaza solutia gasita. Se verifica corectitudinea ei.

Acest camp termic are o variatie de tipul celei prezentate in Fig.3: o distributie parabolica si cu maximul la r=0. Maximul campului termic este

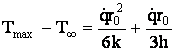. (37)

Pasul 8: Daca acest campul termic este corect stabilit, se poate afla fluxul termic, inlocuind solutia gasita in legea lui Fourier.

Inlocuind solutia (36) gasita, in legea lui Fourier, se obtine

. (38)

Cantitatea de caldura eliberata in mediu, la raza exterioara,

, (39)

este egala cu caldura degajata in volumul sferic al corpului studiat, asa cum era de asteptat. Aceasta confirma, inca o data, corectitudinea solutiei gasite.