Ecuatiile de functionare ale motoarelor de inductie in regim tranzitoriu

Ecuatiile de functionare ale motoarelor de inductie in regim tranzitoriu

a) Aspecte generale

Fenomenele de baza, destul de complexe, care au loc intr-un motor de inductie in regim stationar se regasesc si in cadrul regimului tranzitoriu. In acest din urma caz apar si o serie de fenomene suplimentare, cauzate, in principal, de variatiile de amplitudine ale unor marimi. Astfel, in expresiile fluxurilor totale intervin si componente datorate variatiilor de amplitudine ale curentilor prin diverse infasurari.

Bineinteles, aceste aspecte se reflecta intr-o crestere a complexitatii modelului matematic. Acest model se prezinta, de obicei, prin sase ecuatii de echilibru al tensiunilor (cate una pentru fiecare faza a infasurari statorice si rotorice) si o ecuatie de echilibru mecanic. Pentru a simplifica manipularea modelului mathematic se procedeaza in diverse moduri cum ar fi:

- utilizarea fazorilor spatiali (numiti si vectori spatiali) pentru diverse marimi (fluxuri, tensiuni curenti); un fazor spatial este o marime complexa ce reflecta efectul comun al valorilor instantanee ale marimilor de acelasi fel din cele trei faze statorice sau rotorice;

- utilizarea reprezentarilor in doua axe d-q (direct - cuadratura), ceea ce revine la a considera un model bifazat pentru masina trifazata; pentru fiecare armatura se scriu in acest caz cate doua ecuatii, inct modelul matematic contine 4 ecuatii de tensiuni. Daca intervin si componente homopolare, mai trebuie introduse si doua ecuatii pentru acestea (cate una pentru stator si respectiv pentru rotor); de precizat ca aceste componente nu influienteaza celelalte marimi, asa incat cele patru ecuatii mentionate anterior se trateaza separat;

- utilizarea reprezentarilor in complex, procedura intru-totul echivalenta cu precedenta, dar componentele d si q ale marimilor respective se interpreteaza drept parte reala respectiv imaginara a unei marimi complexe;

- utilizarea de reprezentari matricial - vectoriale, care sunt reprezentari echivalente pentru modelele bi s-au trifazate.

De mentionat ca reprezentarile bifazate sunt importante nu numai prin faptul ca permit o tratare mai simpla al modelului matematic, dar sunt utilizate efectiv in cadrul procedurilor moderne de control al acestor motoare, in sensul ca in cadrul controlerelor respective se opereaza cu marimi din reprezentarile bifazate.

Semnalam, de asemenea, existenta unui mare numar de modele, atat prin formele diferite mentionate mai sus, cat si prin faptul ca se pot utiliza sisteme de referinta raportate la marimile din stator, din rotor sau din intrefier. Uneori se prefera reprezentarea intr-un sistem referential general, care se poate apoi particulariza la oricare din cele trei categorii de referentiale ale masini de inductie.

Toate modelele mentionate se pot reprezenta si sub forma ecuatiilor de stare.

Complexitatea tuturor categoriilor de modele este ridicata si datorita faptului ca multi coeficienti din ecuatiile de tensiuni depind de vitezele relative dintre diverse marimi, ca rezultat al faptului ca rotorul se afla in miscare fata de stator. Din acest motiv, se prefera de multe ori sa se opereze cu doua scari de timp, avand in vedere faptul ca vitezele se modifica mult mai lent decat marimile electromagnetice. Ca atare, intr-o prima aproximare, se considera ca vitezele sunt constante si se determina variatiile curentilor si fluxurilor si apoi se fac reajustarile necesare pentru noile valori ale vitezelor etc. In felul acesta, ecuatiile de tensiuni sunt tratate ca fiind liniare, cu coeficienti constanti si apoi se tine seama de modificarea acestor coeficienti cu viteza.

In fine, ecuatia de miscare este neliniara, deoarece expresia cuplului motor contine produsul a doua marimi variabile. Ca atare, modelul matematic al motorului de inductie este neliniar si variant in timp. Studiul comportarii motorului de inductie in regim tranzitoriu se poate face doar prin simulare.

Metodele moderne de conducere implica prelucrarea modelului in timp real si aceasta se realizeaza prin aproximari pe portiuni, de exemplu, parcurgand urmatoarele etape principale:

considerand o anumita viteza rotorica constanta se stabilesc fluxurile si curentii la anumite momente de timp;

se calculeaza cuplul electromagnetic si se determina viteza rotorica din ecuatia de miscare;

se revine la prima etapa, inlocuind viteza rotorica cu noua valoare obtinuta.

In cele ce urmeaza se va face o serie de referiri la diversele categorii de modele, cu mentiuna ca o tratare mai explicita se prezinta in referatele de laborator L_11.

b) Ecuatiile de tensiuni ale masinii asincrone trifazate

Se face ipoteza ca infasurarile trifazate ale celor doua armaturi sunt simentrice, adica au aceleasi impedante si sunt dispuse astfel incat fac intre ele ungiuri electrice de 120 . De asemenea, se considera ca inductiile create la periferiile armaturilor au o repartitie sinusoidala (se neglijeaza armonicele; ele ar putea fi luate in considerare printr-o tratatre similara cu cea referitoare la armonica fundamentala).

Modelul mathematic contine 6 ecuatii de forma:

(1)

in care indicii k = s,r se refera la infasurarile statorice, respectiv rotorice, iar indicii j = a, b, c se refera la fazele a, b, c. In relatia (1), u_kj este tensiunea care se aplica fazei statorice j. Ne vom referi in continuare, cu precadere, la masinile cu rotorul in scurtcircuit, pentru care

(2)

In (1), i_kj(t) reprezinta curentul instantaneu prin infasurarea respectiva si evident, R_kj i_kj este caderea de tensiune pe rezistenta de faza considerata. y_kj (t) este valoarea instantanee a fluxului total care strabate spirele infasurarile respective.

Ultimul termen din (1) reprezinta deci o t.e.m. indusa si care este formata din t.e.m.ce apar prin inductie (autoinductie) datoritǎ variatiei curentilor prin infǎsurǎri si t.e.m. induse prin rotatie. Acestea din urmǎ se pot pune in evidentǎ prin expresii de aceeasi formǎ ca si primele, dar in acest caz, inductivitǎtile mutuale depind de pozitia relativǎ momentanǎ dintre infǎsurǎri si, ca atare, apare dependenta de viteza rotoricǎ.

Pentru faza a statoricǎ fluxul total se poate scrie:

(3)

In aceastǎ relatie i_sj si i_rj reprezintǎ curentii prin faza statoricǎ, respectiv rotoricǎ j (j = a,b,c), iar cu m_aj s-au notat inductivitǎtile dintre o anumitǎ fazǎ statoricǎ/rotoricǎ si faza a statoricǎ. De observat cǎ este inductivitatea proprie a fazei a statorice, aceeasi pentru toate fazele statorice. Cu m^s s-au notat inductivitǎti mutuale intre infǎsurǎri statorice, iar cu m^sr - inductivitǎti mutuale intre infǎsurǎri statorice si rotorice, acestea depinzand de unghiul pe care il face la un moment dat o axǎ de referintǎ rotoricǎ fatǎ de una statoricǎ.

Relatia (3) evidentiazǎ faptul cǎ fluxul total care strǎbate o infǎsurare este determinat de curenti prin toate cele sase faze. Pentru celelalte faze statorice, se exprima prin relatii similare, inlocuind corespunzǎtor indicele a cu b si respectiv c. In mod asemǎnǎtor se scriu expresiile fluxurilor rotorice, permutand in (3) indicii s si r. Cele sase relatii se pot exprima vectorial.

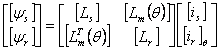(4)

in care sunt vectori tridimensionali (indicele q atasat la i_r marcheazǎ faptul cǎ rotorul este rotit cu unghiul q fatǎ de stator), iar [L_s],[L_r] si [L_m(q)] sunt matrice 3x3 ale inductivitatilor .

c) Utilizarea fazorilor spatiali

Sǎ notǎm cu g_a, g_b, g_c valorile instantanee ale unei aceleeasi mǎrimi (flux, curent, tensiune) corespunzǎtoare celor trei faze statorice sau rotorice. Luǎm ca referintǎ faza a si introducem vectorii corespunzǎtori, tinand cont de decalajul spatial de 2p

(5)

unde a exprimǎ operatorul de rotatie

(6)

Efectul comun al mǎrimilor de pe cele trei faze se poate exprima prin fazorul spatial (numit si vector spatial).

(7)

unde k_F este un coeficient; in functie de semnificatia care se atribuie unor mǎrimi, diversi autori folosesc pentru k_F valorile 1, 2/3 sau .

De remarcat cǎ doar pentru y se poate atribui o semnificatie fizicǎ concretǎ, corespunzand fluxului resultant al celor trei faze. Fazorii nu au o astfel de semnificatie, deoarece curentii /tensiunile pe cele trei faze nu se sumeazǎ in spatiu . Pentru acestia rǎmane doar o semnificatie de operator matematic, care exprimǎ efectul comun al mǎrimilor componente.

Ecuatiile de tensiuni statorice si rotorice exprimate pe baza fazorilor spatiali sunt:

(8)

(9)

d) Utilizarea unui model bifazat

Ca orice vector aflat intr-un plan (si anume, un plan perpendicular pe axa masinii), fazorul poate fi descompus dupa douǎ axe (directǎ - d si in cuadraturǎ - q), sau poate fi exprimat ca marime complexa.

Daca axa reala coincide cu axa d, vom scrie

(10)

In astfel de descompuneri, daca sistemul trifazat nu este echilibrat, pe langa componentele d si q apare si componenta homopolara

(11)

Ecuatiile de tensiuni ale masinii de inductie se scriu sub forma:

(12)

O ecuatie similara se scrie si pentru componentele pe axa q. De asemenea, apar si doua ecuatii similare pentru rotor.

La cele patru ecuatii se adauga, daca este cazul, ecuatii similare pentru componentele homopolare statorice si rotorice. Aceste componente depind de componentele d si q, dar nu le influenteaza, asa incat cele patru ecuatii de forma (12) pot fi tratate separat.

e) Exprimarea matriceal - vectoriala

Ecuatiile masinii bi sau trifazate se pot exprima matriceal - vectorial. De exemplu, pentru stator se poate scrie

, (13)

indicele t marcand faptul ca ecuatia se refera la un model trifazat. Componentele vectorului [u_s] sunt tensiunile pe faza u_sa, u_sb, u_sc. Similar - pentru [i_s] si [y_s

O relatie similara se scrie si pentru un model bifazat (marcand elementele respective, de exemplu, cu indicele b). Se poate folosi un model complet sau simplificat, folosind vectori de forma:

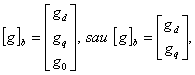cu g₀ - componenta homopolara

Observatii:

(1 ) In studiul motorului de inductie si chiar in aplicarea unor proceduri de control este necesar sa se treaca de la un tip de model la altul: de la tri la bifazat sau invers. De asemenea, apare necesitatea de a se face raportari la un acelasi referential; de exemplu, ecuatiile rotorice se raporteaza la stator, ceea ce se poate realiza intr-o maniera similara cu cea indicata la 3.3.2 pentru regimul stationar. In sfarsit, sa mai mentionam ca se fac transformari (rotiri) de axe, pentru sistemul bi sau trifazat.

Relatiile pentru toate aceste transformari se dau in referatul L - 11 - A.

(2 ) Uneori se exprima ecuatiile masinii sub forma ecuatiilor de stare; acestea se pot prezenta, de asemenea, sub diverse forme. Utilizarea ecuatiilor de stare este utila mai ales in cazul folosirii anumitor proceduri de estimare a marimilor din sistem (fluxuri, viteza). -(A se vedea L - 11 - D).

(3 ) De multe ori se apeleaza la exprimarea modelului intr-un referential oarecare. Relatiile anterioare au fost scrise intr-un referential fix pentru stator si unul fix fata de rotor, deci variabil fata de stator. Este necesara exprimarea tuturor relatiilor fata de acelasi referential (de exemplu fix, sau care se roteste cu viteza rotorului sau a campului din intrefier. Alteori se prefera ca referentialul sa fie oarecare (de exemplu, sa faca un unghi l fata de axa de referinta statorica), putand fi apoi particularizat la unul din referentialele mentionate. Aceasta se poate obtine prin rotirea sistemului de axe, de exemplu:

, sau (14)

Cu aceasta, ecuatiile fazorilor spatiali statorici si rotorici devin:

(15)

(16)

in care w si reprezinta vitezele unghiulare ale rotorului si respectiv ale sistemului de referinta:

. (17)

Ecuatia (15) rezulta din (8) in urma transformarii (14); ultimii doi termeni din (15) rezulta din efectuarea derivatei din (8), tinand cont ca l este variabil. Pentru ecuatia rotorica se are in vedere ca acesta face unghi q cu statorul, asa ca in loc de l va apare l q in (14); de asemenea, se inlocuieste cu si rezulta in final (16).

f. Cuplul electromagnetic si ecuatia de miscare a sistemului de actionare

Ecuatia de miscare a sistemului de actionare este:

(18)

in care este cuplul electromagnetic al motorului asincron, este cuplul rezistent produs in principal de masina de lucru, iar

(19)

este cuplul dinamic, fiind viteza rotorului.

Mai ramane de precizat expresia cuplului electromagnetic. Acesta poate fi exprimat in diverse moduri, in functie de componentele bi sau trifazate ale marimilor; expresia sa va contine un produs a doua marimi (flux, curent sau chiar t.e.m.) din stator, rotor sau intrefier. Aceasta expresie se poate deduce derivand energia cinetica in raport cu coordonata generalizata, sau din expresia puterii electromagnetice. De mentionat ca valoarea cuplului electromagnetic ramane aceeasi indiferent de sistemul de axe la care se raporteaza marimile in functie de care se exprima.

Astfel, expresia acestuia in functie de fluxul si curentul statoric/rotoric raportate la un referential care face unghiul l cu axa de referinta statorica este:

, (20)

, (20')

unde p este numarul de perechi de poli iar x marcheaza produsul vectorial. (Sa observam ca aceasta reprezinta o reflectare a cunoscutei legi , care exprima interactiunea dintre un curent si un camp magnetic). Modulul vectorului (20) este:

(21)

(21')

unde sunt unghiurile dintre vectorii si respectiv . Sa observam ca (21') este similara relatiei (31) de la paragraful 3.2.c (in (31) apare coeficientul 3 si nu 3/2 deoarece acolo se opereaza cu valorile efective). Relatia (21') exprima valoarea instantanee a cuplului si ea ramane valabila si in regim stationar, pentru care a fost dedusa (31).

Expresia (21') se mai poate scrie

(22)

unde este conjugata lui , sau

(23)

In adevar, scriind si (pentru simplificarea notatiilor s-a omis precizarea indicilor sλ), facand produsul din (22) si retinand numai partea imaginara, rezulta (23). De asemenea, daca exprimam componentele d si q ale marimilor, expresia (23) de scrie:

(cu α₁ si α₂ s-au notat unghiurile vectorilor ψ si i fata de axa d). Dar si deci

adica tocmai expresia (21).

Relatiile similare cu (22 ) si (23) se pot scrie si in raport cu marimile rotorice, pornind de la (21¢). De asemenea, se poate arata ca se obtin expresii similare daca se folosesc si alte combinatii de fluxuri si curenti apeland si la fluxul de magnetizare y_m :

(22")

Pentru fiecare din formele (22²) rezulta formele corespunzatoare de tipul (21) sau (23).

Sa observam ca fata de cazul masinii de c.c., la care

m = kyi , (24)

aici intervine in relatiile de forma (21) si sin(y,i). La masina de c.c. compensata vectorii y si i sunt ortogonali, asa incat sin(y, i) = 1 si nu mai apare in (24). Neortogonalitatea vectorilor y si i de la motorul de inductie se reflecta in aparitia a doi termini in expresiile de forma (23) ale cuplului. Aceasta face ca, in cazul acestei masini, cuplul si respectiv viteza sa poata fi mai dificil controlate.