| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
Transmisia mecanica de uz general formata din urmatoarele componente :
Un motor asincron , trufazat cu rotorul in scurtcircuit
O transmisie de curele cu profil trapezoidal
Redactor intr-o treapta cu angrenaj cilindric cu dinti drepti.
Transmisie de uz general
Electromotor (EM)
Roata de curea 1 (conducatoare)
Curea
Roata de curea 2 (condusa)
Arbore de intrare (1)
Arbore de iesire (2)
Roata dintata 1 (z1)
Roata dintata 2 (z2)
Rulment 1
Rulment 2
Carcasa
Roata de curea 1 se monteaza pe arboreal electromotorului , iar Roata de curea 2
se monteaza pe arborele 1 din redactor.
DATE INITIALE
Turatia de sincronism a motorului
nms= 750 [rot/min]
Momentul de iesire
Me = 130 [N∙m]
Turatia de iesire
ne = 155 [rot/min]
Perioada de timp
T = 1.5 ∙ 104 [h]
Cap.1 Alegerea tipului electromotorului
Calculul puterii de iesire
Pe = Me ∙ ω3 [W] = Me ∙ ω3 ∙ 10-3 [KW]
Pe = 2.11 [KW]
ω
e = 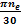
Calculul puterii motorului
Pmc
= 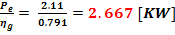
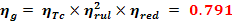
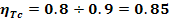
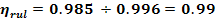
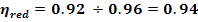
1.3Tip de motor (ASI 132M-38-8)
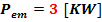
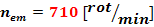
1.4 Stabilirea dimensiunilor electromotorului
A = 215 [mm] AA = 62 [mm] AB = 278[mm]
AC = 275 [mm] AD = 194 [mm] B = 178 [mm]
BA = 65 [mm] BB = 230 [mm] C = 89 [mm]
D = 38 [mm] E = 80 [mm] F = 10 [mm]
G = 33 [mm] GD = 8[mm] H = 132 [mm]
HA = 21 [mm] HC = 270 [mm] HD = 305 [mm]
K = 10 [mm] L = 490 [mm] KK = 2xIPE 16[mm]
LD = -
Curent nominal la 380 [V] = 8.35 [A]
Randament = 78%
Cosφ = 0.70
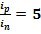
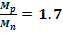
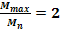
GD2 = 0.230 [Kgf ∙m2]
Masa neta = 71 [Kg]
1.5 Stabilirea rapoartelor
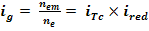
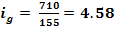
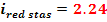
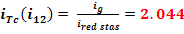
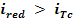
Cap.2 Proiectarea trasnsmisiei prin curele trapezoidale(inguste)
2.1 Date initiale
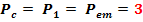

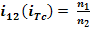
n2
= 
2.2 Tipul de curea (SPZ)
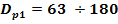
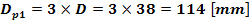
Dp2 = i12 Dp1 = [mm]
Dpm
= 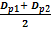
0.7(Dp1 + Dp2) ≤ A ≤ 2(Dp1 + Dp2)
266.35 ≤ A ≤ 761
A = 400 [mm]
2.3 Calculul parametrilor geometrici
γ - unghiul dintre ramurile curelei
γ
= 2arcsin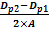
β - unghiul de infasurare pe roata
β1 = 180o - γ = 161.23o
β2 = 180o + γ = 198.77o
Lp - lungimea totala a curelei
Lp
= 2Asin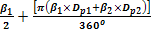
Lp stas = [mm]
A = [mm]
2.4 Calculul fortelor
v - viteza periferica
v
= 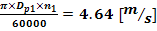
F - forta periferica
F
= 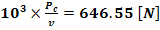
Fo - forta de intindere a curelei
Fo = (1.5 2)F = [N]
2.5 Calculul numarului de curele
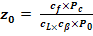
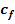
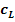
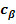
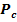
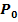
Cz - coeficient numar de curele = 0.95
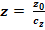
z0
= 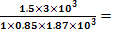
z = 2.98 ≈
2.6 Dimensiunile efective ale curelei
|
|
Tipul curelei |
Dimensiunile caracteristice ale sectiunii lp x h |
a [mm] |
H [mm] |
[mm] |
[o] |
Lungimi primitive Lp [mm] |
[mm] |
Sectiunea curelei Ac [mm] |
||
|
Min |
Max |
||||||||||
|
Curele trapezoidale inguste STAS 7192-65 |
SPZ |
8.5x8.0 |
|
| |||||||
Fig. 2.6 - Dimensiuni constructive curea trapezoidala
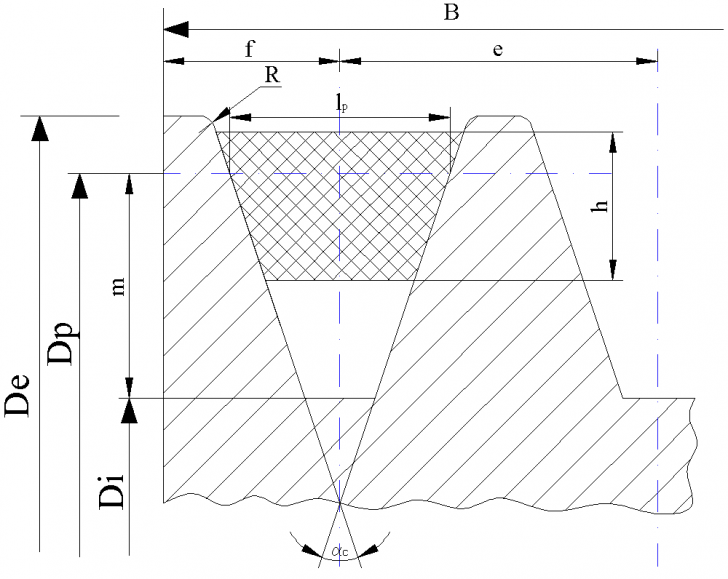
Fig. 2.7 a) - Dimensiuni constructive roata de curea trapezoidala
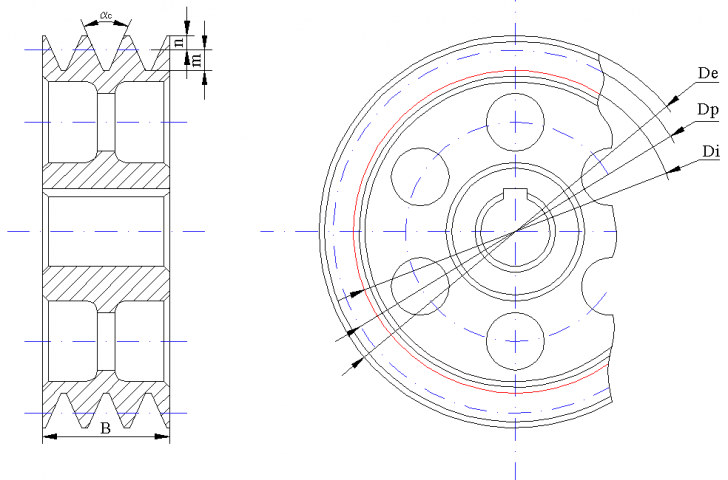
Fig. 2.7 b) - Reprezentare roata curea
Diametrul pimitiv minim Dp min = 80 [mm]
αc = 38o
Dimensiunile canalelor rotii de curea
lp = 8.5 [mm] f = 8 1 [mm]
nmin = 2.5 [mm] e = 12 0.3 [mm]
mmin = 9 [mm] r = 0.5 [mm]
h = 8 [mm]
CAP.3 Proiectarea angrenajelor cilindrice
cu dinti drepti
3.1 Date initiale
P1 = Pem ηTc
ηrul
P1 = 30.850.99 = [KW]
n1
= 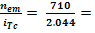
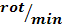
i12 = ired =
Predimensionarea angrenajelor cilindrice
In etapa de predimensionare , se determina distanta dintre axe din conditia de rezistenta a dintilor la oboseala de contact si modulul danturii din conditia de rezistenta a dintilor la incovoiere.
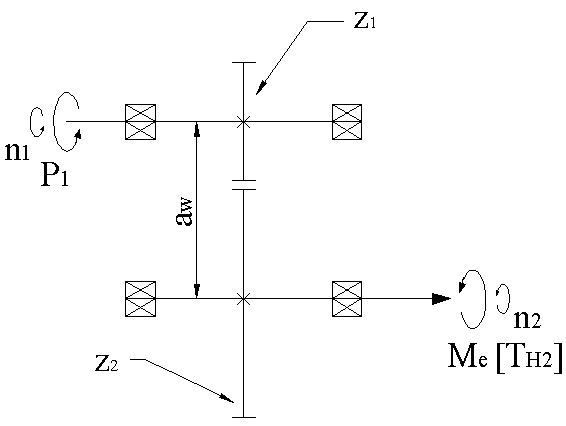
3.2.1 Distanta minima necesara dintre axe
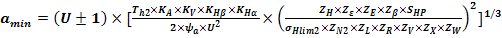
unde:
U
= i12 = ired = 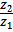
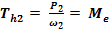
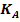
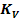
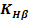
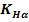
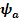
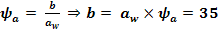
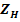
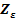
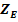
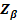
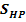
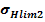
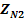
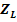
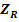
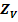
Fig. 3.2.1 - Distanta dintre axe
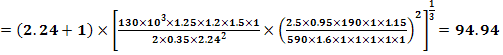
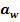
3.2.2 Modulul normal minim
necesar (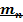
Modulul normal se calculeaza din conditia de rezistenta a dintilor la incovoiere.
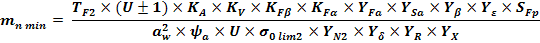
unde:
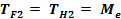
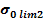
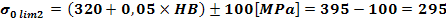
Duritatea materialului HB = 1400 2100 = 1500
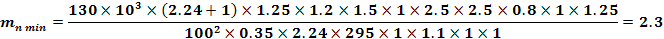
In continuare , modulul mn se stabileste dintre valorile de mai jos , in conformitate cu STAS 882 - 82
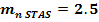
3.2.3 Stabilirea numarului de dinti
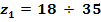
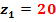
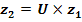
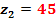
U
= 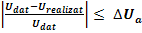
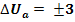
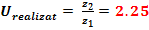
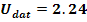
U
= 0.446 ≤ 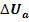
3.2.4 Recalcularea modulului normal
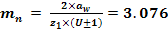

3.2.5 Distanta de referinta dintre axe
a
= 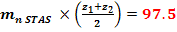
3.2.6 Unghiul de angrenare 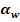
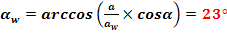
3.2.7 Suma deplasarilor 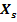
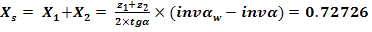
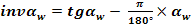
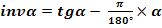
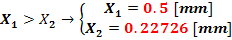
3.3 Calculul elementelor geometrice
3.3.1 Numarul de dinti al rotilor dintate cilindrice
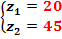
3.3.2 Modulul normal
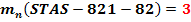
3.3.3 Calculul cremaluerei de referinta
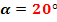
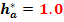
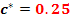
3.3.4 Raportul de transmisie
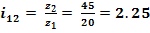
3.3.5 Elemente geometrice
Diametrul de divizare
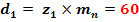
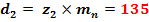
Diametrul de rostogolire
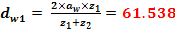
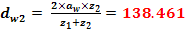
Coeficientul modificarii distantei dintre axe
Y
= 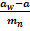
Coeficientul de miscare a jocului de referinta la cap
ΔY = Xs - Y = [mm]
Diametrul de picior
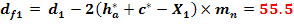
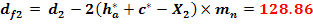
Inaltimea de referinta
h
= 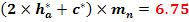
Diametrul de cap scurtat daca e cazul
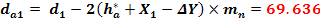
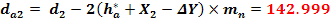
Diametrul de baza
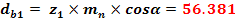
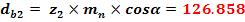
Pasul de divizare
P = πmn = 9.424
Pasul de rostogolire
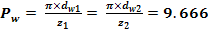
Pasul de baza
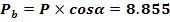
Unghiul de presiune la capul dintelui
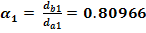
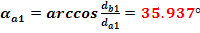
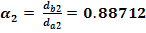
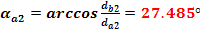
Gradul de acoperire al angrenajului
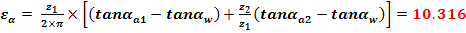
3.3.6 Calculul dimensiunilor de masurare
Unghiul
de presiunepe cilindrul de diametru 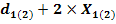
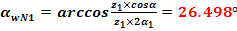
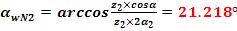
Numarul teoretic de dinti pentru cota peste dinti
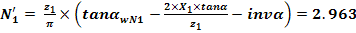
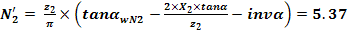
Numarul real (adoptat) de dinti pentru masurarea cotei peste dinti
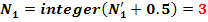
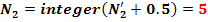
Lungimea (cota) peste N dinti
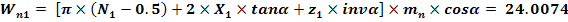
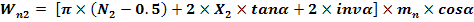
3.3.7 Stabilirea latimii danturii
b = ψaw = 0.35100 = 35 [mm]
CAP.4 Proiectarea arborilor
Predimensionarea urmareste determinarea dimensiunilor arborilor. Conditiile constructive impun distanta dintre reazeme si pozitia reactiunilor unde actioneaza sarcinile exterioare.
4.1 Alegerea materialului
Pentru arbori alegem materialul OLC45
σIII = 55 [MPa]
σII = 95 [MPa]
4.2 Predimensionarea arborilor
Se face din conditia de rezistenta la torsiune (arborele 1)
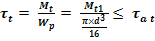
rezistenta
admisibila la torsiune - 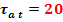
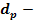
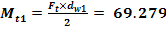
Mt
2 = 
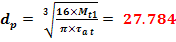
4.3 Stabilirea dimensiunilor treptelor arborelui (diametre si lungimi)
Lungimile butucilor pe care se monteaza rotile dintate si roata de curea
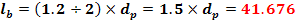
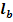
Lungimile fusurilor de lagare si de rulmenti
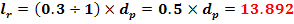
Lungimile
tronsoanelor care separa organe afate in miscare relative in interiorul
carcasei 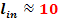
Lungimile tronsoanelor care separa organe afate in miscare relative in afara carcasei
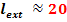
Lungimile tronsoanelor pe care se face
etansarea 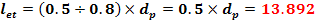
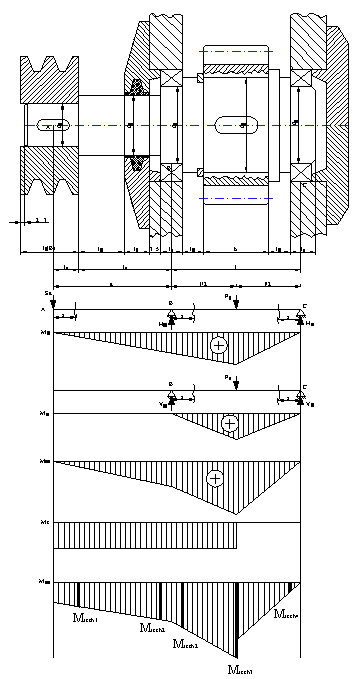
Fig. 4 - Diagramele de solicitare ale arborelui
4.4 Lungimile treptelor Se stabilesc in functie de schema de montaj
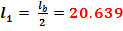
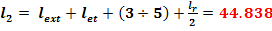
a = 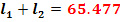
l = b + 2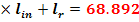
4.5 Calculul reactiunilor Se tine cont de fortele de incarcare
Forta de incarcare a arborelui de curea 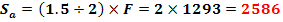
Forta
tangential din angrenaj 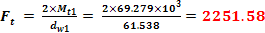
Forta radiala din angrenaj 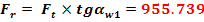
Acriunea sarcinilor se studiaza in doua plane : orizontal shi vertical
Planul orizontal (H)
Ecuatia de forte
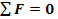
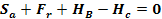
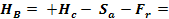
Ecuatia de momente
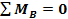
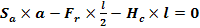
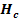
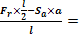
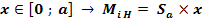
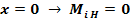
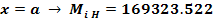
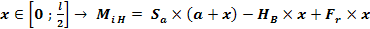
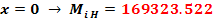
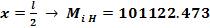
Planul vertical (V)
Ecuatia de forte
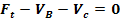
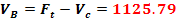
Ecuatia de momente
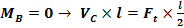
Vc = 1125.79 [N]
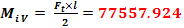
4.6 Calculul momentului de incovoiere rezultant si trasarea diagramei (Fig.4)
Se face in doua plane :
in planul punctului B
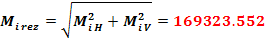
la mijlocul distantei dintre B si C
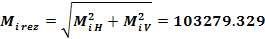
4.7 Trasarea diagramei momentului de torsiune
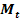
Se realizeaza de la intrare pana la punctual de mijloc al danturii rotii dintate cilindrice pentri arborele 1(Fig. 4)
4.8 Determinarea momentului incovoietor echivalent in sectiunile necesare
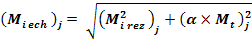
j = (15)
Coeficientul α pentru ciclul de solicitare alternant simetric
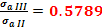
4.9 Calculul diametrului pentru fiecare tronson al arborelui

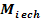
|
Nr. crt. |
[N∙mm] |
[N∙mm] |
[mm] |
|
Arbore 1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nr. crt. |
[Nmm] |
[Nmm] |
[mm] |
[mm] |
|
Arbore 1 |
||||
Bibliografie
1. M. Gafitanu - Indrumar proiectarea organelor
de masini. Curele si lanturi. Institutul Politehnic
2. M. Gafitanu - Indrumar de proiectare arbori
drepti, imbinari cu pene si caneluri, lagare radiale. Institutul Politehnic
3. Liviu Hostiuc - Reductoare cu roti dintate.
Institutul Politehnic
4. M. Gafitanu - Organe de masini vol. I. Editura tehnica, Bucuresti, 1980;
5. M. Gafitanu - Organe de masini vol. II. Editura tehnica, Bucuresti, 1981.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3540
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved