DEPENDENTE FUNCTIONALE

Introducere

Cand descriem un univers real sau conceptual printr-un model relational ne confruntam cu urmatoarea problema:

Care este multimea de relatii care va fi o reprezentare fidela a schemei conceptuale ( a obiectivelor si a legaturilor) si deci a universului real fara ca sa riscam problemele de cosistenta (la operatiile de actualizare sau operatiile de descompunere). Plecand de la regulile semantice care traduc restrictiile universului modelat, proiectantul trebuie sa defineasca "dependentele " si sa le introduca in definitia schemei de relatie. Proprietatile dependentelor sunt proprietati pentru schema de relatie (intensiuni) a bazei de date si nu pentru o extensie oarecare, adica aceste dependente constituie invarianti care trebuie sa fie satisfacute de toate extensiile legale de relatii ale schemei.

Crearea unei baze de date are doua obiective esentiale : sa reduca excedentul de date si sa mareasca siguranta in exploatare. Orice cunostinta apriori despre diferite tipuri de restrictii referitoare la totalitatea datelor poate fi de mare folos pentru atingerea acestor obiective.

Un procedeu de formalizare a unor cunostinte despre date este dat de dependente. In acest paragraf vom considera numai un singur tip de dependente si anume dependenta functionala, pe care o vom numi F- dependenta. Dependenta functionala este o generalizare a notiunii de cheie.

Exemplul 1. Fie relatia grafic( PILOT CURSA DATA ORA‑DECOLARE ) care arata ce pilot participa la o cursa data, la o anumita data si ora la care are loc decolarea (fig. 1). Se au in vedere urmatoarele restrictii:

o cursa are aceeasi ora de decolare ( de exemplu cursa 75 decoleaza intotdeauna la ora

10:15 ).

un pilot nu se poate afla decat intr‑o singura cursa la o anumita ora de decolare.

Aceste restrictii sunt exemple de F- dependente. Intuitiv vorbind, o F- dependenta are loc cand valorile tuplurilor dupa o multime de atribute definesc in mod unic valorile unei alte multimi de atribute. Astfel, restrictiile aratate mai sus pot fi astfel formulate:

‑ ORA‑DECOLARE depinde functional de CURSA

- CURSA depinde functional de

- PILOT depinde functional de

In mod obisnuit, ordinea acestor secvente se poate schimba si spunem ca,

defineste in mod functional pe , sau simbolic

.

Vom da o definitie stricta a dependentei functionale folosind operatorii relationali.

grafic(PILOT CURS DATA ORA‑DECOLARE )

Dragos 75 9‑03 10:15

Dragos 80 13:25

Mihai 80 8‑03 13:25

Mihai  80 12‑03 18:50

Mihai  75 11‑03 10:15

Mircea 75 13‑03 10:15

Mircea 80 12‑03 13:25

Costin 85 9‑03 5:50

Costin 85 13‑03 5:50

Costin 90 5‑03 13:25

__________ ______ ____ ____________________

Figura 1.Relatia grafic

Definitia 1. Fie relatia r de schema R, X si Y submultimi ale lui R. Relatia r satisface dependenta functionala X Y daca p_Y s_X=x(r)) are nu mai mult de o singura ocurenta pentru fiecare X‑valoare x.

In F- dependenta X Y submultimea X se numeste partea stanga iar Y se numeste partea dreapta.

Un procedeu de a verifica ca o relatie satisface X Y este dat de urmatoarea proprietate :

Daca pentu orice doua tupluri t₁,t_{2 I}r, cu t₁(X) = t₂(X) rezulta t₁(Y)=t₂(Y) atunci r satisface X Y.

Aceasta caracterizare sta la baza procedurii satisfie data mai jos. Presupunem ca relatia r este ordonata dupa valorile lui X, apoi dupa ale lui Y.

0 procedure satisfie(X,Y;v)

1 v true

2 Input (t)

3 While not eof (r)

3.1 Input

3.2 If t(X) = t'(X)

Then

3.2.1 If t(Y) t'(Y)

Then

3.2.1.1 v False

3.2.2 continue

Else

3.2.3 t t'

3.3 Continue

4 Return

Tabelul de mai jos arata rezultatul aplicarii algoritmului satisfies relatiei grafic.

grafic( PILOT CURSA DATA ORA‑DECOLARE )

Dragos 75 9‑03 10:15

Mihai 75 1‑03 10:15

Mircea 75 3‑03 10:15

‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑

Dragos 80 10‑03 13:25

Mircea 80 12‑03 13:25

‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑

Mihai 85 8‑03 5:50

Costin 85 9‑03 5:50

Costin 85 13‑03 5:50

‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑

Mihai  87 12‑03 18:50

Costin 90 15‑03 13:25

Rezultatul aplicarii algoritmului satisfie este True.

Axiome de inferenta

Pentru orice relatie r(R) exista la un moment dat o familie de F- dependente pe care le satisface r. Trebuie remarcat ca, o stare a unei relatii poate satisface o multime anumita de F- dependente iar o alta stare poate sa nu o satisfaca.

Trebuie sa determinam familia F de F- dependente care satisface toate starile admisibile ale relatiei. Pentru a determina F sunt necesare cunostinte semantice despre relatia r. De aceea trebuie sa consideram ca familia F de F- dependente este data pentru schema de relatie R. In acest caz orice relatie r(R) trebuie sa satisfaca toate F- dependentele din F. Nu este evident care dintre afirmatiile urmatoare este mai importanta :

- care este multimea de stari admisibile ale unei relatii r care defineste o F- dependenta,

‑ care F- dependente determina restrictiile impuse schemei de relatie R.

Numarul de F- dependente care pot fi aplicate unei relatii este finit, deoarece exista numai un numar finit de submultimi ale lui R. Prin urmare intotdeauna se poate determina toate F- dependentele pe care le poate satisface o relatie r prin triere cu ajutorul procedurii satisfie.

Totusi acest procedeu necesita mult timp deoarece trebuie generate si apoi testate toate submultimile schemei R. Daca insa sunt cunoscute cateva F- dependente din F atunci adesea se pot gasi cele ramase.

O multime de F- dependente F implica F- dependenta X Y (notata F╞═X Y ) daca orice relatie care satisface F satisface X Y.

Definitia 2. O inferenta este o regula care arata ca, daca o relatie care satisface un grup de F- dependente atunci ea satisface de asemenea un alt grup.

Vom introduce sase axiome de inferenta pentru dependente functionale in formularea axiomelor se folosesc urmatoarele notatii :

‑ r ‑ pentru relatii si

‑ X, Y, Z,W ‑ pentru submultimi ale lui R.

Axioma I ( Reflexivitate ): Relatia p_X s_{X x}(r)) are cel mult un tuplu pentru orice X‑valoare x, prin urmare are loc X X.

Axioma II ne da posibilitatea sa extindem partea din stanga a unei F- dependente X Y.

Axioma II ( Augmentare ): Dacap_Y s_{X x}(r)) are cel mult un tuplu pentru orice X‑valoare x si Z este o submultime oarecare a lui R atunci : p_Y s_{XZ xz}(r)) are nu mai mult de un tuplu si prin urmare : XZ Y.

Exemplul 2. Se considera relatia r data in continuare care satisface F- dependenta A B

r(A B C D )

a₁ b₁ c₁ d₁

a₂ b₂ c₁ d₁

a₁ b₁ c₁ d₂

a₃ b₃ c₂ d₃

si prin urmare rezulta ca sunt adevarate urmatoarele F- dependente :AB B, AC B, D B,

ACD B, ABCD B

Axioma III ( Aditivitate ): Aceasta axioma ne permite sa unim doua F- dependente care au partea stanga aceeasi. Daca relatia r satisface F- dependentele X Y si X Z atunci ambele proiectii p_Y s_{X x}(r)) si p_Z s_{X x}(r)) au cel mult un tuplu pentru orice X‑valoare x. Daca p_YZ s_{X x}(r)) ar avea mai mult de un tuplu atunci cel putin una din relatiile p_Y s_{X x}(r)) si p_Z s_{X x}(r)) ar avea mai mult de un tuplu penntru orice X-valoare x. Prin urmare X YZ.

Exemplul 3. Fie relatia r din exemplul 1 care satisface F- dependenta A C atunci din axioma din A3 rezulta ca r satisface A BC.

Axioma IV ( Proiectivitate ): Daca r satisface X YZ, atunci p_YZp_Y s_{X x}(r)) are cel mult un singur tuplu pentru orice X‑valoare x. Atunci p_Y p_YZ s_{X x}(r)))= p_Y s_{X x}(r)) are cel mult un tuplu, prin urmare r satisface X Y.

Exemplul Relatia din exemplul 2 satisface relatia A BC. Conform axiomei IV r satisface relatiile A B si A C.

Axioma V ( Tranzitivitate ): Fie relatia r care satisface F- dependentele X Y si Y Z. Sa consideram tuplurile t₁ si t₂ din r. Daca t₁(X)= t₂(X) atunci t₁(Y)= t₂(Y) din care rezulta t₁(Z)= t₂(Z) deci X Y.

Exemplul 5. Relatia r data mai jos satisface F- dependentele A B si B C. Din axioma V rezulta ca r satisface A C.

r( A B C D )

a₁ b₁ c₂ d₁

a₂ b₂ c₁ d₂

a₃ b₁ c₂ d₁

a₄ b₁ c₂ d₃

Axioma VI ( Pseudotranzitivitate ): Fie relatia r care satisface F- dependentele X Y si YZ W, si doua tupluri t₁ si t₂ din r. Din conditia t₁(X)= t₂(X) rezulta t₁(Y)= t₂(Y) si analog din t₁(ZY)= t₂(YZ) rezulta t₁(W)= t₂(W). Din t₁(XZ)= t₂(XZ) rezulta t₁(X)= t₂(X) ceea ce implica t₁(Y)= t₂(Y) si t₁(YZ)= t₂(YZ) de unde rezulta t₁(W)= t₂(W). Prin urmare YZ W.

Prin urmare, daca X,Y,Z si, W sunt submultimi ale lui R atunci pentru orice relatie r de schema R sunt adevarate urmatoarele axiome de inferenta:

A1. Reflexivitate: X X

A2. Augmentare: X Y T XZ Y

A3. Aditivitate : X Y si X Z T X YZ,

A Proiectie: X YZ T X Y si X Z

A5. Tranzitivitate: X Y,Y Z T X Z

A6. Pseudotranzitivitate: X Y, YZ W T XZ W.

Folosind axiomele A1-A6 se poate obtine alte F- dependente.

Exemplul 6. Fie relatia r de schema R si X,Y R din axioma A1 rezulta Y Y, aplicand axioma A2 obtinem XY Y. Din proiectie rezulta ca daca Y X R atunci X Y pentru orice relatie.

Exemplul 7. Fie relatia r de schema R si X,Y,Z R. Presupunem ca r satisface F -dependentele X Y si XY Z atunci din axioma A6 rezulta ca XX Z adica X Z.

Exemplul 8. Pentru a nega o afirmatie referitoare la o F- dependenta este suficient sa aratam ca, exista cel putin o relatie care nu satisface aceasta inferenta. Daca negam afirmatia, ca din

XY WZ rezulta X Z dam contraexemplul dat de relatia r care satisface AB CD dar nu pe

A C

r(A B C D)

a₁ b₁ c₁ d₁

a₂ b₂ c₂ d₁

Anumite axiome pot fi deduse unele din altele. De exemplu tranzitivitatea rezulta din axioma A6 luand Z= . Axioma de pseudotranzitivitate rezulta din axiomele A1, A2, A3 si A5,

1 X Y (data)

2 YZ W (data)

3 Z Z ( A1 )

4 XZ Z (A2 la 3)

5 XZ Y ( A2 la 1)

6 XZ YZ (A3 la 3 si 4)

7 XZ W (A5 la 2 si 6).

In paragraful urmator vom arata ca sistemul de axiome A1-A6 este complet, adica orice F- dependenta implicata de F poate fi obtinuta prin aplicarea de un numar finit de ori a axiomelor A1-A6 unor F- dependete din F.

Exercitiu: Demomnstrati ca, din A1, A2, A6 se deduc A2, A4 si A5.

. Completitudinea sistemului de axiome

Fie F o multime de F- dependente pentru relatia r de schema R.

Definitia 3. Se numeste inchidere a lui F, notata F⁺, cea mai mica multime de F- dependente pe R care contine F si orice aplicare a axiomelor A1-A6 la elementele ei, nu mai genereaza o alta F- dependenta care sa nu o contina.

Deoarece F⁺ este finita o putem calcula plecand de la , prin aplicarea axiomelor A2, A2, A6 pana nu mai rezulta nici o noua F- dependenta. Inchiderea lui F depinde de schema R, de exemplu daca R=AB atunci F⁺ va contine pe B B dar nu si pe C C. Cand schema R nu este definita explicit se presupune ca este formata din multimea tuturor atributelor utilizate in dependentele care compun pe F.

Definitia O F- dependenta X Y este derivata din F daca X YIF⁺ (sau ca F determina pe X Y)

Definitia 5. Spunem ca F implica X Y daca orice relatie care satisface F atunci satisface X Y.

Deoarece axiomele de inferenta sunt adevarate si daca F determina X Y atunci F implica X Y.

In continuare vom arata ca axiomele ca A1-A6 ne permit sa deducem toate F-dependentele implicate de F. Pentru a demonstra acest rezultat va trebui sa aratam cum se construieste pentru F o relatie care satisface F⁺ si nici o alta relatie in plus.

Definitia 6. Spunem ca X Y este o F- dependenta pe R daca X,Y R. F este o multime de F- dependente pe R daca pentru orice F- dependenta X Y din F atunci X,Y R.

Definitia 7. Daca F este o multime de F- dependente pe R si G multimea tuturor F- dependentelor posibile pe R, atunci se numeste exterior a multimi F, multimea F^- =G-F⁺.

F-depenedenta X Y pe R se numeste triviala daca X Y. Orice relatie r(R) satisface dependenta triviala X Y. Daca F este o multime de F-dependente pe R si X este o submultime a lui R atunci exista o F- dependenta X Y in F⁺ astfel incat Y sa fie maximala. Pentru orice alta F-dependenta X Z din F⁺ rezulta ca Z Y. Acest rezultat se numeste inchiderea lui X in raport cu F, se noteaza cu X⁺ si contine intodeauna pe X.

Exercitiu. Fie F=calculati inchiderea lui F.

Exemplul 9. Fie F= atunci AB⁺= ABCDEH.

Torema 1. (completitudine) Sistemul de axiome A1-A6 este complet. Adica F╞═X Y X YIF⁺.

Demonstratie. Fie F o multime de F-dependente pe R. Pentru orice X YI F^- vom determina o relatie r(R) care satisface F⁺ dar nu pe X Y. Prin urmare nu exista F-depenednta inplicata de F care sa nu fie derivata din F. Fie schema R= A₁A₂A_n si a_i,b_i elemente distincte din dom(A_i), 1 i n si relatia r formata din doua tupluri t si t'. Tuplul t=< a₁, a₂, .,a_n> iar tuplul t' este definit de

a_i daca A_iIX⁺

t'=

b_i daca A_i X⁺

Mai intai vom arata ca r nu satisfce X Y. Din definitia lui r rezulta ca t(X)=t'(X). Presupunem prin absurd ca t(Y)=t'(Y). Atunci t'(Y) are numai componente a_i si prin urmare Y .X⁺. Dar

X X⁺ si din proiectivitate rezulta ca X⁺ Y si din tranzitivitate rezulta ca X YIF⁺ contradictie cu faptul ca X YIF-.

Vom arata ca r satisface toate F-dependentele din F⁺. Va trebui sa consideram numai acele F- dependente W Z in care W X⁺. Din proiectivitate rezulta ca X⁺ W si din tranzitivitate rezulta ca X⁺ Z prin urmare X⁺ Z si deci t(Z)=t'(Z) deci r satisface F⁺.

Corolar 1. Pentru orice multime de F- dependente F pe schema R exista o relatie

r( R) care satisface F⁺ dar nu satisface F^-.

r = r_xy

X YIF^-

Relatia r_xy formata numai din cele doua tupluri se numeste relatia lui Armstrong.

Pentru orice F-dependenta X Y din F folosind teorema 1 construim relatia r_xy(R) care satisface F⁺ dar nu pe X Y. Schimbam intrarea in fiecare relatie, astfel incat aceasta sa nu fie comuna pentru nici o relatie

r = r_xy

X YIF-

Este evident ca r nu satisface nicio F- dependenta din F-. Din teorema 1 rezulta ca r satisface F⁺. Deci sistemul de inferente este complet si necontradictoriu. Pentru calculul inchiderii lui F se foloseste sistemul de axiome A1-A6 dat de Armstrong sau orice alt sistem complet de axiome.

Pentru a verifica ca multimea de F- dependente F╞═X Y va trebui sa verificam daca X YIF⁺. Aceasta varianta dureaza foarte mult. Este de dorit un procedeu de verificare a apartenentei lui X Y la F⁺ fara a genera toate dependentele care o compun. Nucleul algoritmului il reprezinta o procedura de calcul a inchiderii lui X in raport cu F. Dupa ce s-a calculat X⁺ se verifica daca F╞═X Y. Procedura closure data mai jos returneaza X⁺ in raport cu F.

PROCEDURE Closure(X,F;X⁺)

DV

DN X

WHILE DV DN

3.1 DV DN

3.2 FOR fiecare W ZIF

IF DN W

THEN

. 1 DN DN Z

CONTINUE

3.3 CONTINUE

X⁺ DN

RETURN

Procedura closure este utilizata in functia termen de testare a apartenentei lui X Y la F⁺.

FUNCTION termen(F, X Y)

CALL closure(X,F;X⁺)

IF Y X⁺

THEN

2.1 termen true

ELSE

2.2 termen false

RETURN

Secvente derivate

Daca F╞═ X Y atunci X Y fie este continuta in F, fie poate fi obtinuta prin aplicarea unei secvente de inferente la anumite F- dependente din F. Aceasta secventa de aplicare a axiomelor si a F- dependentelor rezultate se numeste derivata lui X Y din F.

Definitia 8. O secventa P de F- dependente pe R este derivata din F, daca orice F- dependenta din P este fie un termen din F, fie este rezultata din F-dependentele care o preced in secventa prin aplicarea uneia dintre axiomele de la A1 la A6.

Definitia 9. Se numeste derivta a F- dependentei X Y din F o secventa de F- dependente derivate din F care o contin.

Deci F ╞═ X Y daca exista o derivata din F care o contine.

Exemplul 10. Fie F =. Urmatoarea secventa este o derivata a lui AB DK:

1. AB C (data)

2. C D ( data)

3. AB D (tranzitivitate din 1 si 2)

B B ( reflexivitate)

5. AB B (augmentare din 4)

6. AB BC (trazitivitate din 4 si 5)

7. BC E (data)

8. AB E (tranzitivitate din 6 si 7)

9. AB DE (aditivitate din 6 si 8)

10. DE K (data)

11. AB K (tranzitivitate din 9 si 10)

AB DK (aditivitate din 3 si 11 )

AB BE (aditivitate din 1 si 8)

In continuare se foloseste o alta multime completa de inferente care nu este o submultime a lui A1A6 unde inferentele sunt numite B_axiome. Fie r(R) si submultimile X,Y,Z,W ale schemei R si un atribut A din R Vom arata apoi ca axiomele lui Armstrong A1,A2,A6 se deduc din B_axiomele B1, B2,B3 :

B1. Reflexivitatea : X X,

B2. Acumularea : X YZ, Z AW T X AYZ,

B3. Proiectie : X YZ T X Z sau X Y.

A1. Reflexivitatea, aceeasi cu B1.

A2. Augmentarea :

1: XZ XZ (B1)

2: X Y=A₁ A₂. .A_n (data)

3: X XYZ  (aplicam de n ori B2 la 1 si 2)

4: XZ Y (aplicam B3 la 3)

A6. Pseudotrazitivitate :

1. XZ XZ  (B1)

2. X Y=A1A2..Am  (data)

3. XZ XYZ  (aplicam de m ori B2 la 1 si 2)

YZ W= C1C2..Ck (data)

XZ XYZW (aplicam de k ori B2 la 3 si 4)

X Z   (aplicam B3 la 5)

Deoarece sistemul de B‑axiome este complet intotdeauna se poate gasi o derivata care sa utilizeze numai B1, B2, B3 daca F ╞═X Y.

Exemplul 11. Fie F multimea din exemplul 10. Atunci :

1. CE CE (reflexivitate)

2. C D  (data)

3. CE CDE (acumulare din 1 si 2)

CE DE (proiectivitate din 3)

5. DE K  (data)

6. DE DEK (acumulare din 4 si 5)

AB AB (reflexivitate)

8. AB C  (data)

9. AB ABC (acumulare 7 si8)

10. BC E  (data)

11. AB ABCE (acumulare din 10 si 11)

12. AB ABCDE (acumulare din 4 si 12)

13. AB ABCDEK (acumulare din 5 si 12)

1 AB DK  (proiectivitate din 13)

este o derivata pentru care se utilizeaza numai B‑axiome.

5. RAP‑secvente de derivate

Definitia 10. Se numeste derivata RAP din F a F- dependentei X Y o secventa obtinuta prin aplicarea B‑axiomelor si care satisface urmatoarele conditii:

i. Prima F-dependenta este X X;

ii.          Ultima F-dependenta este X Y

iii.        Orice F-dependenta din secventa diferita de prima si ultima, fie apartine lui F, fie are forma X Z si este obtinuta prin aplicarea axiomei B2.

Exemplul 12.

1. AB AB (B1)

2. AB C (data)

3. AB ABC (B2 la 1 si 2)

C D  (data)

5. AB ABCD (B2 la 3 si 4)

6. AD E (data)

7. AB ABCDE (B2 la 5 si 5)

8. DE K  (data)

9. AB ABCDEK (B2 la 7 si 8)

10. AB DK  (B3)

este o RAP‑secventa derivata a lui AB DK din F.

Teorema 2. Fie F o multime de F- dependente pe R. Daca exista o secventa derivata a lui X Y din F atunci exista o RAP‑secventa de derivata a lui X Y din F.

Demonstratie. Fie P o secventa derivata din F a lui X Y, care foloseste B‑axiomele B2,B3. Eliminam din P toate F-dependentele care sunt dupa prima aparitie a lui X Y. Daca prima F-dependenta din P nu este X X atunci o adaugam la inceputul secventei. Mai departe aratam ca se pot obtine F-dependente in P fara a folosi F- dependente formate cu ajutorul axiomei B3. Fie o F-dependenta Z W din P diferita de ultima dedusa din Z WV cu ajutorul axiomei B3. Daca F-dependenta nu se foloseste mai departe in deducerea nici unei F-dependente din P atunci aceasta se elimina din P.

Daca in continuare este folosita pentru determinarea unei F-dependente din P atunci trebuie sa fie utilizta in una din axiomele B2 sau B3. Daca F-dependenta este utilizata intr‑o axioma B3 atunci din ea trebuie sa se obtina X W si atunci ea poate fi eliminata din P.

Daca la Z W se aplica B2 atunci trebuie sa existe doua cai :

1. W W Z W, Z W, W' AU T Z AW

2. Z Z", U Z", Z BW T U BZ", BIW

In primul caz,   punem Z W in locul Z AW. In al doilea caz punem Z VW in locul lui ZW. In toate cazurile o eliminam din P. Deja am aratat, ca se poate inlocui cu o F- dependenta cu partea dreapta cea mai mare intr‑o secventa de derivare dedusa numai prin axiomele B1‑B3. Unicitatea rezultatului este dat de posibilitatea reprezentarii printr‑o F- dependenta cu partea dreapta mai mare decat F-dependenta obtinuta initial. Acum P are urmatoarea forma, incepe cu X X se termina cu X Y si nu contine nici o dependenta dedusa cu ajutorul axiomei B3 excluzand ultima. Prin urmare, F-dependenta cu partea dreapta cea mai mare poate sa inlocuiasca intreaga secventa de inferente P. Dependenta X Y poate fi dedusa din ultima cu ajutorul lui B3.

6. Grafuri aciclice orientate derivate (DAG)

Definitia 11. Un graf aciclic orientat este un graf orientat care nu are cicluri in nici un virf.

Definitia 12. Fie F o multime de F-dependente in raport cu schema R. Se numeste graf aciclic orientat derivat din F un graf aciclic orientat ale carui noduri sunt atribute din R si construit dupa urmatoarele reguli :

R1. Orice multime arbitrara de noduri izolate notate cu simboluri din R este un graf aciclic orientat de inferenta.

R2. Fie H un graf aciclic orientat derivat din F care contine nodurile n n n_k etichetate cu A₁, A₂,. .A_k si F-dependenta A₁A₂..A_k CX in F. Construim H' adaugand la H nodul u notat cu C si arcele (n .u) (n .u). . (n_k,u) atunci H' este un graf aciclic orientat derivat din F.

R3. Niciun alt garf nu este graf aciclic orientat de inferente pe F.

Definitia 13. Daca H este un graf aciclic orientat derivat din F, nodul este initial daca in el nu intra niciun arc. Orice nod initial il adaugam la H cu ajutorul regulii R1.

Definitia 1 Fie H un graf aciclic orientat derivat din F. Graful H se numeste graf aciclic orientat pentru X Y, daca :

D1: X este o multime de noduri initiale;

D2: Fiecare atribut din Y este un nod oarecare al unui varf din H.

Definitia 15. Se numeste multime utila a grafului aciclic orientat derivat din F, notata U(H), multimea tuturor F-dependentelor din F utilizate de regula R2 la construirea grafului aciclic orientat derivat.

Exemplul 1: Fie F = dam mai jos etapele de construire ale grafului aciclic orientat derivat din F :

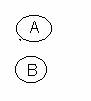
a) Regula R1 

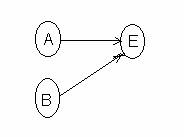
b) Aplicarea regulii R2 AB E

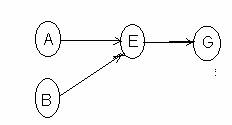
c) Aplicarea regulii R2 E G

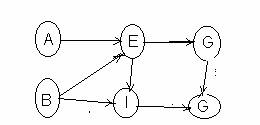
d) Aplicarea regulii R2 BE I si GI H

Exemplul 13. Graful din figura 1 este un graf aciclic orientat derivat din F pentru AB DE. Multimea utila este . Nodurile initiale sunt notate cu A si B.

Observatie : Fie H un graf aciclic orientat derivat din F, cu multimea nodurilor initiale notate cu literele care compun multimea atributelor X, iar varfurile ramase cu litere din multimea Y. Daca Y' este o submultime a lui Y, atunci H este un graf aciclic orientat derivat din F pentru X Y".

Teorema 3. Fie o multime de F-dependente F in raport cu schema R si F- dependenta X Y, urmatoarele afirmatii sunt echivalente :

1. F╞═ X Y.

2. Exista o secventa de inferente pe F pentru X Y.

3. Exista un graf aciclic derivat din F pentru X Y

Demonstratie. Dupa cum se observa din teorema de completitudine rezulta echivalenta afirmatiilor 1 si 2. Din teorema 2, aplicata afirmatiei 2, rezulta ca exista o RAP‑secventa de inferente pentru X Y dedusa din F. Aratam ca se poate construi un graf aciclic orientat derivat din F pentru X Y. Axioma B2 corespunde regulii R2. Axioma B3 este continuta in conditia R2 definita de graful aciclic orientat derivat din F pentru X Y.

Fie P o RAP‑secventa de inferente pentru X Y pe F. Pentru ca sa avem X in partea stanga admitem ca toate F-dependentele din F au aceiasi parte X : 

Demonstram prin inductie, ca se poate construi secventa H₁,H₂,,H_k de grafuri aciclice orientate derivate din F, astfel ca H_i se obtine din H_{i_1} cu ajutorul regulilor de constructie ale grafurilor aciclice orientate derivate si H_i este DA‑graf pentru X Z_i

Desigur, ca X Z₁ trebuie sa fie X X. Pentru construirea DA‑grafului H₁ care consta din varfuri izolate fara legaturi ale carui noduri sunt atributele din X folosim regula R1. Presupunem ca H₁,H₂,,H_i-1 sunt DA‑grafuri pentru X Z₁,. ,X Z_i-1. Consideram X Z_i. Aceasta F- dependenta poate fi obtinuta prin unul din cele trei procedee.

1. Direct din F.

2. Din F-dependentele X Zi si X Z_i sI Z CW cu ajutorul axiomei B2. In acest caz j<i, Z CW apartin lui F, Z_j contine Z si Z_i=CZ_j.

3. Din F-dependentele X Z_j cu ajutorul axiomei B3. In acest caz j<i, Z_j contine Z_i si Z_i=Y.

In cazul 1 punem Z_i=B₁B₂..B_m. Atunci DAG-ul H_{i_1} contine DA‑graful H_i si aplicand regula R2 la H_{i_1} pentru fiecare atribut din Z_i, adaugam virfurile notate cu B₁B₂..B_m si arcele care intra in aceste varfuri plecand din atributele lui X.

Ca rezultat se obtine H_i iar H_j contine varfurile marcate prin atributele din Z_j. Ca sa obtinem H_i adaugam la H_{i_1} virful marcat cu c, ce este folosit in regula R2.

In cazul 3, H_j este deja un DAG pentru X Z_i deoarece H_{i_1} contine H_j, atunci si H_{i_1} este un DAG. Punem H_i=H_{i_1}. Dupa terminarea construirii tuturor DAG-urilor H_i graful H_k va fi un DAG pe F pentru X Y. Fie H un graf aciclic orientat derivat din F pentruX Y. Construim RAP‑secventa de inferente din H. Vom presupune ca este o secventa de DAG-uri pe F, astfel cat H_i este construit din H_{i_1} cu ajutorul regulii R2, 2<j<k si H_k=H.

Fie Z_i multimea care marcheaza nodurile in H_i. Construim RAP‑secventa de inferente P din F pentu X Y dedusa din H prin X Z₁X Z_k. Presupunem dat sirul H₁H₂..H_k de DAG uri pe F. Multimea Z₁ trebuie sa fie X, iar H₁ trebuie sa fie un DAG cu varfurile izolate cu atribute din X.

Fie P care incepe cu X X. Acum consideram H_i pentru i>1. H_i se obtine din H_{i_1} cu ajutorul regulii R2 prin folosirea F- dependentei Z CW din F, unde C este un nod marcat, adaugand la H_{i_1}, pe Z_{i_1} care contine Z. Prin urmare Z_i=CZ_i-1. Daca Z CW nu apartine lui P, atunci o adaugam P. Apoi X Zi adaugam la sfarsitul lui P . Dependenta X Z_i se poate obtine cu ajutorul axiomelor X Z_i-1 si Z CW.

La terminarea acestui proces obtinem RAP‑secventa de inferente pentru X Z_k unde Z_k contine Y. Adaugam X Y la sfarsitul lui P folosind axioma B3. Acum P este RAP‑secventa de inferente pentru X Y.

Corolar 2. Exista un graf aciclic orientat derivat din F pentru cu U(H)=G daca si numai daca exista o RAP‑secventa de inferente pe F pentru cu multimea utila G.

Exemplul 14 : Secventa a DAG din 6.1 poate fi reprezentata prin RAP‑secventa de inferente:

1. AB AB

2. AC C

3. AB ABC

C D

5. AB ABCD

6. BC I

7. AB ABCDI

8. I E

9. AB ABCDEI

10.AB DE

Axioma B2 si regula R2 pot fi deduse una din alta prin acelasi procedeu. Varianta tare a lui B2 poate fi reprezentata in forma :

B2 : X YZ, Z VW TX YZV

unde V este o submultime a multimii R.

Lema 1. Daca exista un graf aciclic orientat derivat din F pentru X Y atunci exista un graf aciclic orientat derivat din F ale carui noduri sunt formate din atribute distincte.

Demonstratie Vezi Maier/ /.

Lema 2. Fie H un graf aciclic orientat derivat din F pentru X Y iar V W este continuta in U(H) atunci F╞═ X V.

Demonstratie. Ca sa constuim H se foloseste V W. H trebuie sa contina atributele din V. De unde rezulta ca H este un graf pe F pentru X V.

Lema 1 nu este aplicabila pentru a deduce secvente derivate, deoarece V W poate sa nu se afle in multimea utila si nu este folosita in deducerea lui X V.

Exercitii.

1.Se considera relatia:

r( A B C D E )

a₁ b₁ c₂ d₁ e₁

a₁ b₂ c₁ d₂ d₁

a₂ b₁ c₃ d₃ e₁

a₂ b₁ c₄ d₃ e₁

a₃ b₂ c₅ d₁ e₁

Care sunt dependentele functionale pe care aceasta relatie le satisface?

2. Sa se demonstreze ca r satiface X Y daca si numai daca X este cheie a relatiei p_XY(r).

Sa se demonstreze ca r satiface X Y pentru orice Y daca si numai daca p_X(r) are acelasi numar de tupluri ca si r.

Sa se demonstreze ca pentru o multime de dependente functionale F data nu exista nici o relatie care sa satisfaca toate dependentele functionale din F^-.

5. Fie F=. Determinati o secventa de inferente a lui AB A si o RAP-secventa de inferente.