Teme programare: Clase de matematica-informatica , intensiv informatica

Teme atestat programare

Clase de matematica-informatica , intensiv informatica

In fisierul IN1.TXT se afla numere naturale situate pe o linie, cu spatiu intre ele. Sa se determine si sa se afiseze, cate dintre aceste numere sunt prime si numerele bine ordonate. (Un numar este bine ordonat daca are cifrele fie in ordine crescatoare, fie in ordine descrescatoare; exemplu:12234 e bine ordonat dar 122324 nu e bine ordonat).

Se citeste un sir de caractere, sa se precizeze daca este palindrom (citit de la dreapta la stanga este la fel ca citit de la stanga la dreapta). Se citeste un caracter , sa se precizeze daca exista in sir si daca da, toate pozitile pe care apare. Daca caracterul citit este litera mica atunci sa se inlocuiasca in sir, aparitia caracterului pe pozitii pare cu acelasi caracter, dar litera mare.

Sa se scrie un program care verifica conjunctura lui Goldbach (aceasta conjunctura consta in posibilitatea scrierii oricarui numar par mai mare decat 2 ca suma a doua numere prime). Se citesc de la tastatura doua numere n si m (m<n<1000), sa se afiseze cato o conjunctura pentru fiecare numar par cuprins intre m si n.

Exemplu: m=700 si n=801; avem: 700=683+17; 702=691+11; 704=701+3; . ; 800=793+7.

"Cifra de control" a unui numar intreg se obtine efectuand suma cifrelor sale, apoi suma cifrelor acestei sume etc. pana se obtine o suma formata dintr-o singura cifra. In fisierul text IN4.TXT se gasesc mai multe numere de cel mult 9 cifre, cate o valoare pe fiecare linie. Se cere sa se scrie in fisierul text OUT4.TXT, pe fiecare rand, cate un numar din fisierul IN.TXT impreuna cu cifra sa de control.

Exemplu: IN4.TXT OUT4.TXT

1938 1938 3

98 98 8

123 123 6

111 111 3

5851 5851 1

Se citesc de la tastatura doua valori a si b, 0<a<b<10000. Dintre toate numerele naturale situate in intervalul [a,b], sa se scrie in fisierul OUT5.TXT, pe prima linie, separate prin spatiu, acele numere cu proprietatea ca suma cifrelor lor este un numar prim, iar pe a doua linie, separate prin spatiu, acele numere care au suma divizorilor para.

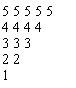Se citeste o valoare s. Sa se scrie un program care tipareste urmatorul triunghi, folosind un subprogram recursiv. Exemplu: pentru s=5 se tipareste:

Se citeste o valoare n. Sa se scrie un program care determina cel mai mic numar natural care are exact n divizori. Programul va repeta citirea lui n si afisarea numarului cu proprietatea ceruta si se va opri atunci cand utilizatorul nu mai doreste repetarea.

Exemplu: pentru n=4 se afiseaza 6; pentru n=5 se afiseaza 16.

Sa se determine c.m.m.d.c. dintre n numere intregi date de la tastatura, fara a folosi nici o structura repetitiva. (indicatie: se folosesc functii recursive).

Se citeste un numar natural nenul n. Sa se genereze si sa se afiseze sirul: , folosind un subprogram recursiv.

In fisierul IN10.TXT pe prima linie se afla o valoare n, iar pe urmatoarele n linii se afla datele despre n elevi; pe fiecare linie este: numele, prenumele, varsta, clasa( in forma 12A, 9C, etc.) unui elev separate intre ele prin cate un spatiu. Sa se citeasca aceste informatii si sa se memoreze. Sa se afiseze (numele prenumele si clasa)elevilor ordonati alfabetic dupa nume, iar daca exista mai multi elevi cu acelasi nume sa se ordoneze crescator dupa clasa. Sa se stearga din vector elevii a caror prenume incepe cu litera A si sa se afiseze elevii ramasi. Sa se calculeze apoi cati elevi (din cei ramasi) au varsta mai mare de 15 ani.

Fiind data o matrice A patratica de ordinul n, sa se calculeze suma elementelor prime de sub diagonala secundara din matrice (inclusiv diagonala) si numarul de elemente divizibile cu 5 din zona de nord a matricii (zona de nord e determinata de intersectia celor doua diagonale).

Exemplu: Fie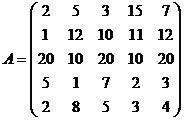

Se citeste de la tastatura un numar n. Sa se determine si sa se afiseze cel mai mare numar obtinut din cifrele lui n, prin rearanjarea lor si sa se precizeze daca numarul obtinut este perfect. (Un numar este perfect daca suma divizorilor sai mai putin el insusi este egala cu numarul; exemplu: numarul 6 este perfect deoarece S=1+2+3=6; numarul 14 nu este perfect S=1+ 2+7=10≠14).

Exemplu. Daca n=2641 se va afisa valoarea 6421 nu este perfect.

Fisierul IN13.TXT contine mai multe siruri de caractere (pe fiecare linie cate un sir). Sa se afiseze pentru fiecare sir, cate o clepsidra din literele sale, in forma urmatoare:

clasa las a las clasa

Exemplu: pentru sirul clasa se va afisa:

Se citesc doua siruri de numere intregi X cu nx elemente si Y cu ny elemente, unde nx>ny. Sa se decida daca Y este subsir al lui X, adica exista un numar k astfel incat:

X_k=Y₁, X_k+1=Y₂ ,., X_k+ny-1=Y_ny.

Daca Y este subsir atunci se va afisa k, altfel se afiseaza un mesaj.

Exemplu: pentru X=(2,7,3,9,10,4,7,8,6,1,9) si Y=(10,4,7) se afiseaza 5; daca Y=(4,7,6,1) se afiseaza 'Nu e subsir'.

In fisierul IN15.TXT se afla mai multe numere naturale din intervalul , scrise pe o singura linie cu spatii intre ele. Sa se creeze fisierul OUT15.TXT care sa contina cate unul pe linie, doar acele numere din fisierul, IN15.TXT, care au suma cifrelor si suma divizorilor un numar par.

Calculati recursiv x^k , valorile x-real si k-intreg se citesc de pe aceeasi linie din fisierul IN16.TXT.

Din fisierul IN17.TXT se citesc mai multe valori separate prin cate un spatiu, care se memoreaza intr-un vector V. Sa se afiseze vectorul V si apoi sa se sorteze crescator elementele pare din vector fara a afecta pozitia elementelor impare, sa se afiseze vectorul sortat.

Se citeste de la tastatura, caracter cu caracter, un sir, citirea se incheie la intalnirea caracterului '$'. Folosind un algoritm recursiv, sa se afiseze in ordine inversa citirii, cifrele care apar in sir.

Exemplu: daca se citeste sirul AB09&2$, se va afisa sirul 290.

Se da o matrice T patratica de ordin n cu elemente numere naturale. Sa se determine vectorul V cu n componente, in care V(i) este egal cu raportul dintre suma elementelor divizibile cu 3 din linia i si suma elementelor prime din coloana i (numarul 1 se va considera prim). Daca suma elementelor din coloana i este 0 atunci V(i) va fi 0.

Exemplu. Daca matricea este 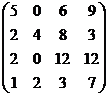atunci V 1.5, 0, 8,0.3).

Din fisierul IN20.TXT se citesc doua siruri de caractere de lungimi egale (cate unul pe linie). Al doilea sir contine numai cifre, in caz contrar programul terminandu-se fara nici o prelucrare si cu un mesaj de eroare. Sa se construiasca si sa se afiseze un al treilea sir, prin repetarea pe rand a fiecarui caracter din primul sir, de un numar de ori egal cu cifra corespunzatoare din al doilea sir.

Exemplu: daca se citesc sirurile 'abcd' si '2403' se va afisa: 'aabbbbddd'