1. m_R(r) m_S(r) oricare ar fi r(R),

2. T_R T_S,

3. FIX(R) FIX(S),

4. R S.

Demonstratie. Din propozitia 1 rezulta ca (1) este echivalenta cu (2). Vom arata ca (1) si (3) sunt echivalente. Din urmatoarea secventa rezulta ca (1)

d1) s FIX( R)

d2) s m_R (s) ( din d1 ),

d3) m_R(s) m_S(s) ( din ipoteza ),

d4) s m_S(s) ( din d2 si d3 ),

d5) s m_S(s ( din lema 1 ),

d6) s m_S(s) ( din d4 si d5 ),

d7) s FIX( S)

Aratam ca (3) (1). Adica din FIX( R) FIX( S) m_R(r) m_S (r).

Fie r(R), r' m_R(r), din idempotenta rezulta m_R(r') r', deci r' FIX( R) din ipoteza rezulta ca r' FIX( S) adica (a) m_S(m_R(r)) m_R(r). Dar m_R(r) r, din monotonia lui m_S rezulta (b) m_S(m_R(r)) m_S(r) ; din (a) si (b) rezulta ca m_S(r) m_R(r).

Vom arata ca conditiile (1) si (4) sunt echivalente. Presupunem ca, dom(A) contine cel putin doua valori pentru orice atribut A din R. Notam aceste valori cu 0 si 1. Construim relatia s(R) cu q tupluri t₁,t₂,.,t_q definite in urmatorul mod :

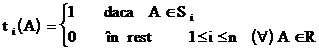
Notam cu t₀ tuplul format numai din valori nule. Nu este greu de verificat ca t₀ apartine lui m_S(s). Prin urmare t₀ m_R(s). Conform definitiei lui m_R, pentru fiecare schema R_i din R exista un tuplu t_j s astfel ca t_j(R_i ) t₀(R_i). Astfel R_i S_j deci S R.

Presupunem ca R S. Fie r(R) o relatie arbitrara si t un tuplu arbitrar din m_S(r). In r exista tuplurile t₁,t₂,.,t_q astfel ca t_i(S_i) t(S_i), 1 i q. Deoarece R S atunci pentru orice R_j din R exista S_i, S_i R_j, prin urmare t_i(R_j) t(Rj). Fie tuplurile t_j' r, t_j'(R_j) t(R_j ) din care rezulta ca t este din m_R(r) si prin urmare m_R(r) m_S(r).

Exercitiu. Fie R si S Daca R S se observa ca T_R(r) T_S(r). Fie relatia r(R) din figura 1 si tablourile T_R(r) si T_S(r).

r(_{A1 A2 A3 A4} ) _TR(_{A1 A2 A3 A4} ) _TS (_{A1 A2 A3 A4} )

3 5 7 9 4 6 8 10

3 5 8 10 4 7 8 11

3 5 8 11

4 6 8 10

4 6 8 11

Figura 1 Figura 2 Figura 3

Corolar 1. Fie multimile de scheme de relatie R si S unde R R₁,R₂,.,R_p S₁,S₂,.,S_q. Urmatoarele afirmatii sunt echivalente :

1. m_R m_S

2. T_R T_S,

3. FIX(R)=FIX(S),

4. R~ S.

Prin conditia (1) intelegem m_R(r) m_S(r) pentru orice r(R).

Fie R si S Multimile de scheme de relatie R si S sunt echivalente. Din corolarul 1 rezulta ca T_R T_S, dar evident ca T_R T_S. Cum se observa din exemplul urmator chiar daca se vor redefini variabilele secundare.

_TR(_{A1 A2 A3 A4} )    _TS (_{A1 A2 A3 A4} )

_{a1 a2 a3 b1 a1 a2 a3 b1}

_{a1 b2 b3 a4 b2 b3 a3 a4}

_{a1 b4 a3 a4 a1 b4 a3 a4}

Figura 1 Figura 2

Definitia 7. Fie w₁ si w doua linii ale tabloului T de schema R. Daca pentru orice atribut A din R cu w₂(A) principala rezulta ca w₁(A) este variabila principala si se spune ca w₁ absoarbe ( subsume ) w₂.

Definitia Fie T un tablou. in care liniile nu mai pot fi ( reduse ) absorbite de nici o alta linie se numeste redus prin absortie si se noteaza cu SUB(T).

Exemplul 6. In tabloul T_R w₁ absoarbe w₂ deoarece w₁(A₁) a₁ w₂(A₁) a₁ w₁(A₄) a₄ w₂(A₄) a₄ atunci :

SUB(T_R)(A₁ A₂ A₃ A₄) SUB(T_S)( A₁ A₂ A₃ A₄)

_{a1 a2 a3 b1 a1 a2 a3 b1}

_{a1 b4 a3 a4 a1 b4 a3 a4}

Teorema 3. Fie multimile de scheme de relatie R si S unde R R₁,R₂,.,R_p S₁,S₂,.,S_q. Atunci:

1) T_R T_S SUB(T_R) SUB(T_S) exceptand variabilele secundare.

2) SUB(T_R) T_R.

Pentru demonstratie vezi Maier/ /.

5. C-Transformari

Teorema 3 arata ca exista un procedeu simplu pentru verificarea echivalentei a doua tablouri obtinute din multimi de scheme si anume verificarea identitatii reduse prin absortie. Orice tablou in care nici o variabila secundara nu se intalneste mai mult decat o data se obtine dintr-o multime oarecare de scheme. Teorema 3 nu este adevarata pentru tablourile unde variabilele secundare sunt duplicate.

Dorim sa formulam conditii de echivalenta pentru tablouri arbitrare introducand c-transformarea pentru tablouri. C-transformarea este asemanatoare evaluarii (estimarii), care in locul transformarii variabilelor tabloului in elemente ale domeniului ele se transforma in variabile ale altui tablou. Prin urmare liniile se transforma in linii.

Definitia 9. Fie T si T' doua tablouri de schema R si multimile de variabile V si V'. Transformarea y :V→V' se numeste c-transformare din T in T' daca ea satisface urmatoarele conditii :

1) daca variabila v se afla in linia A a tabloului T atunci y(v) se afla in linia A a tabloului T' ;

2) daca v este o variabila principala atunci y(v) este variabila principala ;

y(v) T'. Adica, daca y este extinsa la liniile lui T si deci la intregul tablou T atunci prin aceasta transformare o linie din T se transforma intr-o linie din T'.

Exemplul 7 Fie tablourile T si T' din figura 1 si 2 si c-transformarea din figura 3

T(A₁ A₂ A₃ A₄) T'(A₁ A₂ A₃ A₄)

y i

y y

y y y

Figura 1 Figura 2 Figura 3

Primele doua linii din T sunt aplicate in primele doua linii din T' de y, c-transformarea y aplica a treia linie dinT in a doua linie din T'.

Teorema 4. Fie tablourile T si T' de schema R. T T' daca si numai daca exista o c-aplicatie de la T la T'.

Demonstratie. Suficienta. Fie y o aplicatie de la T la T'. Fie r(R) o relatie oarecare, T(r) si T'(r). Daca r este o evaluare a lui T' astfel ca r (T') r, atunci r y este o evaluare pentru T, r y(T) r. Incluziunea rezulta din y(T) T' prin aplicarea lui r. Daca w_d este o linie formata din variabile principale si y( w_d) w_d r y(w_d)) r (w_d) deci T'(r) T(r).

Necesitatea. Presupunem ca T T'. Considerand tabloul T' ca relatie obtinem T(T') T'(T') Luand evaluarea r' care este transformarea identica a variabilelor V' din T'. Evident r'(T') T' T' si r'(w_d) w_d T'(T'). Exista o evaluare r pentru T astfel ca r (T) T', r (w_d) w_d. Atunci definim c-aplicatia din T la T' prin r

Corolar 2. Fie T si T' doua tablouri de schema R. T T' exista o c-transformare de la T la T' si o c-transformare de la T' la T.

Exemplul Fie T tabloul care este compus numai dintr-o linie formata numai din variabile principale w_d si T' un tablou care contine w_d, atunci T T'. C-transformarea din T la T' aplica w_d in w_d. C-transformarea din T' in T aplica toate liniile in w_d.

6. Echivalenta schemelor determinata de restrictii

In acest paragraf se determina care sunt proprietatile unei relatii care sa fie corect reprezentata prin proiectiile sale. Din corolarul 1 rezulta ca, daca R este o schema a bazei de date atunci FIX(R) este multimea tuturor relatiilor pe R R₁,R₂,.R_p numai daca R_i R pentru un i anumit. In multe cazuri dorim sa reprezentam o multime de relatii pentru schema R asupra careia se aplica o multime impusa de restrictii. Vom utiliza restrictiile ca sa reprezentam relatiile.

Definitia 10. Fie P o multime de relatii de schema R. Daca T₁ si T₂ sunt tablouri de schema R atunci T₁ cuprinde peT₂ in raport cu P ( notat T₁⊒_P T₂ ) daca

T₁(r) T₂ (r), r P.

T₁ s_PT₂ ( sunt echivalente pe P ) daca T_{1 P}T₂ si T_{2 P}T₁.

In majoritatea cazurilor se considera P SAT(C) pentru o multime de restrictii C data. Notam pe scurt pe prin . Ne intereseaza cand SAT(C) FIX(R) pentru o schema a bazei de date R. Adica pentru o schema a bazei de date R putem sa descompunem fara pierdere pe R orice relatie din SAT (C). In termenii restrictiilor aceasta se poate reduce la verificarea corectitudinii relatiei C *[R]. Daca T_I este un tablou pentru transformarea identica (T_I contine linia formata din variabile principale), atunci dorim sa stim daca T_R se comporta ca T_I pe SAT(C) adica T_R T_I ? Teorema 3 da un test pentru dar ne trebuie un test pentru . Pentru lema urmatoare va trebui sa privim un tablou ca o relatie care este din multimea P. Prin aceasta se intelege ca pentru orice evaluare r r(T) P Pentru o multime arbitrara de relatii aceste conditii sunt mai greu de verificat. Totusi caand P=SAT(C) unde C consta intr-o multime de F- sau J-dependente daca pentru o evaluare bijectiva r r (T) P, atunci pentru orice alta evaluare r r'(T) P.

Lema 1. Fie T₁ si T₂ doua tablouri de schema R si P o multime de relatii pe R. Fie T₁' si T₂' astfel ca :

1) T₁s_P T₁' si T₂s_P T₂' si

2) T₁' si T₂' considerate ca relatii sunt ambele din P.

Atunci T₁ T₂ daca si numai daca T₁' T₂'.

Demonstratie Suficienta este directa. Daca T₁' T₂' atunci rezulta ca T₁'⊑_P T₂', dar T₁s_PT₁'si T₂s_P T₂' deci T₁⊑_PT₂. Vom arata ca, daca T₁⊑_P T₂ atunci T₁' T₂'. Considerand T₁' simultan ca relatie si tablou atunci T₁'(T₁') este din P si T₁'(T₁') T₂'(T₂'). Fie w_d o linie a tuturor variabilelor principale si r o evaluare identica a lui T₁'. Evident r (T₁') T₁' astfel r (w_d) w_d este in T₁'(T₁') prin urmare si in T₂(T₁'). Exista o evaluare h pentru T₂' astfel ca h( T₂') T₂' si h(w_d) w_d. Evaluarea h poate fi considerata ca o c-transformare din T₂' in T₁' si prin urmare rezulta T₁ * T₂'.

Corolar 3. In ipotezele lemei 1. rezulta ca T₁s_P T₂ daca si numai daca

T₁'s T₂'.

Acest corolar poate fi interpretat ca un test de verificare a relatiei T₁ T₂, daca printr-un procedeu am afla tabloul T', astfel ca T's_CT si T' ca relatie este in SAT(C). Vom introduce reguli de transformare pentru tablouri. O regula de transformare determinata de o multime de restrictii C este un procedeu de modificare a tabloului T in tabloul T' astfel ca Ts_CT'. Prima transformare particulara a fost c-transformarea prin absortie. Pentru un tablou T cu variabile secundare ne duplicate eliminarea liniilor absorbite conserva echivalenta. Va trebui sa gasim multimea regulilor de transformare ( F-reguli si J-reguli) pentru o multime data C de F-dependente si J-dependente. Aplicarea repetata a acestor reguli de transformare are ca rezultat obtinerea unui tablou care satisface toate dependentele din C. In continuare vom considera o multime C de F- si J-dependente pentru o multime U de atribute care constituie schema pentru toate restrictiile si tablourile considerate. Oricarei F-dependente X A din C ii este asociata o F-regula. F-regula determinata de X A reprezinta o clasa de transformari care poate fi aplicata unui tablou care nu depinde de liniile alese.

F-regula

Fie un tablou T care contine liniile w₁ si w₂ unde w₁(X) w₂(X) si v₁ w₁(A) si v₂ w₂ (A), v₁ v₂. A aplica o F-regula determinata de F-dependenta X A la tabloul T, inseamna a identifica variabilele v₁ si v₂ si a inlocui una din ele prin alta in urmatorul mod :

- daca una din v₁ si v₂ este principala, sa zicem v₁ instanta lui v₂ este inlocuita cu v₁.

- daca v₁ si v₂ nu sunt principale atunci orice instanta cu indice mai mare este inlocuita cu instanta variabilei cu indice mai mic.

Deoarece tabloul este o multime de linii, cateva din ele prin redefinire vor fi identice si vor fi eliminate.

Exemplul 9 Fie tabloul T din figura 1 si C . Aplicand F-regula determinata de A₂A₄ A₃ la liniile 1 si 2 permitem inlocuirea variabilei b₃ cu a₃ deoarece a₃ este principala si obtinem tabloul T'.

T(A₁ A₂ A₃ A₄ T'(A₁ A₂ A₃ A₄) T"( A₁ A₂ A₃ A₄

Figura 1 Figura 2 Figura 3

Aplicand F-regula determinata de A₁A₂ A₄ se obtine tabloul T" deoarece variabile b₁ si b₄ trebuie identificate prin cea cu indice mai mic. Astfel prima si ultima linie sunt identice deci se elimina una din ele.

Teorema F. Fie T' tabloul rezultat prin aplicarea unei F-reguli date de X A din tabloul T. Atunci T si T' sunt echivalente pe SAT(X A).

J-regula

Fie S o multime de scheme de relatii si *[S] o J-dependenta pe U. Fie T un tablou si w₁,w₂,.,w_q liniile lui T care sunt unibile pe S cu rezultatul w. Aplicarea J-regulii *[S] la T inseamna formarea tabloului T' T

Exemplul 10. Fie T tabloul reprezentat in figura 4 si C . Aplicand J-regula determinata de *[ A₁A₂, A₂A₃, A₃A₄] la a doua si a treia linie din T genereaza linia <a₁ b₁ b₃ a₄>. Rezultatul este tabloul T' dat in figura 5.

T(A₁ A₂ A₃ A₄ T'(A₁ A₂ A₃ A₄ ) T"( A₁ A₂ A₃ A₄

Figura 4    Figura 5 Figura 6

J-regula data de *[A₁A₂A₄, A₁A₃A₄] poate fi aplicata la prima si a patra linie a lui T'; se genereaza linia <a₁ b₁ b₃ a₄> iar tabloul T' este rezultatul acestei aplicatii.

Teorema J. Fie S Fie T' tabloul rezultat prin aplicarea J-regulii determinata de *[S] din tabloul T. Atunci tablourile T si T' sunt echivalente pe SAT(*[S]).

Demonstratie. Va trebui sa aratam ca T(r) T'(r) pentru orice r SAT(*[S]). Fie t' T'(r) si r o evaluare cu r (w_d) t' si r(T') r. Deoarece T T' avem r(T) r(T') de asemenea r(T') r si r(w_d) t' T(r). Prin urmare T'(r) T(r). Acum fie t un tuplu oarecare din T(r) si r o evaluare cu r(w_d) t si r(T) r. Tuplul unic care ar putea apartine lui r(T') dar nu lui r(T) este r(w) unde w este generata de J-regula determinata de *[S] din liniile w₁,w₂,.,w_q care apartin lui T. Daca w₁,w₂, .,w_q sunt unibile pe S atunci r(w₁), r(w₂),.,r(w_q) unite pe *[S] dau rezultatul w. Intrucat r intra in SAT(*[S]) si r(w₁), r(w₂),., r(w_q) r(T) r atunci r(w) r. Prin urmare r(T') r si r(w_d) t T(r), deci T(r) T'(r) si deci T(r) T'(r).

7. Algoritmul chase

In acest paragraf se da un algoritm de calcul care se bazeaza pe metoda chase, cu ajutorul careia pentru un tablou dat si o multime de dependente C se construieste un nou tablou T* astfel ca T T* si T* ca relatie sa apartina lui SAT(C). Pentru un tablou T si o multime de dependente C se aplica regulile determinate de F- si J-dependentele din C atata timp cat se realizeaza schimbari. Ordinea de aplicare este neesentiala. Conform teoremelor F si J la terminarea algoritmului se genereaza un tablou T* T si T* SAT(C).

Fie tabloul T din figura 1 si C . Aplicand F-regula determinata de BC se obtine T₁ din figura 2. Aplicand J-regula *[ABC, BCD] se obtine T₂ din figura 3. Aplicand F-regula determinata de ADC se obtine T₃ din figura 4.

T ( A B C D) ( A B C D ) ( A B C D ) (A B C D ) T*( A B C D )

b₄

Figura 1 Figura 2 Figura 3 Figura 4 Figura 5

Aplicarea J-regulii determinata de *[ABC, BCD] lui T₃ permite obtinerea lui T* si orice alta regula il lasa invariant. Astfel T* este ca relatie in SAT(C).

Definitia 11. Se numeste secventa generata din T prin aplicarea regulilor ( F- sau J) determinate de dependentele din C, secventa T₀ T,T₁,. .T_i. unde T_i se obtine din T_i-1 prin aplicarea unei F- sau J-reguli determinata de o dependenta din C, se presupune T_i-1 T_i. Ultimul element T_n din secventa generata, care prin aplicarea oricarei F- sau J- reguli determinata de C nu-l mai schimba se numeste chase-ul lui T in raport cu C. Operatorul corespunzator il notam cu (T).

Algoritmul realizat mai jos doua proceduri TR si DIF. Procedura TR transforma tabloul T_j+i in T_j+i+1 pe baza regulei determinata de dependenta C_i. Functia DIF determina daca exista o diferenta intre doua transformari succesive.

0 START [Chase ]

1 INPUT [ T, k, C₁,C₂,.,C_k]

2 n

3 T_n T

4 d

5 WHILE d

5.1 d

5.2 FOR i 1, 2. .., k

5.1.1 CALL TR(T_n,C_i;T*)

5.1.2 IF DIF(T_n,T')

THEN

.1 n n+1

.2 T_n T*

.3 d =0

5.1.3 CONTINUE

5.3 CONTINUE

6 OUPUT

7 STOP

Exemplul 11. Fie T si C din exemplul 1. T, T₁, T₂, T₃ si T* este o secventa generata din T de C si T*IChase_C(T). Va trebui sa observam cum se transforma liniile pe parcursul aplicarii algoritmului Chase. Fie T' obtinut din T prin aplicarea unei J-reguli. Atunci daca w este o linie a lui T ei ii corespunde in T' aceeasi linie sau are in plus o linie obtinuta prin unirea unui numar de linii. Fie T' derivat din T prin aplicarea unei F-reguli care schimba variabila v cu variabila v'. Daca w este o linie in T ii corespunde in T' o linie w' care este de fapt w in care s-a inlocuit v cu v'. ( Daca w nu contine v atunci w w' ).

Daca T₀,T₁,.,T_i,.,T_j este o secventa generata din T determinata de C si este o linie din relatia " corespunde " poate fi prelungita tranzitiv.

Spunem ca linia din corespunde liniei daca exista unde si corespunde lui corespunde , si corespunde lui . Pentru orice linie w dintr-un tablou al secventei generate din T in orice tablou care ii urmeaza exista o linie care ii corespunde.

Teorema 5. Fie tabloul T si retrictiile C. Orice secventa generata din T determinata de C este finita, adica (T)

Demonstratie. Deoarece tablourile sunt multimi finite de linii si orice regula nu introduce noi variabile, exista numai un numar finit de tablouri care pot sa apara in secventa generata din T determinata de C. Este suficient sa aratam ca nici un tablou nu apare de doua ori. Fie si doua tablouri dintr-o secventa generata de din T deterninata de C, i<j. Daca la fiecare pas o F-regula a fost utilizata atunci contine cateva variabile care in lipsesc, deci . Daca in secventa se aplica numai J-reguli atunci contine cel putin o linie in plus fata de , deci

Teorema 6. Orice tablou T* din (T), considerat ca relatie este in SAT(C).

Demonstratie. Daca T* nu ar satisface F-dependenta X A din C atunci ar exista doua linii si in T* astfel ca (X) (X) si (A) (A). Atunci putem aplica F-regula determinata de X A liniilor si care se schimba in T* ceea ce arata ca T* nu este ultimul tablou in secventa generata din T determinata de C. Similar daca T' violeaza o J-dependenta din C atunci aplicand J-regula determinata de F-dependenta respectiva se obtine un nou tablou cu o linie in plus.

Corolar 4. (T) T considerat ca relatie apartine lui SAT(C).

Proprietatea Church-Rosser

Calculul chase-ului este un exemplu de sistem de implicatii. Un sistem de implicatii este o pereche ( Q, ), unde Q este o multime de obiecte si este o relatie binara antireflexiva pe Q, numita relatie de transformare. In cazul nostru calculul chase-ului este un nou sistem de implicatii in raport cu orice multime de restrictii. Multimea Q este formata din tablouri pe U si T T' daca T' se obtine din T prin aplicarea unei F- sau J-reguli determinata de o dependenta din C.

Definitia 12. Inchiderea tranzitiva si reflexiva a relatiei se noteaza . Vom citi T T' prin " T trece in T' " sau " T' este obtinut din T ".

Definitia 13. Fie sistemul de implicatii ( Q, ), obiectul p Q se numeste ireductibil ( terminal ) daca p q implica p q, adica nu exista p q pentru ca sa avem p q.

Definitia 14. Sistemul de implicatii ( Q, ) este finit daca pentru orice p Q exista o constanta c, care depinde de p astfel daca p q in i pasi atunci i c. Adica pentru orice obiect p Q exista numai un numar finit de transformari ale lui intr-un obiect ireductibil (terminal ).

Utilizand teorema 5 din paragraful precedent rezulta ca sistemul de implicatii pentru calculul chase-ului este finit. Prin (T) am notat toate tablourile terminale obtinute din T prin utilizarea F- sau J-regulilor determinate de dependentele din C.

Definitia 15. Un sistem de implicatii ( Q, ) este FCR ( Finit Church-Rosser ) daca pentru orice p Q si daca p si p si si sunt ireductibile atunci Adica incepand cu orice p ajung la unul si acelasi obiect ireductibil independent de procedeul de aplicare a transformarii.

Teorema 7. ( Sethi ) : Sistemul de implicatii ( Q, ) este FCR daca si numai daca pentru orice p Q, p si p exista q Q astfel ca q si q₂ q.

Pentru demonstratie vezi Sethy / /.

Daca T₀,T₁,.,T_i,.,T_j este o secventa generata din T determinata de C si este o linie din , relatia " corespunde " poate fi prelungita tranzitiv.

Spunem ca linia din corespunde liniei daca exista unde si corespunde lui corespunde , si corespunde lui . Pentru orice linie w dintr-un tablou al secventei generate din T in orice tablou care ii urmeaza exista o linie care ii corespunde.

Teorema Calculul chase-ului determinat de o multime de restrictii C este un sistem de implicatii FCR. Prin urmare este un singleton.

Demonstratie. Trebuie sa aratam ca calculul chase-ului este un sistem de implicatii finit. Adica va trebui sa aratam ca, daca din tabloul T se obtin tablourile si prin aplicarea unor reguli de transformare determinate de dependentele din C atunci exista un tablou T* care poate fi obtinut din T₁ sau T₂ prin aplicarea a uneia sau mai multor reguli de transformare determinate de C.

Pentru aceasta vom examina trei cazuri.

T T T

F-regula F-regula F-regula J-regula J-regula J-regula

T₁ T₂ T₁ T₂ T₁ T₂

Cazul 1 Cazul 2 Cazul 3

Se observa ca J-regulile lasa neschimbate liniile si ca o F-regula nu poate schimba ocurenta unei unei variabile fara a o schimba pe cealalta. Fie w₁ si w₂ doua linii in T si u₁ si u₂ linii in T' corespunzatoare lui w₁ si w₂ unde T' este obtinut din T prin aplicarea unei F- sau J-reguli. Deoarece daca w₁(X) w₂(X) atunci u₁(X) u₂(X) rezulta ca daca o F- sau J-regula este aplicata la o multime de linii in T atunci aceeasi regula este aplicabila la multimea de linii corespunzatoare lui T'.

Cazul 1: Fie T₁ dedus din T prin aplicarea regulii X A cu variabilele v₁ si v₂, si T₂ dedus din T prin aplicarea regulii Y B cu variabilele v₃ si v₄. Daca A B se utilizeaza regula dedusa din X A pentru a identifica variabilele v₁ si v₂. Rezultatul este T*. Analog plecand

de la T₁ prin aplicarea lui Y B se identifica v₃ si v₄. Daca A B se aplica succesiv regulile X A si Y B cel mult de doua ori si se obtine T*.

Celelalte cazuri sunt simple exercitii.

Corolar 5. Daca SAT(C) SAT(C') atunci (T) (T) pentru orice tablou T.

Demonstratie: Vom da demonstratia in cazul cand C' C pentru orice c cu proprietatea C c. Fie T* (T). Aplicarea acelorasi reguli determinate de C la tabloul T conduce la obtinerea lui T*, deoarece C' C. Din teorema 6 rezulta ca nu putem aplica o regula din C' la T*, deoarece T* ca relatie este in SAT(C) si prin urmare in SAT(C'). Deci (T) T*.

9. Echivalenta tablourilor determinata de restrictii

Vom testa echivalenta tablourilor determinata de o multime de restrictii, care constituie un test pentru cazul cand transformarea m_R este fara pierderi de informatii pe SAT(C). Din observatiile de la inceputul acestui paragraf se stie ca T (T). Din lema 1 rezulta urmatoarea teorema :

Teorema 9. Fie tablourile T₁ si T₂ si C o multime de restrictii.

T₂⊑_CT_{1 dac}a s_{i numai dac}a Chase_C(T₂) Chase_C(T₁).

Corolar 6. T₁ T₂ Chase_C(T₁) Chase_C(T₂)

Vom da un procedeu de a verifica cand toate relatiile din SAT(C) pot fi corect reprezentate prin proiectiile lor dupa schemele de relatie ale unei baze de date de schema R. Aceasta conditie este echivalenta cu C *[R] sau ca este aplicatia identica pe SAT(*[C]). In termenii echivalentei tablourilor T_Rs_CT_I unde T_I este tabloul compus din w_d linia variabilelor principale. T_I este aplicatia identica a tuturor relatiilor.

Dintr-o teorema 8 rezulta ca pentru a testa echivalenta este suficient Chase_C(T_I) T_I. Verificarea conditiei Chase_C(T_R) T_I se reduce la a verifica ca Chase_C(T_R) contine w_d.

10. Verificarea implicatiei dependentelor functionale

Fie C o multime de dependente functionale. Vom introduce un test pentru verificarea unei F-dependente din multimea C. Prezentam lema pe baza careia se demonstreaza teorema de caracterizare a implicatiei.

Lema 2. Fie T un tablou si C o multime de restrictii. Fie ρ o evaluare a tabloului T astfel ca ρ(T) r unde rISAT(C). Daca este o secventa generata pentru (T), atunci pentru 0 i n :

ρ (w_i) si w_i absoarbe unde w₀ este o linie oarecare in si w_i este

linia care-i corespunde in

r;

, i n.

Demonstratie. Pentru a demonstra (1) si (2 ) este suficient sa aratam ca, daca este o linie din si este linia care-i corespunde in atunci ρ ( ) si absoarbe . Daca w este o linie in care nu corespunde la nici o linie in , atunci ρ(w) r. Daca este obtinut prin aplicarea unei F-reguli care nu schimba variabilele in , atunci , si deci ρ( absoarbe . In caz contrar, deoarece trece in , pentru un atribut A (A) se schimba din in . Schimbarea se face prin aplicarea F-regulii determinata de F-dependenta X A atunci pentru liniile si in in care (X) (X) si (A) si (A) si ρ( unde si sunt tupluri din r. Va trebui sa avem (X) (X) deoarece r este in SAT(C) si (A) (A). Deci ρ( (A)) (A) (A) (A)) ). Prin urmare ρ( ). Daca w este o linie in care nu corespunde nici unei linii din atunci w este rezultatul unei uniri si deci apartine lui SAT(C).

Fie dependenta netriviala X A si dorim sa testam cand C X A. Construim tabloul care este format din doua linii si . Linia este formata numai din variabile principale si are variabile principale numai in coloanele care apartin lui X. Adica , R

Teorema 10. C X A daca si numai daca (T_X) contine in coloana lui A numai variabile principale.

Demonstratie. Fie T ). Presupunem ca T* are variabile secundare in coloana A. T* este considerat ca relatie este contraexemplu pentru C X A. Din teorema 6 rezulta ca T* satisface C. Prin urmare orice linie a lui T* are toate simbolurile principale in coloanele lui X, deoarece calculul chase-ului nu creaza noi simboluri. Din lema 2 rezulta ca linia ramane neschimbata. Prin urmare T* are doua linii compatibile pe X si necompatibile pe A, deci T* contrazice X A. Presupunem ca T* are numai variabile principale in coloana X si r o relatie arbitrara din SAT(C). Fie si cu (X) (X), r. Consideram ρ o evaluare a lui astfel ca ρ( si ρ( . O astfel de evaluare exista deoarece (X) (X). Iar este linia din T* este linia care corespunde lui din . Fie * linia din * care corespunde lui din . Din lema 2 ρ( ) si T* are aceleasi variabile in coloana A, (A) *(A).

(A) (A)) (A)) (X)) (A)

Astfel doua tupluri din r compatibile pe X sunt comparibile pe A. Prin urmare deoarece r a fost arbitrar aleasa rezulta SAT(C) SAT(X A) sau C X A.

Pe aceasta teorema se bazeaza urmatorul algoritm :

0 PROCEDURE TID ( X, A, C, n ;w) /*-Testarea implicatiei C X A */

1 Call generare(X,n;T_X)

2 CALL Chase( C, ; T, p) /p-reprezinta nr de linii ale chase-ului/

3 d

4 i

5 WHILE d

5.1 IF T( i, A ) a_A

THEN

.1 d

ELSE

.2 IF i p

THEN

.2.1 i i + 1

ELSE

.2.2 d

6 IF d

THEN

6.1 w TRUE

ELSE

6.2 w FALSE

7 RETURN(w)

0 Procedure generare(X,n;T_X)

1 k

2 FOR i 1, 2,, n

( 1, i )

2.2 IF X

THEN

( 2, i )

ELSE

.2 k k + 1

( 2, i )

2 Return

Exemplul 12. Fie C si dorim sa aratam ca C BC D. In acest caz . Exista in coloana D astfel ca BC D nu este implicata de C. Daca C' atunci ) este T*.

T* ( A B C D )

T* are numai in coloana D, deci C BC D.

Pana acum am definit inchiderea lui X numai in raport cu o multime de F-dependente. Vom extinde definitia pentru a cuprinde si J-dependente.

Definitia 16. Fie C o multime de F-dependente si J-dependente si X o multime de atribute. Se numeste inchidere a lui X determinata de C, notata , cea mai mare multime Y cu proprietatea C X Y.

Observatie. Daca C este formata numai din F-dependente, aceasta definitie se reduce la vechea definitie.

Corolarul 7. Pentru o multime data C, este formata din toate atributele A pentru care ) are numai variabile principale.

Corolarul Daca J este o multime de J-dependente, atunci J X Y implica X Y. Adica o multime de J-dependente implica numai F-dependente triviale.

Demonstratie. Deoarece ) are o variabila secundara in orice coloana corespunzatoare lui U, X , deoarece J regula nu identifica simboluri. Deoarece dependentele multivoce sunt cazuri speciale de J-dependente vom putea testa C X Y prin testarea lui C* [ XY, XZ], unde Z U-XY.

Teorema urmatoare arata o cale alternativa care utilizeaza Chase pentru a gasi intreaga multime Y astfel ca C X --Y, pentru un X dat.

Teorema 11. Fie C o multime de restrictii si fie Y o multime disjunctiva de multimea determinata de C. C X Y daca si numai daca contine o linie cu variabile principale numai in coloana Y .

Demonstratie. Necesitatea. Fie ). Fie si liniile corespunzatoare lui si din . Fie schema bazei de date R unde Z U-Y . Vom arata ca ) trebuie sa contina . Prin urmare C [XY,XZ]. Fie si liniile in pentru schemele XY si XZ si fie si liniile in . Se considera aplicatia δ de la variabile din la variabile din data de δ( . Daca este considerat ca relatie atunci δ poate fi privita ca o evaluare si deoarece (X) (X) rezulta (X) (X). Prin urmare T* considerat ca relatie este in SAT(C), din lema 1 δ( (X), δ( ) si δ( ). Deoarece ). Se vede ca aplica variabilele principale din coloanele lui in ale lui * si variabilele principale din coloanele lui in ale lui *. Vom arata ca linia a lui are variabile principale in coloanele Y ) este linia din *. Deoarece contine variabile principale in coloanele ) contine variabile principale in coloanele lui . Deoarece absoarbe contine p-variabile in coloanele din Y. Se stie ca δ( , δ aplica p-variabilele din Y in coloanele Y ale lui *. Linia contine variabile principale in coloanele Y, astfel δ( ) este variabila principala in toate coloanele Y. Deoarece absoarbe este formata din variabile principale in toate coloanele lui Z. Este cunoscut ca δ( , de aceea δ trebuie sa aplice variabile principale din coloana Z a lui in variabile principale ale coloanelor lui Z ale lui *. Linia este neprincipala in coloanele Z. U=Y Z, astfel δ ( ) este d-principala in coloanele Z. Prin urmare contine , astfel C X Y.

Implicatia inversa. Presupunem C X Y. Fie C'= C *[ XY, XZ], unde Z=U- Y. Din corolarul 6 rezulta ca ) deoarece SAT(C) =SAT(C').

0 PROCEDURE INCHIDERE ( X, C,n ; , k )

1 CALL generare(X,n;T_X )

2 CALL ; T*, m )

3 k

5 FOR j = 1, 2,, n

5.1 d

5.2 i

5.3 WHILE d=1 & i m

5.3.1 IF

THEN

5.3.1.1 d

ELSE

5.3.1.2 i i + 1

5.3.2 CONTINUE

5.4 IF d = 1

THEN

5.4.1 k k + 1

5.4.2

5.5 CONTINUE

6 RETURN

Teorema 11 sta la baza urmatorului algoritm de verificare a implicatiei C X--Y.

0 START [ TIDM - Testerea Implicatiei MV-dependentei ]

1 INPUT

2 CALL generare ( X,n ; ) //genereaza

3 CALL Chase(C, ; T*, m )

4 CALL INCHIDERE ( X, C ; , k )

5 i

6 d

7 WHILE i n & d=2

7.1 j 1 w

7.2 WHILE w=0 & j n

7.2.1 IF Y

THEN

.1 IF

THEN

.1.1 w

ELSE

.1.2 j j+1

.2 CONTINUE

7.2.2 CONTINUE

7.3 IF w = 0

THEN

7.3.1 d

ELSE

7.3.2 i i 1

7.4 CONTINUE

8 CASE d OF

1 OUTPUT

2 OUTPUT

9 STOP

11. Tabloul ca patern al unei relatii

In acest paragraf se formalizeaza ideea tabloului ca patern (sablon) al unor relatii.

Definitia 17. Fie P o multime de relatii si r o relatie oarecare. Relatia s din P se numeste completare a lui r in P daca r s si nu exista nici o relatie s'IP astfel ca r s' s. Multimea tuturor completarilor se noteaza cu (r). Scrierea prescurtata a lui (r) este COMP(r). Completarea nu exista intotdeauna.

Exemplul 13 Fie relatia r din figura 1). Daca C = atunci (r)= . Daca C = [ AB, BCD ] atunci (r)= s din figura 2.

r ( A B C D ) s ( A B C D ) Q ( A B C D )

4 6 8 2 4 6 8 2 4 6 8

Figura 1 Figura 2 Figura 3

Daca o completare exista ea nu este unica.

Exemplu 14 Fie relatia din figura 1 si P = SAT([AB, BC]). Completarea (r) contine relatia s din figura 2 si relatia q din figura 3.

O multime P de relatii se numeste inchisa in raport cu intersectia daca pentru orice pereche de relatii r si s din P r s este in P.

Lema 3. P este inchisa in raport cu intersectia daca si numai daca completarea in raport cu P este unica.

Demonstratie. Presupunem ca P este inchisa fata de intersectie. Fie s si s' completari ale lui r in raport cu P. Din inchidere rezulta s' s P si s' s r, astfel ca s= s' s = s'. Fie r si s din P si q= r s. Exista o submultime r' a lui r ( care poate fi r insasi) astfel ca r' este o completare a lui q in raport cu P. Analog exista s' in P care este o completare a lui q. Din ipoteza de unicitate rezulta s'= r', de unde s'= q'= r', deci q apartine lui P.