| CATEGORII DOCUMENTE |
| Arhitectura | Auto | Casa gradina | Constructii | Instalatii | Pomicultura | Silvicultura |
| Cadastru |
Curbele de nivel sau izohipsele sunt linii care unesc puncte cu aceeasi altitudine. Ele rezulta din proiectarea pe plan a tuturor punctelor provenite din intersectia suprafetei terestre cu o serie de planuri orizontale, paralele si echidistante (Figura 7). Echidistanta poate fi definita ca distanta care separa planurile imaginare de sectionare a reliefului. Ea este de doua feluri : naturala si grafica.
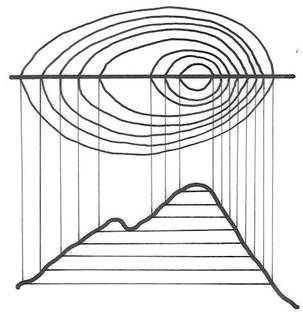
Figura 7 - Principiul metodei curbelor de nivel
Echidistanta naturala este valoarea in metri care desparte planurile de sectionare a formelor de relief, iar cea grafica este valoarea echidistantei naturale redusa la scara hartii. Echidistanta este influentata de scara si de forma de relief reprezentata. Astfel, pe hartile la scara 1 : 10 000 ea este de 2,5 m, pe cele la scara 1 : 25 000 are valoarea de 2,5 sau 10 m, la scara 1 : 50 000, de 10 sau 20 m, iar la scara 1 : 100 000, de 20 sau 40 m. In zonele cu relief muntos echidistanta este mai mare decat in zonele joase si relativ netede. Spre deosebire de hartile topografice, pe cele geografice echidistanta nu se mentine aceeasi, ci devine din ce in ce mai mare pe masura cresterii altitudinii.
Curbele de nivel sunt de mai multe feluri, in functie de importanta lor, si anume: curbe de nivel principale, normale, secundare sau ajutatoare si accidentale (Figura 8).
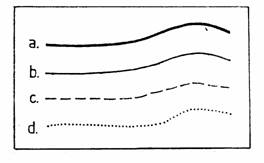
Figura 8 - Tipuri de curbe de nivel
a - principala ; b - normala ; c - ajutatoare ; d - accidentala
Curbele de nivel principale sunt trasate cu o linie continua mai groasa de culoare maro-roscat. Din loc in loc ele sunt intrerupte pentru a se putea inscrie valorile de altitudine respective.
Curbele de nivel normale se deseneaza cu o linie continua de culoare maro-roscat, dar mai subtire decat cea prin care se reprezinta curbele principale. Intre doua curbe de nivel principale se gasesc patru curbe de nivel normale.
Curbele de nivel secundare sau ajutatoare se traseaza prin linii intrerupte. Echidistanta lor este egala cu jumatate din echidistanta curbelor normale.
Curbele de nivel accidentale sunt redate prin linii punctate sau intrerupte. In cazul acestora din urma segmentele sunt mai mici decat cele ale curbelor secundare. Echidistanta curbelor accidentale este egala cu un sfert din cea a curbelor normale. Totusi, curbele accidentale, asa cum indica si numele, sunt utilizate ori de cate ori este nevoie sa se scoata in evidenta anumite "accidente" de relief, adica neregularitati ale scoartei terestre avand echidistante mai mici decat un sfert din echidistanta curbelor normale. In aceste situatii se recomanda ca pe curbele accidentale sa se inscrie valorile de altitudine respective.
In Figura 9 pot fi urmarite formele de relief care rezulta din modul in care se combina curbele de nivel.

Figura 9 - Sector de harta in curbe de nivel
1 - vale cu curs temporar ; 2 - sa ; 3 - cota ; 4 - mamelon ;
5 - vale cu curs permanent ; 6 - bot de deal ; 7 - curba de
nivel principala ; 8 - curba de nivel normala ; 9 - pinten ;
10 - culme ; 11 - bergstrich ( indicator de panta ) ; 12 - confluenta
Cunoasterea proprietatilor curbelor de nivel da posibilitatea descifrarii mai rapide si mai exacte a reliefului de pe planurile si hartile topografice. Dupa A.Nastase (1983), aceste proprietati sunt :
deplasandu-ne pe o curba de nivel, nici nu urcam si nici nu coboram ;
pe orice drum s-ar merge intre doua curbe de nivel se va parcurge aceeasi altitudine egala cu echidistanta ;
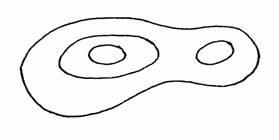
curbele de nivel care se opun fata in fata sunt egale ca valoare (Figura 10);
curbele de nivel se pot atinge, dar nu se pot intretaia ( exceptie facand reprezentarea stancilor aplecate ) ;
![]()
Figura 10 - Curbe de nivel care se opun fata in fata
curbele de nivel inainteaza pe dealuri ( au o forma convexa ) si se retrag pe vai ( au o forma concava ) ;
cu cat curbele de nivel sunt mai dese, cu atat panta este mai mare, si invers, cu cat sunt mai rare, cu atat panta este mai lina (Figura 7) ;
cu cat curbele de nivel sunt mai multe, cu atat altitudinea este mai mare si cu cat sunt mai putine, cu atat altitudinea este mai mica (cu conditia ca echidistanta sa fie aceeasi) ;
cifrele care indica valorile curbelor de nivel sunt astfel dispuse incat baza lor este asezata spre piciorul pantei.
Citirea curbelor de nivel este mult usurata de prezenta indicatoarelor de panta, care mai sunt cunoscute si sub denumirea de bergstrich - uri. Acestea sunt niste liniute dispuse perpendicular pe curbele de nivel, avand rolul de a indica sensul in care coboara panta (Figura 11).
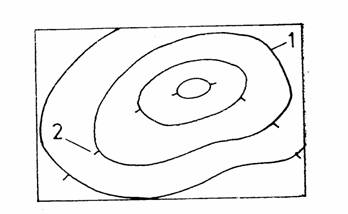
Figura 11 - Indicatoare de panta ( bergstrich - uri )
1 - curbe de nivel ; 2 - bergstrich - uri
Avantajul metodei curbelor de nivel este acela ca da posibilitatea rezolvarii unor probleme de ordin practic, cum ar fi : determinarea diferentelor de nivel dintre puncte, calculul altitudinii punctelor si pantelor dintre acestea, construirea profilelor, etc.
Un mare dezavantaj al acestei metode consta in faptul ca reprezentarea reliefului nu este sugestiva. Cu alte cuvinte, atunci cand privim o harta pe care sunt trasate curbe de nivel nu sesizam la prima vedere aspectul reliefului, fiind nevoie sa procedam la o descifrare a acestuia. De asemenea, metoda curbelor de nivel nu da posibilitatea reprezentarii suprafetelor plane si a celor puternic inclinate. In cazul suprafetelor plane, din cauza denivelarilor extrem de reduse, harta aproape ca va fi lipsita de curbe de nivel, ceea ce ar crea falsa impresie ca in acea zona suprafata terestra este perfect orizontala. Pentru a se inlatura acest neajuns se recurge, de obicei, la indesirea cotelor.
In cazul suprafetelor puternic inclinate, curbele de nivel vor fi extrem de apropiate sau chiar se vor suprapune, astfel incat in acele zone harta isi va pierde expresivitatea. De aceea, reprezentarea pe harta a abrupturilor, viroagelor si a altor accidente de relief se va face prin hasuri sau semne speciale.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 6401
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved