DISTRIBUTIA TEMPERATURII INTR-O PLACA METALICA DREPTUNGHIULARA CU SURSA DE CALDURA

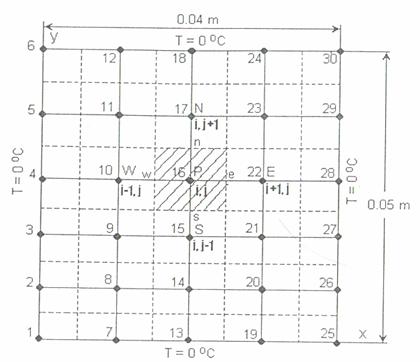
DISTRIBUTIA TEMPERATURII INTR-O PLACA METALICA DREPTUNGHIULARA CU SURSA DE CALDURA

Se considera o placa metalica dreptungiulara de dimensiuni 0,05 x 0,04[m].Conductivitatea termica a placii este = 4[W/m/K]. Toate frontierele placii sunt mentinute la temperatura constanta de 0 C si termenul sursa este S=40∙10⁶[W/m³].

Sa se calculeze distributia stationara de temperatura in placa folosind reteaua de dicretizare

din figura de mai jos(Δx=Δy=0,01 m).

Rezolvare :

Ecuatia conductiei termice stationare 2D pentru conditiile enuntate este :

Ecuatia discretizata pentru un nod interior (de exemplu :nodul 16) este urmatoarea :

a_pT_p= a_wT_w+ a_ET_E+ a_ST_S+ a_NT_N+ b

sau:

; ; ; ; a_p=a_W+a_E+ a_S+ a_N ; b=

Termenul sursa ,S fiind constant,nu este necesar sa fie liniarizat. Valorile coeficientilor sunt:

a_w = a_E = a_S = a_N =4 ; a_p=16 ; b=4000

Rezulta sistemul de ecuatii:

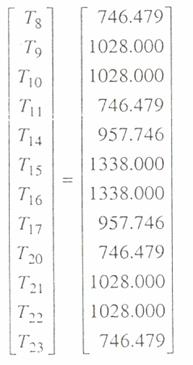
Solutia sistemului este:

PROGRAMUL IN FORTRAN:

parameter (nnx=21,nny=26,nit=1500)

double precision temp(nnx,nny),ax(nnx,nny),ay(nnx,nny)

double precision a(nnx,nny),b(nnx,nny),c(nnx,nny),wk(nnx,nny)

double precision a1(nny),b1(nny),c1(nny),wk1(nny),temp1(nny)

double precision dif(nnx,nny),temp2(nnx,nny)

double precision dx,dy,tb,l,h,la,gz,s,err

data tb/0.0/,l/0.04/,h/0.05/,la/4.0/,gz/1.0/,err/0.001/

data s/40000000.0/

c ----- ----- -------calculul pasului dx si dy-------- ----- ------ ----- ----- -----

dx=l/(nnx-1)

dy=h/(nny-1)

write(*,*)'dx=',dx

write(*,*)'dy=',dy

c----- ----- -------initializarea temperaturii-------- ----- ------ -----------

do i=1,nnx

do j=1,nny

temp(i,j)=0.01

enddo

enddo

c-----------introducerea conditiilor de tip Dirichlet-------- ----- ------ -

c----- ----- -------frontiera NORD-------- ----- ------ ----- ----- ----------

do i=1,nnx

temp(i,nny)=tb

enddo

c-------- frontiera SUD-------- ----- ------ ----- ----- --------- ----- --------

do i=1,nnx

temp(i,1)=tb

enddo

c--------- frontiera WEST-------- ----- ------ -------- ----- ------ -

do j=1,nny

temp(1,j)=tb

enddo

c--------- frontiera EST-------- ----- ------ -------- ----- ------ ---------

do j=1,nny

temp(nnx,j)=tb

enddo

c==================bucla de iteratie==============================

do k=1,nit

c------------formarea diagonalelor vectorilor -------- ----- ------ ----- ----- -------

do i=2,nnx-2

if(i.eq.2)then

c-------------diagonala inferioara ' a'-------- ----- ------ ----- ----- -----------

do j=2,nny-1

if(j.eq.2)then

a(i,j)=0.0

a1(j-1)=a(i,j)

else

a(i,j)=-la*(dx*gz)/dy

a1(j-1)=A(i,j)

endif

enddo

c-----------diagonala superioara 'c' -------- ----- ------ ----- ----- ------------

do j=2,nny-2

if(j.eq.2)then

c(i,j)=-la*(dx*gz)/dy

c1(j-1)=c(i,j)

else

c(i,j)=-la*(dx*gz)/dy

c1(j-1)=c(i,j)

endif

enddo

c(i,nny-1)=0.0

c1(nny-2)=c(i,nny-1)

c------------- diagonala principala 'b'-------- ----- ------ ----- ----- -------------

do j=2,nny-1

if(j.eq.2)then

b(i,j)=2.0*la*(dy*gz)/dx+2.0*la*(dx*gz)/dy

b1(j-1)=b(i,j)

else

b(i,j)=2.0*la*(dy*gz)/dx+2.0*la*(dx*gz)/dy

b1(j-1)=b(i,j)

endif

enddo

c---------formarea initiala a vectorului termenului liber (wk)----

do j=2,nny-2

if (j .eq. 2) then

wk(i,j) = (la*(dx*gz)/dy)*temp(i,j-1) +

* (la*(dy*gz)/dx)*temp(i-1,j) +

* (la*(dy*gz)/dx)*temp(i+1,j) + s*dx*dy*1.0

wk1(j-1) = wk(i,j)

else

wk(i,j) = (la*(dy*gz)/dx)*temp(i-1,j) +

* (la*(dy*gz)/dx)*temp(i+1,j) + s*dx*dy*1.0

wk1(j-1) = wk(i,j)

endif

enddo

wk(i,nny-1) = (la*(dy*gz)/dx)*temp(i-1,nny-1) +

* (la*(dy*gz)/dx)*temp(i+1,nny-1) +s*dx*dy*1.0+

* (la*(dx*gz)/dy)*temp(i,nny)

wk1(nny-2) = wk(i,nny-1)

c------------- solutia sistemului -------- ----- ------ ----- ----- ----- ----- -------

CALL TRIDAG (a1,b1,c1,wk1,temp1,nny-2)

c-------formarea solutiei finale pentru toate liniile verticale ----- ----- ------------

do j = 2,nny-1

temp(i,j)=temp1(j-1)

enddo

else

c---------diagonala inferioara 'a' -------- ----- ------ ----- ----- ---------

do j = 2,nny-1

if (j .eq. 2) then

a(i,j) = 0.0

a1(j-1) = a(i,j)

else

a(i,j) = - la*(dx*gz)/dy

a1(j-1) = a(i,j)

endif

enddo

c---------diagonala superioara 'c'-------- ----- ------ ----- ----- ----- ----- ----

do j = 2,nny-2

if (j .eq. 2) then

c(i,j) = - la*(dx*gz)/dy

c1(j-1) = c(i,j)

else

c(i,j) = - la*(dx*gz)/dy

c1(j-1) = c(i,j)

endif

enddo

c(i,nny-1) = 0.0

C1(nny-2) = C(i,nny-1)

c----------diagonala principala 'b' -------- ----- ------ ---

do j = 2,nny-1

if (j.eq.2)then

b(i,j) = 2.0*la*(dy*gz)/dx+2.0*la*(dx*gz)/dy

b1(j-1) = b(i,j)

else

b(i,j) = 2.0*la*(dy*gz)/dx + 2.0*la*(dx*gz)/dy

b1(j-1) = b(i,j)

endif

enddo

c-----formarea initiala a vectorului termenului liber (wk)----- ----- -------

do j = 2,nny-2

if (j .eq. 2) then

wk(i,j) = (la*(dx*gz)/dy)*temp(i,j-1) + (la*(dy*gz)/dx)*temp(i-1,j) +

* (la*(dy*gz)/dx)*temp(i+1,j) + s*dx*dy*1.0

wk1(j-1) = wk(i,j)

else

wk(i,j) = (la*(dy*gz)/dx)*temp(i-1,j) +

* (la*(dy*gz)/dx)*temp(i+1,j) + s*dx*dy*1.0

wk1(j-1) = wk(i,j)

endif

enddo

wk(i,nny-1) = (la*(dy*gz)/dx)*temp(i-1,nny-1) +

* (la*(dy*gz)/dx)*temp(i+1,nny-1) +s*dx*dy*1.0+

* (la*(dx*gz)/dy)*temp(i,nny)

wk1(nny-2) = wk(i,nny-1)

c------------- solutia sistemului -------- ----- ------ ---

CALL TRIDAG (a1, b1, c1, wk1, temp1, nny-2)

c-------formarea solutiei pe toate liniile verticale----- ----- --------- ----- --------

do j = 2,nny-1

temp(i,j)=temp1(j-1)

enddo

endif

enddo

c==================pentru ' i = nnx-1' =========================

c---------diagonala inferioara'a' -------- ----- ------ ----

do j = 2,nny-1

if (j .eq. 2) then

a(nnx-1,j) = 0.0

a1(j-1) = a(nnx-1,j)

else

a(nnx-1,j) = - la*(dx*gz)/dy

a1(j-1) = a(nnx-1,j)

endif

enddo

c---------diagonala superioara 'c' -------- ----- ------ ----

do j=2,nny-2

if (j .eq. 2) then

c(nnx-1,j) = - la*(dx*gz)/dy

c1(j-1) = c(nnx-1,j)

else

c(nnx-1,j) = - la*(dx*gz)/dy

c1(j-1) = c(nnx-1,j)

endif

enddo

c(nnx-1,nny-1) = 0.0

c1(nny-2) = c(nnx-1,nny-1)

c----------diagonala principala 'b' -------- ----- ------ ----- ----- ----

do j = 2,nny-1

if (j.eq.2)then

b(nnx-1,j) = 2.0*la*(dy*gz)/dx + 2.0*la*(dx*gz)/dy

b1(j-1) = b(nnx-1,j)

else

b(nnx-1,j) = 2.0*la*(dy*gz)/dx + 2.0*la*(dx*gz)/dy

b1(j-1) = b(nnx-1,j)

endif

enddo

c-----formarea initiala a vectorului termenului liber (wk)----- ----- -------

do j = 2,nny-2

if (j .eq. 2) then

wk(nnx-1,j) = (la*(dx*gz)/dy)*temp(nnx-1,j-1) +

* (la*(dy*gz)/dx)*temp(nnx-2,j) +

* (la*(dy*gz)/dx)*temp(nnx,j) + s*dx*dy*1.0

wk1(j-1) = wk(nnx-1,j)

else

wk(nnx-1,j) = (la*(dy*gz)/dx)*temp(nnx-2,j) +

* (la*(dy*gz)/dx)*temp(nnx,j) + s*dx*dy*1.0

wk1(j-1) = wk(nnx-1,j)

endif

enddo

wk(nnx-1,nny-1) = (la*(dy*gz)/dx)*temp(nnx-2,nny-1) +

* (la*(dy*gz)/dx)*temp(nnx,nny-1) + s*dx*dy*1.0+

* (la*(dx*gz)/dy)*temp(nnx-1,nny)

wk1(nny-2) = wk(nnx-1,nny-1)

c------------- solutia sistemului -------- ----- ------ ---

CALL TRIDAG (a1, b1, c1, wk1, temp1, nny-2)

c-------formarea solutiei pe toate liniile verticale--------

do j = 2,nny-1

temp(i,j)=temp1(nnx-1)

enddo

c--------verificarea cu criteriul convergentei ----- ----- --------- ----- ----

do i=2,nnx-1

do j = 2,nny-1

dif(i,j) = abs(100.0*(temp(i,j) - temp2(i,j))/temp(i,j))

enddo

enddo

difmax = dif(2,2)

do i=2,nnx-1

do j=2,nny-1

if(dif(i,j) .gt. difmax) then

difmax = dif(i,j)

else

endif

enddo

enddo

write(*,*)'iter, difmax, err', k, difmax, err

write(*,*)'iter, difmax, err', difmax, err

if (difmax .le. err) then

write(*,*)'sortie par critere de convergeance, k=',k

goto 100

else

endif

c =========actualizarea temperaturii de la pasul precedent==================

do i=2,nnx-1

do j=2,nny-1

temp2(i,j) = temp(i,j)

enddo

enddo

c-------bucla fina de iteratie 'nit' -------- ----- ------ ----- ----- --------- ----- -------

enddo

100 continue

c----- ----- -------- scrierea solutiei -------- ----- ------ ----- ----- ----- ----- -------

OPEN(20,file='2Ds2.prn')

do i=1,nnx

write(20,101)(temp(i,j),j=1,nny,2)

enddo

CLOSE(20)

101 format(26(1x,F7.2))

STOP

END

SUBROUTINE TRIDAG(a,b,c,r,u,n)

parameter (nmax = 200000)

integer j

double precision a(n),b(n),c(n),r(n),u(n)

doubleprecision bet,gam (nmax)

if (b(1).eq.0.)pause 'tridag:rewrite equations!'

bet =b(1)

u(1)=r(1)/bet

do j=2,n

gam (j)=c(j-1)/bet

bet =b(j)-a(j)*gam(j)

if (bet.eq.0.) pause 'tridag failed'

u(j)=(r(j)-a(j)*u(j-1))/bet

enddo

do j=n-1,1,-1

u(j)=u(j)-gam(j+1)*u(j+1)

enddo

return

end

Solutia in Mathcad:

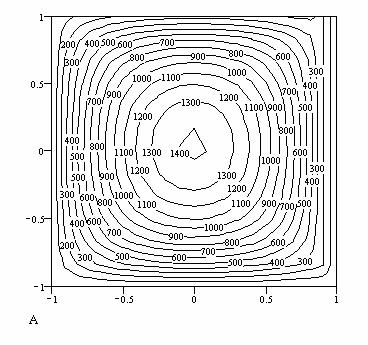
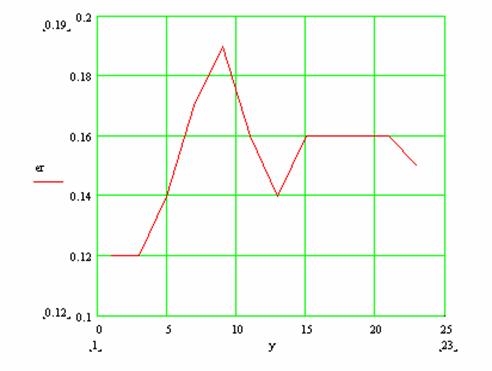
Erorile :

Distributia temperaturii in QuickField