| CATEGORII DOCUMENTE |
| Arhitectura | Auto | Casa gradina | Constructii | Instalatii | Pomicultura | Silvicultura |
Metode microscopice de analiza structurala
1 Microscopia Roentgen
Pentru a
obtine informatii structurale cit mai detaliate si mai profunde despre obiectele (probele) cercetate se
utilizeaza pe larg microscopia Roentgen, bazata pe difractia radiatiei
Roentgen (radiatiei X). Abaterea in cristale a unitatilor
structurale de la repartizarea lor
periodica duce la schimbarea directiei si a
intensitatii radiatiei X care, fiind inregistrata pe filmul fotografic, reda topograma obiectului de investigare.
Metodele microscopice Roentgen permit studierea atit a defectelor individuale, cit si a defectelor in ansamblu.
Ele se folosesc pe larg pentru investigarea
monocristalelor semiconductoare cu densitatea dislocatiilor relativ mica 
.1. Metoda Lang
Daca cristalul va fi supus actiunii unui fascicul de
radiatie Roentgen paralel si monocromatic de sectiune suficient
de mare astfel, incit cristalul se va afla in pozitia reflectoare, atunci 'reflexul'
va avea dimensiunile acestuia si va reda structura lui interioara.
In cazul surselor obisnuite de radiatie Roentgen si cristalelor comparativ
subtiri pentru care se respecta conditia 
unde μ este coeficientul liniar de atenuare, x - grosimea cristalului,
Lang a propus urmatorul montaj care poarta denumirea de metoda
Lang. Raza fina monocromatica de radiatie Roentgen (fig.68.) cade pe cristalul
fixat in pozitia reflectoare. Pentru obtinerea unei rezolutii
maxime in directia Bragg, care este determinata de setul lungimilor
de unda din componenta radiatiei S, se utilizeaza numai
componenta 
Separarea componentei
se realizeaza
prin instalarea in calea fasciculului primar a paravanului S1 cu o fanta
ingusta. Fanta in paravanul S2,
care serveste ca protectie pentru pelicula fotografica contra
fasciculului primar, lasa sa treaca numai fasciculul difractat.
In scopul obtinerii imaginii a intregului cristal, acestuia si
concomitent peliculei fotografice li se comunica o miscare de
du-te-vino (baleiaj) in directia paralela cu suprafata cristalului
(fig.68). Astfel se
obtine imaginea - microroentgenograma (topograma) intregului
cristal.
In cazul cind cristalul contine o imperfectiune, de exemplu dislocatia, atunci la trecerea undei prin ea va aparea un defazaj in raport cu unda ce nu intalneste imperfectiunea. Asemenea contrast de faza modifica imaginea locului respectiv pe topograma (pelicula fotografica) in raport cu alte regiuni ale cristalului.
In metoda Lang sectoarele deformate ale retelei se manifesta ca regiuni de intensitate majorata (pe pelicula fotografica regiunile de innegrire majorata).
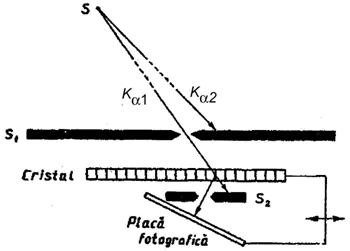
Fig.68. Metoda topografiei Roentgen dupa Lang
Majorarea intensitatii razelor reflectate de sectoarele deformate ale retelei se explica prin reducerea influentei extinctiei primare. In vecinatatea liniilor de dislocatii reteaua spatiala deformata se comporta asemanator cristalului de mozaic ideal, in care fenomenul extinctiei primare lipseste si din acest motiv razele reflectate de aceasta regiune sunt mai intense in raport cu razele reflectate de alte regiuni mai perfecte. Contrastul de acest tip se numeste contrast de extinctie.
Contrastul maxim al dislocatiilor (innegrire maxima) pe microroengenograme de difractie (topograme) se obtine la reflexie de la cele mai deformate plane, adica cind vectorul Burgers b este perpendicular pe planul reflector. In cazul acesta se respecta conditia:
(1)
unde Hhkl este vectorul retelei reciproce a planului reflector (reflexia utilizata). La reflexiile pe planele in care se afla vectorul Burgers, cind se respecta conditia
(2)
contrastul dislocatiilor nu se observa. Considerentele mentionate se folosesc la determinarea vectorului Burgers al dislocatiilor: se obtin topograme pentru citeva reflexii. Topograma cu contrastul maxim se obtine la reflexia pe planul, vectorul retelei reciproce al careia coincide cu directia vectorului Burgers.
Pentru a ne imagina aranjarea spatiala a dislocatiilor este
necesar sa se obtina topograme ale reflexiilor de tipul hkl si 
Fig. 69. Topografia siliciului deformat, obtinuta dupa
metoda lui Lang
Prin metoda Lang dislocatiile individuale pot fi evidentiate
numai in cazul cind
densitatea acestora in proba nu depaseste 
In fig.69 este prezentat un exemplu de structura cu dislocatii evidentiate prin metoda Lang. Pe topograma se observa imaginea izvorului de dislocatii (izvorul Frank-Read) in cristalul de siliciu deformat prin rasucire.
In ultimul timp la aplicarea metodei Lang in calitate de sursa se utilizeaza radiatia Roentgen sincrotrona ce contribuie la o reducere considerabila a timpului de expozitie (secunde) si permite studiul proceselor modificarii structurii reale la deformare, tranzitiilor de faza, tratarii cu radiatii, diverselor tratari tehnologice ale cristalelor.
1.2. Metoda Borrmann
Pentru studierea imperfectiunilor in cristale cu absorbtie sporita (μx>>1 unde μ este coeficientul de atenuare al radiatiei X x - grosimea cristalului) o larga utilizare a capatat una dintre cele mai sensibile metode ale microroentgenogafiei de difractie - metoda Borrmann.
Metoda Borrmann se bazeaza pe efectul de trecere anomala a fascicului monocromatic Roentgen prin cristal, daca acesta se afla in pozitia reflectoare. Efectul se explica prin faptul ca fasciculul monocromatic incident pe cristal formeaza in interiorul acestuia unde cvasistationare A si B defazate cu π (fig.70). Daca fasciculul primar So formeaza cu setul de plane (hkl) ale cristalului unghiul Bragg θ, atunci pentru una dintre unde A ventrele se vor afla intre plane (nodurile vor coincide cu planele atomice), iar pentru alta unda B ventrele vor coincide cu planele reflectoare (nodurile se vor afla intre plane). Ca rezultat va avea loc trecerea anomala a primei unde A si absorbtia puternica (anomala) a celei de-a doua unde B. Prima unda aproape ca nu se va absorbi. La o grosime suficienta a cristalului unda a doua va suferi o absorbtie completa,iarr prima unda va trece fara absorbtie. La iesirea din cristal prima unda se va diviza in doua fascicule: transmis si difractat.
Formarea in cristalul suficient de gros a doua cimpuri de unda si absorbtia unui cimp se explica prin teoria dinamica a difractiei. In cristalul subtire aceste cimpuri vor interfera si fenomenul trecerii anomale prin acesta a razelor Roentgen (efectul Borrmann) nu se va observa.
Efectul Borrmann mai poate fi explicat prin analogia cu fenomenul de canelare a particulelor. Sa ne imaginam ca cristalul este taiat dupa planul reflector astfel incit intre ambele jumatati se formeaza o fisura (fig. 71). Daca fasciculul nimereste in aceasta fisura sub unghiul Bragg, atunci in urma reflexiilor succesive pe ambele jumatati ale cristalului, care pot fi considerate niste oglinzi, fasciculul se va deplasa si va iesi in doua directii ca fascicule de intensitati egale aproape fara pierderi de energie.
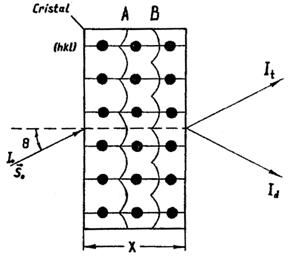
Fig. 70 Modelul fizic al efectului Borrmann
Orice distorsiuni ale retelei, care conduc la devierea elementelor acesteia in raport cu planele reflectoare, de exemplu, existenta dislocatiilor reduc efectul anomal de trecere a radiatiei Roentgen. Deci, aceste defecte se vor traduce pe microroentgenograme prin aparitia domeniilor de intensitate redusa. Existenta dislocatiilor deregleaza structura cristalina (apar extraplane) si ca urmare are loc majorarea locala a coeficientului de absorbtie. Pe microroentgenogame liniile de dislocatii se vor obtine mai luminoase in raport cu fondul.
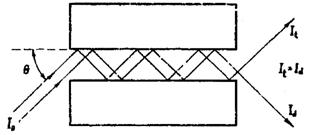
Fig. 71. Ilustratia analogiei dintre canalizarea particulei si efectul Borrmann.
In fig. 72 este prezentata schema de fotografiere prin metoda Borrmann. Proba se va fixa in pozitia reflectoare pentru planele normale la suprafata acesteia. Filmul se va instala sau distanta de la cristal sau in imediata lui suprafata. In primul caz se vor observa separat fasciculele transmise si difractate, in al doilea caz - aceste fascicule se vor suprapune. In fata filmului se poate instala un paravan astfel incit pe film se va inregistra numai fasciculul transmis.
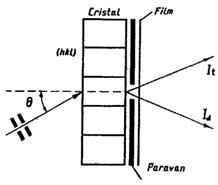
Fig.72. Metoda topografiei Roentgen dupa Borrmann
In scopul studierii intregului volum al cristalului acesta este deplasat mentinind neschimbata orientatia lui in raport cu fasciculul primar.
Efectul Borrmann este una dintre cele mai sensibile metode a microroentgenografiei de difractie si se utilizeaza pe larg la evidentierea dislocatiilor, segregatiilor si impuritatilor care distorsioneaza reteaua cristalului si creeaza domenii de inalte tensiuni locale. Gradul de relevare a dislocatiilor prin metoda Borrmann depinde atit de densitatea acestora in cristal, care nu trebuie sa depaseasca 106 cm-2, cit si de pozitia vectorului Burgers. Contrastul dislocatiilor va fi maxim atunci cind vectorul Burgers al acestora va fii perpendicular pe planul reflector. Directiile vectorului Burgers al dislocatiilor se stabilesc prin compararea microroentgenogramelor obtinute pe diferite reflexii ca si in metoda Lang.
2. MICROSCOPIA ELECTRONICA
2.1. Bazele fizice ale microscopiei electronice
In 'Microscopia optica' cea mai fina structura poate fi redata exact cu ajutorul microscopului optic numai in cazurile cind dimensiunile elementelor structurale nu depasesc marimea kλ/A, unde - lungimea de unda a radiatiei utilizate pentru iluminarea obiectului; k - constanta; A - apertura numerica a obiectivului. Din expresia pentru rezolutia limita rezulta cele doua cai de imbunatatire a acesteia: sau se micsoreaza lungimea de unda a radiatiei utilizate, sau se mareste apertura numerica. In microscopul optic rezolutia limita este de ordinul 2000 , deoarece lungimea de unda minima pentru lumina vizibila constituie aproximativ 4000 , iar apertura numerica maxima atinge valoarea 1,
In anul 1923 Louis de Broglie afirma ca orice particula in miscare are si o comportare ondulatorie. Ulterior aceasta ipoteza a fost confirmata prin numeroase experimente. S-a stabilit ca legatura dintre lungimea de unda asociata λ si impulsul p al particulei este data de relatia:
(3)
unde h - constanta lui Planck.
Pentru particulele incarcate, accelerate la o diferenta de potential U, este rational sa se exprime impulsul p prin diferenta de potential. Totodata este necesar sa se analizeze doua cazuri.
Nerelativist, cind viteza particulei incarcate v<<c (c - viteza luminii in vid). Atunci
. (4)
Daca in formula lui de Broglie constantele h, m0 si e se inlocuiesc cu valorile numerice respective pentru electron, atunci se obtine expresia:
(5)
unde λ - lungimea de unda asociata electronului in ; U - tensiunea acceleratoare in V.
(6)
Pentru electronul relativist se obtine
12,26
(7)
Factorul din parantezele rotunde reprezinta corectia relativista. Ea trebuie luata in considerare atunci cind valoarea tensiunii acceleratoare U devine apropiata de valoarea 106V.
Din formulele obtinute se vede ca lungimea de unda asociata electronului in miscare se micsoreaza cu marirea tensiunii acceleratoare. Prin urmare, capacitatea de rezolutie poate fi marita utilizind electroni accelerati pentru formarea imaginii obiectelor. Aparatele, in care se utilizeaza electronii accelerati pentru studiul structurii corpurilor, se numesc microscoape electronice. Dupa principiul de constructie si functionare ele se clasifica in citeva tipuri:
microscoape electronice de transmisie (MET);
microscoape electronice cu baleiaj (MEB);
microscoape electronice cu reflexie (MER);
microscoape electronice cu emisie (MEE).
Principalul avantaj al microscopului electronic fata de cel optic este inalta capacitate de rezolutie, in MET contemporane cu tensiunea acceleratoare de citiva MV se atinge 1.
2.2. Principiul de functionare al microscopului electronic de transmisie
Principalele parti componente ale microscopului electronic de transmisie sunt:
sistemul de iluminare;
sistemul de proiectie;
sistemul de inregistrare;
sistemul de inalta tensiune;
sistemul de vid.
In fig.73 este prezentata schema optica pentru formarea imaginii obiectului in MET cu trei trepte de marire (in regimul de observatie a microstructurii obiectului).
Proba AB, studiata in
fasciculul electronic transmis, este plasata in apropierea lentilei electromagnetice
obiectiv Imaginea marita A'B', formata de obiectiv se numeste prima imagine
intermediara. Ea, serveste in calitate de obiect pentru lentila electromagnetica
intermediara 6, care formeaza a doua imagine intermediara A'B'. Apoi imaginea A'B'
este marita de lentila electromagnetica proiector 7, care formeaza imaginea
finala 
a obiectului AB pe ecranul fluorescent sau pe placa fotografica 8.
Imaginea finala marita poate fi modificata reglind curentul lentilei intermediare sau al
lentilei proiector.
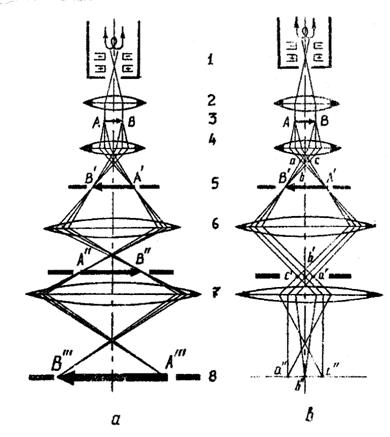
Fig.73. Schema de principiu a microscopului electronic prin transmisie: a - regim de formare a imaginii; b - regim de microdifractie; 1 - sursa de electroni; 2 - lentila-condensor;
3 - obiect; 4 - lentila-obiectiv; 5 - diafragma colectoare;
6 - lentila intermediara; 7 - lentila de proiectare;
8 - ecran fluorescent sau placa fotografica
In MET contrastul imaginii este conditionat de intensitatea undelor asociate electronilor reflectati conform legii lui Bragg, pe diferite sectoare ale probei-folie de studiu. Cu ajutorul diafragmei apertura a lentilei obiectiv electronii reflectati sunt retinuti si acestea nu participa la formarea imaginii. In acest caz imaginea este formata numai de fasciculul direct si de electronii imprastiati neelastic la unghiuri mici. Aceasta forma de reprezentare a imaginii se numeste imagine in cimp luminos,iar contrastul - prin difractie.
Daca prin inclinatia sistemului de iluminare sau prin deplasarea respectiva a diafragmei apertura,fasciculul difractat (reflectat conform legii lui Bragg) este dirijat pe axa lentilei obiectiv, atunci imaginea obiectului va fi formata de razele reflectate. Asa forma de reprezentare a imaginii se numeste imagine in cimp intunecat.
Obtinerea in MET a imaginilor in cimp luminos si in cimp intunecat se completeaza una pe alta si permite a judeca cu o mare certitudine despre microstructura obiectului studiat.
In MET poate fi obtinut tabloul de difractie de la sectoarele mici ale obiectului - microdifractograma. Pentru aceasta trebuie de micsorat puterea optica a lentilei intermediare si de facut t posibil ca planul focal posterior al lentilei obiectiv sa fiet focalizat pe ecran. In acest caz pe ecran se va observa tabloul de difractie a electronilor de la sectorul translucid al probei, plasata in planul de formare a primei imagini intermediare (vezi in fig.73 mersul razelor in MET in regimul microdifractiei).
Obtinind microdifractograma, se poate de legat particularitatile structurii probei, evidentiate pe microfotografie, cu cristalografia acesteia. Afara de aceasta, microdifractograma poate fi utilizata pentru identificarea fazelor in proba cu structura eterogena.
Principiul de functionare al microscopului electronic cu baleiaj
La interactiunea fasciculului de electroni cu proba - tinta apar numeroase efecte fizice care servesc ca surse de diverse tipuri de semnale. La ele se refera radiatia X, catodoluminiscenta, electronii reflectati, absorbiti, secundari, transmisi si Auger, curentul indus de sonda electronica si tensiunea electromotoare indusa de sarcina.
Semnalele formate de detectoarele respective se amplifica si se utilizeaza la dirijarea stralucirii ecranului tubului catodic (TC). Pentru fiecare punct al probei exista un punct pe ecranull TC stralucirea caruia este conditionata de semnalul detectorului obtinut ca rezultat al interactiei sondei electronice cu proba.
Daca interactia ar fi aceeasi in toate punctele probei, atunci pe ecranul TC ar fi o stralucire uniforma, in realitate, din cauza variatiei proprietatilor locale ale probei, interactia fasciculului electronic in diferite locuri ale probei este diferita.
Daca in doua puncte P1 si P2 semnalul S este diferit dupa valoare, atunci spunem ca exista contrast intre imaginile acestor puncte, iar masura contrastului este marimea
unde S1 si S2 sunt semnalele in punctele 1 si 2; Smed este nivelul semnalului mediat pentru toate punctele.
Asupra caracterului de interactie al fascicului cu proba pot influenta topografia, componenta chimica, structura cristalina, cimpul electric si magnetic si alte proprietati ale probei. Deoarece caracterul de interactie variaza de la un punct la alt punct al suprafetei probei semnalele formate de detectori, prin urmare si stralucirea punctelor respective pe ecranul TC, de asemenea vor varia. Asupra formarii imaginii influenteaza fiecare semnal de interactie al electronilor cu proba. Aceste semnale in microscopia electronica cu baleiaj se utilizeaza pentru obtinerea informatiei despre componenta calitativa si cantitativa a substantei, despre proprietatile fizice, fizico - chimice si cristalochimice ale acesteia. Unele semnale (emisia electronica secundara, catodoluminiscenta, curentul indus de sonda electronica) se utilizeaza pentru studiul dispozitivelor cu semiconductori in regimurile static si dinamic.
Principiul de functionare a MEB este prezentat in schema - bloc din fig.7 Fasciculul de electroni este format de tunul electronic 1. La iesirea din tunul electronic diametrul minim al fasciculului, in cazul utilizarii catodului de volfram de forma sagetii (termoemitor), constituie aproximativ 10 μm, iar in cazul utilizarii emiterului autoelectronic (de forma unui ac) - mai putin de 10 μm. Apoi fasciculul electronic cu energia in intervalul 0,1 - 50 keV (in dependenta de tensiunea acceleratoare) este focalizat cu una dintre cele doua lentile condensor 2, este deflectat in rastru cu ajutorul a doua perechi de bobine deviatoare 3, prin care de la un generator 4 se avanseaza curent in forma de dinti de ferestrau si in cele din urma este focalizat in forma de sonda de diametru mic (de obicei mai mic de 10 nm) pe proba 6 de catre lentila obiectiv 5. Imaginea obiectului va fi obtinuta in regimul electronilor secundari 7 sau cu ajutorul electronilor incidenti reflectati 8.
Electronii secundari smulsi din proba sau electronii incidenti reflectati nimeresc in cimpul electric al colectorilor 13 si 14 respectiv si sunt captati de acestia. Fiind amplificat de amplificatorul 21, videosemnalul este avansat la modulatorul TC 22 cu o deflectare sincrona a fasciculului de catre bobinele deviatoare 3 alimentate cu curent de la generatorul
Semnalul video in prealabil (pina la avansarea la TC) poate fi prelucrat de un dispozitiv videocontrol al MEB pentru majorarea raportului semnal/zgomot al contrastului imaginii, inregistrarea cadrului etc. In MEB moderne dirijarea fasciculului se realizeaza cu ajutorul computerului. Sonda electronica, fiind fixata pe o durata mica de timp, pe o regiune mica a suprafetei probei, prin salt este deplasata pe o alta regiune.
Particularitatea caracteristica a imaginilor obtinute in MEB, in comparatie cu cele optice, este marea adincime a claritatii: aproximativ cu doua ordine de marime mai mare decit intr-un microscop optic obisnuit. Acest efect 'pozitiv' este conditionat de cel 'negativ' - de marea aberatie sferica a lentilelor electromagnetice, care micsoreaza apertura unghiulara a fasciculului electronic.
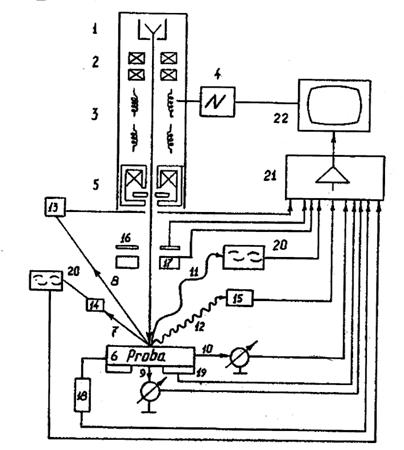
Fig.7 Schema-bloc a coloanei si formarea imaginii in MEB:
1 - tun electronic; 2 - lentile-condensor; 3 - bobine deviatoare;
4 - generator de deflectare; 5 - lentila-obiectiv; 6 - proba;
7 - electroni secundari; 8 - electroni primari reflectati;
9 - electroni transmisi; 10 - electroni absorbiti; 11 - luminiscenta catodica; 12 - radiatie X; 13,14,15 - detectori de electroni secundari, primari reflectati si de radiatie X; 16 - detector de TEM indusa de sarcina; 17 - rezonator de ultrainalta frecventa; 18 - inregistrator DLTS; 19 - piezotransformator; 20 - fotomultiplicator; 21 - videoamplificator;
22 - tub catodic
Formarea imaginii in MEB 'punct cu punct' (dimensiunea 'punctului' aproximativ corespunde diametrului sondei electronice pe proba) esential simplifica interpretarea imaginilor obtinute in acesta fata de cele obtinute in MET, care se formeaza, practic, in acelasi moment cu interferenta fasciculelor electronice, transmise prin diferite 'puncte' ale probei. Transformarea informatiei despre starea suprafetei probei in cod temporal permite utilizarea diverselor metode radiotehnice la prelucrarea videosemnalului: de a ingusta sau a largi banda de transmisiune, de a imbunatati raportul semnal/zgomot, de a realiza transformarea neliniara a semnalului (asa-numita corectia - Y) pentru imbunatatirea contrastului imaginii etc.
Datorita acestor particularitati de obtinere a videosemnalului si de formare a imaginii MEB au o larga utilizare in diverse domenii ale stiintei si tehnicii contemporane.
Una dintre importantele performante ale MEB reprezinta numeroasele moduri de obtinere a informatiei despre proba, fiind rezultatul varietatilor mecanismelor fizice de interactie a fasciculului electronic cu corpul solid (fig.74).
3. MICROSCOPIA TUNEL CU BALEIAJ
Microscopia tunel cu baleiaj (MTB) a fost fondata in anul 1981 de catre laureatii premiului Nobel G. Binnig si G. Rohrer. Ea ofera posibilitatea de a analiza atom cu atom, adica de a traversa periodic rind cu rind intregul sector supus examinarii al obiectului de studiu. Astfel s-au realizat progrese in vederea cunoasterii lumii atomilor separati in orice substanta fara a o distruge.
Principiul de functionare al MTB comparativ este simplu: catre suprafata de studiu se apropie un ac pina cind intre proba si ac nu se va crea un curent de tunel (fig. 75). Cu ajutorul computerului se dirijeaza deplasarea acului, mentinindu-se constanta distanta ac - proba sau curentul de tunel. Raza de curbura a virfului ascutit (de obicei din volfram) este mai mica de 1000 , spatiul de lucru (de la virful acului pina la suprafata examinata a probei) este de circa 3 , tensiunea de lucru intre ac si proba este aproximativ de 0,1 10 V, curentul de tunel, de obicei, se afla in limitele 0,1 10 nA si variaza aproximativ cu ordinul de marime la variatia spatiului de lucru cu 1 .
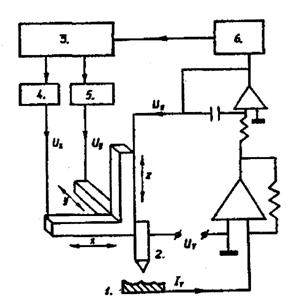
Fig.75. Schema-bloc a MTB: 1 - proba; 2 - ac; 3 - computer; 4, 5, 6 - convertizoare analoge-digitale
Curentul de tunel in fond 'cordona' intre cei mai apropiati atomi ai acului si probei, fapt ce conduce la o rezolutie a MTB 'pe orizontala' (in planul suprafetei examinate)de ordinull dimensiunilor atomice - circa 1 . Datorita dependentei exponentiale a probabilitatii de tunelare de distanta ac-proba r
(8)
unde m0 - masa electronului; 
- constanta lui
Planck; U - inaltimea barierei de potential, rezolutia MTB 'pe
verticala' atinge 10-2 . Deci, cu ajutorul acestui aparat
se poate localiza un volum de aproximativ
Inventarea microscopului tunel cu baleiaj a largit esential limitele de utilizare a microscopiei cu baleiaj. Din punctul de vedere al aplicatiilor in domeniul fizicii corpului solid si al microelectronicii cu semiconductori MTB prezinta interes prin faptul ca poseda un inalt grad de rezolutie (pina la 1 ) si poate functiona atit in vid cit si in medii lichide si gazoase, inclusiv poate servi drept sursa de informatie despre microrelieful suprafetei examinate, spectrele starilorr electronice, investigarea proceselor de crestere a peliculelor si de generare a defectelor etc. Acest aparat poate fi combinat cu MEB astfel incit ambele se completeaza unul pe altul. Daca MTB se utilizeaza nu in regimul curentului de tunel, ci in regimul emisiei autoelectronice, atunci acesta poate fi transformat intr-un analog al MEB cu energii mici ale fasciculului: la energia de 15 eV rezolutia unui astfel de 'MEB fara lentile' este aproximativ de 30 . Pot fi studiate de asemenea oscilatiile curentului ce apar in spatiul ac-proba, fiind similare cu undele electronice stationare, emisia fotonilor, mecanismele de excitare ale plasmonilor etc.
MTB face posibila trasarea desenelor in diapazonul de dimensiuni nanometrice, adica crearea nanotehnologiei.
Microscopia de forta atomica
O varietate a MTB prezinta microscopul de forta atomica (MFA). Acesta inregistreaza forte de interactiune Van der Waals foarte mici (mai mici de 1nN) intre ac si proba. Aceste forte descresc cu distanta r proportional cu r-8 (pentru doi atomi separati). Rezolutiile MFA si MTB sunt de acelasi ordin de marime. Principiul de functionare a MFA este ilustrat in fig.76: devierea microresortului (microconsolei) pe care este fixat acul-detector al interactiunii de forta (aici - granula de diamant), este controlata dupa curentul de tunel intre cel de-al doilea ac si partea opusa a microresortului (adica regimul obisnuit de functionare a MFA). Pentru controlul pozitiei microresortului se mai utilizeaza metodele interferometriei laser si inregistrarea variatiilor capacitatii. Microresorturile, in majoritatea cazurilor, sunt confectionate dintr-un strat de SiO2 pe Si prin metoda microtehnologiei care asigura o rezolutie mai buna de 2,5 .
Spre deosebire de MTB, cu ajutorul caruia pot fi studiate numai probe cu conductivitate sporita, MFA ofera posibilitatea de a studia si obiecte dielectrice. Daca acul-detector de forta este confectionat dintr-un material feromagnetic, atunci MFA permite a studia si structura magnetica a probelor, in special a peretilor de domenii. Deosebirea fundamentala de principiu dintre MTB si MFA consta in aceea ca MTB reda convolutia electronica si topografica a structurii probei, iar MFA - o oarecare suma de pozitii ale atomilor, legaturilor acestora si interactiunii cu acul de baleiaj.
Afara de MFA deja sunt elaborate si alte varietati ale MTB: aparate cu surse ionice, ascutisul carora este confectionat din metal lichid, cu micropipete de baleiaj, cu inregistrarea undelor termice etc., rezolutia carora este apropiata de rezolutia MTB. MTB si MFA se utilizeaza la studiul undelor densitatii de sarcina in cristale, structuriii supraconductorilor, la detectarea frecventelor optice tinind contt de caracterul neliniar al caracteristicii tensiune-curent a contactului ascutis-suprafata de examinare, la inregistrarea diferitelor radiatii (spectroscopia izocromatica, fluorescenta si luminiscenta).
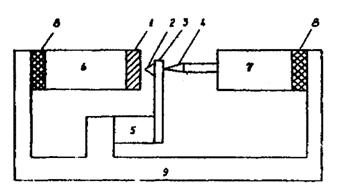
Fig.76. Schema microscopului de forta atomica: 1 - proba; 2 - ascutisul MFA; 3 - microresort sensibil; 4 - ascutisul MTB pentru controlul pozitiei microresortului; 5 - piezoelement pentru punerea in functiune a ascutisului MFA; 6, 7 - piezoanalizoare ale MFA si MTB; 8 - garnitura amortizor; 9 - carcasa de aluminiu
MTB se combina cu MEB si cu alte aparate si instalatii de supravid, cu microscoape ionice cu efect de cimp, cu microscoape de reflexie, cu instalatii pentru difractia electronilor lenti etc. MFA poate fi utilizat la studiul proprietatilor de suprafata ale structurilor dielectrice si la masurarea potentialelor. Sensibilitatea accesibila la masurarea capacitatilor este de 10-22 F. Se disting incluziuni ale dielectricului pe substratul de siliciu si se masoara distributia potentialelor pe jonctiunea p-n cu o rezolutie submicronica. Se detecteaza pina si salturile de potential de ordinul 1 μV conditionate de electronii imprastiati la granitele granulelor.
Inventarea microscopului tunel cu baleiaj a deschis o noua etapa in dezvoltarea stiintei pe scara mondiala. Au luat nastere cele mai moderne ramuri ale stiintelor tehnologice si mai intii de toate nanotehnologia, care ofera posibilitatea de a elabora instalatii nanotehnologice si de a incepe crearea din atomi separati a unor structuri cu multi atomi, care este imposibil sa fie obtinute prin metode microtehnologice. Au fost create primele nanoscoape, care ofera posibilitatea de a vedea si a intelege fenomene necunoscute pina in prezent. Au fost puse bazele nanoelectronicii.
BIBLIOGRAFIE
Iuliu Pop, Mircea Crisan. Fizica corpului solid si a se mi con ductorilor. Editura Didactica si Pedagocica, Bucuresti 1983.
B.K. Vainstein. Cristalografia moderna. Vol 1. Editura Stiintifica si Enciclopedica, Bucuresti 1989.
Kittel Ch. Introducere in fizica corpului solid. Editura Tehnica, Bucuresti 1972.
C. Pumnea, I. Dina, Fl. Sarescu, M. Dumitru, I. Niculescu. Tehnici speciale de analiza fizico-chimica a materialelor metalice. Editura tehnica, Bucuresti 1988.
I. Sirotin, M. Sascolskaia. Fizica cristalelor. Editura tehnica, Bucuresti 1981.
C. Gheorghies. Controlul structurii fine a metalelor cu radiatii X. Editura tehnica, Bucuresti 1990.
C. Gheorghies, L. Gheorghies. Controlul texturii metalelor cu radiatii X. Editura tehnica, Bucuresti 199
C. Gheorghies, L. Gheorghies, R. Chirila. Rntgenocristalografie. Culegere de probleme. Editura tehnica, Bucuresti 199
I. Samusi, N. Burbulea, M. Nazarov. Metode Microscopice de analiza structurala. Chisinau U.T.M. 1996.
I. Samusi, M. Rusanovschi. Practicum de analiza structurala. Chisinau U.T.M. 1993.
M
Рентгенография кристаллов. Теория и практика. М., Физматгиз, 1961.
Мир, 1978.
N
N
|
Politica de confidentialitate | Termeni si conditii de utilizare |
Vizualizari: 3044
Importanta: 
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved
