| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Oscilatiile punctului material
1. Miscarea oscilatorie
2. Factori care determina miscarea oscilatorie
3. Ecuatia miscarii oscilatorii armonice
4. Marimi caracteristice miscarii de oscilatie
5. Viteza si acceleratia an miscarea oscilatorie armonica
Energia oscilatorului armonic
7. Oscilatii amortizate
8. Oscilatii fortate (intretinute). Rezonanta
9. Compunerea oscilatiilor
1. Miscarea oscilatorie
In natura si tehnica se intalnesc procese repetabile in timp care stau la baza oscilatiilor de diferite feluri.
 Caracteristici ale miscarii oscilatorii:
Caracteristici ale miscarii oscilatorii:
Existenta unei pozitii de echilibru
Miscarea se efectueaza in ambele sensuri, in jurul pozitiei de echilibru.
Traiectoria miscarii are doua extreme.
In aceste pozitii extreme viteza corpurilor este nula.
Fig. 5.1 Exemple de miscari periodice.
Definitie: Un corp solid sau lichid care se misca in ambele sensuri pe aceeasi traiectorie, executa o miscare de oscilatie mecanica.
Definitie: Miscarea unui corp care se repeta la intervale egale de timp si se executa simetric fata de pozitia de echilibru se numeste miscare oscilatorie periodica.
Definitie: Sistemele care efectueaza miscarile descrise mai sus se numesc oscilatori.
2. Factori care determina miscarea oscilatorie
Energia initiala suplimentara, care este necesara pentru scoaterea corpului din pozitia de echilibru reprezinta primul factor care determina miscarea de oscilatie. Forta care actioneaza asupra unui corp si este mereu indreptata spre pozitia de echilibru se numeste forta elastica de revenire si este al doilea factor care determina o miscare oscilatorie.

![]()
unde k este o constanta care caracterizeza
sistemul oscilator; iar x este departarea cor-
pului fata de pozitia de echilibru si se nu-
meste elongatie. Daca asupra corpului care
executa o miscare de oscilatie actioneaza
numai o forta de tip elastic atunci aceasta
miscare ideala este numita armonica.
Fig. 5.2 Impulsul initial si apoi
forta de revenire conduc la apari-
tia unei miscari oscilatorii.
3. Ecuatia miscarii oscilatorii armonice
Energia potentiala este minima in pozitia de echilibru. Daca notam cu Wp(x) energia potentiala atunci aceasta se poate dezvolta in serie Taylor in jurul pozitiei de echilibru:
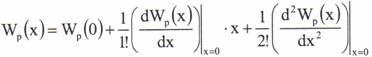

 Consideram oscilatii mici in jurul
pozitiei de e-
Consideram oscilatii mici in jurul
pozitiei de e-
chilibru, x = 0. Derivata I-a este zero in aceasta
pozitie de echilibru iar energia potentiala in x=0
este o constanta pe care o putem considera zero,
Wp

Fig. 5.3 Energia potentiala poate
fi in general o curba oarecare
aproximata in jurul lui x = o
de o parabola.
expresia energiei potentiale devine:

unde k este considerata constanta elastica. Daca campul este conservativ atunci Forta deriva dintr-un potential (energia potentiala):

care este o forta de tip elastic. Conditia a II-a pentru producerea unei miscari oscilatorii.
Daca tinem cont de legea a doua a lui Newton se poate obtine ecuatia de miscare:
![]()
care prin impartirea cu masa corpului, ne da:

unde s-a notat:
![]()
Se face urmatoarea conventie in notatii:

atunci ecuatia de miscare devine:
![]()
care este o ecuatie diferentiala liniara de ordinul doi cu coeficienti constanti. Solutia generala este de forma:
![]()
sau sub forma:
![]()
unde C si C sunt doua constante de integrare. Putem introduce alte doua constante A (amplitudinea) si φ (faza). Atunci ecuatia de miscare se poate scrie ca:
![]()

care este ecuatia miscarii oscilatorii
armonice.

de unde prin identificarea coeficientilor
Fig. 5.4 Reprezentarea grafica a elon- din ecuatia (5.13) cu ecuatia (5.15) ob-
gatiei din ecuatia 5.14 in functie de tinem:
timp

 de unde:
de unde:
4. Marimi caracteristice miscarii de oscilatie
Miscarea de oscilatie este caracterizata de departarea momentana sau elongatie x(t).
Definitie: Elongatia x indica departarea corpului la un moment dat fata de pozitia de echilibru.
Definitie: Deviatia maxima a corpului fata de pozitia de echilibru se numeste amplitudine.
Amplitudinea, A este intotdeauna pozitiva.
Faza miscarii φ(t) = ω ∙ t + φ - indica starea si sensul miscarii la un moment dat. Faza initiala este φ . Iar ω se numeste pulsatie si are dimensiunea unei viteze unghiulare.
Definitie: Marimea T care caracterizeaza periodicitatea miscarii de oscilatie se numeste perioada a oscilatiei.
Definitie: Perioada de oscilatie, T este timpul necesar pentru efectuarea unei oscilatii complete.
Definitie: Frecventa de oscilatie v reprezinta numarul de oscilatii efectuate in unitatea de timp.

deci intre frecventa si perioada exista relatia:

unitatea de masura pentru frecventa este:

si daca tinem cont si de ecuatia (5.9) obtinem perioada de oscilatie:

5. Viteza si acceleratia in miscarea oscilatorie armonica
Viteza unui punct material aflat in miscare oscilatorie este data de:
![]()
![]() Acceleratia unui punct material
aflat in miscare oscilatorie este data de:
Acceleratia unui punct material
aflat in miscare oscilatorie este data de:
sau daca introducem expresia elongatiei obtinem:
![]()
Energia oscilatorului armonic
Sa consideram un oscilator ideal. In acest caz energia totala se conserva. Ea este compusa din energie cinetica si energie potentiala de deformare.
![]()
unde:
Energia potentiala este:

![]()
Energia cinetica este:
![]()
![]()
Energia totala data de ecuatia (5.25) devine:
![]()
7. Oscilatii amortizate
In orice problema reala intervin insa forte de rezistenta din partea mediului, din partea legaturilor, care conduc la o disipare in timp a energiei sistemului fapt care conduce la amortizarea oscilatiilor. Sa consideram un corp care se misca cu viteza proportionala cu viteza acestuia:
![]()
Ecuatia de miscare a punctului material:
![]()
Introducand notatiile:

de unde ecuatia de miscare este:
![]()
care este o ecuatie diferentiala, omogena, de gradul al doilea cu coeficienti constanti. Ecuatia caracteristica este:
![]()
care are solutia:
![]()
de unde solutia generala a ecuatiei (5.32) este:
![]()

Daca forta de frecare este foarte mare δ > ω atunci constantele λ si λ sunt reale, si nu se mai produce nici o miscare oscilatorie, amplitudinea scazand exponential in timp. Daca forta de frecare este mai mica δ < ω solutiile sunt marimi complexe, iar in acest caz miscarea este periodica. Daca notam:
![]()
atunci ecuatia de miscare devine:
![]()
care poate fi rescrisa folosindu-se functiile armonice, sinus si cosinus:
![]()
![]()
sau trecand sub forma cunoscuta:

![]()
unde se observa ca amplitudinea se
modifica in timp dupa ecuatia:
![]()
Perioada acestei miscari este:

Fig. 5.5 Reprezentarea grafica a elongatiei
din ecuatia 5.39 in functie de timp. Ampli-
tudinea este si ea o functie de timp data de 5.40.
Caracteristicile oscilatiilor amortizate:
Decrementul logaritmic al amortizarii:
![]()

![]() Timpul de relaxare
- este
timpul in care amplitudinea scade de e ori:
Timpul de relaxare
- este
timpul in care amplitudinea scade de e ori:
de unde:
![]()
iar timpul de relaxare, τ este:

Atenuarea este:
![]()
care este pozitiva (Q>0) pentru o miscare periodica si este negativa (Q<0) pentru o miscare aperiodica.
8. Oscilatii fortate (intretinute). Rezonanta
Pentru a mentine o miscare oscilatorie cu amplitudine constanta, in cazul prezentei fortelor de frecare, este nevoie sa se transmita periodic energie sistemului sub forma unei forte care sa compenseze amortizarea. Ea este de forma:
![]()
miscarea punctului material este descrisa de ecuatia:
![]()
sau:

solutia acestei ecuatii diferentiale este suma a doua solutii i) a ecuatiei omogene si ii) de forma membrului drept:
![]()
unde:
![]()
si:
![]()
pentru un timp suficient de lung avem ca si solutie doar cea de forma termenului drept, pentru ca solutia ecuatiei omogene tinde la zero:
![]()
viteza este:
![]()
iar acceleratia este:
![]()
ecuatia de miscare devine:
![]()
![]()
prin dezvoltarea functiilor sinus si cosinus si identificarea coeficientilor obtinem:

de unde amplitudinea A si faza φ sunt:

Amplitudinea miscarii atinge o valoare maxima pentru pulsatia care respecta conditia:
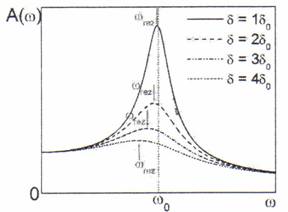

de unde:

care este adevarat pentru ω = 0
adica in absenta fortei perturba-
toare sau pentru:

Fig. 5.6 Amplitudinea oscilatiilor
fortate in functie de pulsatia
acestora pentru diferite valori δ.
care este frecventa de rezonanta. Amplitudinea devine maxima avand valoarea:

9. Compunerea oscilatiilor
De cele mai multe ori corpurile nu sunt supuse unei singure forte si care sa aiba ca efect o miscare oscilatorie pura, fie aceasta amortizata sau fortata, avand astfel o miscare mult mai complexa. Cand fortele care actioneaza asupra corpurilor sunt de tip elastic miscarea rezultata poate fi descrisa prin suprapunerea miscarilor oscilatorii datorate fiecarei forte. Acest lucru se numeste, pe scurt, compunerea oscilatiilor. Exista cateva cazuri particulare care la o privire mai atenta pot sta la baza oricarei compuneri arbitrarii a oscilatiilor. Aceste cazuri depind de directiile de oscilatie relative a doua miscari oscilatorii, si anume oscilatii paralele si oscilatii perpendiculare, sau pot sa depinda de frecventa acestor oscilatii, conducand la oscilatii de aceeasi frecventa si de frecvente diferite.
Compunerea oscilatiilor paralele de frecvente egale
Sa consideram un punct din spatiu, P in care se suprapun doua oscilatii armonice paralele, de aceeasi frecventa, v descrise de ecuatiile de miscare:

 unde y , A sunt elongatia, am-
unde y , A sunt elongatia, am-
plitudinea si respectiv faza initiala
a miscarii oscilatorii a punctului P
in absenta celei de-a doua oscilatii
iar y , A sunt elongatia, ampli-
tudinea si respectiv faza initiala a
miscarii oscilatorii a punctului P in
absenta primei oscilatii.
Fig. 5.7 Diagrama fazoriala a compunerii Miscarea compusa rezultata este:
oscilatiilor paralele de aceeasi frecventa.
![]()
![]()
este tot o miscare oscilatorie descrisa de ecuatia:
![]()
Tot ce avem acum de facut este sa determinam componentele miscarii rezultate, si anume amplitudinea A , si faza initiala, φ a miscarii. Pentru aceasta, cel mai usor este sa consideram diagrama fazoriala a miscarii, unde miscarea oscilatorie este considerata ca o proiectie pe o axa, in cazul de fata y a unei miscari circulare cu raza egala cu amplitudinea, viteza circulara data de pulsatie iar faza initiala fiind chiar unghiul initial. Amplitudinea se poate calcula usor folosind teorema lui Pitagora generalizata:
![]()
iar:

faza initiala a acesteia.
Exista doua cazuri particulare interesante care merita mentionate. Primul este acela cand miscarile sunt in faza (φ = 0), iar amplitudinea este maxima:
![]()
si al doilea caz in care cele doua miscari sunt in antifaza φ = π), iar amplitudinea este minima:
![]()
Compunerea oscilatiilor paralele de amplitudini egale si fecvente diferite
Sa consideram un punct din spatiu, P in care se suprapun doua oscilatii armonice paralele, de aceeasi amplitudine, A si frecvente diferite descrise de ecuatiile de miscare:

Ecuatia de miscare rezultata este data de suma ecuatiilor individuale:
![]()
![]()
este tot o miscare oscilatorie. Daca se foloseste o binecunoscuta formula trigonometrica:
![]()
ecuatia de miscare devine:


si care se mai poate rescrie:


 care este ecuatia unei
miscari oscilatorii cu amplitudinea rezultata dependenta de timp:
care este ecuatia unei
miscari oscilatorii cu amplitudinea rezultata dependenta de timp:
![]()
 si pulsatia
determinata de media pul-
si pulsatia
determinata de media pul-
satiilor celor doua oscilatii individu-
 ale:
ale:
Pentru usurinta, fara a schimba sen-
sul celor ce urmeaza se pot conside-
ra fazele initiale a celor doua mis-
cari ca fiind zero:
![]()
Fig. 5.8 Compunerea a doua oscilatii paralele cu amplitudini constante si de frecvente diferite conduce la aparitia unei oscilatii cu amplitudinea modulata cunoscut ca fenomen fizic numit batai.
iar ecuatia de miscare devine
![]()
Se observa ca in cazul in care cele 2 oscilatii au aceeasi pulsatie se obtine rezultatul discutat la punctul anterior:
![]()
In cazul general in care pulsatiile celor 2 oscilatii difera ω amplitudinea rezultata trece prin maxime si minime la diferite momente de timp. Astfel fenomenul de variatie periodica a amplitudinii oscilatiei rezultante poarta numele de batai.
Compunerea oscilatiilor perpendiculare de frecventa egala dar amplitudini diferite
Daca consideram un punct P care efectueaza oscilatii sub actiunea simultana a doua forte elastice perpendiculare. Ecuatiile de miscare care descriu acum miscarea corpului sunt date de expresiile:

unde A si B sunt amplitudinile celor 2 miscari oscilatorii perpendiculare cu fazele, φx si φy. In acest caz scopul nu-l mai reprezinta determinarea ecuatiei de miscare, deoarece acestea sunt deja date de ecuatia (5.77) ci determinarea traiectoriei punctului material in planul XOY. Pentru aceasta se impart cele doua ecuatii la amplitudinile corespunzatoare:




de unde in final se obtine ecuatia generala a unei elipse:
![]()
Daca se compun doua oscilatii perpendiculare cu frecventele care satisfac relatiile v / v = N / N cu N si N doua numere naturale, atunci prin suprapunere iau nastere asa numitele figuri Lissajous.


Fig. 5.9 Figurile Lissajous, obtinute din ecuatia 5.80 si reprezinta compunerea a doua oscilatii perpendiculare cu amplitudini diferite si raportul frecventelor dat de raportul a doua numere intregi.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3947
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved