| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
CUADRICE. SUPRAFETE RIGLATE. SUPRAFETE DE ROTATIE.
1. Cuadrice de ecuatii reduse. Simetriile lor.
Gasirea formei lor geometrice prin metoda intersectiei
Ecuatiile reduse ale cuadricelor
Definitia cuadricelor si unele probleme care se pun in legatura cu ele sunt analoge cu cele de la conice
Definitia 1 Se numeste cuadrica sau suprafata de ordinul doi nucleul unei forme patratice afine pe spatiul punctual euclidian E3.
Daca o forma patratica f este data prin functia polinomiala f, atunci ecuatia generala a cuadricei S=ker f este:
S : a11x2+a22y2+a33z2+2(a12xy+a13xz+a23yz)+2(a10x+a20y+a30z)+a00=0 (1)
unde aij=aji, i,j=0,1,2,3,.
Ecuatia (1) o vom scrie uneori prescurtat:
S: f(x,y,z)=0
Matricele asociate lui f se pot scrie usor folosind semiderivatele sale partiale:
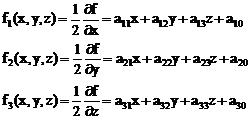 (2)
(2)
si functia: f0 (x,y,z)=a01x+a02y+a03z+a00
Matricea A se formeaza cu coeficientii coordonatelor (x,y,z) din sistemul de functii (f1,f2,f3) iar D este matricea tuturor coeficientilor sistemului de functii (f1,f2,f3,f0).
S-a demonstrat in capitolul 9 ca se poate alege un reper canonic astfel incat, ca si in cazul conicelor, ecuatia cuadricei S=ker f sa se scrie sub forma canonica, adica sub una din formele:
a) l x2+l y2+l z2=0 daca rang D=rang A; (3)
b) l x2+l y2+l z2+a a 0 daca rang D=1+rang A; (4)
c) l 1x2+l y2+2z =0, daca rang D=2+rang A .(5)
Mai mult, prin inmultirea acesteia cu un factor nenul este posibil ca ecuatia cuadricei sa se scrie sub una din formele urmatoare, numita ecuatia redusa:
1)
![]() sfera (6)
sfera (6)
2)
![]() elipsoid vid sau
imaginar ( (7)
elipsoid vid sau
imaginar ( (7)
3)
![]() elipsoid (8)
elipsoid (8)
4)
![]() hiperboloid cu o panza (9)
hiperboloid cu o panza (9)
5)
![]() hiperboloid cu doua
panze (10)
hiperboloid cu doua
panze (10)
6)
![]() paraboloid eliptic (11)
paraboloid eliptic (11)
7)
![]() paraboloid hiperbolic (12)
paraboloid hiperbolic (12)
8)
![]() cuadrica nula sau
punct dublu (13)
cuadrica nula sau
punct dublu (13)
9)
![]() con patratic sau
suprafata conica de gradul 2 (14)
con patratic sau
suprafata conica de gradul 2 (14)
10)
![]() cilindru vid sau
imaginar ( (15)
cilindru vid sau
imaginar ( (15)
11)
![]() cilindru eliptic (16)
cilindru eliptic (16)
12)
![]() cilindru hiperbolic (17)
cilindru hiperbolic (17)
13) x2-2y=0 cilindru parabolic (18)
14)
![]() dreapta dubla (19)
dreapta dubla (19)
15)
![]() pereche de plane
secante (20)
pereche de plane
secante (20)
16)
![]() pereche de plane
strict paralele (21)
pereche de plane
strict paralele (21)
17)
![]() pereche vida de plane
paralele ( (22)
pereche vida de plane
paralele ( (22)
18)
![]() plan dublu (23)
plan dublu (23)
Cuadricele se impart in doua mari clase: cuadrice propriu zise (nesingulare) si cuadrice singulare (degenerate ). Cuadrcele 6-12 sunt cuadrice propriu zise, iar cuadricele 13-23 sunt cuadrice singulare.
Forma geometrica a cuadricelor
Vom prezenta imaginea geometrica a cuadricelor si vom justifica faptul
ca acestea sunt intr-adevar imaginile lor prin metoda intersectiilor.
Elipsoidul (fig 1) dat prin ecuatia redusa (8) sectionat cu planul z=k (k=constant) determina conica:
![]() (24)
(24)
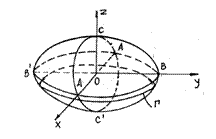 care
este elipsa pentru k2<c2, elipsa vida pentru k2>c2
si punct dublu pentru k2=c2.
care
este elipsa pentru k2<c2, elipsa vida pentru k2>c2
si punct dublu pentru k2=c2.
Fig.1
Se poate arata ca prin intersectia cu oricare alt plan conica obtinuta este o elipsa, elipsa vida sau punct dublu. Elipsoidul poate fi generat de elipsa mobila G care sprijina pe elipsa fixa ACA'C cand planul XOZ se deplaseaza paralel cu el insusi.
Ecuatia carteziana implicita a elipsoidului:
![]()
este echivalenta cu ecuatiile parametrice:
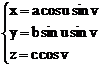 (25)
(25)
![]() u,v= parametri (fig 2) pe suprafata.
u,v= parametri (fig 2) pe suprafata.
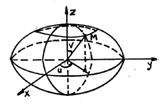
Fig.2
Daca a=b c ecuatia elipsoidului este:
![]() (26)
(26)
Elipsoidul dat de (26) este de rotatie in jurul lui Oz. Daca a=b=c ecuatia (26) devine x2+y2+z2=a2 (sfera de raza a cu centrul in O).
Hipeboloidul cu o panza (9) dat prin ecuatia redusa 4), sectionat cu un plan z=k determina elipsa:
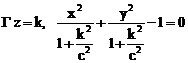 (27)
(27)
sectionat cu un plan y=h determina conica:
y=h, ![]() (28)
(28)
care este hiperbola pentru h2 b2 si pereche de drepte scante pentru h2=b2. Se poate arata ca prin intersectia cu oricare alt plan, conica obtinuta este elipsa, hiperbola sau pereche de drepte secante.
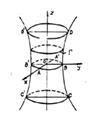
Fig.3
Ecuatiile parametrice ale hiperboloidului cu o panza (12.9) sunt:
![]() (29)
(29)
Aceasta cuadrica poate fi generata de elipsa G care se sprijina pe hiperbola fixa CC'DD' cand planul xOy se deplaseaza paralel cu el insusi.
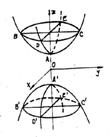
Hiperboloidul cu doua panze (fig.4) dat prin ecuatia redusa 10), sectionat cu planul x=k determina hiperbola:
G
: x=k, ![]() (30)
(30)
Sectionat cu planul z=h determina conica:
z=h,
![]() (31)
(31)
care este elipsa pentru
![]() , elipsa vida pentru
, elipsa vida pentru ![]() si punct dublu pentru
si punct dublu pentru ![]() . Conica obtinuta cu oricare alt plan de sectiune este
hiperbola, elipsa sau elipsa vida.
. Conica obtinuta cu oricare alt plan de sectiune este
hiperbola, elipsa sau elipsa vida.
Fig.4
O reprezentare parametrica a hiperboloidului cu doua panze:
![]()
este
![]() , u,v= parametrii
(32)
, u,v= parametrii
(32)
Aceasta cuadrica poate fi generata de hiperbola G (30) care se sprijina pe hiperbola DAEDA'E' (fig 4).
Paraboloidul eliptic (fig 5) dat prin ecuatia redusa 11), sectionat cu planul x=k, determina parabola:
G:x=k, ![]() (33)
(33)
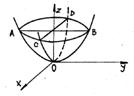
Fig 5
Sectionat cu planul z=h, determina conica:
G :
z=h, ![]() (34)
(34)
care este elipsa daca h>0, elipsa vida daca h<0 si un punct dublu daca h=0.
Conica obtinuta prin sectionarea cu oricare alt plan este elipsa vida, punct dublu sau parabola.
Paraboloidul eliptic de ecuatie:
![]()
are urmatoarele ecuatii parametrice
![]() (35)
(35)
Paraboloidul eliptic (35) poate fi generat de parabola G care se sprijina pe parabola din planul xOy (parabola COD) cand planul yOz se deplaseaza paralel cu el insusi.
Paraboloidul hiperbolic (fig 6) dat prin ecuatia redusa (12), sectionat cu planul y=k determina parabola:
G
: y=k, ![]() (35)
(35)
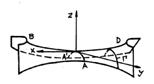
Fig 6
Sectionat cu planul z=h
determina conica: z=h, ![]() , care este hiperbola pentru h 0
si pereche de drepte concurente pentru h=0.
, care este hiperbola pentru h 0
si pereche de drepte concurente pentru h=0.
Prin sectionarea acestei cuadrice cu oricare alt plan, conica obtinuta este parabola, hiperbola sau pereche de drepte concurente.
Paraboloidul hiperbolic de ecuatie redusa (12) poate fi generat de parabola G care se sprijina pe parabola BOD cand planul xOz se misca paralel cu el insusi.
Conul patratic (fig 7) dat prin ecuatia redusa (14), sectionat cu planul z=k determina conica:
z=k, ![]() (37)
(37)
care este elipsa pentru k 0 si punct dublu pentru k=0. Sectionat cu planul x=h se obtine conica:
![]() (38)
(38)
care este hipebola pentru h 0
si pereche de drepte concurente pentru h=0. Sectionat cu planul ![]() se obtine conica:
se obtine conica:
![]() (39)
(39)
care este parabola pentru t 0
si dreapta dubla pentru t=0.
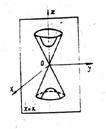
Fig 7
Sectionand un con patratic cu un plan oarecare se poate arata ca se obtine fie o conica propriu-zisa (elipsa, hiperbola sau parabola), fie una din conicile degenerate (punct dublu, pereche de drepte concurente sau dreapta dubla).
Cilindrul eliptic (fig 8) dat prin ecuatia redusa (16), intersectat cu planul z=k, determina elipsa:
z=k, ![]() (40)
(40)
intersectat cu planul y=h da conica:
y=h, ![]() (41)
(41)
care este o conica degenerata intr-o pereche de drepte strict paralele pentru h2<b2, dreapta dubla pentru h2=c2 si pereche vida de drepte paralele pentru h2>b2.
Sectionat cu un plan oarecare cilindrul eliptic nu poate determina altceva decat: elipsa, pereche de drepte strict paralele, pereche vida de drepte
paralele sau dreapta dubla.
Rezultate similare se pot stabili pentru cilindrul hiperbolic (fig.9) respectiv cilindrul parabolic (10).
Celelalte cuadrice degenerate prin sectiune determina doar conice degenerate.
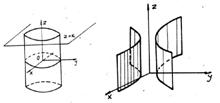
Fig.8 Fig
9
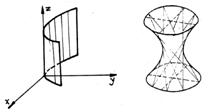
Fig.10 Fig 11
Observatie. Sectiunea cu un plan a unui con patratic determina o elipsa, o hiperbola sau parabola, conul patratic fiind singura cuadrica din care se poate obtine prin sectiune cu un plan oricare din conicile propriu-zise. Din acest motiv conicele propriu-zise se mai numesc si sectiuni conice.
Generatoare rectilinii ale unor cuadrice
Suprafetele generate prin deplasarea unei drepte se numesc suprafete riglate. Desigur, cuadricele degenerate (con, cilindru, perechea de plane ) sunt suprafete riglate. Vom arata ca hiperboloidul cu o panza si parabolic sunt de asemenea suprafete riglate.
Hiperboloidul cu o panza
Scriem ecuatia hiperboloidului cu o
panza, ![]() sub forma:
sub forma:
![]()
Ecuatiile:
a)
![]()
b) ![]() (
(![]() ) (42)
) (42)
determina o familie de drepte. Fie Dl o dreapta arbitrara din aceasta familie de drepte obtinuta pentru o valoare oarecare data parametrului l
Fie de asemenea un punct oarecare M(x,y,z)ID
Coordonatele
acestui punct verifica ecuatiile (10-42) deci si ecuatia hiperboloidului (care
se obtine prin inmultirea celor doua ecuatii (42). Deci, pentru orice ![]() , dreapta Dl
este situata pe suprafata. Familia de drepte (42) se numeste familia de
generatoare rectilinii l
a hiperboloidului. Analog se arata ca familia de drepte:
, dreapta Dl
este situata pe suprafata. Familia de drepte (42) se numeste familia de
generatoare rectilinii l
a hiperboloidului. Analog se arata ca familia de drepte:
![]() ,
,
![]() (43)
(43)
constituie de asemenea o familie de generatoare rectilinii (m) (fig.11).
Propietati ale generatoarelor rectilinii:
1. Prin fiecare punct al suprafetei trece cate o generatoare din fiecare
familie si numai una.
Fie M0(x0,y0,z0) un punct al suprafetei. Alegem valoarea lui l astfel incat ecuatia (42) sa fie verificata de punctul (x0,y0,z0). Aceasta valoare a lui l este unic determinata intrucat ecuatia (42) este de gradul intai in l. Intrucat coordonatele (x0,y0,z0) satisfac si ecuatia hiperboloidului si ecuatia
(42) rezulta ca ele satisfac si ecuatia (42).
2. Doua generatoare din aceeasi familie nu se intersecteaza: in caz contrar, prin punctul comun ar trece doua generatoare din aceeasi familie.
3. Oricare doua generatoare din familii diferite, Dl si Dm, se intersecteaza intr-un punct al suprafetei.
Aratam ca pentru orice l 0 si m 0, ecuatiile (42) si (43) au o solutie comuna. Rezolvand sistemul format de (42), (42) si (43) obtinem:
![]() (44)
(44)
si, printr-un calcul simplu, rezulta ca aceste valori satisfac si ecuatia (43). Ecuatiile (44) constituie deci o reprezentare parametrica a hiperboloidului cu o panza.
4. Generatoarele care trec printr-un punct M determina planul tangent la suprafata in acel punct.
Aceasta proprietate este valabila pentru orice suprafata riglata adica pentru orice suprafata riglata planul tangent intr-un punct M al acesteia contine generatoarea care trece prin M; intr-adevar tangenta in M la generatoare este insasi generatoarea, deci aceasta este continuta in planul tangent.
5. Generatoarele l si m sunt singurele drepte situate pe suprafata. Intr-adevar, presupunand ca ar exista o alta dreapta D pe suprafata daca M0ID rezulta ca prin M0 trec trei generatoare (doua din familiile (l) si (m), si dreapta D). Aceste trei drepte s-ar afla deci in planul tangent la hiperboloid in M0; astfel exprimat, planul tangent intr-un punct ar intersecta suprafata de gradul doi dupa trei drepte. Ori pentru orice cuadrica, planul tangent intr-un punct taie cuadrica dupa doua drepte ce trec prin punctul de contact. intr-adevar, luand originea in punctul de contact si planul tangent ca plan xoy, ecuatia cuadricei este: f(x,y,z)+2a30z=0 (f fiind forma patratica asociata formei patratice afine f(x,y,z)). Planul tangent are ecuatia z=0. Deci curba de intersectia are ecuatiile:
z=0, a11x2+2a12xy+a22y2=0,
deci este formata din doua drepte (reale sau imaginare, eventual confundate) care trec origine.
Paraboloidul hiperbolic.
Ecuatia paraboloidului hiperbolic:
![]()
poate fi scrisa sub forma :
![]() (46)
(46)
Din (27) obtinem doua familii de generatoare rectilinii (l) si (m
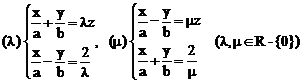 (47)
(47)
Se poate demonstra ca cele cinci proprietati ale generatoarelor rectilinii ale hiperboloidului cu o panza sunt valabile si pentru paraboloidul hiperbolic.
Ecuatiile parametrice ale acestuia sunt:
![]() (48)
(48)
Clasificarea cuadricelor dupa invariantii geometrici ai lor
Dupa cum rezulta din cele aratate in capitolul anterior, invariantii afini ai
unei forme patratice afine f sunt:
r=rang
A, r'=rang D, signd,
signD,
![]()
si p, indicele pozitiv de inertie al formei patratice corespunzatoare formei patratice afine date.
Invariantii geometrici ai cuadricei S : f(x,y,z)=0 sunt acei invarianti afini ai lui f care nu depind de inmultirea formelor patratice afine cu un numar. La inmultirea formei patratice afine f cu un numar r 0, notand f'=r f avem: A'=rA, D'=rD
iar in ipoteza ![]() Rezulta de aici ca
r=rang A, r'=rang D sunt intotdeauna invarianti geometrici ai cuadricei S.
Daca D 0
atunci si
Rezulta de aici ca
r=rang A, r'=rang D sunt intotdeauna invarianti geometrici ai cuadricei S.
Daca D 0
atunci si
signD este un invariant geometric.
Observatie.
Daca
notam cu p, numarul patratelor pozitive din ecuatia redusa a unei cuadrice
constatam ca in cazurile r'=r (cuadrice din grupa a) si r'=r+2 (cuadrice din
grupa c)) avem ![]() . Pentru cuadricele cu r'=r+1, convenind ca termenul liber
din ecuatia redusa sa fie -1, rezulta ca p poate fi 0,1,2 sau 3.
. Pentru cuadricele cu r'=r+1, convenind ca termenul liber
din ecuatia redusa sa fie -1, rezulta ca p poate fi 0,1,2 sau 3.
Cuadricele cu D 0 deci r'=4 se numesc cuadrice propiu-zise iar cuadricele cu D=0, deci r'<4 se numesc cuadrice singulare sau degenerate.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4963
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved