| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Fisa de lucru individuala (recapitulativa)
SEGMENTE PROPORTIONALE.
TEOREMA LUI THALES
CLASA a VII-a
Raportul a doua segmente
Se dau doua segmente [ AB] =6 cm. si [CD] = 8 cm.Raportul segmentelor [AB] si [
CD] ![]() este
este ![]() =
=![]() =
=![]() . Lungimile segmentelor trebuie exprimate
prin aceleasi unitati de masura.
. Lungimile segmentelor trebuie exprimate
prin aceleasi unitati de masura.
Segmente proportionale
Sirurile de numere ![]() si (
si ( ![]() daca
daca 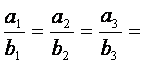 ....=k Raportul constant k se numeste factor de
proportionalitate.
....=k Raportul constant k se numeste factor de
proportionalitate.
Sirurile de segmente ( [AB] , [CD] , [EF] ..)si ( [![]() ] , [
] , [![]() ] ,[
] ,[![]() ] ...) se numesc proportionale daca sirurile lungimilor lor
sunt proportionale.
] ...) se numesc proportionale daca sirurile lungimilor lor
sunt proportionale.
Exemplu
AB=2dm, CD=12 dm , EF =3dm ,
FG = 9 dm , GH = 18 dm, BC=6 dm atunci
([AB], [BC ], [ CD ])~ ([EF], [FG] , [Gh ] ) deoarece 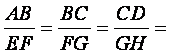
![]()
![]()
Factorul de proportionalitate este ![]()
Impartirea unui segment intr-un raport dat
Exista un singur punct interior segmentului care imparte un segment intr-un raport dat.
Fie [AB] segmental dat si r
raportul dat. Trebuie sa gasim un punct M ,M![]() (AB) astfel incat
(AB) astfel incat ![]() r, ceea ce inseamna
r, ceea ce inseamna ![]() De aici rezulta ca
AM=AB
De aici rezulta ca
AM=AB![]()
![]()
![]()
![]() . Deoarece
. Deoarece
![]() rezulta ca AM <AB , deci punctul
M este in interiorul segmentului AB
rezulta ca AM <AB , deci punctul
M este in interiorul segmentului AB
Daca r=1 atunci M este mijlocul segmentului .
Teoreme paralelelor echidistante
Daca mai multe drepte paralele determina pe o secanta segmente congruente , atunci ele determina pe orice alta secanta segmente congruente
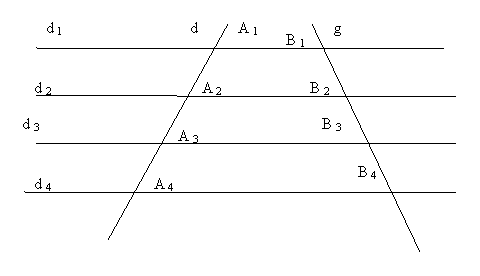
[A![]() A
A![]() ] A
] A![]() A
A![]() ] =[A
] =[A![]() A
A![]() ] Comform teoremei
rezulta si ca
] Comform teoremei
rezulta si ca
[B![]() B
B![]() ] B
] B![]() B
B![]() ] =[ B
] =[ B![]() B
B![]() ]
]
Aplicatie
Pentru a imparti un segment in mai multe parti egale se aplica teorema paralelelor echidistante.
5.Teorema paralelelor neechidistante
Mai multe drepte paralele determina pe doua secante oarecare segmente proportionale.
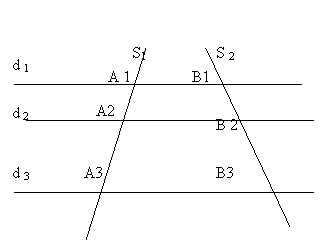
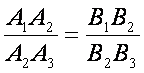
Teorema lui Thales
O paralela dusa la una din laturile unui triunghi imparte celelalte doua laturi in segmente proportionale.
Reciproc Daca o dreapta determina pe doua laturi ale unui triunghi segmente proportionale , atunci ea este paralela cu a treia latura
.
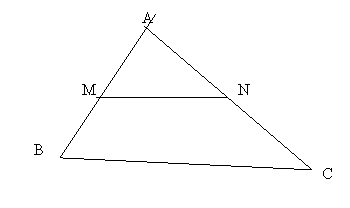 M N ║ BC
M N ║ BC ![]()
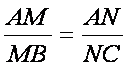
Probleme.
Se da triunghiul ABC , M![]() . (CB, N
. (CB, N![]() (CA si MN ║ AB. Sa se completeze tabloul de mai jos :
(CA si MN ║ AB. Sa se completeze tabloul de mai jos :
|
BC |
AC |
CM |
CN |
MB |
NA |
|
8 |
6 |
4 |
| ||
|
9 |
6 |
2 | |||
|
12 |
4 |
9 |
|||
|
30 |
35 |
12 | |||
|
1,7 |
2,6 |
1,4 |
|||
|
3 |
8 |
7 |

2.Teorema bisectoarei
Intr-un triunghi bisectoarea unui unghi determina pe latura opusa segmente proportionale cu celelalte doua laturi
Demonstratie:
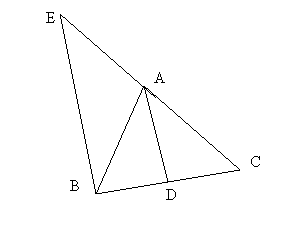
![]() Fie triunghiul ABC ;AD
bisectoarea unghiului BAC; trebuie sa demonstram ca
Fie triunghiul ABC ;AD
bisectoarea unghiului BAC; trebuie sa demonstram ca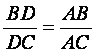 Ducem prin B paralela la bisectoarea AD, care intersecteaza
prelungirea lui AC in E. Triunghiul ABE are unghiurile B si E congruente
Ducem prin B paralela la bisectoarea AD, care intersecteaza
prelungirea lui AC in E. Triunghiul ABE are unghiurile B si E congruente
![]()
![]() EBA ca alterne interne;
EBA ca alterne interne; ![]() ca unghiuri
corespondente
ca unghiuri
corespondente ![]() )
)
Aplicand teorema lui Thales, obtinem :
![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4225
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved