| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Siruri de variabile aleatoare. Legea numerilor mari.
Teoreme limita.
Teorema 5.1. (Inegalitatea lui Cebisev). Daca
variabila aleatoare X are valoare medie si dispersie, atunci
pentru orice ![]() are loc inegalitatea
are loc inegalitatea
![]()
care este echivalenta cu
![]()
Demonstratie. Vom considera cazul cand variabila aleatoare X este de tip continuu,
adica are densitatea de probabilitate ![]() . In cazul discret, demonstratia urmeaza
aceeasi cale.
. In cazul discret, demonstratia urmeaza
aceeasi cale.
De asemenea, ne ocupam numai de a doua forma a inegalitatii.
Din proprietatile densitatii de probabilitate avem ca
![]()
Deoarece ![]() avem ca
avem ca ![]() prin urmare, putem
face urmatoarele majorari:
prin urmare, putem
face urmatoarele majorari:
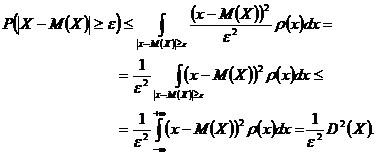
Retinand extremitatile acestuii sir de relatii avem ca
![]()
adica a doua forma a inegalitatii lui Cebisev.
Din aceasta forma a inegalitatii se obtine cealalta, daca se foloseste probablitatea evenimentului contrar, adica
![]()
Observatia 5.2. Daca in inegalitatea lui Cebisev se
ia ![]() unde
unde![]() atunci aceasta devine
atunci aceasta devine
![]()
Astfel, pentru ![]() se obtine
se obtine
![]()
ceea ce inseamna ca probabilitatea ca valorile lui X sa se abata de la valoarea medie
![]() mai putin de trei
ori abaterea standard este nai mare decat
mai putin de trei
ori abaterea standard este nai mare decat ![]()
Definitia 5.3. Spunem ca sirul de variabile
aleatoare ![]() converge in
probabilitate la variabila aleatoare X,
si vom nota
converge in
probabilitate la variabila aleatoare X,
si vom nota ![]() daca pentru orice
daca pentru orice
![]() avem ca
avem ca
![]()
Definitia 5.4. Spunem ca sirul de variabile
aleatoare ![]() converge in medie de
ordin k la variabila aleatoare X, si vom nota
converge in medie de
ordin k la variabila aleatoare X, si vom nota ![]() daca
daca
![]()
Observatia 5.5. In cazul particular ![]() avem ceea ce numim
convergenta in medie patratica. Asadar, aceasta are loc
daca
avem ceea ce numim
convergenta in medie patratica. Asadar, aceasta are loc
daca
![]()
Definitia 5.6. Spunem ca sirul de variabile
aleatoare ![]() converge in
repartitie la variabila aleatoare X,
si vom nota
converge in
repartitie la variabila aleatoare X,
si vom nota ![]() daca avem ca
daca avem ca
![]() unde
unde ![]() si F sunt respectiv functiile de
repartitie ale variabilelor aleatoare
si F sunt respectiv functiile de
repartitie ale variabilelor aleatoare ![]() si X, iar limita considerata
exista pentru orice punct de continuitate
si X, iar limita considerata
exista pentru orice punct de continuitate ![]() al functiei F.
al functiei F.
Observatia 5.7. Se arata ca daca ![]() atunci
atunci ![]() care la randul sau implica
care la randul sau implica ![]()
De asemenea, avem ca daca ![]() pentru
pentru ![]() , atunci
, atunci ![]()
Definitia 5.8. Spunem ca sirul de varibile
aleatoare ![]() urmeaza legea
(slaba) a numerelor mari, daca pentru orice
urmeaza legea
(slaba) a numerelor mari, daca pentru orice ![]() avem ca
avem ca
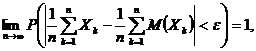
adica
![]()
Teorema 5.9. (Markov). Daca sirul de variabile
aleatoare ![]() verifica
conditia (lui Markov)
verifica
conditia (lui Markov)
![]()
atunci aceasta urmeaza legea numerelor mari, adica
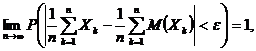
oricare ar fi ![]()
Demonstratie. Se utilizeaza inegalitatea lui Cebisev pentru variabila aleatoare
![]() anume
anume
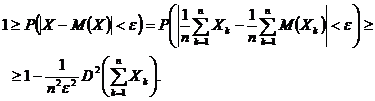
Trecand la imita in dubla inegalitate, astfel obtinuta, si avand in vedere conditia lui Markov, rezulta ca
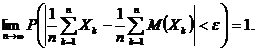
Teorema 5.10. (Cebisev). Fie sirul ![]() de variabile aleatoare
independente doua cate doua
si care au dispersiile egal marginite, adica
de variabile aleatoare
independente doua cate doua
si care au dispersiile egal marginite, adica ![]() (L finit), atunci
sirul urmeaza legea numerelor mari, adica
(L finit), atunci
sirul urmeaza legea numerelor mari, adica
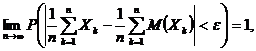
oricare ar fi ![]()
Demonstratie. Deoarece variabilele aleatoare sunt independente doua cate doua si au dispersiile egal marginite, se obtine ca
![]()
Daca se retin extremitatile acestui sir de relatii si se trece la limita, rezulta ca
![]()
deci conditia lui Markov este indeplinita. Aplicind teorema lui Markov se obtine afirmatia din teorema lui Cebisev.
Observatia 5.11. Daca in teorema lui
Cebisev, variabilele aleatoare au aceeasi valoare medie, adica ![]() atunci avem
atunci avem
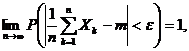
adica ![]() Prin urmare, media
aritmetica a primelor n
variabile aleatoare din sirul considerat isi pierde caracterul
aleator, pentru
Prin urmare, media
aritmetica a primelor n
variabile aleatoare din sirul considerat isi pierde caracterul
aleator, pentru ![]() .
.
Teorema 5.12. (Poisson). Daca intr-un sir de
repetari independente ale unui experiment, probabilitatea de
aparitie a evenimentului fixat A, la repetarea de rang n, este ![]() atunci
atunci
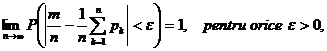
m fiind numarul aparitiilor evenimentului A in primele n repetari ale experimentului.
Demonstratie. Fie ![]() variabila aleatoare
care ne indica aparitia evenimentului A la repetarea de rang k
a experimentului. Atunci, variabila aleatoare
variabila aleatoare
care ne indica aparitia evenimentului A la repetarea de rang k
a experimentului. Atunci, variabila aleatoare ![]() va avea
distributia
va avea
distributia
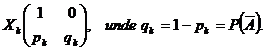
Variabilele aleatoare, astfel introduse, sunt
independente si au dispersiile egal marginite, anume ![]() Folosind teorema lui
Cebisev si avand in vedere ca
Folosind teorema lui
Cebisev si avand in vedere ca
![]() obtinem rezultatul din enuntul teoremei.
obtinem rezultatul din enuntul teoremei.
Teorema 5.13. (Bernoulli). Daca intr-un sir de repetari independente ale unui experiment, probabilitatea de aparitie a evenimentului fixat A, la fiecare repetare este
![]() atunci
atunci
![]()
unde m este numarul aparitiilor evenimentului A in primele n repetari ale experimentului.
Demonstratie. Conditiile sunt aceleasi cu cele din teorema lui Poisson cu
![]() . Prin urmare, folosind teorema lui Poisson, se obtine
rezultatul dorit.
. Prin urmare, folosind teorema lui Poisson, se obtine
rezultatul dorit.
Teorema 5.14. (Leapunov). Fie sirul ![]() de variabile aleatoare
independente pentru care exista momentele centrate de ordinul trei si
care satisfac conditia (Leapunov)
de variabile aleatoare
independente pentru care exista momentele centrate de ordinul trei si
care satisfac conditia (Leapunov)
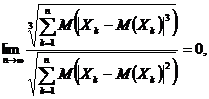
si fie
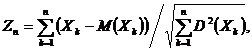
atunci sirul de variabile aleatoare ![]() converge in
repartitie la o variabila aleatoare ce urmeaza legea
normala
converge in
repartitie la o variabila aleatoare ce urmeaza legea
normala ![]() , adica
, adica
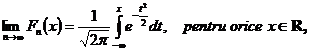
![]() fiind functia de
repartitie a variabilei aleatoare
fiind functia de
repartitie a variabilei aleatoare ![]() .
.
Observatia 5.15. Problema determinǎrii legii de probabilitate a variabilei
aleatoare ![]() , definitǎ mai sus, cand
, definitǎ mai sus, cand ![]() , poartǎ denumirea de problemǎ limitǎ, iar
teorema care rezolvǎ o problemǎ limitǎ se numeste teoremǎ limitǎ.
, poartǎ denumirea de problemǎ limitǎ, iar
teorema care rezolvǎ o problemǎ limitǎ se numeste teoremǎ limitǎ.
Dacǎ legea de probabilitate limitǎ este normalǎ, atunci avem o teoremǎ limitǎ centralǎ.
Prin urmare, teorema lui Leapunov este o teoremǎ limitǎ centralǎ si aratǎ rolul important pe care il are legea normalǎ, ceea ce se va vedea si mai departe, in statistica matematic
Corolarul 5.16. Fie
sirul de variabile aleatoare independente si identic repartizate ![]() adicǎ au aceeasi lege de probabilitate, si fie
adicǎ au aceeasi lege de probabilitate, si fie ![]() si
si ![]() pentru orice
pentru orice ![]() , atunci sirul variabilelor aleatoare
, atunci sirul variabilelor aleatoare ![]() unde
unde
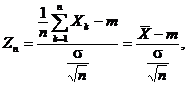
converge in repartitie
la o variabilǎ aleatoare ce urmeazǎ legea normalǎ ![]() adicǎ
adicǎ
![]()
![]()
![]() fiind functia de
repartitie a variabilei aleatoare
fiind functia de
repartitie a variabilei aleatoare ![]() .
.
Demonstratie. Vericǎm dacǎ este indeplinitǎ conditia din teorema lui Leapunov. Pentru aceasta avem c
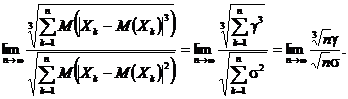
Fiind indeplinitǎ conditia lui Leapunov, avem cǎ
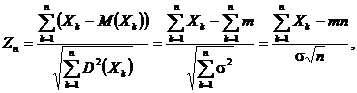
adicǎ
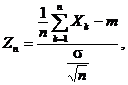
urmeazǎ legea normalǎ ![]() , cand
, cand ![]() , ceea ce trebuie arǎtat.
, ceea ce trebuie arǎtat.
Teorema 5.17. (Moivre-Laplace). Dacǎ variabila aleatoare X urmeazǎ legea binomialǎ, adicǎ are distributia
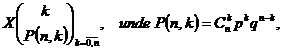
atunci, pentru ![]() avem c
avem c
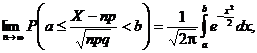
adicǎ
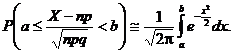
Demonstratie. Dacǎ se considerǎ variabiale
aleatoare ![]() independente, cu aceeasi distributie
independente, cu aceeasi distributie ![]()
atunci ![]()
Pe de altǎ
parte, avem cǎ ![]() si folosind
rezultatul corolarului precedent, se obtine cǎ
si folosind
rezultatul corolarului precedent, se obtine cǎ
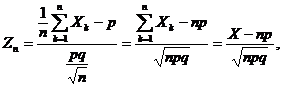
urmeazǎ legea normalǎ ![]() pentru
pentru ![]() . Prin urmare, se obtine cǎ
. Prin urmare, se obtine cǎ
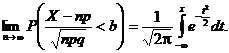
Folosind acest rezultat, se poate scrie succesiv
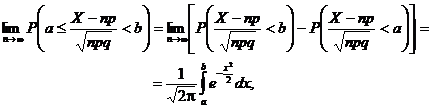
Observatia
5.18. Deoarece ![]() se
obisnuieste ca formulele din teorema lui Moivre-Laplace sǎ se scrie
se
obisnuieste ca formulele din teorema lui Moivre-Laplace sǎ se scrie
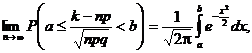
respectiv
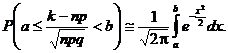
Observatia 5.19. Folosind functia lui Laplace,
![]()
tabelatǎ in Anexa I, avem cǎ
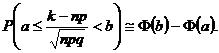
Observatia 5.20. Deoarece functia lui Laplace este
functie imparǎ, adicǎ ![]() aceasta trebuie
tabelatǎ numai pentru argumente pozitive. Asadar, vom avea
aceasta trebuie
tabelatǎ numai pentru argumente pozitive. Asadar, vom avea
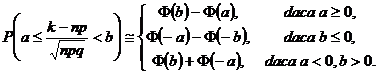
Aplicatia 5.21. Dacǎ se doreste calculul
urmǎtoarei probabilitǎti ![]() aceasta se obtine
din faptul cǎ
aceasta se obtine
din faptul cǎ
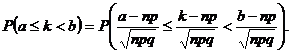
Astfel, rezultǎ cǎ
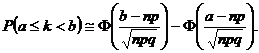
Exemplul 5.22. Probabilitatea ca o unitate hoteliera
sa fie ocupata in mod acceptabil intr-o zi este ![]() . Vrem sa calculam probabilitatea ca unitatea
respectiva sa fie ocupata acceptabil intr-o luna de 30 de
zile, un numar de zile cuprins intre 10 si 25.
. Vrem sa calculam probabilitatea ca unitatea
respectiva sa fie ocupata acceptabil intr-o luna de 30 de
zile, un numar de zile cuprins intre 10 si 25.
Daca
notam prin k numarul de
zile cand unitatea este ocupata acceptabil, avem de calculat
probabilitatea 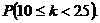 Deoarece
Deoarece ![]() si
si
![]() avem ca
avem ca
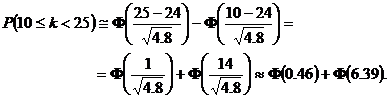
Din Anexa I se extrag valorile ![]() si
si ![]() deci putem scrie
ca
deci putem scrie
ca
![]() .
.
Observatia 5.23. (Regula celor trei ![]() ). Daca in formula Moivre-Laplace se
considera
). Daca in formula Moivre-Laplace se
considera ![]() atunci
atunci
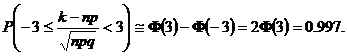
Prin urmare, rezulta ca ![]() . Deoarece, abaterea medie patratica a variabilei
aleatoare X ce urmeaza legea
binomiala este
. Deoarece, abaterea medie patratica a variabilei
aleatoare X ce urmeaza legea
binomiala este ![]() avem regula
urmatoare cunoscuta sub denumirea de regula celor trei
avem regula
urmatoare cunoscuta sub denumirea de regula celor trei ![]() : probabilitatea ca frecventa absoluta k sa se abata de la valoarea
medie
: probabilitatea ca frecventa absoluta k sa se abata de la valoarea
medie ![]() mai putin de trei
ori abaterea medie patratica este mai mare decat
mai putin de trei
ori abaterea medie patratica este mai mare decat ![]() .
.
Aplicatia 5.24. Daca variabila aleatoare X urmeaza legea hipergeometrica, adica are distributia
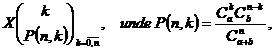
atunci pentru ![]() si n suficint de mari se obtine
si n suficint de mari se obtine
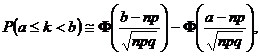
unde ![]()
![]() . Acest rezultat se bazeaza pe Observatia 3.12.
. Acest rezultat se bazeaza pe Observatia 3.12.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3124
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved