| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
INTEGRAREA NUMERICA A FUNTIILOR
INTEGRAREA NUMERICA A FUNCTIILOR
1. INTRODUCERE
Fie ![]() o functie
definita si integrabila pe intervalul
o functie
definita si integrabila pe intervalul ![]() . De cele mai multe ori este greu de determinat o primitiva,
F, a integralei definite
. De cele mai multe ori este greu de determinat o primitiva,
F, a integralei definite
![]() (3.1)
(3.1)
sau daca aceasta primitiva exista, dar are o expresie analitica foarte complicata, folosirea in calculele ulterioare este foarte greoaie. De aceea, pentru calculul integralei (3.1) se stabilesc formule aproximative simple si usor de folosit pe orice calculator.
Formula:
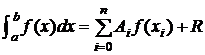 , (3.2)
, (3.2)
in care ![]() sunt constante independente de f, iar
sunt constante independente de f, iar ![]() sunt nodurile
intervalului
sunt nodurile
intervalului ![]() , poarta numele de formula de cuadratura numerica.
, poarta numele de formula de cuadratura numerica.
In continuare, se deduc expresiile catorva formule de integrare numerica si se intocmesc procedurile de calcul, scrise in limbaj Turbo-Pascal.
3.2. Metoda coeficientilor nedeterminati
Metoda coeficientilor
nedeterminati consta in determinarea coeficientilor ![]() , ai formulei de cuadratura numerica (3.2), astfel
incat restul R sa fie nul pentru
orice polinom de grad mai mic sau egal cu n.
, ai formulei de cuadratura numerica (3.2), astfel
incat restul R sa fie nul pentru
orice polinom de grad mai mic sau egal cu n.
Pentru demonstratie, se
aleg polinoamele particulare: 1, x, ![]() . Daca in formula de cuadratura (3.2) se
inlocuieste, pe rand, functia
. Daca in formula de cuadratura (3.2) se
inlocuieste, pe rand, functia ![]() cu polinoamele
mentionate si se pune conditia ca restul R sa fie nul, rezulta:
cu polinoamele
mentionate si se pune conditia ca restul R sa fie nul, rezulta:
![]() ;
;
![]() ;
;
![]() ; (3.3)
; (3.3)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
![]() .
.
Relatiile (3.3)
formeaza un sistem de (n+1)
ecuatii liniare in necunoscutele ![]() , si anume:
, si anume:
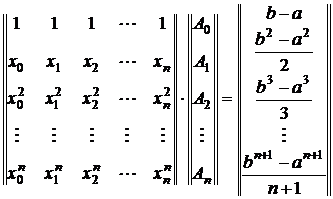 (3.4)
(3.4)
Deoarece nodurile
intervalului ![]() se considera
distincte, determinantul sistemului (3.4) este diferit de zero (determinant de
tip Vandermonde), iar solutia sistemului este unica. Se poate
arata ca restul formulei de cuadratura este nul pentru orice
polinom de grad mai mic sau egal cu n,
nu numai pentru polinoamele particulare considerate [36].
se considera
distincte, determinantul sistemului (3.4) este diferit de zero (determinant de
tip Vandermonde), iar solutia sistemului este unica. Se poate
arata ca restul formulei de cuadratura este nul pentru orice
polinom de grad mai mic sau egal cu n,
nu numai pentru polinoamele particulare considerate [36].
3.3. Formula trapezelor de cuadratura numerica
Fie functia ![]() , continua pe
, continua pe ![]() , unde a < b. Se cere sa se calculeze
, unde a < b. Se cere sa se calculeze
![]() .
.
Fie ![]() , o retea de noduri echidistante pe intervalul
, o retea de noduri echidistante pe intervalul ![]() . Ca urmare a proprietatii de aditivitate a
integralei fata de interval, se poate scrie:
. Ca urmare a proprietatii de aditivitate a
integralei fata de interval, se poate scrie:
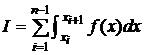 . (3.7)
. (3.7)
Pentru determinarea formulei
trapezelor de cuadratura numerica, se aproximeaza functia ![]() , pe fiecare interval, cu un polinom Newton de interpolare
dreapta de ordinul unu. In acest caz, relatia (3.7) devine:
, pe fiecare interval, cu un polinom Newton de interpolare
dreapta de ordinul unu. In acest caz, relatia (3.7) devine:
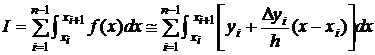 , (3.8)
, (3.8)
unde: ![]() ,
, ![]() este pasul
retelei, iar
este pasul
retelei, iar ![]() este diferenta finita progresiva de ordinul
unu.
este diferenta finita progresiva de ordinul
unu.
Daca in relatia (3.8)
se face schimbarea de variabila ![]() , rezulta:
, rezulta:
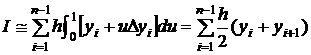 . (3.9)
. (3.9)
In cazul in care functia
![]() este data
tabelar, adica se cunosc valorile
este data
tabelar, adica se cunosc valorile ![]() in nodurile
retelei, relatia (3.9) devine:
in nodurile
retelei, relatia (3.9) devine:
![]() . (3.10)
. (3.10)
Daca se cunoaste
expresia analitica a functiei ![]() si se cere
calculul integralei I , pe intervalul
si se cere
calculul integralei I , pe intervalul
![]() , atunci relatia (3.9) capata forma:
, atunci relatia (3.9) capata forma:
![]() (3.11)
(3.11)
Metoda trapezelor, de calcul
al integralei definite pe intervalul ![]() , consta in inlocuirea curbei
, consta in inlocuirea curbei ![]() cu o linie
poligonala, dupa cum se vede in figura 3.1.
cu o linie
poligonala, dupa cum se vede in figura 3.1.
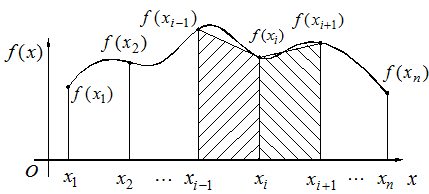
Fig. 3.1. Reprezentarea geometrica a metodei trapezelor
Eroarea de trunchiere pe
intervalul ![]() , in cazul formulei de cuadratura numerica a
trapezelor, este de forma:
, in cazul formulei de cuadratura numerica a
trapezelor, este de forma:
![]() . (3.12)
. (3.12)
Fie ![]() o primitiva a
functiei
o primitiva a
functiei ![]() . Conform formulei lui Leibniz-Newton, relatia (3.12)
devine:
. Conform formulei lui Leibniz-Newton, relatia (3.12)
devine:
![]() . (3.13)
. (3.13)
Daca se dezvolta in
serie Taylor functiile ![]() si
si ![]() , in jurul punctului
, in jurul punctului ![]() , se obtine:
, se obtine:
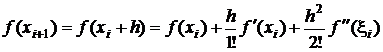 ;
;
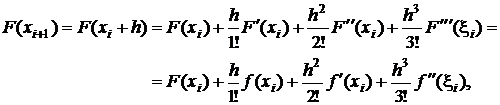 (3.14)
(3.14)
unde ![]() ,
, ![]() .
.
Dupa inlocuiri in relatia (3.13), se obtine:
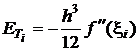 . (3.15)
. (3.15)
Daca se considera
intervalul ![]() , atunci eroarea de trunchiere, in cazul metodei trapezelor,
este
, atunci eroarea de trunchiere, in cazul metodei trapezelor,
este
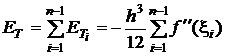 . (3.16)
. (3.16)
Pentru ![]() , astfel incat
, astfel incat 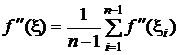 si tinand seama
de faptul ca nodurile sunt echidistante, adica
si tinand seama
de faptul ca nodurile sunt echidistante, adica ![]() , relatia (3.16)
devine:
, relatia (3.16)
devine:
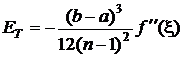 . (3.17)
. (3.17)
Daca exista ![]() , astfel incat
, astfel incat ![]() ,
, ![]()
![]() , atunci
, atunci
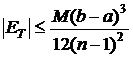 . (3.18)
. (3.18)
3.4. Formule Simpson de cuadratura numerica
3.4.1. Formula Simpson 1/3
Fie functia ![]() , continua pe
, continua pe ![]() , unde a < b. Se cere sa se calculeze
, unde a < b. Se cere sa se calculeze
![]() .
.
Fie ![]() , o retea de noduri echidistante pe intervalul
, o retea de noduri echidistante pe intervalul ![]() . Ca urmare a proprietatii de aditivitate a
integralei fata de interval, se poate scrie
. Ca urmare a proprietatii de aditivitate a
integralei fata de interval, se poate scrie
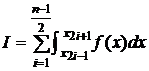 . (3.20)
. (3.20)
Pentru determinarea formulei
Simpson 1/3 de cuadratura numerica, se aproximeaza functia ![]() , pe fiecare interval de forma
, pe fiecare interval de forma ![]() , cu un polinom Newton de interpolare dreapta de ordinul doi
si relatia (3.20) devine:
, cu un polinom Newton de interpolare dreapta de ordinul doi
si relatia (3.20) devine:
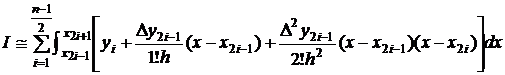 , (3.21)
, (3.21)
unde:
![]() ;
;
![]() este pasul
retelei de integrare;
este pasul
retelei de integrare;
![]() este diferenta
finita progresiva de ordinul unu;
este diferenta
finita progresiva de ordinul unu;
![]() este diferenta
finita progresiva de ordinul doi.
este diferenta
finita progresiva de ordinul doi.
Daca in relatia (3.21)
se face schimbarea de variabila ![]() , rezulta:
, rezulta:
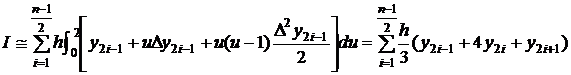 . (3.22)
. (3.22)
In cazul in care functia
![]() este data
tabelar, adica se cunosc valorile
este data
tabelar, adica se cunosc valorile ![]() in nodurile
retelei de integrare, relatia (3.22) devine:
in nodurile
retelei de integrare, relatia (3.22) devine:
![]() . (3.23)
. (3.23)
Daca se cunoaste
expresia analitica a functiei ![]() si se cere
calculul integralei I, pe intervalul
si se cere
calculul integralei I, pe intervalul ![]() , atunci relatia (3.22) devine:
, atunci relatia (3.22) devine:
![]() (3.24)
(3.24)
Metoda Simpson 1/3, de calcul
al integralei definite pe intervalul ![]() , consta in inlocuirea curbei
, consta in inlocuirea curbei ![]() , pe fiecare interval de forma
, pe fiecare interval de forma ![]() , cu un polinom de
gradul doi (v.fig.3.2). Numarul de puncte trebuie astfel ales incat
raportul
, cu un polinom de
gradul doi (v.fig.3.2). Numarul de puncte trebuie astfel ales incat
raportul ![]() sa fie numar
intreg. Daca nu se tine seama de acest lucru si mai ramane
un interval, suprafata corespunzatoare acestuia se calculeaza cu
metoda trapezelor.
sa fie numar
intreg. Daca nu se tine seama de acest lucru si mai ramane
un interval, suprafata corespunzatoare acestuia se calculeaza cu
metoda trapezelor.
Eroarea de trunchiere pe intervalul
![]() , in cazul formulei de cuadratura numerica (3.22),
este de forma:
, in cazul formulei de cuadratura numerica (3.22),
este de forma:
![]() . (3.25)
. (3.25)
Procedand in mod analog formulei trapezelor, se obtine:
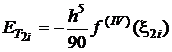 .
.
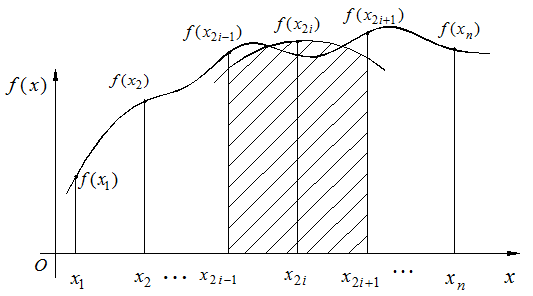
Fig. 3.2. Reprezentarea geometrica a metodei Simpson 1/3
Daca se considera
intervalul ![]() , atunci eroarea de trunchiere, in cazul metodei Simpson
1/3, este:
, atunci eroarea de trunchiere, in cazul metodei Simpson
1/3, este:
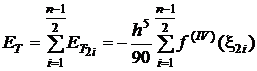 . (3.26)
. (3.26)
Pentru ![]() , astfel incat
, astfel incat 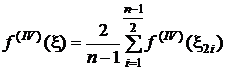 ,
,
relatia (3.26) devine:
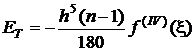 . (3.27)
. (3.27)
Pentru ![]() rezulta:
rezulta:
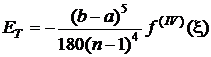 . (3.28)
. (3.28)
Daca exista ![]() , astfel incat
, astfel incat ![]() ,
, ![]()
![]() , atunci
, atunci
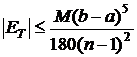 . (3.29)
. (3.29)
3.4.2. Formula Simpson 3/8
Fie functia ![]() , continua pe
, continua pe ![]() , unde a < b. Se cere sa se calculeze
, unde a < b. Se cere sa se calculeze
![]() .
.
Fie ![]() , o retea de noduri echidistante pe intervalul
, o retea de noduri echidistante pe intervalul ![]() . Ca urmare a proprietatii de aditivitate a
integralei fata de interval, se poate scrie
. Ca urmare a proprietatii de aditivitate a
integralei fata de interval, se poate scrie
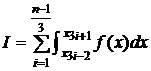 . (3.30)
. (3.30)
Pentru determinarea formulei
Simpson 3/8 de cuadratura numerica, se aproximeaza functia ![]() , pe fiecare interval de forma
, pe fiecare interval de forma ![]() , cu un polinom Newton de interpolare dreapta de ordinul trei
si relatia (3.30) devine:
, cu un polinom Newton de interpolare dreapta de ordinul trei
si relatia (3.30) devine:
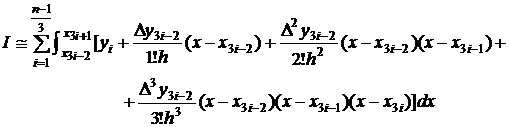 (3.31)
(3.31)
unde: ![]() ;
;
![]() este pasul
retelei de integrare;
este pasul
retelei de integrare;
![]() este diferenta
finita progresiva de ordinul unu;
este diferenta
finita progresiva de ordinul unu;
![]() este diferenta
finita progresiva de ordinul doi;
este diferenta
finita progresiva de ordinul doi;
![]() este diferenta
finita progresiva de ord. trei.
este diferenta
finita progresiva de ord. trei.
Daca in relatia (3.31)
se face schimbarea de variabila ![]() , rezulta:
, rezulta:
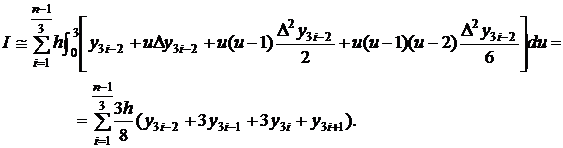 (3.32)
(3.32)
In cazul in care functia
![]() este data
tabelar, adica se cunosc valorile
este data
tabelar, adica se cunosc valorile ![]() , in nodurile retelei de integrare, atunci relatia
(3.32) devine:
, in nodurile retelei de integrare, atunci relatia
(3.32) devine:
![]() . (3.33)
. (3.33)
Daca se cunoaste
expresia analitica a functiei ![]() si se cere
calculul integralei I, pe intervalul
si se cere
calculul integralei I, pe intervalul ![]() , atunci relatia (3.32) devine:
, atunci relatia (3.32) devine:
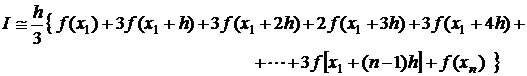
Metoda Simpson 3/8, de calcul
al integralei definite pe intervalul ![]() , consta in inlocuirea curbei
, consta in inlocuirea curbei ![]() pe fiecare interval de
forma
pe fiecare interval de
forma ![]() cu un polinom de
gradul trei. Numarul de puncte trebuie astfel ales incat raportul
cu un polinom de
gradul trei. Numarul de puncte trebuie astfel ales incat raportul ![]() sa fie numar
intreg (v.fig.3.3). Daca nu se tine seama de acest lucru si mai
ramane un interval, pentru acesta se aplica formula trapezelor;
daca raman doua intervale, atunci se aplica formula
corespunzatoare metodei Simpson 1/3.
sa fie numar
intreg (v.fig.3.3). Daca nu se tine seama de acest lucru si mai
ramane un interval, pentru acesta se aplica formula trapezelor;
daca raman doua intervale, atunci se aplica formula
corespunzatoare metodei Simpson 1/3.
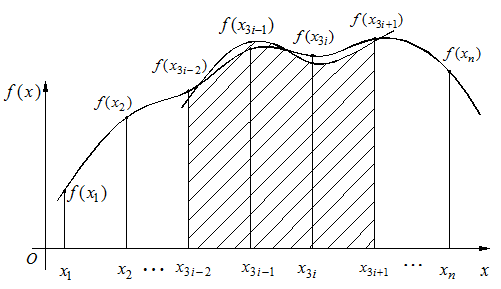
Fig. 3.3. Reprezentarea geometrica a metodei Simpson 3/8
Eroarea de trunchiere, pe
intervalul ![]() , in cazul formulei de cuadratura numerica (3.32),
este de forma:
, in cazul formulei de cuadratura numerica (3.32),
este de forma:
![]() . (3.35)
. (3.35)
sau
![]() . (3.36)
. (3.36)
Daca se dezvolta in
serie Taylor functiile ![]() si
si ![]() , in jurul punctului
, in jurul punctului ![]() , se obtine:
, se obtine:
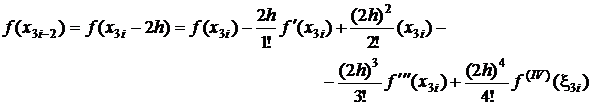 ;
;
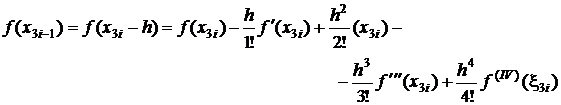 ;
;
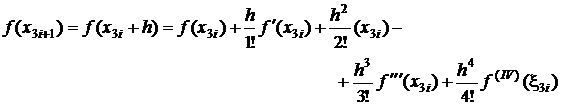 ;
;
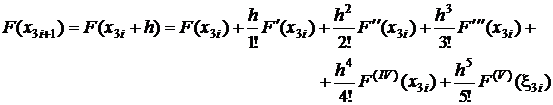 ;
;
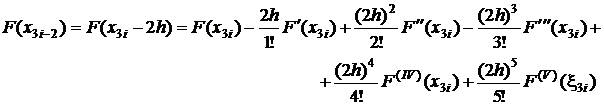
unde ![]() ,
, ![]() .
.
Dupa inlocuiri in relatia (3.36), se obtine:
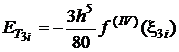 . (3.37)
. (3.37)
Daca se considera
intervalul ![]() , atunci eroarea de trunchiere in cazul metodei Simpson 3/8
este:
, atunci eroarea de trunchiere in cazul metodei Simpson 3/8
este:
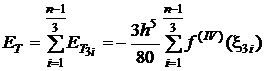 . (3.38)
. (3.38)
Pentru ![]() , astfel incat
, astfel incat 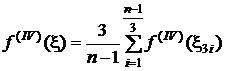 si tinand
seama de faptul ca nodurile sunt echidistante, adica
si tinand
seama de faptul ca nodurile sunt echidistante, adica ![]() , relatia (3.38) devine
, relatia (3.38) devine
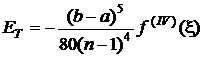 . (3.39)
. (3.39)
Daca exista ![]() , astfel incat
, astfel incat ![]() ,
, ![]()
![]() , atunci
, atunci
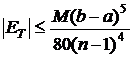 . (3.40)
. (3.40)
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2539
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved