| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Unitate de invatare: NUMERE COMPLEXE
Probleme propuse:
Sa se determine numerele complexe z, astfel incat:
a) ![]() b)
b) ![]()
2) Sa se determine numerele complexe z, astfel incat:
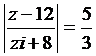 si
si 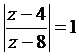
Sa se reprezinte in planul complex numerele:
a) ![]() b)
b) ![]()
4) Sa se determine numerele complexe z cu proprietatea ![]() .
.
Fie functia ![]() definita prin
definita prin ![]() . Sa se determine:
. Sa se determine:
a) multimea A a punctelor din planul complex care au ca afixe numerele complexe z cu Im f(z) = 0.
b) multimea B a punctelor din planul complex care au ca afixe numerele complexe z cu Re f(z) = 0.
Sa se rezolve in multimea numerelor complexe, ecuatiile:
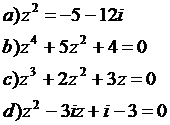
Daca α si ![]() sunt solutiile
ecuatiei z2 - z + 1 = 0, sa se calculeze
sunt solutiile
ecuatiei z2 - z + 1 = 0, sa se calculeze
![]() .
.
Aratati ca
numarul ![]() este real,
este real, ![]()
Daca z2
+ z + 1 =0, sa se afle ![]() .
.
10) Fie z1 , z2 є C
astfel incat ![]() . Sa se arate ca
. Sa se arate ca ![]() sau
sau ![]()
Fie a є R si 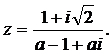 Determinati
valorile lui a pentru care z є R.
Determinati
valorile lui a pentru care z є R.
Fie a,b є R* ,
n є N si ![]() . Aratati ca daca
. Aratati ca daca ![]() , atunci
, atunci ![]()
Sa se rezolve in C ecuatiile:
a) ![]() b)
b) 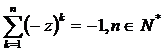 c)
c) 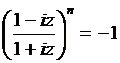
14) Sa se arate ca daca ![]() , atunci
, atunci ![]()
Fie z = cost + isint, iar n є N*, atunci:
a)Sa se demonstreze
formulele: ![]() si
si ![]()
b)Sa se calculeze ![]()
INDICATII SI RASPUNSURI
1) a) Rezolvam ecuatia ![]() , unde z = x+iy
, unde z = x+iy ![]()
![]()
![]() -2iy = -4i
-2iy = -4i ![]() y = 2 si
y = 2 si ![]()
Deci solutiile sunt z1 = 2i si z2 = ![]() +2i.
+2i.
b) Se rezolva in mod analog cu punctul a) si se obtine
solutia 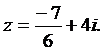
2)Fiez = x+iy, atunci ![]()
![]()
![]()
![]() x = 6 si analog utilizand ipoteza
x = 6 si analog utilizand ipoteza 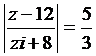 vom avea y1 = 17 si y2 = 8,
adica numerele complexe cautate sunt z1 = 6 + 17i si
z2 = 6 + 8i.
vom avea y1 = 17 si y2 = 8,
adica numerele complexe cautate sunt z1 = 6 + 17i si
z2 = 6 + 8i.
3) a) Prin calcul direct, folosind i2 = -1, avem ca imagine punctul M( 21; -1)
b) Dupa amplificarea fractiei cu 3-2i si calculul direct se
obtine ca imagine un punct 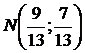
4) Pentru z = x+iy, avem 4(x2 + 2xyi - y2) + 8x2
+8y2 -3 = 0 ![]() 2xy = 0 si
2xy = 0 si
12x2 + 4y2 = 3. Daca x = 0 ![]()
![]() , iar daca y = 0
, iar daca y = 0 ![]()
![]() .
.
Deci numerele complexe cautate sunt: 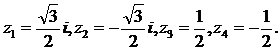
Functia data devine:![]()
a) Avem Im f(z) = 0 daca y = 0 ![]()
b) Daca Re f(z) = 0, atunci ![]()
a) x2 +2xyi - y2 =-5-12i ![]() xy = - 6 si x2 - y2 = -5
xy = - 6 si x2 - y2 = -5 ![]()
![]()
Deci avem solutiile: ![]()
b) Notam z2 = t ![]() t2 + 5t +4 = 0
t2 + 5t +4 = 0 ![]() t1 = -1 si t2 = -4, adica
solutiile ecuatiei sunt:
t1 = -1 si t2 = -4, adica
solutiile ecuatiei sunt:
![]()
c) z( z2 + 2z +3) = 0 ![]()
![]()
d) ![]() , adica
solutiile sunt:
, adica
solutiile sunt:
![]()
7) Daca α si ![]() sunt solutiile
ecuatiei z2 - z + 1 = 0
sunt solutiile
ecuatiei z2 - z + 1 = 0 ![]()
![]() si
si ![]() , iar
, iar ![]() . Astfel
. Astfel ![]()
8) Folosim scrierea in forma trigonometrica astfel:
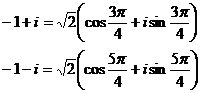
Numarul: ![]()
pentru ca ![]() ,
, ![]()
Daca z2 + z + 1 =0 ![]() z3 = 1
z3 = 1 ![]() zn = 1,
zn = 1, ![]() , atunci vom avea:
, atunci vom avea:
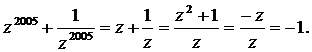
10) Daca ![]()
![]()
Presupunem ca ![]() si
si ![]() , atunci avem
, atunci avem ![]()
ceea ce contrazice relatia gasita anterior; deci avem ![]() sau
sau ![]() .
.
11) Solutia 1:
z є R ![]() b є R, cu z = b
, ceea ce conduce la (a-1)b + abi = 1+i
b є R, cu z = b
, ceea ce conduce la (a-1)b + abi = 1+i![]()
Deoarece a,b є R egalitatea de mai sus are loc ![]() (a-1)b = 1 si ab
=
(a-1)b = 1 si ab
= ![]() , de unde gasim a = 2 +
, de unde gasim a = 2 + ![]() .
.
Solutia 2:
![]() 12) Observam
ca:
12) Observam
ca:
![]() de unde daca se
folosesc puterile lui i, avem:
de unde daca se
folosesc puterile lui i, avem: ![]() .
.
a) Daca n = 1 ![]() . Daca n = 2
. Daca n = 2 ![]()
Fie n ≥ 3, se observa ca z = 0 este o solutie.
Presupunand ![]() si trecand la
module avem:
si trecand la
module avem: ![]() Atunci
Atunci ![]() , obtinand solutiile:
, obtinand solutiile: ![]()
b) Se scie ecuatia echivalenta : 1 - z + z2 - z3
++(-1)n-1zn-1 = 0, iar ![]()
rezulta 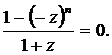
Daca n este par, avem de dat solutiile ecuatiei zn = 1, adica:
![]()
Daca n este impar, avem ecuatia zn = - 1, ce are solutiile:
![]()
c) 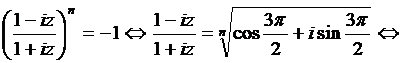
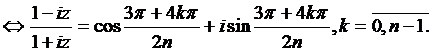
Notand ![]()
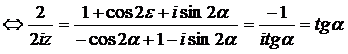 . Se obtin solutiile:
. Se obtin solutiile:
![]()
14) Folosin ipoteza![]()
![]()
![]()
![]()
![]() .
.
15) a) Daca z = = cost + isint, atunci:
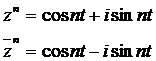
Prin adunarea acestor doua relatii rezulta 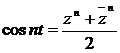 , iar prin scaderea lor avem
, iar prin scaderea lor avem  .
.
Observam, din ipoteza ca ![]() , adica
, adica 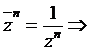
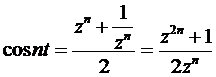 si
si 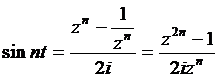
b) Fie z = cos200 + isin200, atunci z9 =
-1 si z18 = 1. folosind formulele demonstrate la punctul a)![]() , pentru n = 1, n = 2, respectiv n = 4. Expresia
cautata devine:
, pentru n = 1, n = 2, respectiv n = 4. Expresia
cautata devine:
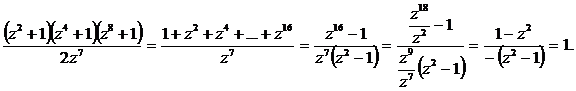
Deci ![]() = 1.
= 1.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4174
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved