| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Schema lui Bernoulli cu bila neintoarsa (hipergeometrica)
Se considera o urna ce
contine ![]() bile de doua culori, a
bile albe si b bile negre. Se extrag
bile din urna, una cate una, fara intoarcerea bilei in
urna. Vrem sa calculam probabilitatea ca din n bile extrase k sa fie de culoare alba.
bile de doua culori, a
bile albe si b bile negre. Se extrag
bile din urna, una cate una, fara intoarcerea bilei in
urna. Vrem sa calculam probabilitatea ca din n bile extrase k sa fie de culoare alba.
Pentru a calcula aceasta
probabilitate, folosim definitia clasica a probabilitatii.
Anume, exista ![]() posibilitati
de a extrage n bile din totalul celor
N cate sunt in urna la inceput.
Numarul cazurilor favorabile este dat de numarul modurilor de a
obtine k bile albe din cele a bile albe ce exista la inceput in
urna, adica
posibilitati
de a extrage n bile din totalul celor
N cate sunt in urna la inceput.
Numarul cazurilor favorabile este dat de numarul modurilor de a
obtine k bile albe din cele a bile albe ce exista la inceput in
urna, adica ![]() respectiv de numarul modurilor de a obtine
respectiv de numarul modurilor de a obtine ![]() bile negre din cele b bile negre cate exista in
urna la inceput si care este
bile negre din cele b bile negre cate exista in
urna la inceput si care este ![]() Avem astfel ca
probabilitatea
Avem astfel ca
probabilitatea ![]() de a se extrage k bile albe in n extrageri este data de formula
de a se extrage k bile albe in n extrageri este data de formula
![]()
Observatia 2.7. In mod
necesar avem ca ![]() si
si ![]() deci si
deci si ![]()
Exemplul 2.8. Intr-un lot de 50 de piese 10 sunt defecte. Se iau la intamplare 5 piese. Vrem sa calculam probabilitatea ca trei din cele cinci sa nu fie defecte.
Aceasta probabilitate se
calculeaza cu schema lui Bernoulli cu bila neintoarsa, unde ![]() si
si ![]() Astfel se obtine
ca
Astfel se obtine
ca
![]()
Observatia 2.9.
Daca in urna se afla bile de r
culori, anume ![]() de culoarea i, pentru
de culoarea i, pentru ![]() si se extrag n bile fa intoarcerea bilei extrase in
urna, atunci se obtine schema lui Bernoulli cu bila neintoarsa
cu mami multe stari.
si se extrag n bile fa intoarcerea bilei extrase in
urna, atunci se obtine schema lui Bernoulli cu bila neintoarsa
cu mami multe stari.
Probabilitatea ![]() , ca din cele n bile extrase
, ca din cele n bile extrase ![]() bile sa fie de culoarea i, pentru fiecare
bile sa fie de culoarea i, pentru fiecare ![]() se calculeaza cu formula
se calculeaza cu formula
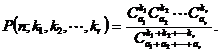
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 11700
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved