| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Numere complexe .
Forma algebrica :
- Expresia
z = a + bi .
se numeste forma algebrica a unui numar complex , unde a , b I R , i 2 = - 1
Elementele unui numar complex :
- numarul a se numeste partea reala a unui numar complex z ;
- grupul bi se numeste partea imaginara a unui numar complex z ;
- numarul b se numeste coeficientul partii imaginare ;
- numarul i se numeste unitatea imaginara , i 2 = - 1 .
Multimea numerelor complexe :
- Se noteaza cu :
C = .
Numere complexe egale :
- Fie numerele complexe :
z = a + bi si z' = a' + b'i
- Se spune ca :
z = z'
daca si numai daca
a = a' si b = b'
Suma numerelor complexe :
- Suma numerelor complexe z si z' este numarul :
z + z' = ( a + a' ) + ( b + b' )i .
Produsul numerelor complexe :
- Produsul numerelor complexe z si z' este numarul :
z z' = ( aa' - bb' ) + (ab' + a'b )i .
Numere complexe conjugate :
- Daca z = a + bi , z I C , atunci numarul :
![]()
se
numeste conjugatul
sau T ![]()
Proprietatile conjugatelor :
![]() 1). Un numar complex este real daca si numai daca este egal cu conjugatul
sau , adica :
1). Un numar complex este real daca si numai daca este egal cu conjugatul
sau , adica :
![]()
![]() 2).
2). ![]() si
si ![]() ( '
) z I C
( '
) z I C
![]() 3).
3). ![]() ( '
) z , z' I C
( '
) z , z' I C
![]() 4).
4). ![]() ( ' ) z , z' I C
( ' ) z , z' I C
![]() 5).
5). ![]() ( '
) z I C , ( '
) n I N*
( '
) z I C , ( '
) n I N*
Impartirea numerelor complexe :
- Pentru a imparti un numar complex cu un numar complex nenul se face o amplificare cu conjugatul impartitorului :

Modulul unui numar complex :
- Modulul numarului complex z = a + bi , este numarul real :
![]()
- proprietatile generale de la modulul unui numar real sunt valabile si in cazul modulului unui numar complex .
Rezolvarea ecuatiei de gradul al doilea :
- Fie ecuatia de gradul al doilea cu coeficienti reali :
![]()
care are discriminantul
![]() T
T
T ecuatia nu admite radacini reale
T admite radacini complexe
prin introducerea unitatii imaginare : i 2 = - 1
discriminantul devenind un numar pozitiv care permite extragerea radacini patrate
T

![]()
Exercitiul nr. 1 .
Sa se gaseasca numerele reale x si y din ecuatiile :
1). ![]() ; 2).
; 2). ![]() ;
;
3). ![]() ; 4).
; 4). ![]() ;
;
5). ![]() ; 6).
; 6). ![]() ;
;
7). ![]() ; 8).
; 8). ![]() ;
;
9). ![]() ;
;
10). ![]() ;
;
11). ![]() ;
;
12). ![]() .
.
Exercitiul nr. 2 .
Sa se calculeze :
1). ![]()
2). ![]()
3). ![]()
4). ![]()
5). ![]()
6). ![]()
7). ![]()
8). ![]()
9). ![]()
10). ![]()
11). ![]()
12). ![]()
13). ![]()
14). 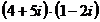
Exercitiul nr. 3 .
Sa se calculeze :
1). ![]()
2). ![]()
3). ![]()
4). ![]()
5). ![]()
6). ![]()
Exercitiul nr. 4 .
Sa se aduca la forma algebrica simpla , numerele :
1). ![]()
2). ![]()
5). 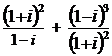
3). ![]()
4). ![]()
6). 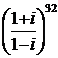
7). 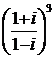
Exercitiul nr. 5 .
Sa se aduca la forma algebrica simpla , numerele :
1). 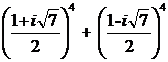 ; 2).
; 2). ![]() ;
;
3). ![]() ; 4).
; 4). ![]() ;
;
5). 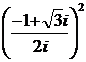 ; 6).
; 6). 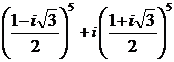 ;
;
7). 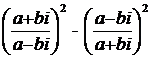 ; 8).
; 8). 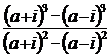 .
.
Exercitiul nr. 5 .
Sa se verifice egalitatile :
1). ![]() ; 2).
; 2). ![]() ;
;
3). 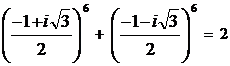 ; 4).
; 4). 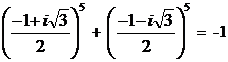 ;
;
5). 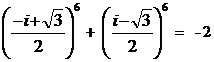 .
.
Exercitiul nr. 6 .
Determinati numerele complexe cu proprietatea :
![]()
Exercitiul nr. 7 .
Determinati
x , y I R , astfel incat : 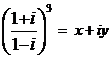
Exercitiul nr. 8 .
![]() si
si ![]()
Sa se calculeze :
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Exercitiul nr. 9 .
Sa se calculeze :
1). ![]() ; 2).
; 2). 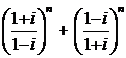 ;
;
3). 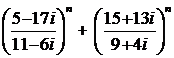 ; 4).
; 4). 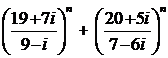 , unde n I N
, unde n I N
Exercitiul nr. 10 .
Sa se spuna care sunt conjugatele numerelor complexe si sa se calculeze modulele lor :
1). ![]()
2). ![]()
3). ![]()
4). ![]()
5). ![]()
6). ![]()
7). ![]()
8). ![]()
9). ![]()
10). ![]()
Exercitiul nr. 11 .
Fie ![]() ,
, ![]() . Calculati :
. Calculati : ![]() ,
, ![]() si
si
![]() .
.
Exercitiul nr. 12 .
Fie
numerele complexe : ![]() ,
, 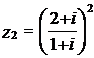 ,
, 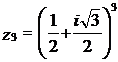
Determinati ![]() si
si ![]() unde k
= 1 , 2 , 3 .
unde k
= 1 , 2 , 3 .
Exercitiul nr. 13 .
Sa se calculeze ![]() daca
: z =
daca
: z = 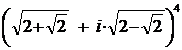
Exercitiul nr. 14 .
Sa se determine in fiecare caz in parte , numarul complex z astfel incat :
a). ![]() si
si ![]() ; b).
; b). ![]()
c). ![]()
Exercitiul nr. 15 .
Sa se determine z I C stiind ca :
a). ![]() si
si ![]() ; b).
; b). ![]() si
si ![]()
Exercitiul nr. 16 .
Sa se determine
numerele complexe z cu
proprietaea : ![]()
Exercitiul nr. 17 .
Sa se rezolve in C ecuatiile :
a). ![]()
b). ![]()
c). ![]()
d). ![]()
Exercitiul nr. 18 .
Sa se rezolve ecuatiile :
a). ![]()
b). ![]()
c). ![]()
d). ![]()
Exercitiul nr. 19 .
Sa se descompuna in factori de gradul intai trinoamele :
a). ![]()
b). ![]()
c). ![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2924
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved