Teoria selectiei

Teoria selectiei

Definitia Numim colectivitate sau populatie o multime de elemente care este cercetatǎ din punct de vedere a uneia sau mai multor caracteristici (proprietǎti), elementele colectivitǎtii numindu-se indivizi, iar numǎrul indivizilor unei colectivitǎti se va numi volumul colectivitǎtii.

Observatia 2. Din punct de vedere al teoriei probabilitǎtilor, o caracteristicǎ a unei colectivitǎti este o variabilǎ aleatoare , ale cǎrei caracteristici numerice se vor numi caracteristici teoretice. Astfel vom avea media teoreticǎ, dispersia teoreticǎ, s.a.m.d.

Observatia 3. Problema centralǎ a statisticii matematice este stabilirea legii de probabilitate pe care o urmeazǎ caracteristica .

Observatia 4. Dupǎ cum variabila aleatoare este de tip discret, respectiv de tip continuu vom avea caracteristici de tip discret, ca de exemplu numǎrul copiilor dintr-o familie, si caracteristici de tip continuu, ca de exemplu rezistenta la rupere a unui fir de mǎtase. De asemenea, dacǎ proprietatea cercetatǎ este calitativǎ, ca de exemplu culoarea ochilor, vom numi caracteristica respectivǎ atribut.

Definitia 5. Numim selectie (sondaj) o subcolectivitate a colectivittii cercetate , iar numǎrul indivizilor ce intrǎ in selectie se numeste volumul selectiei (sondajului).

Definitia 6. O selectie se numeste repetatǎ sau bernoullianǎ, dacǎ dupǎ examinarea individului, acesta este reintrodus in colectivitate, in caz contrar, adicǎ dacǎ individul examinat nu se reintroduce in colectivitate, vom spune cǎ selectia este nerepetat

Observatia 7. Dacǎ volumul colectivitǎtii este mult mai mare decat volumul selectiei, atunci selectia nerepetatǎ poate fi consideratǎ ca fiind selectie repetatǎ. In cele ce urmeazǎ, vom considera numai selectii repetate.

Definitia 8. Numim date de selectie relative la caracteristica , valorile obtinute pentru caracteristica privind indivizii care intrǎ in selectie. Dacǎ selectia este de volum , vom nota datele de selectie prin , ,,

Observatia 9. Datele de selectie , ,, sunt valori ale unor variabile aleatoare, respectiv , ,, care se vor numi variabile de selectie.

Observatia 10. Dacǎ selectia este repetatǎ, atunci variabilele de selectie , ,, sunt variabile aleatoare independente si urmeazǎ fiecare aceeasi lege de probabilitate cu variabila aleatoare , adicǎ sunt identic repartizate cu .

Observatia 1 Dacǎ datele de selectie , ,,au valorile,, ,, atunci tabloul de forma

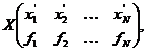
unde este frecventa aparitiei valorii , se va numi distributia empiricǎ de selectie a caracteristicii

Observatia 12. Dacǎ este de tip continuu, se face o grupare a datelor de selectie in clase prin impǎrtirea intervalului , unde ia valori, in subintervalele date prin

Distributia empiricǎ de selectie a caracteristicii va fi de aceeasi formǎ ca si in cazul discret

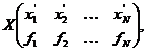
unde, de regulǎ, iar este frecventa datelor de selectie din intervalul (clasa)

Observatia 13. De multe ori este necesarǎ o grupare a datelor de selectie pentru cazul cand caracteristica este de tip discret. De exemplu, dac reprezintǎ salariile angajatilor unei unitti comerciale.

Definitia 14. Dacǎ avem functia numim functie de selectie sau satatisticǎ, variabila aleatoare , ,, fiind variabilele de selectie, iar valoarea numericǎ o numim valoarea functiei de selectie, , ,, fiind datele de selectie.

Definitia 15. Numim medie de selectie functia de selectie datǎ prin

iar valoarea numericǎ

o numim valoarea mediei de selectie.

Observatia 16. Dacǎ se considerǎ caracteristica care urmeazǎ legea normalǎ , atunci media de selectie urmeazǎ legea normalǎ

Observatia 17. Dacǎ se considerǎ caracteristica care urmeazǎ legea normalǎ , atunci statistica datǎ prin

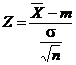
urmeazǎ legea normalǎ

Intr-adevǎr, deoarece intre si existǎ o legǎturǎ liniarǎ, avem, pe baza observatiei precedente, cǎ si variabila aleatoare urmeazǎ legea normalǎ. dar avem cǎ

si

de unde rezultǎ ca statistica urmeazǎ legea normalǎ

Observatia 18. Dacǎ avem caracteristicile independente si , care urmeazǎ fiecare legea normalǎ, respectiv si , atunci statistica

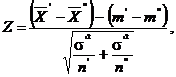
unde si sunt mediile de selectie date respectiv prin variabilele de selectie , ,, si , ,, relative la caracteristicile si , urmeazǎ legea normalǎ

Definitia 19. Se numeste moment de selectie de ordin , functia de selectie

, iar valoarea numericǎ o numim valoarea momentului de selectie de ordin .

Observatia 20. Pentru , avem cǎ

Definitia 2 Numim moment centrat de selectie de ordin , functia de selectie

iar valoarea numericǎ .

o numim valoarea momentului centrat de selectie de ordin

Observatia 22. Dacǎ se considerǎ caracteristica care urmeazǎ legea normalǎ , atunci statisticile

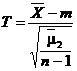si

urmeazǎ respectiv legea Student cu grade de libertate si legea cu grade de libertate.

De asemenea, considerand functia de selectie

numitǎ dispersie de selectie, se obtine c

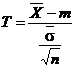si

Observatia 23. Momentul centrat de selectie de ordin , pentru , urmeazǎ legea normalǎ unde si sunt momentele teoretice de ordin si respectiv

Definitia 24. Numim functie de repartitie de selectie, functia de selectie definitǎ prin

pentru orice

unde noteazǎ numǎrul variabilelor de selectie mai mici decat

Exemplul 25. Functia de repartitie de selectie pentru distributia empiricǎ de selectie

este datǎ prin

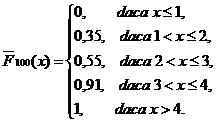
Teorema 26 (Glivenko). Dacǎ se considerǎ caracteristica ce are functia de repartitie teoreticǎ si fie functia de repartitie de selectie , atunci

Corolarul 27 (Kolmogovor). Fie caracteristica de tip continuu, care are functia de repartitie teoreticǎ si fie functia de repartitie de selectie , iar atunci

pentru

Observatia 28. Functia se numeste functia lui Kolmogovor si se aflǎ tabelatǎ in Anexa V.