Aristotel (Viata si opera)

Aristotel (Viata si opera)

1. Viata lui Aristotel

Aristotel s-a nascut in 384 i.H. (anul 1 al Olimpiadei a 90-a), in Stagira - oras in peninsula Chalcis, la granita cu Macedonia (din acest motiv, Aristotel este supranumit Stagiritul). Tatal sau, medicul Nicomah, provenea dintr-o familie venita in regiune din Mesenia, in secolul VIII sau VII i. Hr. Nicomah era un om cultivat, medic al regelui Filip al Macedoniei si autor a doua lucrari literare. Mama sa, Phaetis, era din Stagira, lucru demonstrat si prin retragerea pentru scurta vreme (in 340 i.H) a lui Aristotel - cand a fost atacat de dusmanii sai politici - pe o proprietate din Stagira, mostenire materna.

Aristotel isi incepe educatia sub instruirea tatalui sau, iar dupa ce ramane orfan de ambii parinti, sub directa indrumare a rudei sale Proxenos.

La varsta de 17 ani pleaca la Atena, unde timp de doua decenii este membru al Academiei platonice, intai ca elev, apoi ca profesor, pana la moartea lui Platon (347 i.H). In aceasta perioada devine cunoscut ca autor a numeroase lucrari si cursuri tinute in cadrul Academiei. Dupa moartea lui Platon, Aristotel traieste catva timp in Assos (regatul Misia - Asia Mica), la curtea tiranului Hermias (cu a carui nepoata, Pythias, se casatoreste) si in Mytilane.

Apoi, in 343 i.Hr., Aristotel este chemat la Pella, la curtea regelui Filip al Macedoniei, ca sa se ocupe de educatia fiului acestuia, Alexandru. In scrisoarea in care regele ii propunea sa fie educatorul fiului sau, scria: 'Am un fiu, dar multumesc mai putin zeilor ca mi l-au dat, cat mai ales ca ei au facut ca el sa se nasca in timpul tau. Sper ca grija ta si vederile tale il vor face demn de mine si de viitoarea sa tara'.

Dupa ce Alexandru ajunge rege al Macedoniei (336 i.H) si impune o pace intre cetatile grecesti, Aristotel se intoarce in Atena si, impreuna cu prietenul si discipolul sau Teophrast, intemeiaza o scoala filozofica proprie, numita 'Lykeion' (Liceul) sau 'peripatetica' (deoarece filozoful obisnuia sa filozofeze plimbandu-se cu elevii sai).

Gallius relateaza ca in aceasta scoala Aristotel tinea dimineata conferinte acromatice, destinate ascultatorilor mai avansati, iar dupa pranz conferinte exoterice (retorice-populare) pentru publicul mare. Invatatura exoterica se referea la studiile de retorica - la arta de a argumenta si la stiinta politica. Invatatura acromatica avea un obiect mai profund si mai subtil - fizica si problemele de logica .

Datorita familiei regale macedonene care l-a sustinut, Aristotel a reusit sa infiinteze o biblioteca foarte bine dotata cu carti din toate domeniile stiintei epocii sale.

Pe plan familial, Aristotel se casatoreste de doua ori. Prima sotie este Pythia, de la care a avut o fata ce purta numele mamei si pe care, cand isi intocmeste testamentul, o destineaza ca sotie lui Nicanor, fiul lui Proxenos, primul sau tutore - educator. Pythia, sotia, a murit, probabil imediat dupa intoarcerea lui Aristotel la Atena, in 335 i.H. sau, eventual, in timpul vreunei calatorii in aceasta cetate. Asta se deduce din testamentul lui in care stabileste ca osemintele primei sotii sa fie asezate in acelasi mormant cu ale sale, ceea ce poate sa insemne ca ele se aflau undeva in preajma Atenei. Cu a doua sotie (nenominalizata in documente), Aristotel are un baiat Nicoimachos, caruia ii dedica una din operele sale.

Aristotel conduce Lykeion timp de 12 ani (335-322 i.Hr.). Din pricina mortii lui Alexandru (323 i.Hr.), el este silit sa plece din Atena, fiind acuzat - ca si Socrate - de 'asebie'. Se spune ca, cu aceasta ocazie, el ar fi zis: 'Nu voi mai da prilej atenienilor ca sa pacatuiasca a doua oara impotriva filozofiei'. Lykeyon continua sa existe vreme de cateva secole dupa moartea lui Aristotel.

Refugiat la Chalkis in insula Eubeea, Aristotel moare dupa un an (322 i.Hr.). Asupra sfarsitului sau au existat felurite versiuni printre autorii vechi. Unii spuneau ca s-ar fi otravit de teama continuarii unui proces, in care, desi Aristotel era intemeietorul logicii, nu se putea apara deoarece nu era ascultat de catre instanta; altii - ca s-ar fi aruncat in canalul Eurit care separa Eubeea de restul Greciei, disperat ca nu poate sa explice mareele, fenomen foarte sensibil in acest punct al Mediteranei. Cel mai probabil insa, se pare ca Aristotel a murit de pe urma unei maladii stomacale, de care suferise toata viata .

2. Opera lui Aristotel

Opera lui Aristotel are o istorie foarte interesanta. Aristotel si-a lasat manuscrisele prin testament lui Teofrast care - la randul lui - le-a lasat unui oarecare Nelsus, un elev al lui Aristotel. Strabo istoriseste ca, pentru a le salva de furia de colectionar a printului de Pergamon, opera aristotelica a trebuit sa fie ascunsa intr-o pivnita umeda, unde a zacut 13 ani; de acolo a fost adusa abia pe la 100 i.H. la Atena, iar de aici, prin Sulla, la Roma. Aceasta relatare priveste numai manuscrisele lui Aristotel, fiindca in secolul al III-lea i.H. operele acestuia erau cunoscute. In 50 i.H. a aparut la Roma o editie noua a tuturor lucrarilor aristotelice, sub ingrijirea lui Andronicos din Rhodos. Aceasta editie constituie temeiul traditiei aristotelice. Ea a aparut intai in limba latina, cu un comentariu al arabului Averroes, in Venetia (1489), apoi in limba greaca (1495). Dupa aceea studiul filozofiei aristotelice a fost neglijat pana in secolul al XIX-lea, cand incepe sa renasca iarasi. In acest secol, cea mai completa editie a operelor aristotelice o constituie editia Academiei de stiinte din Berlin, care a aparut in 5 volume (1831-1870). Apoi a aparut marea editie a aceleiasi Academii, a Comentariilor grecesti (Commentaria in Aristotelem Graeca) in 23 de volume si 3 volume supliment. O alta editie a textelor aristotelice, insotite de un aparat critic, a fost publicata in 'Bibliotheca Teubeneriana'.

Ce trebuie retinut este vastitatea operei aristotelice, realizata intr-o perioada relativ scurta. Dupa caracteristica literara, aceasta opera se imparte in trei mari grupe.

 1.  Lucrarile editate de Aristotel insusi. Acestea au o forma dialogica si isi au originea in epoca in care Aristotel apartinea Academiei platonice. Din nefericire ele s-au pierdut, nemai ramanand decat cateva fragmente razlete.

 2.  Colectii facute cu ajutorul elevilor sai pentru a fi folosite ca material didactic in 'Lykeion'. Acestea cuprindeau domenii diverse. Este instructiva in aceasta privinta lucrarea  'Constitutia ateniana' gasita si editata in 1892 de Kaibel si Wilamowitz, care n-ar fi decat o parte dintr-o opera monumentala ce purta titlul "Politeia".

3.  Lucrari pur stiintifice. Acestea s-au pastrat in intregime si au forma unor prelegeri, avand adesea neglijente stilistice si exprimari obscure, explicabile prin moartea neasteptata a autorului, care l-a impiedicat de a le da o forma finala. Aceste scrieri se impart in:

a)   Scrieri cu caracter logic ce au fost adunate in epoca bizantina sub titlul Organon (unealta spirituala). Aici sunt grupate: 

- Categoriile (moduri ale existentului);

- Analitica priora (despre silogisme) si Analitica posteriora (despre argumente, definitii si impartiri);

- Peri arimineias (De interpretatione, despre principiu si judecata);

- Topica (un fel de indreptare pentru arta de a discuta, precum si o colectie a sofismelor, pe care Aristotel le combate, descoperindu-le erorile logice).

 b) Scrieri din domeniul stiintelor  naturii: Fizica (in 8 carti), Despre cer (4 carti), Despre nastere si disparitie (2 carti), Meteorologie (4 carti), Despre suflet (3 carti), Istoria mare a animalelor (10 carti) si asa-zisa Parva naturalia.

c)   Scrieri etice. Opera principala este Etica Nichomachiana (in 10 carti), numita asa dupa Nicoimachos, fiul lui Aristotel. Eudemos, un elev al lui Aristotel, a preluat aceasta etica care s-a afirmat sub numele de Etica Eudemica. In afara de acestea, mai este cunoscuta o a treia etica, prelucrare a celorlaltor doua anterioare, cunoscuta sub numele de Etica mare (Magna moralia). Aristotel a mai scris si o lucrare de etica practica sau aplicata, cu titlul Politica (in  8 carti), care a ramas neterminata. Tot aici se mai poate aminti un dialog 'Eudemos', care s-a pierdut.

 d) Scrieri din domeniul esteticii: Retorica (in 3 carti) si Poetica.

 e) Scrieri cu caracter filozofic general: Metafizica (in 14 carti).

3. Logica aristotelica

Aristotel este considerat a fi parintele logicii ca stiinta, iar cele 6 scrieri de logica ale sale (Categoriile, Despre interpretare, Analitica Prima, Analitica Secunda, Topica, Respingerile Sofistice), reunite mai tarziu in Organon, sunt considerate a fi primul tratat de logica.

Ca un detaliu interesant, ceea ce intelegem astazi prin Logica aristotelica, Aristotel ar fi numit Analitica. Pentru logica, el folosea termenul de Dialectica. Este posibil ca multe din lucrarile atrubuite lui Aristotel sa nu fi fost autentice, pentru ca cea mai mare parte a lor au fost editate de elevi si colaboratori ai sai. Aceste lucrari au fost aranjate in forma actuala (6 carti) cam prin secolul 1 i.H. Inafara lor mai exista un volum al lui Aristotel referitor la logica, inclus in a patra carte din Metafizica.

3.1. Termeni

In logica aristotelica, o propozitie este formata dintr-un subiect si un predicat. Un subiect sau un predicat este numit termen. Subiectul are atasata o proprietate cantitativa, iar el impreuna cu aceasta proprietate se numeste subiect gramatical. Un subiect poate fi universal sau particular. De exemplu, "Toate planetele" este un subiect gramatical universal, pe cand "Unele planete" este un subiect gramatical particular.

Proprietatea cantitativa a unui subiect este particulara cand caracterizeaza o submultime a multimii subiectilor. Predicatele pot fi numai universale; orice constructie gramaticala este numita predicat gramatical.

De exemplu:

Unii greci sunt oameni puternici.

Aici "greci" este subiect, "Unii greci" este un subiect gramatical particular, "oameni" este predicat, "sunt oameni puternici" este predicat gramatical.

Subiectele si predicatele se pot interschimba (un subiect dintr-o propozitie poate fi predicat in alta). Astfel

Unii oameni puternici sunt greci.

este de asemenea o propozitie.

Pentru a asigura aceasta posibilitate de interschimbare, Aristotel exclude din logica sa termenii singulari.

Termeni singulari:

Exemple de termeni singulari pot fi "Socrate", "Platon", "Xenocrate". Termenii singulari nu pot avea proprietati cantitative universale; nu se poate spune de exemplu "Toti Platon" (Platon este considerat ca individ unic). Aristotel a enuntat dicotomia: "Unele lucruri sunt universale, altele sunt individuale" ca un element de baza al logicii, detaliind: "Un lucru este universal daca poate fi folosit si drept predicat pentru mai multi subiecti, iar un lucru este individual daca nu poate fi utilizat ca predicat".

In consecinta, toti termenii singulari - si deci toate propozitiile singulare - sunt ignorate de logica aristotelica (fapt considerat de logicieni ca un punct slab al acestei constructii).

3.2. Propozitii

Asa cum am spus mai sus, o propozitie este formata din doi termeni: un subiect gramatical si un predicat gramatical. De asemenea, o propozitie are doua proprietati: calitate si cantitate. Calitatea unei propozitii este afirmativa (predicatul este afirmat de catre subiect) sau negativa (predicatul este negat de catre subiect). Deci vor exista doua tipuri de propozitii: afirmative si negative.

Cantitatea unei propozitii este universala sau particulara; deci exista propozitii universale si propozitii particulare.

Din combinarea lor, in logica aristotelica exista patru tipuri de propozitii:

Codurile A, E, I, O provin din vocalele cuvintelor latine affirmo si nego. Pentru a le tine minte se foloseau versurile (scrise in latina):

Asserit A, negat E, verum generaliter ambo;
Asserit I, negat O, sed particulariter ambo.

Alte tipuri de propozitii nu exista in logica aristotelica.

O tabela care compara propozitiile din logica moderna a predicatelor cu propozitiile din logica aristotelica:

Codurile difera putin de cele din tabela anterioara, iar S si P marcheaza subiectul, respectivul predicatul propozitiilor.

Patratul opozitiilor:

Relatia dintre propozitii im logica aristotelica este analizata sugestiv folosind un patrat al opozitiilor. Doua propozitii cu acelasi subiect si acelasi predicat sunt opuse daca difera prin cel putin unul din cele doua atribute ale lor. De exemplu: "Toti oamenii sunt muritori." si "Unii oameni sunt muritori." sunt propozitii opuse.

Exista mai multe tipuri de propozitii opuse. Astfel:

Doua propozitii sunt alternative daca ele difera numai prin atributul calitate (de exemplu: "Toti S sunt P" si "Unii S sunt P").

Doua propozitii universale sunt contrare daca difera numai prin atributul calitate (de exemplu: "Toti S sunt P" si "Nici un S nu este P").

Doua propozitii particulare sunt sub-contrare daca daca difera prin atributul calitate (de exemplu "Unii S sunt P" si "Unii S nu sunt P").

Doua propozitii sunt contradictorii daca difera prin ambele atribute (de exemplu: "Nici un S nu este P" si "Unii S sunt P". Sau: "Toti S sunt P" si "Unii S nu sunt P").

Aceste relatii de opozitie sunt reliefate prin urmatoarea diagrama (prezentata in Stanford Encyclopedia of Philosophy: Traditional Square of Opposition):

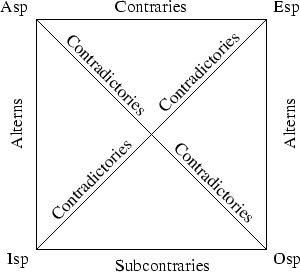
Constructia nu a fost realizata de Aristotel; ea a fost prezentata prima oara in secolul II A.D. de Boetius, folosind direct definitiile lui Aristotel.

Propozitii singulare:

In logica aristotelica nu exista propozitii singulare. Propozitii cum ar fi "Socrate este un om" nu pot fi prezente aici. Deci constructia

Toti oamenii sunt muritori.

Socrate este om.

Deci Socrate este muritor.

nu a fost niciodata elaborata (sau acceptata) de Aristotel, ea nefiind un silogism aristotelic.

3.3. Silogisme:

Un silogism aristotelic este format din doua ipoteze (premise) si o concluzie care rezulta ca un caz particular din aceste ipoteze. Atat premisele cat si concluzia sunt propozitii de tipul A, E, I, O.

Teminologie (definita de Aristotel): :

Ipotezele contin un termen comun, numit termen mijlociu. Ceilalti termeni ai ipotezelor sunt numiti termeni extremi.

Predicatul concluziei este un termen major, iar subiectul concluziei este un termen minor.

Ipoteza care contine termenul minor se numeste premiza minora; similar, ipoteza care contine termenul major se numeste premiza majora.

Un exemplu:

Aici termenul "muritori" este major, "grecii" - minor, iar "oameni" este termenul mijlociu.

Ordinea prezentarii ipotezelor nu este importanta pentru Aristotel; Jan Lukasiewicz arata insa ca unele deductii filozofice care nu se pot explicate rational a condus pe unii comentatori ai operei aristotelice la concluzia ca premiza majora trebuie sa fie prima, premiza minora a doua, iar concluzia - ultima.

Aristotel imparte silogismele in doua categorii:

Silogisme perfecte "care nu necesita nimic altceva atunci cand sunt enuntate pentru a trage concluzia".

Silogisme imperfecte: "necesita una sau mai multe propozitii care sunt consecinte ale termenilor, dar nu au fost enuntate ca ipoteze".

Silogismele perfecte nu sunt demonstrabile; in logica aristotelica ele sunt luate ca axiome si folosite ulterior - cu operatia de conversie - pentru a demonstra silogismele imperfecte.

Conversia:

Conversia este procesul de inter-schimbare a subiectului cu predicatul dintr-o propozitie, pastrand calitatea.

Sunt doua tipuri de conversie:

conversia simpla, unde atributul cantitate este neschimbat, si

conversia morfologica (per accidens), unde atributul cantitate este schimbat de la universal la particular.

Nu toate conversiile sunt valide, iar unele conversii nici nu exista. Prezentam un tabel al conversiilor posibile din logica aristotelica:

Observatii:

1. Aristotel accepta conversia morfologica Asp Ips dar nu si o conversie simpla Asp Aps, spunand: "termenii unei afirmatii trebuie sa fie convertibili, dar nu universal ci numai particular". Mai mult, el da un exemplu de conversie corecta: "Daca tot ce este placut este bun, atunci ceva bun trebuie sa fie placut".
2. Conversiile Esp Eps si Esp Ops sunt corecte. Iata demonstratia lui Aristotel pentru conversia simpla Esp Eps:

Daca nici un B nu este A, atunci nici un A nu poate fi B. Daca un A (sa spunem C) ar fi B, atunci nu ar mai fi adevarat ca nici un B nu este A (pentru ca C este B).

3. Arata conversia simpla Isp Ips si da numeroase exemple de conversii nevalide. Celebru este exemplul lui Aristotel ca particularul negativ nu admite conversie simpla (Osp nu se transforma in Ops): "Daca unele animale nu sunt oameni, asta nu inseamna ca unii oameni nu sunt animale".
4. Pentru ca o conversie morfologica sa fie valida, trebuie sa existe o ipoteza suplimentara: aceea ca in universal discursului exista cel putin un element. Multe atacuri si controverse referitoare la logica aristotelica se bazeaza pe aceasta problema: ce se intampla daca universal discursului este vid.

Cele patru figuri:

Pozitia termenului mijlociu in premise conduce la asa numitele figuri. Figurile definesc asezarile posibile ale termenului mijlociu intr-un silogism. Daca notam cu M termenul mijlociu, cu P termenul major si cu S termenul minor, exista patru variante posibile, definite prin 4 figuri:

Figura 1 este deductia (conform gandirii aristotelice), cea mai apropiata de rationamentul natural. Deci ea va genera numai silogisme perfecte.

De remarcat ca Figura 4 nu a fost definita explicit in lucrarile lui Aristotel, desi acesta a acceptat rationamente deductibile din aceasta figura. Figura 4 este numita adesea figura Galeniana, deoarece se pare ca cel care a folosit-o primul a fost Galenus (131 - 201 A.D.).

3.4. Reprezentari silogistice:

Reprezentarea unui silogism este o secventa de propozitii si concluzii. Figurile asociate unei reprezentari compun un silogism. Silogismele valide, cu figurile si reprezentarile asociate sunt stranse in tabelul:

Tabela urmatoare da reprezentarile silogistice valide derivate din Figura 1. Asa cum s-a afirmat anterior, aceste silogisme sunt perfecte.

Desi toate sunt silogisme perfecte, pentru Aristotel cele mai clare sunt Barbara si Celarent. Silogismele Darii si Ferio sunt deduse abia in ultima sa lucrare.

Mnemonica da reprezentarile valide, prin vocalele din cuvantul care reprezinta silogismul. Astfel, Barbara semnifica AAA, Celarent - EAE, Darii - AII si Ferio - EIO.

Deci, din informatia ca Barbara este un silogism din Figura 1, se deduce imediat forma sa.

Acest silogism se poate scrie:

Daca toti M sunt P
si toti S sunt M

atunci toti S sunt P.

unde plasarile lui M, P si S corespund Figurii 1:

Pentru a memora din ce figura este derivata fiecare reprezentare silogistica, logicienii din Evul Mediu au construit versuri. De exemplu:

Barbara, Celarent, Darii, Ferio - que prioris.
Cesare, Camestres, Festino, Baroko, secundae.
Tertia Darapti, Disamis, Datisi, Felapton,
Bocardo, Ferison habet. Quarta insuper addit
Bramantip, Camenes, Dimaris, Fesapo, Fresison.

Detaliind, reprezentarile silogistice din Figura 2 (deduse din al doilea vers) sunt listate in tabelul urmator (de mentionat ca toate sunt silogisme imperfecte):

Deoarece sunt imperfecte, ele trebuie demonstrate. Iata cum demonstreaza Aristotel validitatea silogismului Cesare:

Deci Cesare este o reprezentare silogistica valida.

Rationamentul ilustrat mai sus este numit reducere; premisele si concluzia unui anumit argument sunt transformate intr-un silogism din Figura 1, deducand de aici ca argumentul este valid.

Reprezentarile silogistice din Figura 3 sunt listate mai jos; de asemenea, si acestea sunt imperfecte.

Mnemonicele contin mai multa informatie decat simpla reprezentare silogistica. Astfel:

i.            Mnemonicele din Figurile 2 - 4 au ca prima litera B, C, D sau F, indicand prin aceasta reprezentarea silogistica din Figura 1 la care se reduce silogismul pentru a-i demonstra validitatea (de exemplu Felapton se va reduce la Ferio).

ii.          Daca un `c' urmeaza dupa un `o', atunci demonstratia se face prin reducere la absurd. Jan Lukasiewicz arata ca sunt doua astfel de silogisme (Bocardo si Baroco) care nu sunt demonstrate corect de Aristotel. Detalii se gasesc in: Jan Lukasiewicz , Aristotle's Syllogistic, From the Standpoint of Modern Formal Logic, capitolul 17.

iii.        Daca un `s' (sau `p') urmeaza dupa prima sau a doua vocala, atunci propozitia corespunzatoare acestei vocale suporta, in cursul demonstratiei, o conversie (simpla sau morfologica).

iv.        Daca un `s' (sau `p') urmeaza dupa ultima vocala, atunci concluzia se obtine printr-o conversie (simpla sau morfologica) din concluzia silogismului din Figura 1 folosit in operatia de reducere.

v.          Aparitia literei `m' indica o rearanjare a premiselor, pentru a respecta ordinea: premisa majora, premisa minora, concluzie.

Reprezentarile silogistice din Figura 4 sunt:

Si acestea sunt toate imperfecte.

Demonstrarea validitatii silogismelor imperfecte poate fi data folosind regulile asociate mnemonicelor.

Sa exemplicam aceasta cu silogismul Dimaris. Vocalele sale sunt I, A, I; deci se va demonstra silogismul Ipm & Ams Isp.

Deoarece Dimaris incepe cu litera D , se efectueaza o reducere la silogismul Darii din Figura 1. Litera `s' dupa ultima vocala indica o conversie simpla a concluziei silogismului Darii. In plus, litera `m' indica o reordonare a premiselor.

Detaliile demonstratiei sunt:

4. Incheiere

O discutie despre viata si - mai ales - opera lui Aristotel poate continua in mai multe articole. Am prezentat aici numai o mica deschidere, incercand o abordare cat mai generala asupra logicii aristotelice. Evident, se poate continua cu detalieri despre paradoxurile acestei logici, despre criticile care se aduc (si care au condus la alte abordari axiomatice ale logicii), despre transpuneri ale acestei logici in diverse domenii - filozofie, etica, matematica etc etc.

Pentru articolul de fata am folosit lucrarile:

1. Yann Lamontagne - Aristotelian Logic, Planet.Math.org
2. Stanford Encyclopedia of Philosophy: Traditional Square of Opposition
3. Stanford Encyclopedia of Philosophy: Aristotle's Logic
4. Wikipedia : Aristotelian Logic
5. Wikipedia: Term Logic

O sursa a operelor lui Aristotel (traduse in engleza) poate fi https://classics.mit.edu

Bibliografie extinsa (fara a fi completa):

1. A.,Dumitru - Istoria logicii, E. D. P, Bucuresti, 1975, p331-339

2. I. Didilescu, P. Botezatu - Teoria clasica si interpretarile moderne, E.D.P, Bucuresti, 1976

3.  M. A. Marica, Logica generala, Ed.Muntenia, Constanta, 2005

4. M. Florian - Logica si epistemologie, Ed.Antet,Oradea, 1996

5. N. Ionescu - Curs de istorie a logicii, Ed.Humanitas, Bucuresti, 1993

6. *** Probleme de logica, Ed. R.S.R, Bucuresti, 1968

7.  *** Logica,sub redactia lui D.P.Gorski, P.V.Tavanet, Ed.Stiintifica,Bucuresti, 1957

8. Constantin Noica, Pentru o interpretare a categoriilor la Aristotel, Ed.Academiei. Bucuresti, 1968

9. Anton Dumitriu, Logica lui Aristotel, in Istoria logicii, Ed.Tehnica, Bucuresti, 1993

10. Alberto Jori, Aristotele, ed. Bruno Mondadori, Milano 2003.

11. Sorin Vieru, Inceputuri de semantica logica la comentatorii antici ai 'Categoriilor' , Ed. Academiei, Bucuresti, 1972

12. Mircea Florian, Cosmologia elena in 'Revista de filozofie', nr.1,2,3/1929

13. Elena Anghel, Substanta si devenire la Aristotel, in 'Revista de filozofie', nr.2/1995

14. Gheorghe Vladutescu, Experienta si inductie la Aristotel, Ed.Stiintifica si Enciclopedica, Bucuresti, 1975

15. W.Windelband, Istoria filozofiei grecesti, Ed. Moldova, Iasi, 1995

16. Martin Heidegger, Despre esenta si conceptul lui ΦYΣΙΣ, in 'Repere pe drumul gandirii', Ed.Politica, Bucuresti, 1988

17. The Internet Encyclopedia of Philosophy: Aristotle. https://www.utm.edu/research/iep/a/aristotl.htm

18. Lukasiewicz, Jan: Aristotle's Syllogistic, From the Standpoint of Modern Formal Logic. Clarendon Press. Oxford, 1951

19. Parry, William T., Hacker, Edward A.: Aristotelian Logic. State University of New York Press. Albany, 1991

20. Parsons, Terence: Stanford Encyclopedia of Philosophy: Traditional Square of Opposition. https://plato.stanford.edu/entries/square/

21. Rose, Lynn E.: Aristotle's Syllogistic. Charles C Thomas Publisher, Springfield, 1968

22. Smith, Robin: Stanford Encyclopedia of Philosophy: Aristotle's Logic https://plato.stanford.edu/entries/aristotle-logic/

23. Wikipedia: Aristotle. https://en.wikipedia.org/Aristotle

24. Wikipedia: Aristotelian Logic. https://en.wikipedia.org/Aristotelian_logic