| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
| електронен | изкуство култура | икономика | история | книга | компютри | медицина | психология |
| различни | социология | техника | управление | финанси | химия |
DOCUMENTE SIMILARE |
|
![]()
![]()
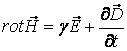 (8)
(8)
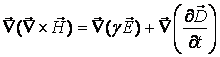 (9)
(9)
![]() (10)
(10)
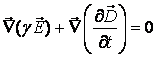 (11)
(11)
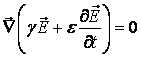 (12)
(12)
![]() и
следователно
уравнение (11)
може да се
запише във
вида
и
следователно
уравнение (11)
може да се
запише във
вида
![]() (13)
(13)
![]() (14)
(14)
![]()
![]() (
(
![]() (16)
(16)
![]() (17)
(17)
![]() (1
(1
получи разпределението на електрическия потенциал в разглеждата област трябва да се реши уравнение (18) с МКЕ.
FEMM F MM current flow problems
Ако
полето се
възбужда от
постоянен
електрически
ток, чиято
честота е
нула, членът ![]()
![]() (19)
(19)
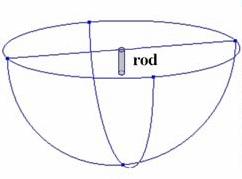
Решението на задачата става в двумерния случай със свободния пакет за анализ по МКЕ - FEMM lecnet
значителни изчислителни ресурси на компютъра както и време за което се решава задачата.
|
|
|
|
|
|
V
D V
Impedance boundary condition
File New
Create new problem Current flow
O File Save as Grounding rod
Problem От “Problem type” се избира, а от “Units” –“milimeters”.
Problem
Problem type Axisimmetric
Frequency Hz
Depth a
Length Units ilimeters
Solver Precision e
Min angle
Comment (коментар) – например, записва се Electric field of grounding rod.
Създаване геометрията на модела
![]() на 1, което
означава, че
разстоянието
между две съседни
точки от
мрежата ще
бъде 1 mm snap to grid
на 1, което
означава, че
разстоянието
между две съседни
точки от
мрежата ще
бъде 1 mm snap to grid ![]() от
вертикалната
лента с
инструментите.
Snap to grid
от
вертикалната
лента с
инструментите.
Snap to grid
Point ![]()
lines ![]()
Arc Segment ![]() OY OX Angle Max Segment Degrees
OY OX Angle Max Segment Degrees
View Natural
не е част от модела за него не се задава материал.
![]()
![]() m Properties Materials Property Definition Add Materials Block Property Name New Material Soil
m Properties Materials Property Definition Add Materials Block Property Name New Material Soil ![]() и
и ![]() Electrical conductivity s m
Electrical conductivity s m ![]() и
и ![]() със
стойности
единица.
Щраква се
върху ОК
и се излиза
от прозореца.
С това е
дефиниран
нов материал
–почва.
със
стойности
единица.
Щраква се
върху ОК
и се излиза
от прозореца.
С това е
дефиниран
нов материал
–почва.
Block Labels ![]() от лентата
с
инструментите
и се
позиционира един
блоков
етикет
(зелена
точка) за
областта на
почвата.
Щраква се с
десен бутон
върху възела
на блоковия
етикет, така
че възелът да
стане червен,
което е
признак, че
този възел е
избран.
Натиска се
клавиша за
табулация (Space Block Type Soil Let Triange choose Mesh Size Triangle Side Length mm
от лентата
с
инструментите
и се
позиционира един
блоков
етикет
(зелена
точка) за
областта на
почвата.
Щраква се с
десен бутон
върху възела
на блоковия
етикет, така
че възелът да
стане червен,
което е
признак, че
този възел е
избран.
Натиска се
клавиша за
табулация (Space Block Type Soil Let Triange choose Mesh Size Triangle Side Length mm
Conductor Properties Conductors Add Property Circuit properties New Conductor Rod Prescribed Voltage OK
lines Space Segment property Local element size along line
In conductor Rod OK V
Mixed Impedance boundary conditions BC r
Koe c
![]() (20)
(20)
![]() е
специфичната
електрическа
проводимост
на почвата;
е
специфичната
електрическа
проводимост
на почвата;
![]() -
кръговата
честота на
източника;
-
кръговата
честота на
източника;
R
За да се дефинира такова гранично условие се избира Properties Boundry Add Property
Bondary property New Boundry ImpedanceBC От падащото меню BC Type Boundry Condition Type Mixed Mixed BC parameters записва 0.0005 +I e Ok ImpedanceBC
Arc Segment Arc Segment Properties None ImpedanceBC
![]() от
лентата с
инструментите.
Това
действие
генерира
мрежа с триъгълни
крайни
елементи за задачата.
от
лентата с
инструментите.
Това
действие
генерира
мрежа с триъгълни
крайни
елементи за задачата.
FEMM 3768 тетраедални крайни елемента от първи ред(фиг3,б).
FEMM ![]()
lecnet Current flow D
|
|
|
|
|
|
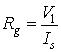 (2
(2
Загубите на енергия в почвата са
![]()
![]()
VE
Стойността
на
съпротивлението,
изчислена по
този начин за
изследвания
заземител е Rg ![]()
![]() на
заземление
могат да
бъдат записани
като се
използва
метода на
електростатичната
аналогия[2], по
известните
формули за
капацитета
на
заземление
могат да
бъдат записани
като се
използва
метода на
електростатичната
аналогия[2], по
известните
формули за
капацитета ![]() на
съответните
тела. Ако
проводящата
среда и
съответно
диелектрика
са еднородни,
то в
уравнението
за
проводимостта
на
съответните
тела. Ако
проводящата
среда и
съответно
диелектрика
са еднородни,
то в
уравнението
за
проводимостта
![]() специфичната
проводимост
специфичната
проводимост ![]() влиза
като
множител и
съответно в
уравнението
за
капацитета
влиза
като
множител и
съответно в
уравнението
за
капацитета ![]() абсолютната
диелектрична
проницаемост
абсолютната
диелектрична
проницаемост
![]() също
влиза като
множител. В
такъв случай
е в сила
следното
съотношение
също
влиза като
множител. В
такъв случай
е в сила
следното
съотношение
![]()
![]()
![]() e
e ![]() ,
, ![]() е
потенциалът
на
зареденото
тяло.
е
потенциалът
на
зареденото
тяло.
![]() е
достатъчно
да се замени
в съответната
формула за
е
достатъчно
да се замени
в съответната
формула за ![]() абсолютните
диелектрични
проницаемости
абсолютните
диелектрични
проницаемости
![]() на
диелектриците
със
специфичните
проводимости
на
диелектриците
със
специфичните
проводимости
![]() на
проводящите
среди.
на
проводящите
среди.
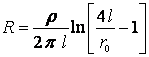 ,
,
![]() е
специфичното
съпротивление
на почвата;
е
специфичното
съпротивление
на почвата;
ro
l
|
Съпротивление
на
заземление, | ||||
|
FEMМ |
Elecnet |
FEMМ |
Elecnet |
|
FEMM 1 V Conductor property
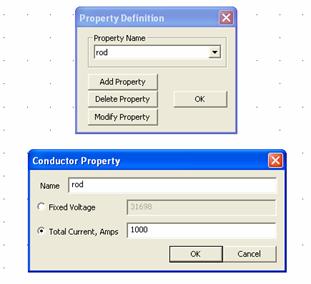
|
|
|
|
Потенциал, V | ||||
|
FEMМ |
Elecnet |
FEMМ |
Elecnet |
|
OX
|
|
|
|
|
|
OY
|
|
|
|
|
|
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3099
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved