Fenomene aeroelastice dinamice

Fenomene aeroelastice dinamice

1.Principalele fenomene aeroelastice dinamice

Fluturarea - reprezinta o instabilitate dinamica caracterizata prin viteza critica si viteza critica a unei miscari oscilatorii.

Buffeting - fenomen cu caracter aleatoriu care apar la nivelul unor componente ale aeronavei ca urmare a curgerii turbulente produse de alte componente.

Raspuns dinamic - reprezinta raspunsul sau miscarea tranzitorie a structurii componentelor aeronavei produse ca urmare a rafalelor aerului, comenzilor bruste, socuri.

Fluturare de panou - este un caz particular de fluturare a unui panou de invelis care separa o cavitate de un curent supersonic.

Fenomenul de fluturare reprezinta cel mai important fenomen aeroelastic dinamic. El apare din interactiunea dintre forte elastice, masice si aerodinamice, din care rezulta o miscare periodica de amplitudine ce poate creste exponential cu timpul. Mecanismul de producere a acestui fenomen este cel al vibratiilor autoexcitate. Din punct de vedere energetic fenomenul de fluturare este neconservativ.

2.Studiu teoretic al fluturarii dinamice

O explicatie fizica a fenomenului de fluturare se poate da considerand urmatorul exemplu. Se va considera o suprafata portanta avand initial incidenta nula. Ea se considera fixata elastic si se presupune ca executa 2 tipuri de miscari, incovoiere si rasucire, aflandu-se in curent de aer cu viteza V

Figura 11

Prin sageti s-a reprezentat forta aerodinamica care actioneaza asupra suprafetei portante. In aceasta situatie se observa ca pe anumite portiumi forta are acelasi sens cu deplasarea, adica lucru mecani este pozitiv, iar pe alte portiuni, forta este in sens opus deplasarii, ceea ce inseamna ca lucru mecanic este negativ. Astfel lucru mecanis pe ansamblu este nul si sistemul nu acumuleaza energie.

Vom considera in continuare profilul avand initial o anumita incidenta:

Figura 12

Se observa ca in aceasta situatie forta, pe tot parcursul perioadei, are mereu acelasi sens cu deplasarea, astfel incat lucru mecanic este doar pozitiv. Aceasta inseamna ca sistemul acumuleaza energie continuu, rezultant autoexcitarea, traducandu-se in fluturare.

Pentru flutter se va alege un model cavsi-stationar pentru calculul fortelor aerodinamice astfel incat putem spune ca local coeficientul de portanta C_z este proportional cu incidenta efectiva.

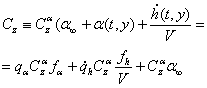
Folosind rezultatele determinate la 2.2. vom avea:

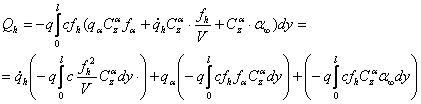
Sistemul:

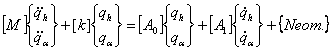
Unde M,K aceleasi

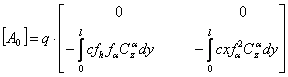
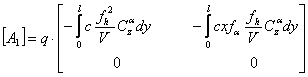
Sistemul omogen:

pentru care se aplica metoda V-g

prescurtat se poate scrie

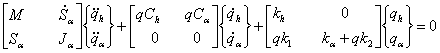
Introducem solutiile:

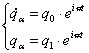
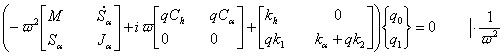
Notam:

unde     - coarda medie aerodinamica

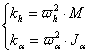
astfel:

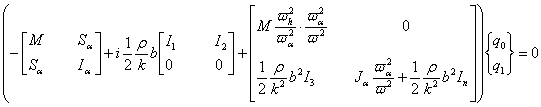
notam:

introducem amortizarea structurala g

Pentru problema cu valori si vectori proprii:

separam a treia matrice

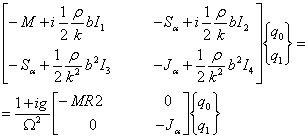
unde:

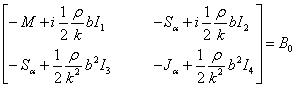
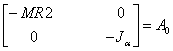
rezulta:

problema de valori si vectori proprii

Rezulta o ecuatie cu coeficienti complecsi in . Dupa determinarea lui se determina g care este raportul dintre partea imaginara si partea reala a solutiei , urmand ca dupa aceea sa se determine pulsatia de fluturare si viteza de fluturare.

Calculul vitezei si a pulsatiei de fluturare ale avionului

Calculul efectiv se face dupa cum urmeaza :

function integ = integ(ss);

integ = (ss(1)+2.*(ss(2)+ss(3)+ss(4)+ss(5)+ss(6)+

ss(7)+ss(8)+ss(9)+ss(10)+ss(11))+ss(12))/2.;

R=0.3; ro=2.560; b=7.45;

i=sqrt(-1);

fh=sin(pi/2.*Y/be); fa=fh;

%Calculul integralei Kh cu formula trapezelor

fh2=(pi/(2.*be))^2*fh;

dd=EIx.*fh2.*fh2; Kh=be/11.*integ(dd);

%Calculul integralei Ka

fa1=-pi/(2.*be)*cos(pi/2.*Y/be);

ss=GJd.*fa1.*fa1; Ka=be/11.*integ(ss);

%Calculul integralei I1

aa=Cz*c.*fh.*fh; I1=be/11.*integ(aa);

%Calculul integralei I2

bb=Cz*c.*fh.*fa.*e; I2=be/11.*integ(bb);

%Calculul matircei I3

ee=Cz*fh.*fa.*c; I3=be/11.*integ(ee);

%Calculul matircei I4

gg=Cz*c.*e.*fa.*fa; I4=be/11.*integ(gg);

%Calculul integralei M

rr=fh.*m.*c; M=be/11.*integ(rr);

%Calculul integralei Ja

cc=1/*c.*c.*c.*m; Ja=be/11.*integ(cc);

%Calculul integralei Sa

hh=1/2.*c.*c.*m; Sa=be/11.*integ(hh);

frec=zeros(2,20000); g=zeros(2,20000); vit=zeros(2,20000);

for k=20000:-1:1; rk=k*0.01;

Bo=[-M+1/2.*ro/rk*b*I1*i -Sa+1/2.*ro/rk*b*I2*i

-Sa+1/2.*ro/rk^2*b^2*I3 -Ja+1/2.*ro/rk^2*b^2*I4];

%Matircea Ao

Ao=[-M*R^2 0

0 -Ja];

%Matricea corespunzatoare valorilor proprii A

A=inv(Ao)*Bo;

vp=eig(A);

g(:,k)=imag(vp)./real(vp);

frec(:,k)=sqrt(1./abs(real(vp)));

vit(:,k)=sqrt(1./abs(real(vp)))/rk;

vpe(:,k)=vp;

im(:,k)=imag(vp);

re(:,k)=real(vp);

while g(:,k) <= 0.002;

ka=rk;

omega=sqrt(1./abs(real(vp))); % Valoarea pulsatiei impartita la omega alfa

g=g+0.01;

end

end

Vitomeg=omega*b/ka;

VF=min(Vitomeg(1),Vitomeg(2)); % Este valoarea vitezei impartita la omega alfa

figure(1);

plot(vit(1,:),frec(1,:),'.k',vit(2,:),frec(2,:),'.k'),

axis([0.0 30.00 -2. 4.]),xlabel('Viteza / omegaalfa * b'),ylabel('Omega / omegaalfa'),grid;

figure(2);

plot(vit(1,:),g(1,:),'.k',vit(2,:),g(2,:),'.k'),

axis([0.0 30.00 -2. 2.]),xlabel('Viteza / omegaalfa * b'),ylabel('g'),grid;

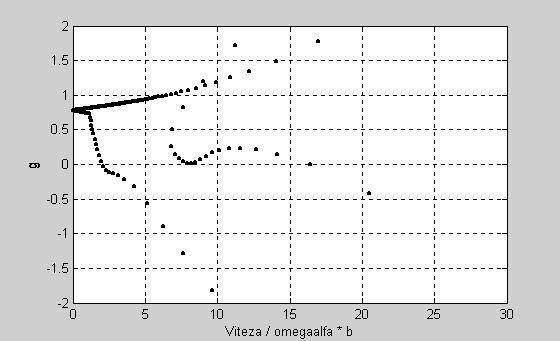
Figura 13

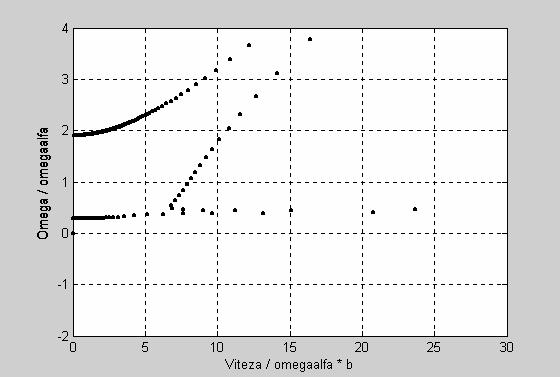
Figura 14

Se obtin pulsatia de fluturare raportata la pulsatia alfa : 0.29896

Si viteza de fluturare raportata la aceeasi pulsatie : 17.31

4.Metoda "Locul radacinilor"

Utilizam sistemul obtinut in cazul metodei V-g :

(1)

(1) se mai scrie:

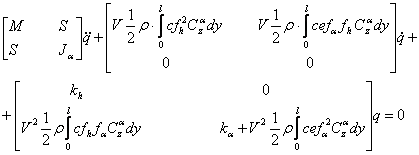
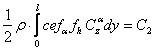
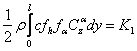
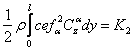
sau:

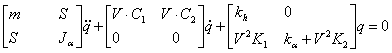
facem notatiile:

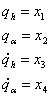
Se va transforma intr-un sistem de 4 ecuatii liniarizate :

matriceal:

cu notatiile facute avem :

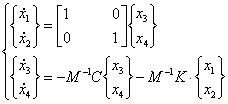
sistemul se mai scrie :

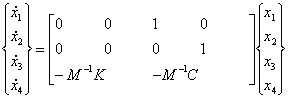
Matricea A depinde de viteza V

Presupunem solutia de forma

unde

Metoda de calcul este urmatoarea:

-oscilatiile armonice se ating atunci cand amplitudinea este 1, adica

-astfel vom da valori vitezei V in matricea

-se calculeaza valorile proprii ale matricii A care se obtin introducand solutia

-se obtin 4 valori proprii complexe

Conditia de oprire a iteratiei este ca viteza de fluturare

Pulsatia de fluturare