SISTEME DE COMUNICATII PENTRU TRANSPORTURI - Analiza Fourier a semnalelor periodice

SISTEME DE COMUNICATII PENTRU TRANSPORTURI

Lucrarea de laborator nr. 1

Analiza Fourier a semnalelor periodice

1. Obiectivul lucrarii

In aceasta lucrare se studiaza analiza semnalelor periodice cu ajutorul seriilor Fourier.

2. Introducere teoretica

2.1. Serii Fourier

Relatia intrare-iesire a unui sistem liniar invariabil in timp (LIT) este data de integrala de convolutie definita prin relatia

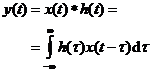
unde prin am notat raspunsul la impuls al sistemului, este semnalul de intrare iar este semnalul de iesire. Daca intrarea este o exponentiala complexa data de

atunci iesirea este data de

Se vede ca iesirea este tot o exponentiala complexa cu aceeasi frecventa ca si intrarea. Amplitudinea iesirii, insa, este amplitudinea intrarii amplificata prin

Se observa ca aceasta marime este o functie de raspunsul la impuls al sistemului LIT, , si de frecventa semnalului de intrare, De aceea, este deosebit de simplu sa se calculeze raspunsul sistemelor LIT la intrari exponentiale. Este, deci, natural in analiza sistemelor liniare sa cautam metode prin care sa dezvoltam semnalele ca sume de exponentiale complexe. Seriile Fourier si transformarile Fourier sunt tehnici pentru dezvoltarea semnalelor in functie de exponentiale complexe.

Sa consideram semnalele periodice cu perioada In dezvoltarea in serie Fourier a unui astfel de semnal, baza pentru dezvoltare este multimea de semnale

Cu aceasta baza, orice semnal periodic cu perioada poate fi exprimat drept o suma infinita

In aceasta dezvoltare, marimile notate cu se numesc coeficientii seriei Fourier a semnalului si sunt date de

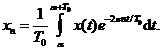
Aceasta relatie se deduce din ortogonalitatea functiilor ce alcatuiesc baza. Marimea α este o constanta arbitrara pe care o alegem astfel incat calculul integralei sa se simplifice. Frecventa se numeste frecventa fundamentala a semnalului periodic, iar frecventa se numeste armonica a n-a. In cele mai multe dintre cazuri, sau este o buna alegere.

Acest tip de serie Fourier se numeste serie Fourier exponentiala si se aplica atat la semnale periodice reale cat si la cele complexe. In general, coeficientii seriei Fourier sunt numere complexe chiar daca este un semnal real.

Daca este un semnal periodic real, avem

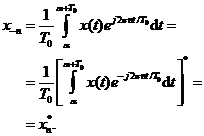
Din aceasta egalitate, este evident ca

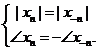
Coeficientii seriei Fourier a unui semnal real au, deci, simetrie Hermite: modulul lor este par iar faza lor este impara. Echivalent, partea lor reala este o functie para de n, iar partea lor imaginara este impara.

O alta forma de serie Fourier, seria Fourier trigonometrica, se poate aplica numai la semnale periodice reale si se obtine definind

Utilizand relatia lui Euler, avem

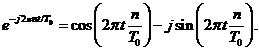
Rezulta ca

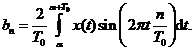
Prin urmare,

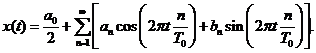
Observam ca, pentru n = 0, avem astfel incat

O a treia forma de serie Fourier se obtine definind

si utilizand relatia trigonometrica

Cu aceasta, putem scrie ecuatia (14) in forma

In general, coeficientii ai seriei Fourier a unui semnal real sunt legati de si prin

Reprezentarea grafica a modulului si a fazei in functie de n sau de se numeste spectrul discret al lui Graficul lui se numeste spectrul de amplitudine, iar graficul lui se numeste spectrul de faza.

Daca este o functie reala si para de timp, adica, daca luand avem ca

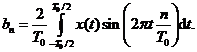
Aceasta integrala este zero fiindca integrandul este o functie impara de t. De aceea, pentru un semnal real si par , toti coeficientii sunt numere reale. In acest caz, seria trigonometrica Fourier consta din toate functiile cosinus. Similar, daca este o functie reala si impara de timp, adica, daca , atunci

este zero si toti coeficientii sunt numere imaginare. In acest caz, seria trigonometrica Fourier consta din toate functiile sinus.

2.2. Raspunsul sistemelor liniare invariabile in timp (LIT) la

semnale periodice

Daca se aplica un semnal periodic la intrarea unui sistem liniar invariabil in timp (LIT), semnalul de iesire este si el periodic cu aceeasi perioada ca semnalul de intrare si de aceea are o dezvoltare in serie Fourier.

Dezvoltam si in serii Fourier:

Relatia dintre coeficientii seriilor Fourier ale lui si se obtine utilizand integrala de convolutie

Fie functia de transfer a sistemului LIT, numita si raspunsul in frecventa al sistemului, dat ca transformata Fourier a raspunsului sau la impuls

Din (23), avem

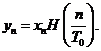
3. Probleme rezolvate cu MATLAB

Problema

Seria Fourier a unui tren de pulsuri rectangulare

Semnalul rectangular notat cu se defineste astfel:

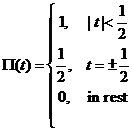
Fie un semnal periodic de perioada definit prin

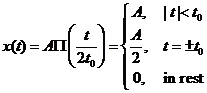
pentru unde

Semnalul este reprezentat grafic in figura 1.

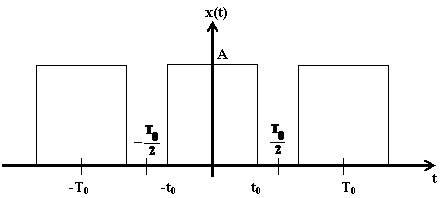
Figura 1. Semnalul din Problema 1.

Presupunand ca A = 1, si

1. Sa se determine coeficientii seriei Fourier a lui in forma exponentiala si in forma trigonometrica.

2. Sa se reprezinte grafic spectrul lui .

Rezolvare

1. Pentru a deduce coeficientii seriei Fourier din dezvoltarea lui , avem

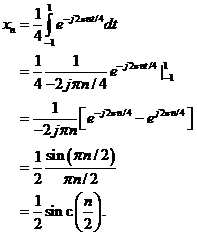
Am definit functia sinus cardinal sinc(x) astfel:

Deoarece este un semnal real si par, toti coeficientii sunt reali, astfel incat

Pentru n = 0, avem ca si Pentru n par, avem ca De aceea

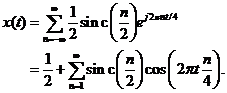
Deoarece este intotdeauna real, in functie de semn, faza este fie zero, fie π. Amplitudinea lui este

Pentru a reprezenta grafic spectrul discret al semnalului, se utilizeaza urmatorul fisier MATLAB:

% Fisier MATLAB pentru Problema 1.

stem(n,x);

Daca semnalul este descris intr-o perioada intre a si b, asa cum se arata in figura 2, iar semnalul din intervalul [a, b] este dat intr-un fisier m, coeficientii seriei Fourier se pot obtine utilizand fisierul m fseries.m dat mai jos.

function xx = fseries(funfcn,a,b,n,tol,p1,p2,p3)

%FSERIES    Returneaza coeficientii seriei Fourier.

XX=FSERIES(FUNFCN,A,B,N,TOL,P1,P2,P3)

funfcn=functia data, intr-un fisier m.

Ea poate depinde de pana la trei parametri p1, p2 si p3.

Functia este data pe o perioada care se intinde de la a la b.

xx=vector de lungime n+1 al coeficientilor seriei Fourier,

xx0,xx1,,xxn.

p1,p2,p3=parametrii lui funfcn.

tol=nivelul erorii.

j=sqrt(-1);

args0=[];

for nn=1:nargin-5

args0=[args0,',p',int2str(nn)];

end

args=[args0,')'];

t=b-a

xx(1)=eval([',num2str(t),') . *quad(funfcn,a,b,tol,[]',args]);

for i=1:n

new_fun = 'exp_fnct' ;

args=[',' , num2str(i), ',', num2str(t), args0, ')'];

xx(i+1)=eval(['1/(',num2str(t),').*quad(new_fun,a,b,tol, [], funfcn',

args]);

end

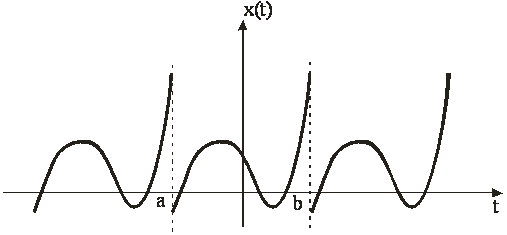
Figura 2. Un semnal periodic.

Problema

Spectrul de amplitudine si spectrul de faza

Sa se determine si sa se reprezinte grafic spectrele discrete de amplitudine si de faza ale semnalului periodic cu o perioada egala cu 8 si definit astfel: pentru

Rezolvare

Semnalul este dat de un fisier m numit lambda.m. Alegem intervalul [a, b] = [-4, 4]. Fisierul fseries.m determina coeficientii seriei Fourier pentru valori pozitive ale lui n. Deoarece este real, avem Reprezentam grafic spectrele de amplitudine si de faza pentru n = 24.

Programul MATLAB pentru determinarea si reprezentarea grafica a spectrelor de amplitudine si de faza este dat mai jos.

% Program MATLAB pentru Problema 2.

echo on

fnct='lambda';

a=-4;

b=4;

n=24;

tol=0.1;

xx=fseries(fnct,a,b,n,tol);

xx1=xx(n+1:-1:2);

xx1=[conj(xx1),xx];

absxx1=abs(xx1);

pause % Apasati orice tasta pentru a vedea o reprezentare grafica a spectrului de amplitudine

n1=[-n:n];

stem(n1,absxx1)

title('Spectrul discret de amplitudine')

phasexx1=angle(xx1);

pause % Apasati orice tasta pentru a vedea o reprezentare grafica a spectrului de faza

stem(n1,phasexx1)

title('Spectrul discret de faza')

Problema

Spectrul de amplitudine si spectrul de faza

Sa se determine si sa se reprezinte grafic spectrul de amplitudine si spectrul de faza ale semnalului periodic cu perioada egala cu 12 care este dat de

in intervalul [-6, 6].

Rezolvare

Semnalul este egal cu functia de densitate a unei variabile aleatoare gaussiene (normale) de varianta unu data in fisierul normal.m. Acest fisier cere doi parametri, m si s, media si abaterea standard a variabilei aleatoare, care in problema sunt 0 si 1, respectiv. De aceea, putem utiliza urmatorul program MATLAB pentru a obtine graficele de amplitudine si de faza.

% Program MATLAB pentru Problema 3

echo on

fnct='normal';

a=-6;

b=6;

n=24;

tol=0.1;

xx=fseries(fnct,a,b,n,tol,0,1);

xx1=xx(n+1:-1:2);

xx1=[conj(xx1),xx];

absxx1=abs(xx1);

pause % Apasati orice tasta pentru a vedea o reprezentare grafica a spectrului de amplitudine

n1=[-n:n];

stem(n1,absxx1)

title('Spectrul discret de amplitudine')

phasexx1=angle(xx1);

pause % Apasati orice tasta pentru a vedea o reprezentare grafica a spectrului de faza

stem(n1,phasexx1)

title('Spectrul discret de faza')

Problema

Filtrarea semnalelor periodice

Un tren de pulsuri triunghiulare cu perioada este definit pe o perioada astfel

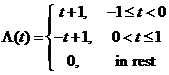
1. Sa se determine coeficientii seriei Fourier a lui .

2. Sa se reprezinte grafic spectrul lui .

3. Presupunand ca acest semnal trece printr-un sistem LIT al carui raspuns la impuls este dat de

sa se reprezinte grafic spectrul discret al iesirii .

Semnalele si sunt reprezentate grafic in figura 3.

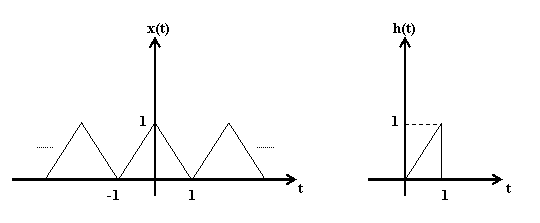
Figura 3. Semnalul de intrare si raspunsul la impuls al sisyemului .

Rezolvare

1. Avem

Indicatie: se utilizeaza integrarea prin parti.

2. Spectrul discret al lui este reprezentat in figura 4.

3. Trebuie mai intai sa deducem , functia de transfer a sistemului. Desi este posibil sa facem aceasta analitic, vom utiliza o metoda numerica. Pentru spectrul discret al semnalului de iesire, avem

Programul MATLAB este urmatorul:

% Program MATLAB pentru Problema 4.

echo on

n=[-20:1:20];

% coeficientii seriei Fourier a vectorului

x=.5*(sinc(n/2)).^2;

% interval de esantionare

ts=1/40;

% vector timp

t=[-.5:ts:1.5];

% raspuns la impuls

fs=1/ts;

h=[zeros(1,20),t(21:61),zeros(1,20)];

% functia de transfer

H=fft(h)/fs;

% rezolutia de frecventa

df=fs/80;

f=[0:df:fs]-fs/2;

% rearanjeaza H

H1=fftshift(H);

y=x.*H1(21:61);

% urmeaza comenzile de reprezentare grafica.

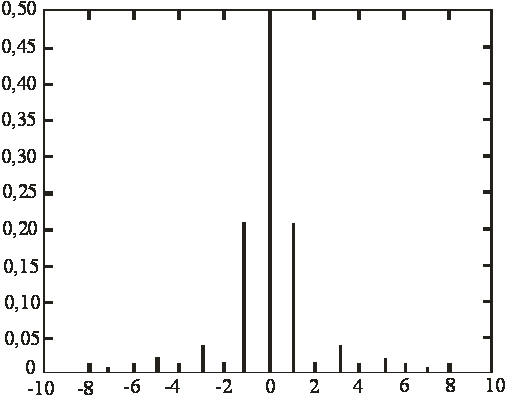
Figura 4. Spectrul discret al semnalului .