| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
CIRCUITE DINAMICE - CIRCUITE DE CURENT ALTERNATIV MONOFAZAT
1. Introducere.
Comportarea circuitelor rezistive,
formate din surse independente si rezistoare multipolare este descrisa, asa cum
s-a aratat in Capitolul 2, de un sistem de ecuatii algebrice. In acest capitol
se va introduce o clasa noua de elemente de circuit a caror comportare este
descrisa de ecuatii diferentiale. Aceste elemente de circuit se numesc elemente
dinamice. Cele mai simple elemente din aceasta clasa sunt doua elemente
dipolare: condensatorul liniar si bobina liniara. Ecuatia de functionare a
condensatorului liniar este ![]() unde u(t) este tensiunea la bornele
condensatorului, i(t) este curentul
prin condensator si C este o
constanta numita capacitatea condensatorului. Ecuatia de functionare a bobinei
liniare este
unde u(t) este tensiunea la bornele
condensatorului, i(t) este curentul
prin condensator si C este o
constanta numita capacitatea condensatorului. Ecuatia de functionare a bobinei
liniare este ![]() unde L este o
unde L este o
Un circuit care contine cel putin un element dinamic se numeste circuit dinamic. Elementele dinamice ideale sunt, spre deosebire de rezistoare, elemente fara pierderi adica ele nu disipa energia ci o acumuleaza. Energia acumulata la un moment dat de un astfel de element poate fi ulterior cedata circuitului in care este conectat elementul respectiv.
Un circuit functioneaza in regim sinusoidal daca toate tensiunile si toti curentii sunt marimi sinusoidale de aceeasi pulsatie. Un astfel de circuit se numeste circuit de curent alternativ (c.a.).
Fie un circuit liniar cu rezistoare cu rezistentele pozitive, bobine cu inductivitatile pozitive, condensatoare cu capacitatile pozitive si in care toate sursele independente sunt sinusoidale de aceeasi pulsatie w. Se poate arata ca un astfel de circuit functioneaza in regim sinusoidal atunci cand timpul care trece de la cuplarea surselor tinde catre infinit. Spunem ca regimul permanent (care se obtine pentru pentru t¥) al acestui circuit este sinusoidal. In Capitolul 5 se arata ca daca intr-un astfel de circuit avem un singur element neliniar, regimul permanent, daca exista, este unul nesinusoidal (deformant) in care raspunsul contine componente de pulsatiile 2w, 3w, Regimul sinusoidal este deci regimul permanent al unei clase de circuite liniare.
Importanta studiului acestui regim este legata de faptul ca energia electrica se produce cu generatoare sinusoidale si se distribuie eficient prin circuite de curent alternativ; in plus foarte multe circuite electronice functioneaza in acest regim.
2. Elementele dinamice de circuit
2.1. Condensatorul ideal.
Din teoria campului electromagnetic
se stie ca relatia intre sarcina q a unui corp si curentul absorbit de acesta
este i=dq/dt. Ca urmare un element dipolar de circuit poate fi caracterizat, pe
langa perechea , si de sarcina
electrica q(t) definita de relatia. 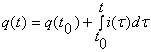 in care
in care 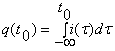 este sarcina in momentul t0.
este sarcina in momentul t0.
Condensatorul ideal este un element dipolar de circuit pentru care multimea perechilor admisibile poate fi reprezentata in planul q-u printr-o curba de ecuatie f(q,u)=0. Aceasta curba este caracteristica q-u a condensatorului si ecuatia f(q,u)=0 este ecuatia sa constitutiva. Daca f(q,u)=0 este aceeasi pentru orice moment de timp, condensatorul este invariant in timp.
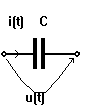
Marimea 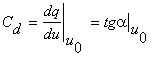 se numeste capacitatea dinamica a condensatorului
la tensiunea u0. Daca
caracteristica condensatorului este o dreapta care trece prin origine
condensatorul este liniar iar marimea
Cd este
se numeste capacitatea dinamica a condensatorului
la tensiunea u0. Daca
caracteristica condensatorului este o dreapta care trece prin origine
condensatorul este liniar iar marimea
Cd este ![]() .
.
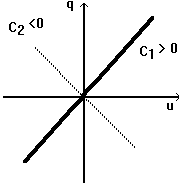
Unitatea de
masura a capacitatii este faradul ( ![]() ), in practica
folosindu-se submultiplii sai microfaradul (1mF = 10-6 F) ,
nanofaradul (1nF = 10-9 F) si picofaradul (1pF = 10-12F).
), in practica
folosindu-se submultiplii sai microfaradul (1mF = 10-6 F) ,
nanofaradul (1nF = 10-9 F) si picofaradul (1pF = 10-12F).
Daca caracteristica condensatorului
nu este o dreapta care trece prin origine atunci condensatorul este neliniar. Un condensator este controlat
in tensiune daca ecuatia sa constitutiva poate fi scrisa ca o functie ![]() si este controlat in
sarcina daca exista functia
si este controlat in
sarcina daca exista functia ![]() . Comportarea acestui element de circuit este descrisa de
ecuatia constitutiva f(q,u)=0 la care
se adauga ecutia
. Comportarea acestui element de circuit este descrisa de
ecuatia constitutiva f(q,u)=0 la care
se adauga ecutia ![]() . In unele cazuri se poate explicita dependenta dintre curent
si derivata tensiunii in raport cu timpul; aceasta dependenta este ecuatia de functionare a
condensatorului. De exemplu:
. In unele cazuri se poate explicita dependenta dintre curent
si derivata tensiunii in raport cu timpul; aceasta dependenta este ecuatia de functionare a
condensatorului. De exemplu:
-pentru un condensator liniar
invariant in timp : ![]() si
si ![]()
-pentru un condensator neliniar
controlat in tensiune :![]()
Condensatorul ideal modeleaza un efect capacitiv.
2.2. Bobina ideala
Din teoria campului electromagnetic
se stie ca relatia intre fluxul magnetic j(t) al unei bobine si tensiunea u(t) la bornele acesteia este
u(t)=dj(t)/dt. Ca
urmare un element dipolar de circuit poate fi caracterizat, pe langa perechea
, si de fluxul magnetic j(t) definit de relatia. 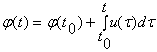 in care
in care 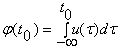 este fluxul magnetic
in momentul t0.
este fluxul magnetic
in momentul t0.
O bobina este un element dipolar de circuit pentru care multimea perechilor admisibile poate fi reprezentata in planul j-i printr-o curba de ecuatie f(j,i)=0. Aceasta curba este caracte-
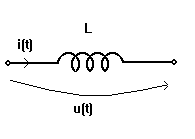
ristica j-i a bobinei si ecuatia f(j,i)=0 este ecuatia sa constitutiva. Daca f(j,i)=0 este aceeasi pentru orice moment de timp, bobina este invarianta in timp.
Marimea 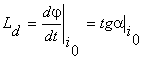 se numeste inductivitatea dinamica a bobinei la
curentul i0. Daca
caracteristica bobinei este o dreapta care trece prin origine bobina este
liniara si marimea Ld devine
se numeste inductivitatea dinamica a bobinei la
curentul i0. Daca
caracteristica bobinei este o dreapta care trece prin origine bobina este
liniara si marimea Ld devine ![]() . Unitatea de masura a inductivitatii este 1 henry (1H= 1Wb/1A); in practica se folosesc
submultiplii milihenry (mH) si microhenry (mH).
. Unitatea de masura a inductivitatii este 1 henry (1H= 1Wb/1A); in practica se folosesc
submultiplii milihenry (mH) si microhenry (mH).
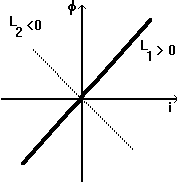
Daca caracteristica bobinei nu este
o dreapta care trece prin origine atunci bobina este neliniara. O bobina este controlata in curent daca ecuatia sa
constitutiva poate fi scrisa in forma ![]() si este controlata in
flux daca exista functia
si este controlata in
flux daca exista functia ![]() . Comportarea acestui element de circuit este descrisa de
ecuatia constitutiva f(
. Comportarea acestui element de circuit este descrisa de
ecuatia constitutiva f(![]() ,i)=0 la care se
adauga ecutia
,i)=0 la care se
adauga ecutia ![]() . In unele cazuri se poate explicita dependenta dintre
tensiune si derivata curentului in raport cu timpul; aceasta dependenta este ecuatia de functionare a bobinei. De
exemplu:
. In unele cazuri se poate explicita dependenta dintre
tensiune si derivata curentului in raport cu timpul; aceasta dependenta este ecuatia de functionare a bobinei. De
exemplu:
-pentru o bobina liniara invarianta
in timp : ![]() si
si ![]()
-pentru o bobina neliniara
controlata in curent :![]()
Bobina ideala modeleaza un efect inductiv.
2. Proprietati ale condensatoarelor si bobinelor.
2.1. Memoria.
La un rezistor dipolar controlat in tensiune curentul i(t) depinde numai de tensiunea din acelasi moment (i(t) = f1 (u(t)) ) iar la un rezistor controlat in curent u(t)=f2 (i(t)) ceeace insemna ca rezistoarele nu au memorie.
La orice condensator sarcina q(t) depinde de valorile curentului intr-un interval de timp [t0,.t] si
de sarcina q(t0) [q(t)=q(t0)+![]() ]. Similar, fluxul magnetic prin bobina j (t) depinde de j(t0 ) si de valorile tensiunii
bobinei in intervalul [t0,.t] [j(t)= j (t0 )
+
]. Similar, fluxul magnetic prin bobina j (t) depinde de j(t0 ) si de valorile tensiunii
bobinei in intervalul [t0,.t] [j(t)= j (t0 )
+ ![]() ]. Aceasta inseamna ca
bobina si condensatorul sunt elemente de
circuit cu memorie, spre deosebire de rezistor.
]. Aceasta inseamna ca
bobina si condensatorul sunt elemente de
circuit cu memorie, spre deosebire de rezistor.
2.2. Continuitatea lui uC si iL
Fie condensatorul din figura de mai
jos prin care trece curentul iS(t) care are discontinuitati finite.
Rezulta ca daca uC (0)=0 atunci uC (t)=![]() si uC (t) este o functie continua. Pe baza
proprietatii de continuitate a integralei unei functii cu discontinuitati
finite rezulta:
si uC (t) este o functie continua. Pe baza
proprietatii de continuitate a integralei unei functii cu discontinuitati
finite rezulta:
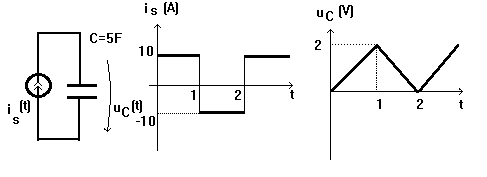
a)daca curentul iC(t) printr-un condensator liniar invariant in timp este marginit si are un numar finit de discontinuitati in intervalul [t0, tp] atunci tensiunea condensatorului uC(t) este continua in acest interval;
b)daca tensiunea uL(t) pe o bobina liniara invarianta in timp este marginita si are un numar finit de discontinuitati in intervalul [t0, tp] atunci curentul prin bobina iL(t) este continuu in acest interval.
Daca iC(t), respectiv uL(t), nu sunt marginite atunci uC(t), respectiv iL(t) nu sunt marimi continue. De exemplu daca condensatorul din figura de mai jos este alimentat cu tensiunea e(t) (e(t) este o functie continua de timp), atunci iC(t) va avea discontinuitati finite. Daca D0 atunci e(t) devine
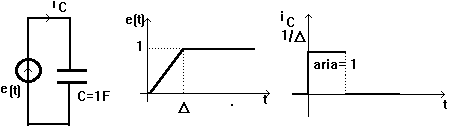
functia treapta unitate care are o discontinuitate in t=0 si iC(t) nu mai este marginit. Cand D0
dreptunghiul isi mentine aria unitara latimea sa tinzand catre zero si inaltimea sa spre infinit. Semnalul obtinut astfel se numeste impuls unitar sau impuls Dirac si se noteaza d(t).
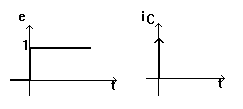
Functia d(t) are o singularitate in
t=0 si este nula pentru t¹0. Se poate
arata usor ca ![]() pentru orice e1 si e2 strict
pozitivi.
pentru orice e1 si e2 strict
pozitivi.
2. Caracterul nedisipativ (fara pierderi)
Energia pe care o primeste un
rezistor liniar cu R>0 in intervalul de timp [t1, t2 ]
este: 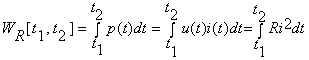 . Evident W[t1, t2] ³0
indiferent de semnul lui i(t). Daca rezistorul este neliniar si pasiv [u(t)i(t)³0]
rezultatul este acelasi: Rezistorul pasiv primeste energie din circuitul in
care este conectat si aceasta energie se transforma in mod ireversibil in
caldura (se disipa). Spunem ca rezistorul
pasiv este un element de circuit disipativ (cu pierderi).
. Evident W[t1, t2] ³0
indiferent de semnul lui i(t). Daca rezistorul este neliniar si pasiv [u(t)i(t)³0]
rezultatul este acelasi: Rezistorul pasiv primeste energie din circuitul in
care este conectat si aceasta energie se transforma in mod ireversibil in
caldura (se disipa). Spunem ca rezistorul
pasiv este un element de circuit disipativ (cu pierderi).
Energia absorbita de un condensator liniar in intervalul de timp [t1, t2 ]este
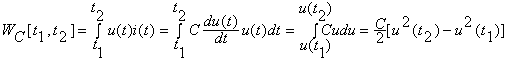
Daca u(t) este periodica de perioada T si t2=t1+T, atunci WC[t1, t2]=0 si energia medie absorbita de condensator intr-o perioada este nula. Aceasta inseamna ca puterea absorbita este pozitiva numai pe anumite subintervale din perioada T, in celelalte subintervale puterea absorbita fiind negativa. Deci condensatorul nu disipa energia ci o acumuleaza si apoi o reda circuitului in care este conectat. Un astfel de element de circuit este nedisipativ (fara pierderi).
Pentru un condensator controlat in sarcina [u=u(q)] rezultatul este similar
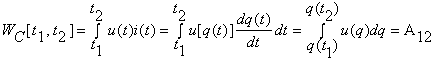 , unde A12 este aria din figura.
, unde A12 este aria din figura.
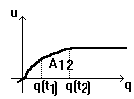
Daca q(t2) =q(t1 + T ) atunci A12 = 0 si WC [t1, t2] = 0.
Similar se poate arata ca o bobina liniara si o bobina neliniara controlata in flux sunt nedisipative. Pentru bobina liniara
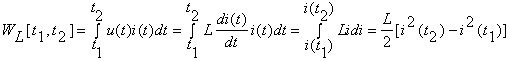
si pentru bobina neliniara controlata in flux cu caracteristica i=i(f)
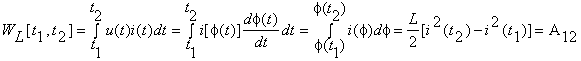
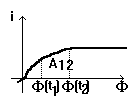
Din aceaste relatii rezulta ca in regim periodic (u(t) si i(t) sunt functii periodice de perioada T) la un element de circuit fara pierderi tensiunea si curentul trec prin valoarea zero la momente de timp diferite. Altfel produsul u(t)i(t) ar fi tot timpul pozitiv sau negativ si W[t1, t2] ar fi nenula pe o perioada. De exemplu, in regim sinusoidal tensiunea unui condensator liniar este u(t)=U sinwt si curentul este i(t)=Cw coswt=Cw sin(wt +p/2) deci u(t) si i(t) trec prin zero la momente de timp distantate cu Dt = p/2w.
Fie un condensator liniar cu capacitatea C>0 care in momentul t1 este conectat la un circuit .
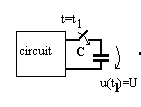
Stiind ca
u(t1)=U, energia absorbita de condensator este WC=[t1,t2]=![]() . Daca
. Daca
![]() , atunci WC [t1, t2 ] < 0 si
condensatorul cedeaza energie circuitului la care este conectat.
, atunci WC [t1, t2 ] < 0 si
condensatorul cedeaza energie circuitului la care este conectat.
Daca u(t2) = 0
condensatorul va ceda valoarea maxima a energiei WCmax [t1, t2 ]=![]() . Deoarece aceasta este valoarea maxima a energiei ce se
poate extrage din condensator este normal sa spunem ca energia acumulata intr-un condensator liniar de capacitate C incarcat
la tensiunea U este EC =
. Deoarece aceasta este valoarea maxima a energiei ce se
poate extrage din condensator este normal sa spunem ca energia acumulata intr-un condensator liniar de capacitate C incarcat
la tensiunea U este EC = ![]() . Similar se poate arata ca energia acumulata intr-o bobina
liniara de inductivitate L prin care trece curentul I este
. Similar se poate arata ca energia acumulata intr-o bobina
liniara de inductivitate L prin care trece curentul I este ![]() .
.
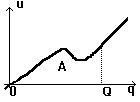
Pentru un
condensator neliniar controlat in sarcina a carui caracteristica u=u(q) trece
prin origine energia acumulata este ![]()
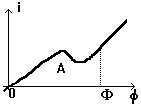
Pentru o
bobina neliniara controlata in flux a carei caracteristica i = i(F) trece prin origine energia
acumulata este ![]()
2.4 Bobinele cuplate
Bobinele cuplate se utilizeaza in circuitele de comunicatii si in echipamentele de masura. Transformatoarele electrice construite cu bobine cuplate au o importanta deosebita in transmiterea energiei electrice intre generatoare si utilizatori. Motoarele si generatoarele electrice se modeleaza prin bobine cuplate cu parametri variabili in timp.
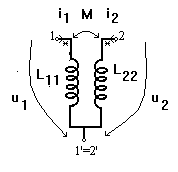
. Doua bobine cuplate magnetic se reprezinta astfel
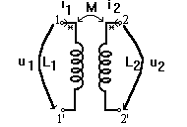
Un model liniar al acestui dispozitiv este dat de un sistem de ecuatii liniare care leaga curentii i1, i2 si fluxurile f1, f2 prin bobinele 1 si 2. Acest sistem reprezinta ecuatia constitutiva a bobinelor liniare cuplate:
f1 = L11 i1 Mi2
f2 = L22i2 Mi1.
unde L11 si L22 sunt inductivitatile proprii ale celor doua infasurari si M este inductivitatea mutuala dintre infasurari. Termenii L11 i1 si L22i2 reprezinta fluxurile proprii ale bobinelor 1 si 2 iar termenii Mi2 si Mi1 reprezinta fluxurile mutuale. In teoria campului electromagnetic se arata ca fluxul propriu si fluxul mutual sau se aduna in ambele bobine, sau se scad in ambele bobine. Ca urmare semnele atasate
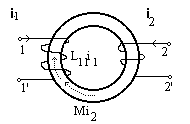
lui M sunt sau amandoua + sau amandoua -. De exemplu pentru bobina 1 din figura, cu sensurile date
pentru i1 si i2 fluxul propriu L11 i1 si fluxul mutual M i2 sunt orientate in acelasi sens si deci M se
considera cu semnul +. Daca i2 are sensul invers celui din figura, atunci fluxul mutual este orientat invers fata de cel propriu si M se considera cu semnul -.
Pentru a preciza semnul lui M se foloseste reprezentarea bobinelor cu borne polarizate: daca cei doi curenti i1 si i2 "ataca" la fel bornele polarizate (ambii intra sau ambii ies din aceste borne), atunci in ecuatii se considera +M, iar daca i1 si i2 "ataca" in mod diferit aceste borne (un curent intra prin borna polarizata si celalalt curent iese prin borna polarizata) atunci in ecuatii se considera -M.
Ecuatia constitutiva a bobinelor cuplate se scrie matriceal [F] = [L].[I]
unde ![]() este matricea inductivitatilor.
este matricea inductivitatilor.
Tensiunile u1 si u2 sunt date
de ![]() si
si ![]() aceste relatii
reprezentand ecuatia de functionare a
bobinelor cuplate. Utilizand ecuatia constitutiva a bobinelor liniare
rezulta:
aceste relatii
reprezentand ecuatia de functionare a
bobinelor cuplate. Utilizand ecuatia constitutiva a bobinelor liniare
rezulta:
![]()
![]()
sau,
matriceal, ![]()
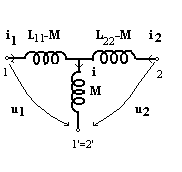
Daca nodurile 1' si 2' sunt legate intre ele atunci se poate obtine un diport echivalent cu trei bobine necuplate. Deoarece i=i1+i2, calculand u1(t) in diportul echivalent rezulta:
![]() . Similar rezulta
. Similar rezulta ![]() .
.
Similar cu elementele dipolare, pentru a calcula energia acumulata se considera conditii initiale nule (i1(0)=0 si i2(0)=0, respectiv f1(0)=0 si f2(0)=0). Se calculeaza energia absorbita de bobine intr-un interval de timp T:
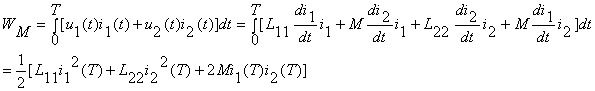
Energia acumulata in bobine la momentul T poate fi calculata ca energia cedata de bobine in transformarea de la starea initiala la starea finala i1(T)=I1, i2(T)=I2.
![]()
Din considerente fizice energia magnetica acumulata WM(I1, I2) este pozitiva pentru orice I1, I2¹0. Rezulta ca L este pozitiv definita, deci minorii principali ai matricei L sunt pozitivi adica L11³0, L11L22 -M2 ³0.
Inductivitatea mutuala se poate
defini in functie de coeficientul de cuplaj ![]() . Din L11L22 ³ M2 rezulta ca
. Din L11L22 ³ M2 rezulta ca ![]() <1. Valoarea k=0 corespunde bobinelor necuplate, iar
valoarea k=1 corespunde cuplajului perfect.
<1. Valoarea k=0 corespunde bobinelor necuplate, iar
valoarea k=1 corespunde cuplajului perfect.
In cazul mai multor bobine cuplate se obtin ecuatii similare. De exemplu trei bobine liniare cuplate au ecuatia de functionare
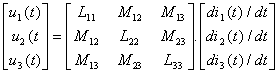
In teoria campului electromagnetic se demonstreaza relatia Mjk=Mkj (proprietatea de simetrie a matricei inductivitatilor).
Ecuatia de functionare a unui sistem
de bobine neliniare cuplate se obtine din relatiile ![]() si ecuatiile constitutive. De exemplu pentru doua bobine
neliniare controlate in curent cu ecuatiile
constitutive
si ecuatiile constitutive. De exemplu pentru doua bobine
neliniare controlate in curent cu ecuatiile
constitutive ![]() rezulta:
rezulta: 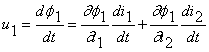 si
si
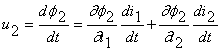 .
.
Reprezentarea in complex a marimilor sinusoidale
O marime sinusoidala este o functie de timp de forma: y(t) =![]() Y sin(t +)
Y sin(t +)
unde: Y
este valoarea efectiva, ![]() Y este valoarea maxima, este pulsatia si =2f unde f = 1/T este
frecventa si T este perioada,iar este faza initiala.
Y este valoarea maxima, este pulsatia si =2f unde f = 1/T este
frecventa si T este perioada,iar este faza initiala.
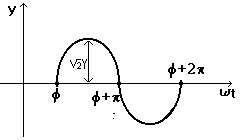
Reprezentarea in complex a marimii sinusoidale y(t) = ![]() Y sin(t + j) este numarul complex
Y sin(t + j) este numarul complex ![]() unde Y este modulul
numarului complex, j este
argumentul numarului complex, iar
unde Y este modulul
numarului complex, j este
argumentul numarului complex, iar ![]() . Evident Y=Ycosj + jYsinj, unde Ycosj este partea reala a lui Y
si Ysinj este
partea sa
. Evident Y=Ycosj + jYsinj, unde Ycosj este partea reala a lui Y
si Ysinj este
partea sa
imaginara.
Reprezentarea grafica a lui Y in planul complex se numeste fazor.
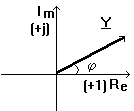
Proprietati:
a) liniaritatea: ay1 (t) + by2 (t) Û aY1+ bY 2 cu a,bIR
Demonstratie: Este evident ca ay1 (t) aY1. Ramane de aratat ca y1 + y2 Y1 + Y2
Fie ![]() si
si ![]() . Atunci
. Atunci
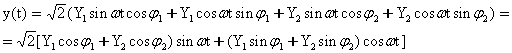
Notam:
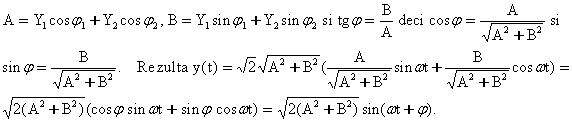
Reprezentarea in complex a lui y(t) va fi:
![]()
b)
derivarea marimii sinusoidale in raport cu timpul: ![]() Û j Y
Û j Y
![]() Y
Y![]() cos (t + ) = Y
cos (t + ) = Y![]() sin (t + +
sin (t + + ![]() ) Û Y ej( +
) Û Y ej( + ![]() ) = j Y
) = j Y
Exemple:a) Fie marimea sinusoidala y(t) = 120![]() sin (wt + p/2). Numarul complex
corespunzator este Y = Yejj cu Y = 120
si j = p/2, respectiv Y =
120ejp/2 = 120 (
cos p/2 +jsin p/2) = 120j. Daca y(t) = 100
sin (wt + p/4), atunci Y =
sin (wt + p/2). Numarul complex
corespunzator este Y = Yejj cu Y = 120
si j = p/2, respectiv Y =
120ejp/2 = 120 (
cos p/2 +jsin p/2) = 120j. Daca y(t) = 100
sin (wt + p/4), atunci Y = ![]() ejp/4 =
ejp/4 =![]() ( cosp/4 +jsinp/4 ) Û 50 ( 1+j
).
( cosp/4 +jsinp/4 ) Û 50 ( 1+j
).
b) Fie numarul complex Y =
3+4j. Marimea sinusoidala corespunzatoare este y(t) = Y![]() sin(wt + j) cu Y =
sin(wt + j) cu Y =![]() = 5 si j = arctg
4/3 = 580 si deci y(t) = 5
= 5 si j = arctg
4/3 = 580 si deci y(t) = 5![]() sin (wt +580
)
sin (wt +580
)
4. Caracterizarea in complex a elementelor de circuit
4.1. Elementele dipolare
Se considera un element dipolar de circuit (EDC) avand tensiunea la borne u(t)=
U![]() sin(wt+ju) si
curentul i(t)=I
sin(wt+ju) si
curentul i(t)=I![]() sin (wt+ji) respectiv
in complex U=Uejju si I = Iejji unde j = ju - ji este defazajul intre tensiune si
curent.
sin (wt+ji) respectiv
in complex U=Uejju si I = Iejji unde j = ju - ji este defazajul intre tensiune si
curent.
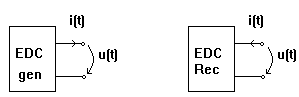
Considerand u(t) si i(t) asociati
dupa regula de la receptoare (ca si marimile complexe corespunzatoare U
si I) se defineste impedanta
complexa a EDC ca raportul dintre tensiunea U si curentul I: Z
= ![]() =
= 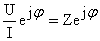 unde raportul Z =
unde raportul Z = ![]() este impedanta EDC. Z si Z se masoara in W. Se noteaza Z= R +
jX unde Re=R este rezistenta de
curent alternativ si Im=X este reactanta si deci Z=R + jX =
este impedanta EDC. Z si Z se masoara in W. Se noteaza Z= R +
jX unde Re=R este rezistenta de
curent alternativ si Im=X este reactanta si deci Z=R + jX =![]()
Se defineste admitanta complexa Y a unui element de circuit ca raportul
dintre curentul I si tensiunea U: ![]() unde Y este admitanta
EDC, G=Re este conductanta EDC si
B=Im este susceptanta EDC. Y
si Y se masoara in Siemens (W- 1 ).
unde Y este admitanta
EDC, G=Re este conductanta EDC si
B=Im este susceptanta EDC. Y
si Y se masoara in Siemens (W- 1 ).
In continuare sunt prezentate elementele dipolare de circuit in c.a. si schemele lor echivalente in complex. Pentru surse u(t) si i(t) se considera asociate dupa regula de la generatoare. Pentru celelalte elemente de circuit u(t) si i(t) se considera asociate dupa regula de la receptoare.
Sursa ideala de tensiune are
tensiunea electromotoare sinusoidala e(t) =![]() E sin(wt + a). e(t)ÛE=Eeja. In figura
sunt desenate sursa si schema ei echivalenta in complex.
E sin(wt + a). e(t)ÛE=Eeja. In figura
sunt desenate sursa si schema ei echivalenta in complex.
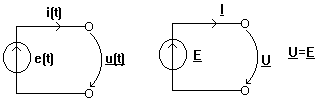
Sursa ideala de curent are curentul electromotor is(t) =![]() Is sin(wt + ) cu reprezentarea in
Is sin(wt + ) cu reprezentarea in
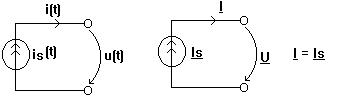
complex Is= Eej si schema echivalenta din figura.
Rezistorul ideal Daca u(t) =![]() U sinwt atunci
i(t) =
U sinwt atunci
i(t) = ![]() =
= ![]()
![]() sinwt, U=RI si
deci ZR =R si
sinwt, U=RI si
deci ZR =R si
rezistorul are schema echivalenta in complex din figura. In schemele echivalente in complex impedantele complexe se simbolizeaza ca niste rezistoare.
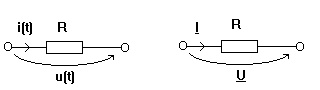
Defazajul intre tensiune si curent este j = ju - ji = 0 si reprezentarea fazoriala a lui U si I este:
![]()
Bobina ideala Daca i(t) = ![]() Isinwt atunci
din ecuatia de functionare u(t) = L
Isinwt atunci
din ecuatia de functionare u(t) = L![]() =
= ![]() ILwsin(wt+p/2)
ILwsin(wt+p/2)![]() rezulta in complex U= jwLI si deci ZL
= jwL = jXL
,unde XL=wL este
reactanta inductiva a bobinei.
rezulta in complex U= jwLI si deci ZL
= jwL = jXL
,unde XL=wL este
reactanta inductiva a bobinei.
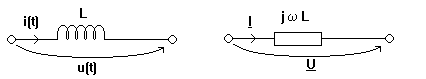
Deoarece j= ju - ji= p / 2 reprezentarea fazoriala a lui U si I este
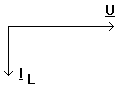
deci spunem ca bobina ideala defazeaza cu p / 2 tensiunea inaintea curentului (sau curentul in urma tensiunii).
Condensatorul ideal Daca u(t) = ![]() Usinwt atunci
din ecuatia de functionare i(t) = C
Usinwt atunci
din ecuatia de functionare i(t) = C![]() =
= ![]() UCwsin(wt+p/2)
UCwsin(wt+p/2)![]() rezulta I= jwC U sau U =
rezulta I= jwC U sau U = ![]() I si deci ZC=
-j
I si deci ZC=
-j ![]() = jXC,
unde XC= -
= jXC,
unde XC= -![]() este reactanta capacitiva a condensatorului.
este reactanta capacitiva a condensatorului.
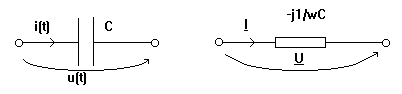
Deoarece j = ju-ji=-p/2 reprezentarea fazoriala a lui U si I este

deci condensatorul ideal defazeaza cu p / 2 tensiunea in urma curentului (sau curentul inaintea tensiunii).
Observatii
i)
reprezentarea in complex a unei marimi sinusoidale (tensiune sau curent) are
numai 2 parametri (Y, ![]() ,). Doi dintre cei trei parametric (Y,
,). Doi dintre cei trei parametric (Y, ![]() ,
, ![]() ) ai marimii sinusoidale
corespunzatoare. Parametrul
) ai marimii sinusoidale
corespunzatoare. Parametrul ![]() intervine in
expresiile impedantelor complexe
intervine in
expresiile impedantelor complexe
ii) Sistemul de ecuatii diferential algebric care caracterizeaza un circuit liniar dinamic in regim sinusoidal corespunde unui sistem de ecuatii algebrice in complex; aceasta proprietate constituie principalul avantaj al utilizarii reprezentarii in complex a marimilor sinusoidale deoarece manipularea (inclusive rezolvarea) unor ecuatii algebrice este considerabil mai simpla decat a unor ecuatii diferentiale.
4.2. Elementele multipolare
Un circuit de curent alternativ poate contine orice element liniar de circuit. Dintre elementele rezistive multipolare liniare reamintim sursele comandate liniar (prezentate in paragraful 2.1.2) si circuitul echivalent liniar pentru semnale mici al tranzistorului (prezentat in paragraful 2.5.3). Prin analogie cu rezistorul liniar, este evident ca o sursa comandata liniar are ca schema echivalenta in complex tot o sursa comandata liniar; de exemplu o SCCC cu ecuatia de functionare is(t)= i1(t) are ca schema echivalenta in complex o SCCC cu ecuatia de functionare Is= I1. In consecinta circuitul echivalent liniar pentru semnale mici al tranzistorului are schema echivalenta in complex:
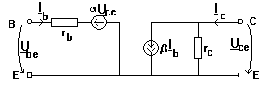
Dintre elementele dinamice multipolare liniare cel mai des utilizat este perechea de bobine cuplate magnetic. Ecuatiile de functionare a doua bobine liniare cuplate magnetic sunt:
u1(t) = L1 ![]() M
M ![]() , u2(t) = L2
, u2(t) = L2 ![]() M
M ![]()
In complex aceste ecuatii devin: U1=jwL1I1jwMI2 , U2=jwL2I2jwMI1
Schema echivalenta in complex contine doua impedante inductive cuplate intre ele. La bornele unei astfel de impedante avem o cadere de tensiune proprie si o cadere de tensiune mutuala. De exemplu
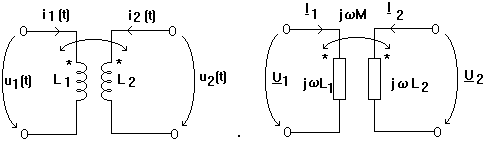
U1 este formata din caderea de tensiune proprie jwL1I1 si caderea de tensiune mutuala jwMI2; semnul caderii de tensiune mutuale este + daca curentii I1 si I2 ataca la fel bornele polarizate (ambii intra sau ambii ies din aceste borne) sau - daca curentii I1 si I2 ataca diferit bornele polarizate (unul intra si celalalt iese din borna polarizata) (vezi paragraful 2.4.). Deci de fiecare data cand se scriu ecuatiile circuitului trebuie determinate semnele caderilor de tensiune mutuala.
Aceleasi ecuatii in complex corespund si urmatorului circuit echivalent cu surse de tensiune comandate in curent:
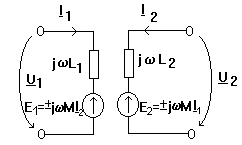
Intr-adevar calculand U1 ca suma intre caderea de tensiune la bornele impedantei jwL1 si tensiunea la bornele sursei comandate rezulta U1=jwL1I1jwMI2. O verificare similara se poate face si pentru U2. In expresiile E1 si E2 se considera semnul + daca curentii I1 si I2 ataca la fel bornele polarizate si semnul - daca le ataca diferit. Se prefera utilizarea acestui circuit in locul schemei cu bornele polarizate. Aceasta deoarece semnele E1 si E2 se stabilesc atunci cand se construieste circuitul echivalent, aceasta operatiune fiind facuta separat de cele implicate de scrierea ecuatiilor. Se diminueaza astfel posibilitatea de a gresi, fata de utilizarea schemei cu borne polarizate in care semnele caderilor de tensiune mutuale se stabilesc in timpul scrierii ecuatiei.
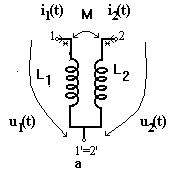
Daca cele doua bobine cuplate au un nod comun exista un circuit echivalent mai simplu fara surse comandate. Ecuatiile de functionare ale celor doua bobine cuplate sunt: U1=jwL1I1 + jwMI2 si U2=jwL2I2 + jwMI1. Daca in prima ecuatie se aduna si se scade jwMI1 si in a doua ecuatie se aduna si se scade jwMI2 se obtin ecuatiile: U1=(jwL1 - jwM)I1 + jwM (I1 + I2), U2= (jwL2 - jwM)I2 + jwM(I1 + I2) carora le corespunde schema echivalenta din figura b .
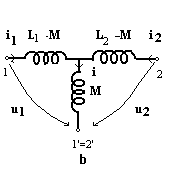
Acest procedeu se numeste spargerea cuplajului. Daca bornele polarizate sunt atacate diferit de curenti atunci M se inlocuieste cu -M si circuitul echivalent fara cuplaje este:
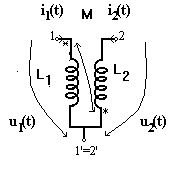
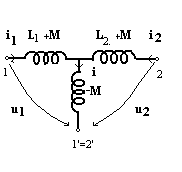
Daca sunt mai mult de doua bobine cuplate intre ele, circuitul echivalent in complex este asemanator. Iata un grup de trei bobine cuplate intre ele si circuitul echivalent in complex al
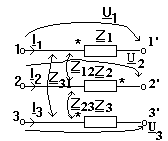
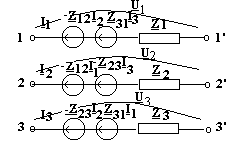
acestora. Se observa ca I1 si I3 intra in bornele polarizate in timp ce I2 iese din borna polarizata. Ca urmare impedantelor de comanda Z12 si Z23 li se va atasa semnul - iar impedantei de comanda Z31 i se va atasa semnul +.
4.4. Teoremele lui Kirchhoff in complex
Teorema I a lui Kirchhoff este :![]() si datorita liniaritatii reprezentarii in complex se obtine:
si datorita liniaritatii reprezentarii in complex se obtine:![]() (suma algebrica a curentilor in complex corespunzator
tuturor laturilor unei sectiuni S este nula).
(suma algebrica a curentilor in complex corespunzator
tuturor laturilor unei sectiuni S este nula).
Teorema a II-a a lui Kirchhoff este:![]() si similar rezulta
si similar rezulta![]() (suma algebrica a caderilor de tensiune complexe la bornele tuturor
elementelor de circuit care apartin aceleiasi bucle este nula).
(suma algebrica a caderilor de tensiune complexe la bornele tuturor
elementelor de circuit care apartin aceleiasi bucle este nula).
5. Puteri in circuitele de curent alternativ
Se
considera un EDC cu tensiunea si curentul la borne: u(t) = U![]() sinwt si i(t) = I
sinwt si i(t) = I![]() sin(wt - j). Pentru generatoare (surse) de
orice tip u(t) si i(t) sunt asociate dupa regula de la generatoare; pentru
celelalte elemente de circuit u(t) si i(t) sunt asociate dupa regula de la
receptoare. Se definesc urmatoarele puteri:
sin(wt - j). Pentru generatoare (surse) de
orice tip u(t) si i(t) sunt asociate dupa regula de la generatoare; pentru
celelalte elemente de circuit u(t) si i(t) sunt asociate dupa regula de la
receptoare. Se definesc urmatoarele puteri:
Puterea instantanee p(t), absorbita de receptor sau cedata de generator este:
p(t)= u(t) i(t) =2UI sinwt sin(wt - j) = UIcosj - UIcos(2wt - j)
Valoarea medie pe o perioada a puterii instantanei care se numeste putere activa P este:
![]()
Puterea activa depinde de valorile
efective ale tensiunii si curentului si de factorul
de putere ![]() si se consuma efectiv si ireversibil in rezistoare. Unitatea
de masura a puterii active este Wattul, [P] = 1W.
si se consuma efectiv si ireversibil in rezistoare. Unitatea
de masura a puterii active este Wattul, [P] = 1W.
Din
definitia puterii active rezulta interpretarea fizica a valorii efective a
curentului si a tensiunii. Daca se considera un rezistor cu rezistenta R prin
care trece curentul i(t) = I![]() sinwt rezulta u(t) = Ri(t) = RI
sinwt rezulta u(t) = Ri(t) = RI![]() sinwt si
sinwt si ![]() . Deci valoarea efectiva a unui curent sinusoidal este
numeric egala cu valoarea unui curent continuu care, trecand prin aceeasi
rezistenta ca si curentul sinusoidal produce aceeasi putere prin efect Joule.
. Deci valoarea efectiva a unui curent sinusoidal este
numeric egala cu valoarea unui curent continuu care, trecand prin aceeasi
rezistenta ca si curentul sinusoidal produce aceeasi putere prin efect Joule.
Puterea reactiva Q, este Q = UI sinj avand unitatea de masura [Q]=1VAR (volt-amper reactiv).
Puterea aparenta S, este S = UI si are unitatea de
masura [S] = 1VA. Evident ![]() .
.
Puterea aparenta complexa (puterea complexa) este S = U I*=UIej j =Uicosj +jUIsinj=P+jQ.
Puterile absorbite sau debitate de elementele ideale de circuit sunt:
- rezistorul ideal absoarbe puterea activa P=RI2 si, deoarece j=0, puterea reactiva absorbita este Q=UIsinj=0 deci puterea complexa absorbita este Sa =RI2 +j0.
-
bobina ideala parcursa de curentul i(t)=![]() Isinwt are tensiunea la borne u(t)=
Isinwt are tensiunea la borne u(t)= ![]() wLIsin(wt + p/2) deci j=p/2 si
rezulta Q=UIsinp/2=wLI²=U2/wL >
0, P = UI cosp/2 = 0, deci bobina absoarbe puterea complexa Sa=0+jwLI².
Media pe o perioda a energiei acumulate in bobina este
wLIsin(wt + p/2) deci j=p/2 si
rezulta Q=UIsinp/2=wLI²=U2/wL >
0, P = UI cosp/2 = 0, deci bobina absoarbe puterea complexa Sa=0+jwLI².
Media pe o perioda a energiei acumulate in bobina este ![]() .
.
-
condensatorul ideal cu tensiunea la borne u(t) = U![]() sinwt este parcurs de curentul i(t)=
sinwt este parcurs de curentul i(t)= ![]() wCUsin(wt + p/2), deci j = -p/2 si
rezulta Q = UIsin(-p/2)=
wCUsin(wt + p/2), deci j = -p/2 si
rezulta Q = UIsin(-p/2)= ![]() = - U²wC < 0, P = UI cos(-p/2) = 0,
deci condensatorul absoarbe puterea complexa Sa=0-jwCU².
Media pe o perioda a energiei acumulate in condensator este
= - U²wC < 0, P = UI cos(-p/2) = 0,
deci condensatorul absoarbe puterea complexa Sa=0-jwCU².
Media pe o perioda a energiei acumulate in condensator este ![]() .
.
Deoarece elementele dinamice condensator si bobina schimba cu circuitul in care sunt conectate o putere reactiva nenula, ele se numesc si elemente reactive.
-
sursa ideala de tensiune cu tensiunea electromotoare e(t)= ![]() Esinwt parcursa de curentul i(t)=
Esinwt parcursa de curentul i(t)= ![]() I sin(wt+j) debiteaza o putere complexa Sd=E
I* = EIe-jj = EIcosj-jEIsinj (U si I sunt asociate
dupa regula de la generatoare sau I parcurge sursa in sensul sagetii lui
E)
I sin(wt+j) debiteaza o putere complexa Sd=E
I* = EIe-jj = EIcosj-jEIsinj (U si I sunt asociate
dupa regula de la generatoare sau I parcurge sursa in sensul sagetii lui
E)
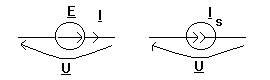
-
sursa ideala de curent cu curentul electromotor is(t)= ![]() Is sin(wt+j) cu tensiunea la borne u(t)=
Is sin(wt+j) cu tensiunea la borne u(t)= ![]() U sinwt debiteaza o putere complexa Sd
= U I* = UIse-jj = UIscosj-jUIssinj (U
si Is sunt asociate dupa regula de la generatoare)
U sinwt debiteaza o putere complexa Sd
= U I* = UIse-jj = UIscosj-jUIssinj (U
si Is sunt asociate dupa regula de la generatoare)
Observatii
i)puterea activa este absorbita numai de rezistoarele ideale
ii)puterea reactiva este absorbita numai de bobinele si condensatoarele ideale
iii)impedanta complexa Z=R+jX absoarbe puterea aparenta complexa Sa =U I*= Z I I*= ZI2=(R+jX) I2 =RI² + jXI² deci Pa=RI2 si Qa =XI2.
iv)sursele debiteaza atat putere activa cat si putere reactiva
6. Teorema conservarii puterilor complexe
Plecand de la teorema a II-a a lui Kirchhoff in complex (vezi paragraful 4.4) si de la faptul evident ca curentii conjugati Ik* verifica teorema I alui Kirchhoff in complex
![]() ) teorema lui Tellegen in complex este:
) teorema lui Tellegen in complex este:![]() ; in aceasta expresie
; in aceasta expresie
Teorema conservarii puterilor complexe Suma puterilor complexe debitate de toate sursele dintr-un circuit este egala cu suma puterilor complexe absorbite de toate impedantele din acelasi circuit:
![]()
Tinand seama ca :Sd = Pd + jQd si Sa = Pa + jQa rezulta:
![]() si
si
![]()
adica puterile active si puterile reactive se conserva.
Observatii:
i)puterile aparente Sk nu se conserva
ii)conservarea puterilor complexe poate fi folosita, similar cu consevarea puterilor in circuitele de c.c., la verificarea rezultatelor obtinute prin rezolvarea problemelor de analiza a circuitelor de c.a.
iii)tinand seama ca pentru o bobina Qa=w![]() si pentru un
condensator Qa=-w
si pentru un
condensator Qa=-w ![]() rezulta ca
rezulta ca ![]() deci un dipol RLC are
caracter inductiv daca
deci un dipol RLC are
caracter inductiv daca ![]() >0, are caracter capacitiv daca
>0, are caracter capacitiv daca ![]() <0 si are caracter rezistiv sau este la rezonanta (vezi
paragraful 4.9) daca
<0 si are caracter rezistiv sau este la rezonanta (vezi
paragraful 4.9) daca![]() =0
=0
iv)condensatorul nu genereaza putere reactiva chiar daca absoarbe o putere reactiva negativa; asa cum rezulta din teorema conservarii puterilor complexe, puterea reactiva (pozitiva sau negativa) este generata de surse
v)defazajul j intre
curent si tensiunea la bornele unui dipol RLC format din elemente de circuit cu
R,L,C>0 este cuprins intre -p/2 si +p/2 deoarece UIcosj=![]() deci cosj>0.
deci cosj>0.
7. Analiza circuitelor de curent alternativ
7.1. Introducere
Prin utilizarea reprezentarii in complex a marimilor sinusoidale, intr-un circuit de c.a. al carui graf are L laturi si N noduri se pot scrie urmatoarele ecuatii liniar independente intre ele:
N-1 ecuatii date de teorema I a lui Kirchhoff (vezi paragraful 1.3)
L-N+1 ecuatii date de teorema a II-a a lui Kirchhoff (vezi paragraful 1.3)
L ecuatii date de legaturile intre
Ecuatiile unui circuit de c.a. sunt ecuatii algebrice de aceeasi forma cu ecuatiile unui circuit liniar de c.c. deoarece:
- teoremele lui Kirchhoff au aceeasi forma
-
in ecuatiile de legatura intre
La
circuitele liniare de c.c. Ik si
7.2. Formularea problemei si metoda de rezolvare
Problema analizei unui circui de c. a. se formuleaza astfel:
se cunosc: valorile parametrilor elementelor (Rk, Lk, Ck, Mk, ek(t), isk(t)) si modul de interconectare a elementelor de circuit,
se cere sa se determine toate tensiunile si toti curentii.
Rezolvarea
acestei probleme consta in scrierea sistemului de 2L ecuatii ale circuitului si
determinarea solutiei acestuia (
Algoritmul de analiza a unui circuit de c.a. are urmatoarele etape:
1) Se construieste circuitul echivalent cu surse si impedante complexe utilizand schemele echivalente in complex ale elementelor de circuit
2) Se scriu ecuatiile acestui circuit
3)
Se rezolva sistemul de ecuatii si se determina valorile complexe ale curentilor
si tensiunilor, (
4) Se verifica rezultatele obtinute prin bilantul puterilor complexe
5)
Se determina valorile instantanee de forma ![]() sin(wt +jk).
sin(wt +jk).
Exemplu Fie circuitul din figura a cu e(t) =
30![]() sin wt
si is (t) = 2 sin (wt+p/4) unde w=100p s-1.
Circuitul echivalent cu surse si impedante complexe este dat in figura b.
sin wt
si is (t) = 2 sin (wt+p/4) unde w=100p s-1.
Circuitul echivalent cu surse si impedante complexe este dat in figura b.
Se scrie sistemul de ecuatii dat de teoremele lui Kirchhoff:
I1 + I2 = 1+j , 10 I1 -20j I2 = 30, 20j I2 - 20j (1+j) - U = 0
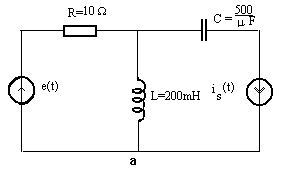
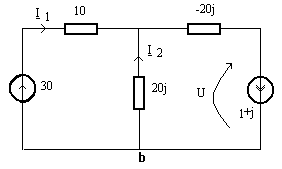
Solutiile acestui sistem sunt: I1 = 1 , I2 = j si U = - 20j.
Verificarea rezultatelor prin bilantul puterilor complexe:
![]() = E I1* + U Is*
= 301 + (-20j) (1-j) = 10 -20j
= E I1* + U Is*
= 301 + (-20j) (1-j) = 10 -20j
![]() = RI12 + wLjI22
-
= RI12 + wLjI22
-![]() jIs2 = 101 + 20j1- 20j2 = 10 - 20j
jIs2 = 101 + 20j1- 20j2 = 10 - 20j
Valorile instantanee sunt: i1
(t) = ![]() sin wt,
i2 =
sin wt,
i2 = ![]() sin( wt+p/2) si u(t) = 20
sin( wt+p/2) si u(t) = 20![]() sin( wt-p/2)
sin( wt-p/2)
7. Scrierea ecuatiilor potentialelor nodurilor si curentilor ciclici
7.1. Metoda potentialelor nodurilor
Asa cum s-a aratat in paragraful 2.5.1 se prefera comanda in tensiune deoarece marimea de comanda poate fi scrisa ca o diferenta de potentiale. Ca urmare, circuitul echivalent cu surse de tensiune comandate in curent al bobinelor cuplate (vezi paragraful 4.3) nu este potrivit pentru scrierea ecuatiilor metodei nodale. Pentru aceste bobine se poate construi un circuit echivalent cu surse de curent comandate in tensiune. In acest scop se rezolva ecuatiile de functionare ale bobinelor cuplate: U1=jwL1I1jwMI2 , U2=jwL2I2jwMI1 in raport cu necunoscutele I1 si I2 .
Exemplu. Fie bobinele cuplate cu ecuatiile de functionare![]()
![]()
Rezolvand acest sistem de ecuatii in raport cu I1 si I2 rezulta:
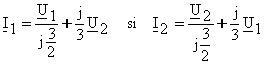
adica ecuatiile urmatorului circuit echivalent:
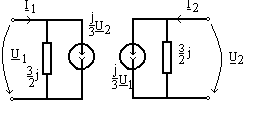
Aplicatie .Sa se scrie ecuatiile potentialelor nodurilor pentru circuitul:
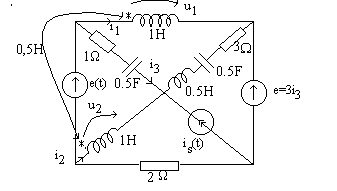
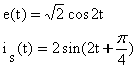
Deoarece cuplajul nu se poate sparge construim circuitul echivalent cu
surse de curent comandate in tensiune al celor doua bobine cuplate. Cu notatiile
din figura ecuatiile de functionare ale acestor doua bobine sunt: ![]() deci circuitul
echivalent este cel prezentat in exemplul precedent. Schema echivalenta in
complex este:
deci circuitul
echivalent este cel prezentat in exemplul precedent. Schema echivalenta in
complex este:
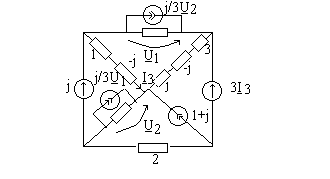
Se observa ca avem un circuit rezonant RLC serie cu Ze = j-j+3 =3 si doua surse ideale de tensiune care nu se pot transforma in surse de curent. Alegem ca potential de referinta o borna a uneia
dintre aceste surse iar pentru cealalta introducem necunoscuta suplimentara I4 . Rezulta ecuatiile
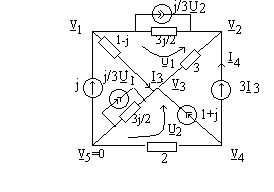
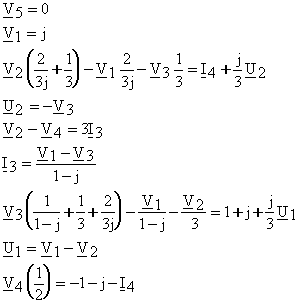
adica un sistem de 9 ecuatii cu
necunoscutele ![]()
Deci algoritmul de scriere a ecuatiilor potentialelor nodurilor este:
se fac toate transformarile posibile ale surselor de tensiune in surse de curent si ale comenzilor in curent in comenzi in tensiune
se alege potentialul de referinta astfel incat cat mai multe potentiale ale nodurilor sa poata fi exprimate ca sume de tensiuni electromotoare
considerand si necunoscutele suplimentare (curentii unor surse de tensiune conectate intre alte noduri decat cele de la punctul precedent si curenti de comanda) se scrie sistemul de ecuatii:
![]()
si ecuatiile suplimentare
7.2. Metoda curentilor ciclici
Aplicatie. Sa se scrie ecuatiile metodei curentilor ciclici pentru circuitul:
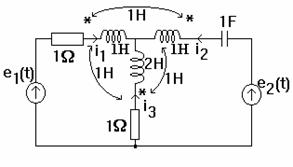
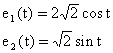
Schema echivalenta in complex se construieste considerand pentru bobine circuitul echivalent cu surse de tensiune comandate in curent (vezi paragraful 4.2).
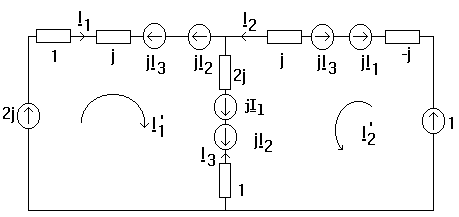
Rezulta ecuatiile 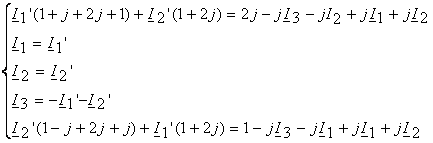
deci 5 ecuatii cu necunoscutele ![]()
Deci algoritmul de scriere a ecuatiilor curentilor ciclici este:
se fac toate transformarile posibile ale surselor de curent in surse de tensiune si ale comenzilor in tensiune in comenzi in curent
se aleg cele B=L-N + 1 bucle fundamentale astfel incat sursele de curent netransformate sa fie plasate in coarbore
considerand ca aceste bucle sunt
parcurse de niste curenti fictivi ![]() (curentii ciclici), se
aleg sensurile acestora si se scrie sistemul de ecuatii:
(curentii ciclici), se
aleg sensurile acestora si se scrie sistemul de ecuatii:
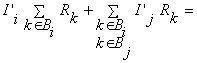
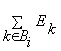
si ecuatiile suplimentare
8. Teoreme ale circuitelor de curent aternativ
Ecuatiile circuitului echivalent cu surse si impedante complexe sunt similare ecuatiilor unui circuit liniar de curent continuu (vezi paragraful 4.7.1). Din acest motiv enunturile teoremelor sunt asemanatoare cu cele din paragraful 2.4 si demonstratiile nu vor fi reluate.
4.8.1. Teoremele impedantelor echivalente
Legarea in serie a impedantelor: ![]() . Deoarece Zes = Res + jXes
si Zk = Rk + jXk rezulta
. Deoarece Zes = Res + jXes
si Zk = Rk + jXk rezulta ![]() si
si 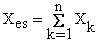
Legarea in paralel a impedantelor: ![]() , deci
, deci ![]() si
si ![]()
8.2. Teorema superpozitiei
Fie un circuit de c.a. cu mai multe surse: E1, , El, Is,l+1,,Ism. Orice curent (sau tensiune) din circuit se poate scrie ca o suma a curentilor (tensiunilor) din aceeasi latura produsi de fiecare sursa independenta separat, celelalte surse independente fiind pasivizate.
De
exemplu ![]() unde I1k
este curentul produs in latura 1 de sursa independenta din latura k, celelalte
surse independente fiind pasivizate.
unde I1k
este curentul produs in latura 1 de sursa independenta din latura k, celelalte
surse independente fiind pasivizate.
Teorema este o consecinta a caracterului liniar al ecuatiilor circuitului. Sursele comandate nu se pasivizeaza.
8. Teoremele generatoarelor echivalente
Generatorul echivalent de tensiune al unui dipol Fie un dipol liniar cu bornele A si B.
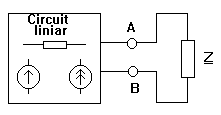
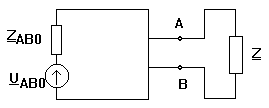
Oricat de complicat ar fi acest circuit el se poate echivala cu un circuit format dintr-o sursa de tensiune UAB0 in serie cu o impedanta ZAB0 unde UAB0 este tensiunea de mers in gol masurata la bornele A si B (impedanta Z fiind scoasa din circuit) si ZAB0 este impedanta echivalenta intre
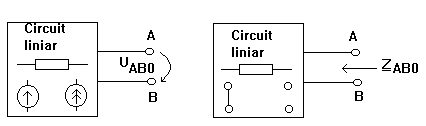
bornele A si B a circuitului pasivizat (sursele comandate nu se pasivizeaza).
Daca
circuitul pasivizat este o combinatie serie - paralel de impedante atunci
determinarea lui ZAB0 se poate face cu regulile din
paragraful 4.8.1. Daca circuitul contine surse comandate sau nu este un circuit
serie - paralel, atunci se conecteaza intre A si B o sursa independenta de
tensiune de valoare 1V ( sau o sursa independenta de curent de valoare 1A) si ZAB0 rezulta in urma determinarii lui I
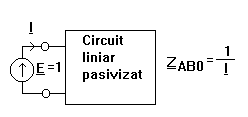
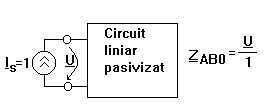
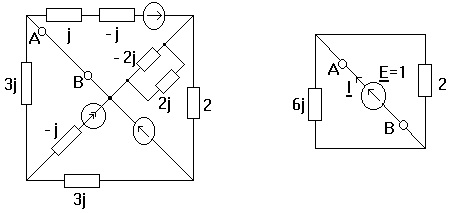
Aplicatie. Sa se calculeze ![]()
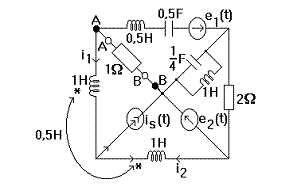
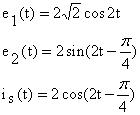
Bobinele cuplate avand
un nod comun se poate sparge cuplajul. Prin pasivizare si calculand impedantele
echivalente ![]() circuitul capata o
forma mai simpla. Se conec- teaza intre A si B o sursa de tensiune cu
circuitul capata o
forma mai simpla. Se conec- teaza intre A si B o sursa de tensiune cu ![]() si rezulta
si rezulta
![]()
Generatorul echivalent de curent al unui dipol Fie un dipol liniar cu bornele A si B

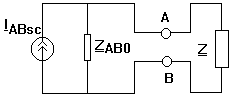
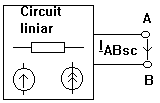
Oricat de complicat ar fi acest circuit el se poate echivala cu un circuit format dintr-o sursa de curent IABsc in paralel cu o impedanta ZAB0 unde curentul IABsc corespunde scurtcircuitului intre bornele A si B.
Daca in schemele echivalente ale diportilor rezistivi liniari (vezi paragraful 2.4.) se inlocuiesc rezistentele cu impedante si conductantele cu admitante se obtin schemele echivalente ale diportilor de c.a
8.4. Teorema transferului maxim de putere activa
Se considera o sursa de tensiune electromotoare E si de impedanta interna Zi, la bornele careia se leaga o impedanta Z. Se pune problema urmatoare: ce relatie trebuie sa existe intre Zi si Z astfel incat pentru un E dat puterea activa absorbita de Z sa fie maxima.
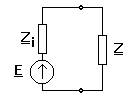
Fie Zi = Ri
+ jXi si Z = R + jX . Curentul din circuit este ![]() si deci puterea activa
absorbita de Z este
si deci puterea activa
absorbita de Z este 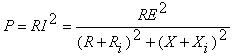
Se observa ca functia P(R,X) are un
maxim in raport cu X pentru X= -Xi . Valoarea acestui maxim este 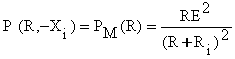 . Maximul functiei
. Maximul functiei ![]() are loc pentru R=Ri
(vezi teorema transferului de putere in curent continuu). Rezulta ca puterea activa absorbita de sarcina este
maxima daca Z = Zi* (teorema transferului maxim de putere
activa).
are loc pentru R=Ri
(vezi teorema transferului de putere in curent continuu). Rezulta ca puterea activa absorbita de sarcina este
maxima daca Z = Zi* (teorema transferului maxim de putere
activa).
Daca Z = Zi* puterea activa Pd cedata de sursa este consumata in cantitati egale de R si Ri deci randamentul circuitului este h=P/ Pd=0,5.
Observatii
i) daca R¥ si/sau X¥ atunci h1 dar P0
ii) daca in loc de sursa de tensiune avem o sursa de curent cu parametrii Is si Zi, impedanta de sarcina Z absoarbe puterea activa maxima tot daca Z = Zi*
iii) daca generatorul de curent alternativ are o impedanta interna inductiva, rezulta ca pentru a absorbi o putere activa maxima sarcina trebuie sa aiba un caracter capacitiv.
9. Rezonanta dipolilor
9.1. Definitii si exemple
Exista doua definitii ale rezonantei: prima se foloseste in electroenergetica, a doua se utilizeaza la circuitele electronice.
Definitia 1 Un dipol de c.a. este la rezonanta daca absoarbe pe la borne o putere reactiva nula,
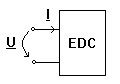
adica Qabs=UI sinj = 0.
Deci la rezonanta defazajul j dintre U si I este nul (sinj = 0 Þ j = 0). Daca impedanta echivalenta la bornele dipolului este Z=R+jX, Q=XI² =0 ÞX = 0 deci la rezonanta reactanta echivalenta este nula si dipolul are o comportare rezistiva la borne.
Definitia 2 a)
Se considera la bornele dipolului o sursa de tensiune cu pulsatie variabila si
valoare efectiva
Exemplu
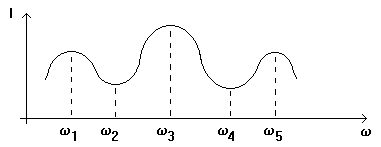
- dipolul este la rezonanta pentru pulsatiile w1 , w2 , w3 , w4, w5
- in cazul maximelor de curent (w1 , w3 , w5 ) avem rezonanta de tensiune,
- in cazul minimelor de curent (w2 , w4) avem rezonanta de curent.
Se observa ca deoarece I = Y U si U = ct, curba Y (w) are aceeasi alura cu I (w).
b) Se considera la bornele dipolului o
sursa de curent cu pulsatie variabila si valoare efectiva
Exemplu
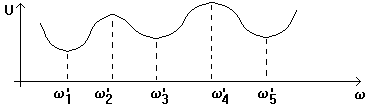
- dipolul este la rezonanta pentru pulsatiile w'1 , w'2 , w'3 , w'4, w'5
- in cazul minimelor de tensiune (w'1 , w'3 , w'5) avem rezonanta de tensiune,
- in cazul maximelor de tensiune (w'2 , w'4) avem rezonanta de curent.
Deoarece U = Z I si I = ct, curba Z(w) are aceeasi alura cu U(w).
Observatii
i) cele doua definitii ale rezonantei nu duc in general la aceleasi pulsatii de rezonanta
ii) rezonanta de tensiune are loc la pulsatiile pentru care Y(w) are maxime locale si deci Z(w)=1/ Y(w) are minime locale
iii) rezonanta de curent are loc la pulsatiile pentru care Y(w) are minime locale si deci Z(w)=1/ Y(w) are maxime locale.
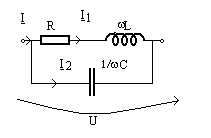
Exemple. a)
![]()
Se
calculeaza puterea aparenta complexa S = UI* si se anuleaza
puterea reactiva obtinandu-se pulsatiile de rezonanta dupa definitia 1: 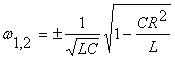
![]() ; se observa ca daca R0
; se observa ca daca R0
atunci w2![]() . Se calculeaza minimele si maximele lui I(w)
respectiv ale lui Z(w)
. Se calculeaza minimele si maximele lui I(w)
respectiv ale lui Z(w)
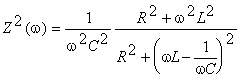 si
si ![]() are solutiile
are solutiile 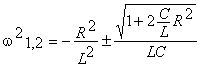
(daca R0 atunci w2![]() ). Pulsatiile de rezonanta obtinute dupa cele doua definitii
nu sunt aceleasi.
). Pulsatiile de rezonanta obtinute dupa cele doua definitii
nu sunt aceleasi.
b) Impedanta complexa a circuitului
RLC serie este ![]() . Rezulta
. Rezulta
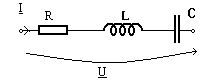
![]() . Dupa prima definitie, pulsatia de rezonanta corespunde lui
X=0 deci
. Dupa prima definitie, pulsatia de rezonanta corespunde lui
X=0 deci ![]() . Dupa a doua definitie, se calculeaza
. Dupa a doua definitie, se calculeaza ![]() si se obtine aceeasi
valoare pentru w0 . Daca U=ct in raport cu w, la
rezonanta I ia valoarea maxima deoarece Z ia valoarea minima Z(w0)=R..
Pentru acest circuit Uc(w0)=|Xc|I= UL(w0)=|XL|I
si Uc(w0)= -UL(w0) deci U(w0)=UR(w0) +UC(w0) + UL(w0)=UR(w0). Este
posibil ca la rezonanta si in jurul pulsatiei de rezonanta UC si UL
sa aiba valori mai mari decat tensiunea U a sursei de alimentare. Se noteaza cu
si se obtine aceeasi
valoare pentru w0 . Daca U=ct in raport cu w, la
rezonanta I ia valoarea maxima deoarece Z ia valoarea minima Z(w0)=R..
Pentru acest circuit Uc(w0)=|Xc|I= UL(w0)=|XL|I
si Uc(w0)= -UL(w0) deci U(w0)=UR(w0) +UC(w0) + UL(w0)=UR(w0). Este
posibil ca la rezonanta si in jurul pulsatiei de rezonanta UC si UL
sa aiba valori mai mari decat tensiunea U a sursei de alimentare. Se noteaza cu
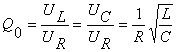 factorul de calitate
al circuitului unde UL, UC,
factorul de calitate
al circuitului unde UL, UC, ![]() ), la rezonanta, tensiunea bobinei si cea a condensatorului
depasesc tensiunea sursei de alimentare.
), la rezonanta, tensiunea bobinei si cea a condensatorului
depasesc tensiunea sursei de alimentare.
c)
Circuitul RLC paralel are propietati selective in frecventa duale celui RLC
serie. 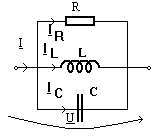
Utilizand
ambele definitii se obtine aceeasi pulsatie de rezonanta a acesui circuit ![]() . La rezonanta
. La rezonanta 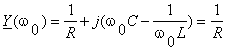 deci Y are valoarea
minima. Daca U=ct in raport cu w, la rezonanta I ia valoarea minima deoarece I=YU. Pentru
acest circuit Ic(w0)=U/|Xc|= IL(w0)=U/|XL|
si Ic(w0)= -IL(w0) deci I(w0)=IR(w0) +IC(w0) + IL(w0)=IR(w0). Este
posibil ca la rezonanta si in jurul pulsatiei de rezonanta IC si IL
sa aiba valori mai mari decat curentul I prin sursa de alimentare. Se noteaza
cu Q0 factorul de calitate
deci Y are valoarea
minima. Daca U=ct in raport cu w, la rezonanta I ia valoarea minima deoarece I=YU. Pentru
acest circuit Ic(w0)=U/|Xc|= IL(w0)=U/|XL|
si Ic(w0)= -IL(w0) deci I(w0)=IR(w0) +IC(w0) + IL(w0)=IR(w0). Este
posibil ca la rezonanta si in jurul pulsatiei de rezonanta IC si IL
sa aiba valori mai mari decat curentul I prin sursa de alimentare. Se noteaza
cu Q0 factorul de calitate 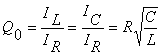 unde IL, IC,
IR se considera la rezonanta. Daca Q0 >1 (
unde IL, IC,
IR se considera la rezonanta. Daca Q0 >1 (![]() ),curentul bobinei si al condensatorului depasesc curentul
total.
),curentul bobinei si al condensatorului depasesc curentul
total.
9.2. Aplicatii tehnice ale rezonantei
a)Compensarea factorului de putere Presupunem ca avem o linie de transport al energiei electrice la capatul careia este conectat consumatorul inductiv (asa cum sunt majoritatea consumatorilor energetici) din figura a..
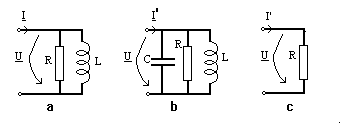
Curentul
absorbit de consumator este :![]() deci
deci 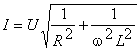 si cosj =
si cosj =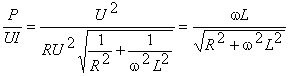 .
.
Se conecteaza un condensator in
paralel cu consumatorul astfel incat ![]() (circuitul b). In
acest caz avem un circuit RLC derivatie la rezonanta a carui impedanta de
intrare este Z=R si curentul absorbit de receptor este
(circuitul b). In
acest caz avem un circuit RLC derivatie la rezonanta a carui impedanta de
intrare este Z=R si curentul absorbit de receptor este ![]() . Puterea reactiva absorbita de consumatorul inductiv in
paralel cu condensatorul C este nula, si pierderile de putere activa pe linia
de transport (de rezistenta r ) vor fi minime : DP'linie = rI'2 < DPlinie=
rI2. In acest caz factorul de putere cosj'=1 si
avem o compensare totala a factorului de
putere.
. Puterea reactiva absorbita de consumatorul inductiv in
paralel cu condensatorul C este nula, si pierderile de putere activa pe linia
de transport (de rezistenta r ) vor fi minime : DP'linie = rI'2 < DPlinie=
rI2. In acest caz factorul de putere cosj'=1 si
avem o compensare totala a factorului de
putere.
Consumatorii industriali nu au tot
timpul aceiasi parametri (se opresc anumite utilaje, in anumite zile nu se
lucreaza, etc). Pentru a nu se ajunge la functionarea in regim capacitiv (care
produce efecte nedorite in sistem) mentinand pierderile de putere pe linie la
un nivel rezonabil se face o compensare
partiala a factorului de putere (de exemplu cosj'=0,92).
In acest caz calculul capacitatii condensatorului care se leaga in paralel cu
consumatorul inductiv se face astfel: diferenta intre puterea reactiva
absorbita de consumatorul necompensat Q=UIsinj si cea absorbita de consumatorul compensat partial
Q'=UIsinj' este absorbita de condensator (QC=wCU2).
Exprimand puterile reactive in functie de puterea activa P absorbita de
consumator (Q=Ptgj, Q'=Ptgj') rezulta ![]() . In acest calcul se considera ca U nu se modifica prin
. In acest calcul se considera ca U nu se modifica prin
conectarea condensatorului.
b) Montaje Boucherot
Se considera cele doua circuite din figura de mai jos. Daca parametrii bobinei si condensatorului indeplinesc conditia de rezonanta (w2 LC = 1) atunci curentul prin impedanta Z are valoarea U/wL pentru primul circuit si UwC pentru al doilea circuit, deci este independent de valoarea lui Z .
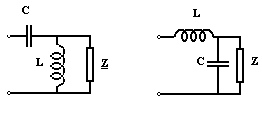
Aceasta proprietate se poate verifica foarte usor.
c)Circuite
de rezistenta
Impedanta de intrare intr-un astfel de circuit nu depinde de frecventa, desi circuitul contine si elemente reactive. Cele doua circuite din figura de mai jos au Z=R atunci cand parametrii
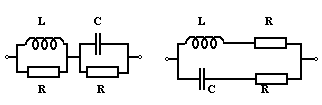
indeplinesc conditia: R2 = L/C. Verificarea acestei propietati este un exercitiu simplu.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4231
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved