| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
Constructia si functionarea filtrelor electrostatice.
Principiul de functionare
Functionarea filtrelor electrostatice se bazeaza pe actiunea fortelor electrice care sunt exercitate asupra particulelor incarcate cu sarcina electrica prin intermediul unui camp electric. Spre deosebire de mijloacele de filtrare clasice (de exemplu filtrele mecanice care utilizeaza fortele de inertie sau cele centrifuge), in precipitatoarele electrostatice, fortele separatoare actioneaza direct asupra particulelor ce trebuiesc retinute.
Fie un filtru electrostatic din cele mai simple, construit dintr-un cilindru legat la pamant si un fir plasat in axa centrala a cilindrului (Figura 1).
V0
Gaz particule incarcate
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Figura - Reprezentarea schematica a unui filtru electrostatic simplu.
Daca firul central este conectat la un potential electric inalt (zeci de kilovolti), la suprafata acestuia se produce o descarcare corona si ionii care au aceasi polaritate ca firul sunt antrenati catre cilindru. Acest fenomen conduce la formarea unei sarcini ionice cu o densitate mare la capatul firului si care descreste de-a lungul suprafetei cilindrului.
O parte dintre acesti ioni sunt captati de particule din cauza distorsiunii locale a campului electric datorata diferentei de valoare intre permitivitatea relativa a particulelor si cea a gazului. Astfel, particulele se incarca prin captarea ionilor pana la o sarcina maxima (limita). Particulele incarcate sunt supuse unei forte electrice dirijata de-a lungul suprafetei cilindrului exterior conectat la pamant. Ele formeaza un strat care se poate inlatura pe cale mecanica (Figura 2).
Functionarea
electrofiltrelor este determinata atat de parametri electrici
(distributia campului electric ![]() , distributia curentului electric in spatiul
interelectrodic
, distributia curentului electric in spatiul
interelectrodic ![]() ), cat si de proprietatile gazului de lucru
si mai ales cele ale particulelor separate (rezistivitatea electrica,
permitivitatea electrica er, talia particulelor
), cat si de proprietatile gazului de lucru
si mai ales cele ale particulelor separate (rezistivitatea electrica,
permitivitatea electrica er, talia particulelor ![]() ).
).
Tipuri de electrofiltre
Electrofiltre cu un singur etaj
Datorita constructiei lor simple si a robustetei, aceste electrofiltre sunt utilizate in aplicatii industriale. Incarcarea si captarea particulelor sunt realizate simultan in aceeasi regiune a electrofiltrului.

Figura - Principalele etape care intervin in functionarea unui electrofiltru
Cele mai raspandite electrofiltre din aceasta categorie sunt cele tip placa-placa. Aici, electrozii de depunere sunt placi paralele si echidistante iar gazul este ionizat cu ajutorul electrozilor ionizanti situati in planul vertical, la jumatatea distantei dintre placi. O astfel de pereche de electrozi de captare plani, intre care se gaseste un anumit numar de electrozi de ionizare constituie o celula de filtrare. Fiecare sectiune de filtrare (flux sau camp) este alcatuita dintr-un mare numar de astfel de celule, in functie de aplicatia la care este utilizat precipitatorul, si are propria sa alimentare electrica, independenta de alte parti ale filtrului. Acest lucru permite adaptarea conditiilor electrice in functie de marimea si concentratia particulelor prezente in fiecare camp.
In cazul precipitatorului fir-cilindru, electrodul ionizant este plasat in lungul axei cilindrului asezat in pozitie verticala. In cazul acestor electrofiltre, stratul de particule format pe fata interioara a cilindrului este inlaturat prin intermediul unui film lichid. Astfel, patura de particule se detaseaza si sub influenta gravitatiei cade in buncarele situate in partea inferioara a cilindrului. Din acest motiv, filtrele de acest tip sunt utilizate in cazul filtrarii particulelor lichide.
In general, un precipitator electrostatic poate fi alimentat cu un potential electric de polaritate pozitiva sau negativa. Totusi, pentru o anumita configuratie de electrozi, valoarea potentialului electric de la care se produce amorsarea descarcarii corona, cat si cea a potentialului de strapungere a spatiului dintre electrozi, sunt mai mari in polaritate negativa (cativa zeci de kilovolti). Pentru obtinerea unui maxim al intensitatii campului electric si al eficacitatii colectarii, electrozii de ionizare ai filtrelor industriale sunt pusi la un potential negativ iar placile colectoare sunt legate la pamant. Astfel, are loc o puternica ionizare a gazului portor ceea ce conduce la formarea unei sarcini ionice spatiale foarte dense, si la o buna incarcare cu sarcina electrica a particulelor.
Electrofiltre cu doua etaje
Aceste filtre prezinta o structura mai complicata si au dimensiuni mai reduse. Sunt utilizate in principal pentru filtrarea aerului ambiant din anumite cladiri si hale de productie.
Cele doua sectiuni ale unui astfel de filtru sunt alimentate separat cu tensiune, acest lucru necesitand in general o sursa dubla de tensiune cat si cabluri electrice separate.

Figura 3. - Vedere schematica a unui filtru electrostatic: a) tip placa-placa ;
b) tip fir-cilindru
Figura 4 prezinta un precipitator cu doua etaje cu electrozii colectori sub forma de placi. Primul etaj, ce poarta denumirea de etaj de incarcare (sau etaj ionizator), are electrozii de descarcare sub forma de fir sau de benzi. Electrozii colectori pot avea forma placilor paralele si echidistante sau forma unor cilindrii coaxiali.
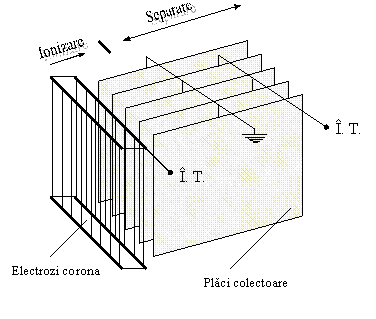

Figura 4. - Vedere sistematica a unui precipitator electrostatic dublu etaj si electrozi colectori plani
Tabel - Marimi caracteristice pentru precipitatoare plane si tubulare [1,2].
|
Marime caracteristica |
Precipitator tub - fir |
Precipitator placa - fir |
|
Viteza gazelor v [m/s] | ||
|
Distanta intre placi sau diametrul cilindrului 2Rc [mm] | ||
|
E [KV/cm] | ||
|
Densitatea de curent JC [mA/m2] | ||
|
Eficienta
de colectare | ||
|
Aplicatii |
Industria chimica, Hidrocarburi |
Centrale termoelectrice Metalurgie, Ciment |
3. Electrofiltre cu electrozi de depunere umezi
In cazul precipitatoarelor electrostatice uzuale exista o valoare a rezistivitatii particulelor peste care performantele de separare scad ceea ce duce la reantrenarea particulelor colectate, in interiorul electrofiltrelor. Pentru a impiedica acest fenomen, s-au construit anumite electrofiltrele ce utilizeaza un film de apa cu ajutorul caruia se umezesc depunerile de pe suprafata electrozilor colectori. Realizarea tehnica a filtrului este mai complicata datorita sistemului necesar pentru pomparea si distributia apei. Electrofiltrele cu film de apa sunt prezente in anumite aplicatii speciale datorita unor avantaje printre care cele mai importante sunt: randamentul filtrarii este superior; reantrenarea particulelor colectate este imposibila (particulele ce se depun pe suprafetele colectoare, datorita umezirii, se descarca complet nemaiputand astfel sa reintre in circuit); performantele de separare sunt independente de rezisitivitatea depunerilor, etc.
Miscarea particulelor in interiorul unui filtru electrostatic depinde de mai multi factori, de obicei grupati in doua categorii:
cei de natura electrica (distributia campului electric, densitatea si repartitia sarcinii ionice spatiale dintre electrozi) - ce determina intr-o buna masura o alta marime esentiala ce intervine in procesul de separare electrostatica si anume, sarcina electrica acumulata de particule in cursul deplasarii lor in interiorul precipitatorului, si
cei care reunesc toate caracteristicile curgerii gazului - factori aerodinamici: diferenta de presiune intre intrarea si iesirea electrofiltrului, gradul de turbulenta a gazului etc. Cercetarile realizate pana in prezent indica faptul ca structura de curgere a gazului este specifica fiecarui electrofiltru in parte. Studiul aspectelor aerodinamice necesita o buna cunoastere a dependentelor existente intre structura de curgere a gazului si fenomenele legate de producerea descarcarilor corona (injectia de sarcina ionica, repartitia campului electric, etc.). Ciocnirile intre moleculele neutre de gaz si ionii accelerati de campul electric conduc la aparitia asa numitului fenomen de vant ionic - o miscare a gazului orientata dinspre planul electrozilor de ionizare catre placile colectoare.
In prezenta curgerii principale a gazului (data de gradientul de presiune intrare-iesire), fortele electrice ce se exercita asupra ionilor si particulelor incarcate cu sarcina determina aparitia unei curgeri secundare a gazului. Miscarea rezultanta a gazului in precipitator este, deci, rezultatul interactiunii dintre curgerea primara si aceasta curgere secundara data de densitatea de volum a fortei electrice.
Aceasta curgere foarte complexa a gazului portor are o influenta mare asupra procesului de incarcare cu sarcina electrica a particulelor si, deci, in final, asupra captarii particulelor.
Conditiile electrice depind de forma geometrica a electrozilor si de polaritatea potentialului aplicat. Campul electric intens din vecinatatea acestor electrozi conduce la aparitia descarcarilor corona responsabile de crearea sarcinii spatiale ionice.
Calculul unei sarcini electrice a unei particule necesita cunoasterea intensitatii campului electric, a densitatii sarcinii libere cat si a altor factori care pot influenta traiectoria acestei particule. Exista mai multe modele ce permit calculul sarcinii unei particule sferice, dar, deocamdata, masurarile experimentale ce permit calibrarea acestor modele nu sunt foarte precise.
In momentul de fata se cunosc doi parametri principali care influenteaza direct eficacitatea colectarii: viteza medie a gazului si intensitatea turbulentei. Turbulenta nu este generata doar de diferenta de presiune la intrarea si iesirea din filtru, ci si de fenomenele asociate descarcarilor corona si miscarii particulelor in camp electric.
Ciocnirile dintre moleculele neutre de gaz si ionii accelerati de campul electric determina in absenta curgerii axiale a gazului aparitia vantului ionic - o miscare a gazului de la electrozii ionizati catre placile colectoare. Curgerea rezultanta a gazului va fi, in consecinta, rezultatul interactiunii celor doua. Momentan, intensitatea turbulentei este adesea calculata sau masurata in situatiile particulare care insa ofera informatii relativ restranse valabile in cazul precipitatoarelor industriale.
Avand la baza aceste principii cat si observarea directa a functionarii catorva filtre electrostatice, s-au elaborat mai multe modele de studio a functionarii precipitatoarelor electrostatice. In trecut, au fost create modele teoretice simple care au fost utilizate mai bine de o jumatate de secol pentru proiectarea si dimensionarea electrofiltrelor. Odata cu dezvoltarea instrumentelor de calcul, au fost elaborate modele mai rafinate, care iau in considerare mai multe fenomene prezente in procesul de filtrare electrostatica.
In urma celor amintite mai sus, retinem cateva observatii mai importante care vor fi avute in vedere in continutul acestei lucrari:
precipitatoarele electrostatice reunesc fenomene electrice, aerodinamice si mecanice strans legate intre ele;
simularea functionarii unui electrofiltru necesita crearea unor modele care permit calculul ansamblului de marimi electrice si aerodinamice.
Influenta repartitiei gazului
Studiile
experimentale asupra functionarii electrofiltrelor au permis punerea
in evidenta a influentei vitezei gazului asupra
performantelor de filtrare. Astfel, o repartitie neuniforma a
curentilor de gaz poate duce la viteze locale mari si astfel la zone
cu eficacitate redusa. Dupa Bump [3], nimic nu poate reduce
performantele unui filtru mai mult decat repartitia neuniforma a
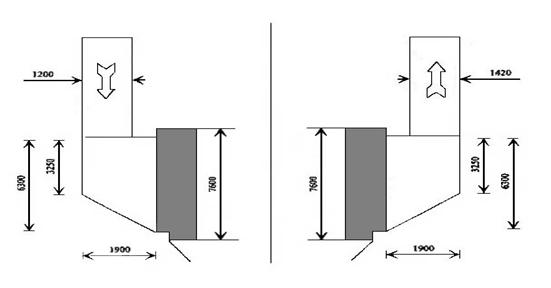
gazului. Ori, majoritatea instalatiilor industriale prezinta
obstacole in amonte de filtru (Figura 1),
favorizand astfel o distributie aerodinamica neuniforma. Pentru
a reduce aceasta problema, se folosesc grilaje de ghidare puse la
intrarea in electrofiltru cu scopul de a redresa curentii de gaz [4].
Figura - Forma conductelor situate la intrarea si iesirea electrofiltrului.
Pe langa cresterile foarte mari ale vitezei locale a gazului care pot sa apara in anumite puncte, o repartitie neuniforma a gazului poate duce la o slabire a performantelor filtrului astfel:
o repartitie neuniforma a concentratiei de particule, ce duce la o aglomerare locala a impuritatilor in zonele in care viteza gazului este mare si, implicit, rezulta o scadere a performantelor de filtrare [4];
cresterea riscului de reantrenare a particulelor datorita fortelor locale de smulgere [4]. Dupa Bump [3], in anii 60-70, o treime din particulele tratate au fost reantrenate in filtre datorita repartitiei neuniforme a gazului. Pentru a minimaliza acest efect, s-a modificat geometria electrodului colector ca in Figura
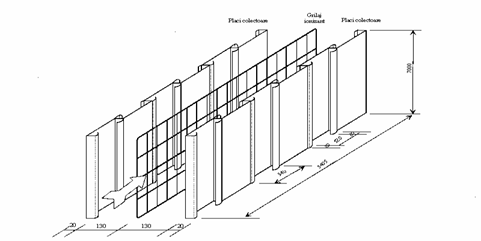
Figura - Schema conductelor de la intrarea si iesirea din electrofiltru.
Conform Griesco & Fortune [5], in practica, curgerea gazului in interiorul unui electrofiltru se considera ca fiind in parametri optimi daca 85 % dintre vitezele locale (ale particulelor fluide) au o abatere de 25% fata de viteza medie (integrata pe toata sectiunea transversala a electrofiltrului) de curgere a gazului si daca nici una dintre acestea nu depaseste o abatere maxima de 40% din viteza medie.
Influenta stratului de particule colectate asupra functionarii electrofiltrelor
Fenomenele ce au loc in stratul de particule colectate prezinta o importanta majora, acestea facand obiectul a numeroase studii teoretice si experimentale.
Pentru ca particulele aflate in camp electric sa se depuna pe electrozii colectori, este necesar ca acestea sa fie suficient de aderente intre ele si cu peretii electrozilor. Stratul de particule depuse scade numarul de ioni formati intr-o prima faza si se opune creeri de noi ioni intr-o a doua faza, printr-un fenomen ce poarta numele de contra-emisie.
Caderea de tensiune datorata prezentei stratului de particule depus pe electrozii colectori este:
![]() , (1)
, (1)
unde: ![]() reprezinta
rezistivitatea stratului depus,
reprezinta
rezistivitatea stratului depus, ![]() grosimea acestuia
si
grosimea acestuia
si ![]() densitatea curentiului
ionic.
densitatea curentiului
ionic.
Pentru particule cu rezistivitatea
scazuta, functionarea filtrului nu este foarte mult
afectata. Totusi, prin cresterea ![]() , ionii creati de descarcarea corona sunt mai greu
"evacuati" catre electrozii de colectare ceea ce duce la "acumularea" unei
sarcini electrice in stratul de particule depus. Pentru rezistivitati
ridicate ( ρ
, ionii creati de descarcarea corona sunt mai greu
"evacuati" catre electrozii de colectare ceea ce duce la "acumularea" unei
sarcini electrice in stratul de particule depus. Pentru rezistivitati
ridicate ( ρ![]()
![]() ) se poate produce o scadere a tensiunii de mai
multi kilovolti de indata ce grosimea paturii ajunge la
cativa milimetri (densitatile uzuale de curent sunt cuprinse
intre 0,1 si 0,5 mA/m2).
In acest caz, se poate ca descarcarea corona sa inceteze
datorita faptului ca intensitatea campului electric nu este
sufficient de mare pentru a intretine multiplicarea electronica.
) se poate produce o scadere a tensiunii de mai
multi kilovolti de indata ce grosimea paturii ajunge la
cativa milimetri (densitatile uzuale de curent sunt cuprinse
intre 0,1 si 0,5 mA/m2).
In acest caz, se poate ca descarcarea corona sa inceteze
datorita faptului ca intensitatea campului electric nu este
sufficient de mare pentru a intretine multiplicarea electronica.
Cand grosimea stratului de particule depuse
creste, ![]() devine superioara
tensiunii disruptive a gazului din patura, ceea ce duce la
strapungerea acestuia si la creerea unor mici "cratere". Gazul ionizat este
conductor iar canalele astfel formate diminueaza tensiunea disruptiva
intre electrozi ceea ce duce la aparitia arcului electric, cu distrugerea
locala a depunerii. Acest fenomen poarta numele de contra-emisie.
Randamentul de filtrare poate sa creasca prin antrenerea particulelor
depuse (formarea craterelor) si producerea de ioni de semn opus celor
produsi de descarcarea principala, diminuand astfel procesul de
incarcare a particulelor.
devine superioara
tensiunii disruptive a gazului din patura, ceea ce duce la
strapungerea acestuia si la creerea unor mici "cratere". Gazul ionizat este
conductor iar canalele astfel formate diminueaza tensiunea disruptiva
intre electrozi ceea ce duce la aparitia arcului electric, cu distrugerea
locala a depunerii. Acest fenomen poarta numele de contra-emisie.
Randamentul de filtrare poate sa creasca prin antrenerea particulelor
depuse (formarea craterelor) si producerea de ioni de semn opus celor
produsi de descarcarea principala, diminuand astfel procesul de
incarcare a particulelor.
Mentionam
si faptul ca rezistivitatea electrica a stratului de particule
depus variaza considerabil cu temperatura si umiditatea gazului.
Dupa Contal [6], daca
variatia este superioara unei rezistivitati critice de ![]() , depunerea devine ineficace.
, depunerea devine ineficace.
In anumite cazuri, zona operationala defavorabila se gaseste in gama temperaturii de functionare. Astfel, se va proceda la scaderea temperaturii fluidului portor, la cresterea continutului de apa in gaz sau la injectarea SO3, NH3, H2SO4, etc., care permit scaderea rezistivitatii [7].
4. Influenta concentratiei de particule asupra functionarii electrofiltrelor
O concentratie mare de particule poate avea consecinte negative asupra performantelor unui electrofiltru. Printre acestea, cele mai importante sunt modificarea repartitiei spatiale a campului electric si "inabusirea" descarcarii corona.
Atata timp cat particulele din interiorul precipitatorului se incarca cu sarcina electrica si de deplaseaza intre electrozii acestuia, ele participa la stabilirea unui curent electric. Cum mobilitatea acestor particule solide este de aproximatix 100 de ori mai mica decat a ionilor, crestrea concentratiei de particule are drept efect imediat creerea unei sarcini spatiale mai putin mobile in spatiul dintre electrozi. Fenomenul in cauza poate fi privit practic ca o diminuarea a mobilitatii ionilor :
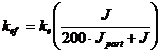 , (2)
, (2)
unde: J si Jpart sunt densitatile curentului ionic si respectiv celui particular, ke este mobilitatea ionilor in aer si kef mobilitatea echivalenta in prezenta particulelor.
Astfel, pentru aceeasi valoare a potentialului
electric aplicat electrozilor de ionizare, performantele de filtrare vor
fi mai reduse. Pentru a mentine un curent constant, este necesara
cresterea potentialului cu un ![]() [8,6]:
[8,6]:
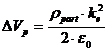 , (3)
, (3)
cu: ![]() - sarcina
spatiala particulara.
- sarcina
spatiala particulara.
Cat timp concentratia de particule in interiorul electrofiltrului este importanta, curentul de ionizare este scazut, conducand cateodata la stingerea descarcarii corona [6]. Mentinerea unui camp electric suficient de intens necesita o crestere a tensiunii. O concentratie ridicata poate favoriza strapungerea intre electrozi (riscurile unei explozii pot aparea cand concentratia de particule in aer are valori cuprinse intre 20 si 100 gm-3). Pentru concentratii mari, care contin un procent important de particule fine, exista un mare interes in divizarea electrofiltrului in mai multe parti separate una de cealalta, in functie de traiectoria gazului, parti ce au fiecare un camp electric distinct. Va fi astfel posibila utilizarea tensiunii si intensitatii adaptate concentratiei de particule depuse.
5. Efectul produs de reantrenarea particulelor
Reantrenarea particulelor colectate este de obicei asimilata fenomenului de erodare [9]. In cazul electrofiltrelor, se pot distinge cinci efecte importante:
interactiunea directa dintre fluxul de gaz si stratul de particule depus pe electrozi;
antrenarea particulelor, datorita curgerii gazului, in momentul in care acestea sunt inlaturate de pe suprafata electrozilor de depunere si cad datorita gravitatiei in buncarele situate in partea inferioara a electrofiltrului. Operatia de inlaturare a acestor particule se face in vederea evitarii 'colmatajului' (incarcarii peste limita) placilor colectoare si, de asemenea, pentru a limita fenomenul de contra-emisie ;
maturarea particulelor din cosul de depuneri din cauza unei distributii neadecvate a curgerii;
strapungerea electrica intre electrozi, ce poate provoca o "detasare" a unei parti din depunere;
contra-emisia, care altereaza depunerea si o fragilizeaza.
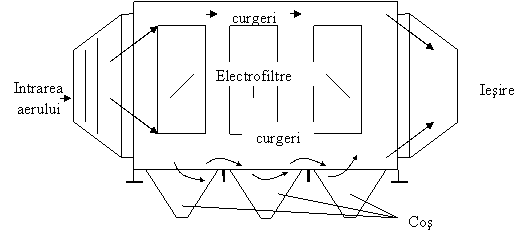
Figura 3. - Descrierea slabei alimentari a unui electrofiltru
Bump (1977)
Fenomenul de reantrenare este foarte complex si depinde de caracteristicile depunerii, deoarece particulele depozitate pe electrozii colectori sunt supuse fortelor Van der Waals si celor electrice datorita sarcinii lor reziduale. In functie de proprietatile lor dielectrice, particulele isi pierd mai repede sau mai incet sarcina electrica in contact cu electrozii colectori.
Masa volumica a particulelor joaca un rol important in decantarea si reantrenarea acestora in momentul lovirii electrozilor. Pentru particule cu densitatea mica este necesara o viteza a gazului cat mai redusa (0,5 m/s) pentru a evita reantrenarea, ceea ce limiteaza capacitatea electrofiltrului. Reantrenarea depinde in mod egal si de modul in care este conceput filtrul, de distributia curgerii gazoase, de modul in care sunt electrozii curatati si de forma geometrica a electrozilor.
In practica, reantrenarea poate provoca o diminuare in colectarea particulelor cu pana la 40-50%.
Pentru a diminua procesul de reantrenare, distributia gazului trebuie ameliorata prin utilizarea unor forme adecvate ale electrozilor si prin utilizarea mai multor sectiuni electrice. Reantrenarea este sensibila la curent si tensiune. Multe depuneri industriale au rezistivitati de ordinul 108 - 1010 Ωcm, valoare suficienta pentru a determina existanta unor forte de atractie importante. In aceste conditii, adeziunea depunerii este ameliorata mult de curentul ionic ce traverseaza patura atata timp cat acest curent este puternic si bine distribuit.
In numeroase cazuri, concentratia de particule in curgerea gazoasa este suficient de mare pentru a avea un efect asupra curgerii. Dupa Eaton [6], putem observa o atenuare a turbulentei pentru un procent de particule (masa particulelor divizata la masa gazului) mai mare de 10%. Aceasta atenuare este afectata de diferiti parametri cum ar fi numarul lui Stokes, numarul lui Reynolds si raportul intre diametrul particulelor si scara de lungime caracteristica a turbulentei.
Curgerile turbulente sunt descrise de ecuatia Reynolds si de ecuatiile de transport de energie cinetica turbulenta k si de imprastierea ε (acest model kε este adesea inclus in programele de simulare numerica, insa, el nu ofera decat posibilitatea modelarii turbulentei gazului la o scara foarte mica).
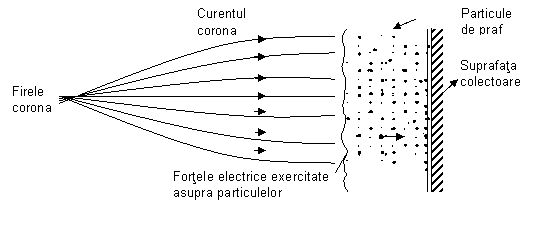
Figura 4. Schema fortelor electrice de adeziune asupra paturii de particule depuse
White
Modele de functionare a filtrelor electrostatice
Importanta dimensionarii corecte a unui electrofiltru, reprezinta pana la urma o problema economica, deoarece, intre gabaritul unui filtru si costul sau total de fabricatie exista o legǎtura foarte stransa. De-a lungul timpului, au fost elaborate modele teoretice capabile sa ofere informatii asupra randamentului de functionare a anumitor electrofiltre. In zilele noastre, dezvoltarea mijloacelor de calcul a permis aparitia modelelor numerice, bazate pe simularea fenomenelor produse in interiorul unui electrofiltru.
Randamentul de colectare a unui filtru electrostatic poate fi scris astfel:
![]() , (4)
, (4)
unde: Mf si Mi reprezinta masa totala a particulelor la intrarea si, respectiv iesirea din filtru.
Suspensia de gaz si particule reprezinta un sistem dispers. In general, in cazul precipitatoarelor electrostatice, particulele presupuse sferice sunt grupate in functie de dimensiunile lor in clase granulometrice si astfel se poate defini eficacitatea colectarii pentru diferite clase. De exemplu, pentru clasa i , eficacitatea colectarii este definita prin relatia:
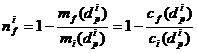 ,
,
unde mf(dpi) si mi(dpi) sunt masele particulelor din clasa granulometrica i la intrarea si iesirea din precipitator si cf(dpi) si ci(dpi) sunt concentratiile medii ale particulelor de clasa granulometrica i la intrarea si iesirea din precipitator.
Migrarea particulelor
In prezenta campului electric, particulele incarcate cu sarcina electrica sunt supuse in interiorul unui electrofiltru unei forte proportionale cu sarcina electrica; aceasta este forta lui Coulomb . Prezenta acestei forte are ca rezultat o miscare a particulelor catre placa colectoare, proces ce poarta denumirea de migrarea particulelor. Intr-o prima faza, ne-am propus caracterizarea acestui proces de migrare, in cazul simplu ce corespunde urmatoarelor ipoteze:
particulele sunt sferice, solide si nedeformabile; nu exista nici o interactiune intre ele;
particulele in miscare nu perturba curgerea de gaz;
curgerea de gaz este laminara si plana; astfel, componenta vitezei gazului pe directia perpendiculara placilor, este nula;
repartitia spatiala a campului electric din interiorul filtrului este uniforma.
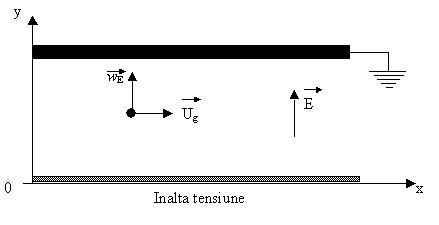
Figura 5. - Schema explicativa a
miscarii unei particule incarcate intre doua placi
paralele.
Fie o particula de diametru dp , de sarcina electrica qp si de viteza wE; ea se gaseste intr-o curgere de gaz de viteza Ug supusa unui camp electric presupus uniform si constant, E. Deplasarea acesteia in interiorul precipitatorului este data de relatia de echilibru mecanic:
![]() , (6)
, (6)
unde: mp reprezinta masa de particule, ![]() si
si ![]() sunt forta electrica
si forta de frecare date de expresiile urmatoare [7]:
sunt forta electrica
si forta de frecare date de expresiile urmatoare [7]:
![]() , (7)
, (7)
![]() , (8)
, (8)
cu : cf ( Re ) - coeficientul de frecare particula-gaz,
care depinde de numarul Reynolds,
Sp reprezinta aria
sectiunii unei particule, rg este densitatea gazului purtator
iar wE este viteza
relativa a particulei in raport cu cea a gazului. In cazul unui numar
Reynolds mic, dat de expresia [9] :
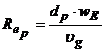 , (9)
, (9)
unde ng este vascozitatea cinematica a gazului., coeficientul de frecare are expresia urmatoare [7]:
![]() . (10)
. (10)
Aceasta situatie este tipica pentru precipitatoarele electrostatice industriale, in cazul unor particule ale caror diametre nu depasesc 20 mm.
In aceasta situatie, forta de frecare intre o particula sferica si gaz, este data prin relatia lui Stokes [7]:
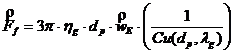 , (11)
, (11)
unde: hg este
vascozitatea dinamica a gazului si Cu factorul lui Cunningham
ce corecteaza expresia fortei de frecare vascoasa in
functie de marimea particulei considerate. Daca marimea
particulei atinge valoarea pentru care fluidul isi pierde caracterul de
mediu continuu (distanta medie intre molecule ![]() ), legea de miscare a lui Stokes trebuie corectata
cu factorul lui Cunningham (Cu) dat de
relatia [7]:
), legea de miscare a lui Stokes trebuie corectata
cu factorul lui Cunningham (Cu) dat de
relatia [7]:
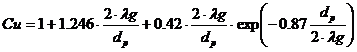 . (12)
. (12)
Figura 6 prezinta variatia factorului Cunningham in functie de diametrul particulelor in cazul aerului ambiant (lg mm). Inlocuind in relatia de echilibru mecanic expesia fiecarei forte, migrarea particulelor va fi caracterizata prin solutia ecuatiei diferentiale urmatoare:
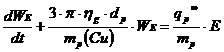 . (13)
. (13)
Viteza wE a unei particule pe directia normala a placilor este cunoscuta in literatura sub numele de viteza de migrare.
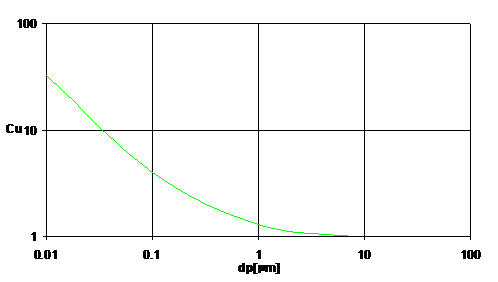
Figura 6. - Variatia factorului de corectie a lui Cunningham in functie de diametrele particulelor.
Daca consideram un moment initial t = 0, viteza wE a particulei este nula, iar solutia ecuatiei anterioare da evolutia urmatoare in timp:
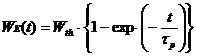 , (14)
, (14)
unde: Wth poarta denumirea de viteza teoretica de migrare [1,7,10] si are expresia urmatoare:
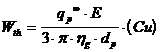 .
(15)
.
(15)
Timpul de relaxare a particulei considerate depinde de masa si talia particulei cat si de vascozitatea dinamica a gazului purtator:
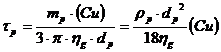 , (16)
, (16)
unde: mp este masa particulelor. Timpul p caracterizeaza comportamentul tranzitoriu al particulei pana in momentul in care aceasta se deplaseaza cu viteza constanta. Se remarca faptul ca timpul de relaxare este independent de conditiile electrice din interiorul filtrului.

Figura 7. - Variatia timpului de relaxare in functie de diametrele particulelor
( ng = 1,85 10-5 kg/ms si ρp = 2700 kg/m3 ).
Figura 7 prezinta variatia p in functie de diametrul particulelor. Se observa ca, pentru particulele fine (dp < 1m ) acest timp este foarte mic (p < 10s ).
Viteza de migrare teoretica poate fi considerata in acest caz, valoarea stationara a vitezei particulelor pe directia campului electric (perpendicular pe placile colectoare). Aceasta caracterizeaza procesul de migrare a particulelor in interiorul electrofiltrelor. Pe acest concept se bazeaza ansamblul de modele analitice.
Un studiu asupra vitezei teoretice de migrare necesita cunoasterea sarcinii electrice a particulelor, in functie de marimea lor. Pentru a arata variatia vitezei de migrare in functie de marimea unei particule, facem apel la o relatie simpla de calcul a sarcinii acumulate conform Cochet [11]. Aceasta relatie da sarcina limita prin camp (sarcina de saturatie) a unei particule care se gaseste intr-un camp electric de intensitate E:
 , (17)
, (17)
unde: e = ![]() este permitivitatea
vidului, iar er este constanta dielectrica a
particulelor considerata aici egala cu 4,5. Figura 8 reprezinta variatia sarcinii limita in
functie de diametrul particulelor la mai multe valori ale
intensitatii campului electric E.
este permitivitatea
vidului, iar er este constanta dielectrica a
particulelor considerata aici egala cu 4,5. Figura 8 reprezinta variatia sarcinii limita in
functie de diametrul particulelor la mai multe valori ale
intensitatii campului electric E.
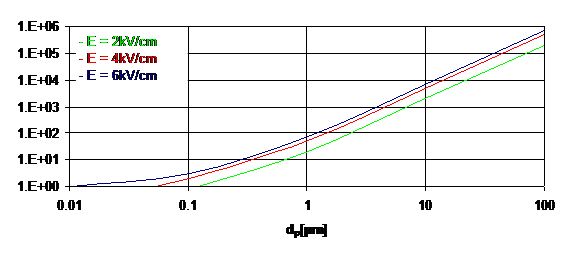
Figura 8. - Variatia sarcinii particulelor prezisa de Cochet in functie de diametrul dp
( λg = 0,065 μm si εr = 4,5 ).
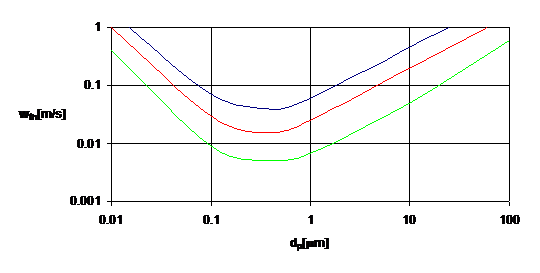
Figura 9. - Variatia vitezei de migrare teoretica wth in functie de marimea particulelor (λg = 0,065 μm si ηg = 1,85 10-5 kg/ms).
Utilizand rezultatele obtinute pentru sarcina electrica a particulelor aratate in Figura 8, s-a evaluat valoarea vitezei teoretice (Figura 9). S-a observat ca variatia vitezei in functie de diametrele particulelor are o valoare minima pentru particule cu diametrul egal cu 0,35 μm. O viteza mica de migrare diminueaza transportul de particule spre placile colectoare si, deci, eficacitatea colectarii. Putem anticipa aici o prima concluzie care rezulta din aceasta teorie simpla: in cazul filtrelor electrostatice, cele mai mici randamente de colectare sunt obtinute pentru particulele cuprinse intre 0,1 si 1 μm (Figura 9).
Modelul laminar
Acest model porneste de la ideea ca particulele dintr-un gaz aflate in suspensie prezinta toate aceeasi sarcina electrica; campul electric de precipitare este presupus uniform, fiind stabilit intre doua placi plane si paralele. Particulele se deplaseaza in directie axiala cu viteza medie a gazului si sunt supuse actiunii campului electric. Traiectoriile lor sunt deci linii drepte determinate de vitezele Ug si wth [1,7].
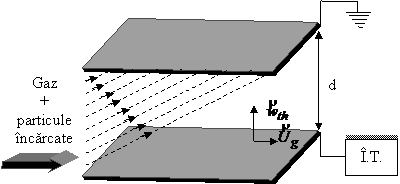
Figura 10. - Ilustrare schematica a modelului laminar.
O particula incarcata care intra in zona campului la o distanta d de placa colectoare va fi colectata dupa un timp t = d/wth; in acest timp, particulele ce se deplaseaza pe directia curgerii principale a gazului vor parcurge o anumita distanta LD.
![]() (18)
(18)
Astfel, toate particulele de aceasi marime, identic incarcate, vor fi colectate la o distanta egala sau mai mica decat LD. Eficacitatea fractionara nf a colectarii va putea fi calculata cu formula urmatoare:
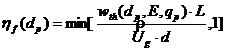 . (19)
. (19)
Conform acestui model, un precipitator electrostatic cu o lungime L va colecta toate particulele aflate in suspensie si va avea deci o eficienta de 100%. In cele ce urmeaza, vom vedea ca un precipitator dimensionat utilizand acest model, va avea in realitate o eficienta de colectare a particulelor mai mica, datorita curgerii turbulente a fluidului, ceea ce implica traiectorii de miscare ale particulelor mult mai complicate, pe de o parte, dar si o distributie neuniforma a campului electric, pe de alta parte.
Acest model este departe de realitate. Mai exista si conditiile electrice care pot fi foarte diferite decat cele impuse aici. Totusi, in cazul anumitor precipitatoare cu dublu etaj, acest model poate constitui punctul de plecare in studiul colectarii particulelor.
In precipitatoarele electrostatice industriale, curgerea gazului in spatiul interelectrodic este intotdeauna o curgere turbulenta. Turbulenta este data in parte de curgerea principala, dar mai ales se datoreaza fenomenului de vant ionic. Miscarea particulelor este in mare parte determinata de prezenta simultana a turbioanelor existente in curgerea de gaz si fortelor electrice care se exercita asupra lor. Astfel, traiectoriile particulelor sunt extrem de complicate si, in general, nu se pot determina prin expresii analitice simple.
In anul 1919, Anderson [10] remarca (in urma unei serii de experiente) ca procentul de particule necolectate (scapate din procesul de precipitare), descreste exponential cu valoarea lungimii precipitatorului. Trei ani mai tarziu, Deutsch [1], realizeaza o analiza teoretica in care argumenteaza aceasta comportare. In 1950, White [1] gaseste o formula identica cu aceea a lui Deutsch, bazata pe probabilitatea de colectare a particulelor de acelasi diametru (monodispersie).
In cazul modelului sau, Deutsch [1,2] considera existenta a doua zone:
zona de mijloc sau "inima" precipitatorului in care concentratia de particule este considerata uniforma in sectiunea transversala.Viteza medie a curgerii este considerata constanta.
o portiune de curgere laminara cu o grosime foarte mica, apropiata de placa colectoare (Figura 11);
Ipoteza existentei unei concentratii uniforme de particule in toata sectiunea transversala a filtrului este echivalent cu a considera unui amestec perfect a suspensiei gaz-particule. Acest lucru presupune de fapt o turbulenta de intensitate infinita in mijlocul precipitatorului. O particula poate fi colectata doar daca se afla in patura laminara situata aproape de fiecare placa colectoare, acolo unde forta lui Coulomb este cea dominanta.
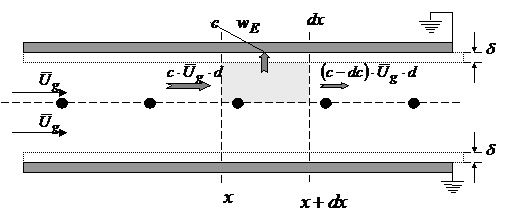
Figura 1 - Modelul Deutsch: reprezentare schematica a paturilor laminare si a bilantului masic al particulelor pe o lungime elementara dx.
In zona laminara campul electric este presupus uniform iar viteza particulelor pe directia perpendiculara placilor este presupusa constanta si are valoarea calculata prin expresia urmatoare:
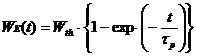 . (20)
. (20)
Consideram doua sectiuni transversale situate la o distanta dx una de alta, in directia curgerii de gaz.
In volumul ![]() unde h
reprezinta inaltimea placilor, se disting :
unde h
reprezinta inaltimea placilor, se disting :
![]() - fluxul de particule
care intra prin sectiunea situata pe abscisa x,
- fluxul de particule
care intra prin sectiunea situata pe abscisa x,
![]() - fluxul de particule
necolectate iesite prin sectiunea situata pe abscisa x + dx si
- fluxul de particule
necolectate iesite prin sectiunea situata pe abscisa x + dx si
![]() - fluxul particulelor
captate pe distanta dx.
- fluxul particulelor
captate pe distanta dx.
Se gaseste urmatoarea relatie:
![]() . (21)
. (21)
Integrand pe toata lungimea L a filtrului, se obtine dependenta dintre concentratia de particule la intrarea si iesirea din precipitator:
![]() , (22)
, (22)
expresie ce conduce la formula Deutsch-Anderson [1]:
![]() , (23)
, (23)
unde: S este suprafata totala a electrozilor colectori iar Dg este debitul volumic al gazului.
Chiar si in zilele noastre, acest model este utilizat ca prima etapa in calculele de dimensionare a noilor filtre.
Ipoteza modelului Deutsch, cea mai discutata, este aceea privind concentratia de particule care este presupusa constanta in sectiunea transversala a filtrului. Din anumite studii reiese ca aceasta este departe de a fi uniforma: structura curgerii gazului cat si fenomenul de electroforeza elimina particulele din zona centrala dirijandu-le catre placile colectoare. In general, viteza particulelor perpendiculare pe placa este considerata egala cu viteza de migrare teoretica exprimata prin relatia 23.
Acest model ignora toate fenomenele ce pot diminua randamentul colectarii, cum ar fi: reantrenarea particulelor colectate de fluxul gazos, influenta sarcinii libere de particule asupra descarcarii corona, etc.
In incercarea de a elimina unele din ipotezele modelului Deutsch, au fost elaborate alte modele mai complexe. Astfel s-a tinut seama si de influenta turbulentei fluxului gazos asupra transportului de particule, prin utlilizarea conceptului de difuzivitate turbulenta Dt.
Dupa cum s-a aratat, modelul Deutsch presupune concentratia de particule ca fiind uniforma in fiecare sectiune transversala a fluxului principal. Aceasta inseamna ca s-a considerat un coeficient de difuzivitate turbulenta de valoare infinita. O valoare finita Dt corespunde unui efect de difuzie care nu se opune decat partial efectului campului electric prezent intre electrozi; rezulta ca, concentratia de particule nu este uniforma pe directia perpendiculara peretilor ci ea creste de-a lungul planului median, spre peretii colectori.
Modelul Leonard porneste de la studiul influentei turbulentelor si considera ca punct de plecare ecuatia de conservare a masei de particule [12]:
![]() , (24)
, (24)
unde: c ( x,y,z ) - concentratia de particule.
Se considera axa Oz ca fiind perpendiculara pe placile colectoare (Figura 12).
Viteza
particulelor ![]() se poate scrie:
se poate scrie:
![]()
u + uE
![]() v + vE (25)
v + vE (25)
w + wE
unde: u, v, w sunt componentele vitezei gazului pe directiile Ox, Oy, Oz si uE, vE, wE reprezinta componentele vitezei particulelor incarcate sub efectul campului electric.
Din (24) si (25) rezulta
![]() . (26)
. (26)
Descompunand
viteza gazului si concentratia particulelor in parti
constante si variabile , ![]() si
si ![]() , se obtine:
, se obtine:
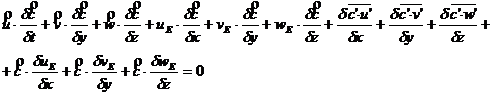 (27)
(27)
Se poate arata ca intre componentele fluctuante ale vitezei gazului si cele ale concentratiei de particule exista o legatura (particulele sunt antrenate de gaz si deci componenta fluctuanta a concentratiei c' depinde de componentele fluctuante ale vitezei gazului, respectiv u', v', w'). Rezulta deci ca ele nu sunt variabile independente. In general, in problemele in care intervine si turbulenta, intre corelatia care exista intre fluctuatia unei marimi scalare (concentratia, temperatura, etc.) si fluctuatiile vitezei unui fluid, se asociaza un efect mediu (in cazul acesta o concentratie medie [13]):
![]()
![]()
![]() , (28)
, (28)
unde: coeficientii Dtx , Dty, Dtz au dimensiunea unei constante de difuzie.
Chiar daca este vorba de un flux (de particule) rezultat dintr-o miscare de turbulenta a unui fluid, acesti coeficienti poarta denumirea de difuzivitate turbulenta. Introducandu-i in relatie, obtinem :
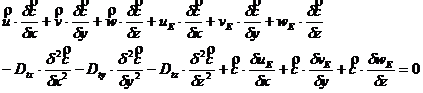 (29)
(29)
Autorii considera urmatoarele ipoteze de baza:
campul electric este considerat uniform;
curgerea gazului este considerata invarianta
doar pe directia Oy si ![]() ;
;
difuzivitatea turbulenta este
considerata uniforma si izotropa ( ![]() )
)
Neglijand influenta sarcinii spatiale a particulelor incarcate in camp electric, derivata vitezei wE in functie de z este nula [14]. In acest caz, ecuatia se reduce la
![]() . (30)
. (30)
Primii doi termeni reprezinta transportul de particule prin convectie si migrare iar ultimii doi termeni reprezinta transportul de particule asociat difuzivitatii turbulente.
In rezolvarea ecuatiei 30, intervine un parametru important Pe, numit numarul lui Peclet , cu expresia urmatoare [12]:
![]() . (31)
. (31)
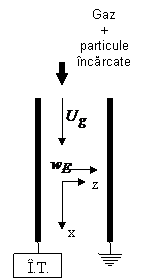
Figura 1 - Reprezentare schematica a problemei considerate de Leonard & co [12].
Acest numar masoara importanta
fortelor electrice asupra transportului de particule. Astfel, modelul Deutsch (![]() ) corespunde unui Pe
= 0 pe cand cazul laminar corespunde unui
) corespunde unui Pe
= 0 pe cand cazul laminar corespunde unui ![]() . Eficacitatea colectarii depinde de viteza de migrare a particulelor dar,
si de coeficientul de difuzie turbulenta. Teoria lui Deutsch, corespunzatoare cazului
. Eficacitatea colectarii depinde de viteza de migrare a particulelor dar,
si de coeficientul de difuzie turbulenta. Teoria lui Deutsch, corespunzatoare cazului ![]() , conduce la valori mai scazute ale
eficacitatii precipitatoarelor. Cu cat curgerea fluidului
este mai putin turbulenta, cu atat Pe creste, pana in cazul ideal cand
curgerea devine laminara
, conduce la valori mai scazute ale
eficacitatii precipitatoarelor. Cu cat curgerea fluidului
este mai putin turbulenta, cu atat Pe creste, pana in cazul ideal cand
curgerea devine laminara ![]() . Trebuie remarcat, de asemenea, ca pentru o valoare
finita a difuzivitatii turbulente, randamentul precipitatorului
este mai mare decat acela dat de teoria lui Deutsch (Figura 13).
. Trebuie remarcat, de asemenea, ca pentru o valoare
finita a difuzivitatii turbulente, randamentul precipitatorului
este mai mare decat acela dat de teoria lui Deutsch (Figura 13).
Un studiu interesant care foloseste modelul Leonard a fost realizat de Self & co [15,16]. Acesti autori
au folosit ecuatia de convectie-difuzie in cazul unui precipitator
fir-placa ce avea un camp electric neuniform. Au aratat ca, pentru
aceeasi valoare a intensitatii unui camp electric mediu format
pe pereti, eficacitatea colectarii este practic identica cu cea
obtinuta intr-un caz simplu de camp uniform. In calculele efectuate
de Self, valorile numarului Peclet electric considerate au fost
insa relativ mari ![]() .
.
In concluzie, metodele analitice elaborate de-a lungul mai multor decenii utilizeaza conceptul de viteza migrare a particulelor ca punct de plecare. Totusi , aceasta viteza este dificil de estimat, motiv pentru care rezultatele obtinute cu ajutorul acestor modele trebuie corectate in permanenta in practica prin coeficienti empirici. Un studiu detaliat asupra estimarii vitezei de migrare a fost realizat de Dumitran [17].
WeL/vd
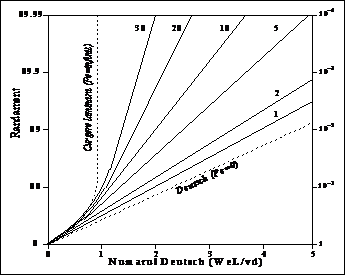
Figura 13. - Variatia randamentului in functie de numarul lui Deutsch.
5. Modelele numerice
Primele metode numerice au fost elaborate utilizand ecuatiile Deutsch pentru caracterizarea transportului particulelor in interiorul filtrelor. Viteza de migrare a fost calculata tinand cont de distributiile locale ale campului electric si de sarcina ionilor liberi determinate numeric. Cu viteza de migrare determinata, eficacitatea colectarii a fost calculata cu modelul Deutch pentru fiecare clasa granulometrica. Compararea cu rezultatele obtinute experimental asupra instalatiilor industriale a dus la necesitatea de a determina coeficienti de corectie pentru a tine seama de efectele care tind sa diminueze randamentul de separatie.
Alte modele numerice au fost elaborate in 1995,1997,1999 [4,17]. Toate acestea implica aceleasi componenete:
rezolvarea problemei electrice care permite aflarea distributiilor campului electric si a sarcinii ionilor liberi;
calculul marimilor mecanice care caracterizeaza curgerea de gaz tinand seama sau nu de efectul turbulentei;
determinarea traiectoriilor particulelor discrete sau calculul distributiei de concentratie a particulelor de diverse clase.
Pentru determinarea curgerii medii, curgerii secundare si intensitatii turbulentei, trebuie tinut seama de fortele electrice care se exercita asupra sarcinii spatiale formata de ioni si particule incarcate. In general, tehnica folosita consta in introducerea unei anumite surse de natura electrica in ecuatia Navier-Stokes. Din cauza complexitatii problemei, in majoritatea cazurilor se utilizeaza modele bidimensionale.
Distributia campului electric in prezenta unei sarcini libere este calculata pornind de la ecuatia Poisson.
Campul de viteze este obtinut pornind de la ecuatiile Navier-Stokes incluzand o sursa ce depinde de timp. Metodele numerice cum ar fi cele bazate pe diferente finite, pe elementele finite sau pe volume finite sunt utilizate pentru a ajunge la valori locale ale campului de viteze al gazului. Marimea turbulentei este estimata in general pornind de la modelele k-. Yamamoto [21,22] sau Yabe [23] care au simplificat problema de dinamica a gazului considerand doar ecuatia eliptica a vorticitatii.
Calculul sarcinii particulelor este esential pentru deducerea traiectoriilor acestora cat si pentru a estima eficacitatea colectarii. Exista mai multe modele care combina incarcarea prin camp cu cea prin difuzie. Cele mai utilizate sunt : Smith & McDonalds [24], McDonalds [25] si Lawless [26].
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5830
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved