Expresiile tensiunilor pentru starea plana

Starea plana de tensiuni se poate deduce din starea spatiala prin anularea parametrilor caracteristici uneia din directii. Pentru aprofundarea fenomenului se face in continuare un studiu independent al starii plane de tensiune. Dealtfel, in majoritatea cazurilor practice, unul din planele principale in punctul studiat poate fi indicat de la inceput; celelalte doua plane se determina din familia de plane perpendiculare pe primul, stabilirea orientarii acestora facandu-se in studiul starii plane.

Se considera un corp sub forma de placa de grosime constanta, solicitat in planul median zx. Se considera un punct M in interiorul corpului, iar in jurul acestuia o prisma triunghiulara elementara cu inaltimea de marimea grosimii. Sarcinile actioneaza in planul zx conform fig. (III.14).

Ca si in starea spatiala problema este de a determina tensiunile de pe o suprafata elementara dA_n in raport cu tensiunile de pe doua suprafete ortogonale dA_x si dA_z, cazul solicitarii in planul zx, fig. (III.15). Suprafetele elementare reprezinta ariile laterale ale prismei; suprafata dA_n facand unghiul a oarecare cu planul orizontal xy. Tensiunile s_n si t_n din starea spatiala se regasesc in tensiunile s_a si t_a, tensiuni dependente de unghiul a pentru o solicitare data.

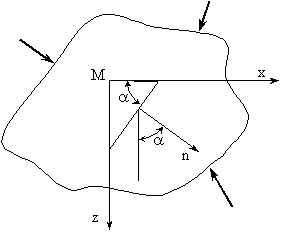
Fig. III.14 Planul de actiune al sarcinilor

Intre suprafetele laterale ale prismei exista relatiile:

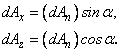(III.54)

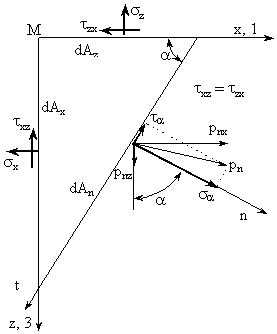
Fig. III.15 Suprafata elementara

Expresia tensiunii normale

Din conditia de echilibru dupa axa , fig. (III.15), rezulta:

. (III.55)

Inlocuind relatia (III.54) in (III.55) si simplificand prin dA_n rezulta:

. (III.56)

Se observa ca functiile trigonometrice ale unghiului a se pot transcrie pentru a nu avea produs de functii trigonometrice sub forma cosinusilor directori ai suprafetelor astfel:

, , m = 0 ( y) (III.57)

Punand conditia m = 0 in relatia (III.20), rezulta aceeasi expresie a tensiunii normale in starea plana, relatia (III.56):

. (III.58)

Studiul functiei tensiunii s_a se face mai usor pentru cazul in care functia trigonometrica se scrie functie de argumentul 2a. Rezulta:

, (III.59)

sau:

. (III.60)

Expresia tensiunii tangentiale

Din conditia de echilibru dupa axa , fig. (III.15), rezulta:

. (III.61)

Inlocuind relatia (III.54) in (III.61) si simplificand prin dA_n rezulta:

. (III.62)

Scriind relatia (III.62) pentru argumentul 2a, rezulta:

. (III.63)