Starea liniara de tensiune

Starea liniara de tensiune

Starea liniara de tensiune se caracterizeaza prin faptul ca, indiferent de orientarea sectiunii de calcul, tensiunile se dezvolta pe o aceeasi directie. Este caracteristica solicitarii axiale a barelor. Bara fiind solicitata dupa axa x, inseamna ca, oricare ar fi orientarea suprafetei de calcul p_n p_nx, axa x este pe directia principala 1. Planul ortogonal pe directia pe care se dezvolta tensiunile normale principale s are tensiunile tangentiale nule.

Starea liniara de tensiune se deduce simplu din starea plana prin anularea parametrilor caracteristici uneia din directii. Tratarea analitica prezentata in continuare se abordeaza pentru o intelegere mai usoara a solicitarilor simple.

Se considera o bara solicitata axial si un punct M in interiorul acesteia in jurul caruia se decupeaza o prisma triunghiulara, fig. (III.23).

Fig. III.23 Bara solicitata axial

Pentru starea liniara de tensiune, la fel ca si in celelalte stari studiate, problema este de a determina tensiunea (prin componentele sale si ) de pe o suprafata elementara dA_n oarecare, in raport cu tensiunea de pe o suprafata ortogonala pe directia solicitarii dA_x (avand in vedere orientarea solicitarii si a suprafetei, ). Pentru elementul studiat, fig. (III.24), relatiile intre caracteristicile geometrice sunt aceleasi ca in cazul plan.

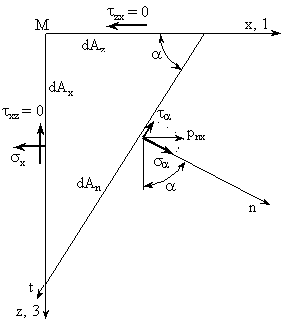
Fig. III.24 Suprafata elementara

Din conditia de echilibru dupa axa rezulta:

, (III.85)

. (III.86)

Aceasta relatie se obtine direct din starea:

spatiala, punand conditiile m = 0, s_z t_zx

plana, punand conditiile s_z t_zx

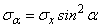
Din conditia de echilibru dupa axa rezulta:

, (III.87)

. (III.88)

Relatia se obtine direct din starea plana punand conditiile s_z t_zx

. (III.89)

Tensiunile principale se deduc anuland derivata expresiilor tensiunilor. In cazul tensiunilor normale:

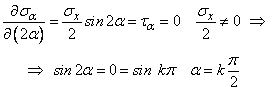(III.90)

Se observa ca si pentru starea liniara pe directia tensiunilor normale principale, tensiunile tangentiale sunt nule. Sintetizand cele prezentate, se poate scrie p_n = p_nx = s_x s s. In solicitarea axiala tensiunea normala se simbolizeaza simplu s fara indice.

Inlocuind valorile lui a deduse in expresia lui s_a (III.74), rezulta s si s

Se verifica invariantul tensiunilor normale:

Determinarea tensiunii tangentiale extreme se face prin anularea derivatei functiei tensiunii t_a

(III.91)

Inlocuind valorile lui a pentru directiile principale 6 si 6' in expresia lui t_a (III.88), rezulta t si t . Tensiunile normale pe aceste directii se determina prin folosirea relatiei (III.86):

Se verifica dualitatea tensiunilor tangentiale: .

Pentru redarea imaginii starii liniare de tensiune (planul zx) din jurul unui punct, se procedeaza astfel:

se reprezinta cubul elementar din jurul punctului M prin fata din planul zx;

se studiaza cazul pentru suprafetele orientate cu unghiurile si ;

la o scara mai mica se reprezinta elementul studiat pentru .

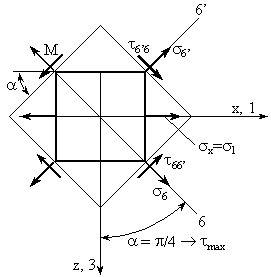
Fig. III.25 Starea liniara de tensiune

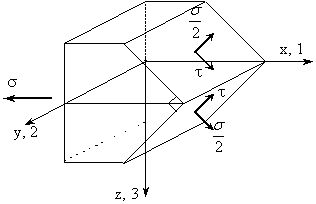
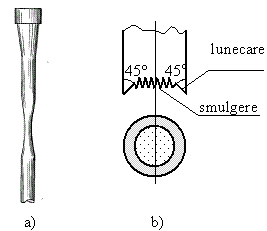
Fig. III.25 Starea liniara de tensiune