| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
Modele neliniare de alocare optima a resurselor in agricultura
Obiective : insusirea de catre studenti a metodelor de optimizare a consumului de resurse in
agricultura precum si elaborarea / rezolvarea modelelor de optimizare cu restrictii liniare si
functie-obiectiv patratica .
Cuprins
Productii si indicatori economici
Productii fizice si valorice
Indicatori economici ai productiei suplimentare
2 Optimele productiei suplimentare si aporturile factorilor
2.1 Optimele productiei suplimentare
2.2 Aporturile factorilor
3 Exemple
3.1 Doi factori si un produs
3.2 Un factor si doua produse
4 Modele cu restrictii liniare si functie-obiectiv patratica
4.1 Cazul cand toate restrictiile sunt ecuatii
4.2 Cazul cand toate restrictiile sunt inecuatii
Rezumat
6 Intrebari
7 Bibliografie
Cuvinte-cheie : optim marginal , de echilibru,economic,tehnic, maxim de venit cu cheltuieli
limitate , minim de cheltuieli cu venit garantat , rate ale substituirii factorilor , rate de
valorificare a unui factor prin produse diferite .
1 Productii,indicatori economici si aporturi
1.1 Productii fizice si valorice
Modelul neliniar care urmeaza , are ca scop alocarea optima a N factori variabili pentru M produse agricole.
Factorii constanti se cumuleaza separat in realizarea productiilor-martor ale produselor.
Exemple de factori variabili
a) La productia vegetala : densitatea plantelor, cantitatile de forta de munca,forta mecanizata,energie,ingrasaminte,apa de irigatie,etc.
b) La productia zootehnica : densitatea animalelor in spatiul de cazare ,cantitatile de forta de munca,forta mecanizata,energie,furaje, medicamente,etc.
Produsele vegetale sunt date de productiile fizice ale plantelor de pe suprafetele cultivate iar produsele animaliere sunt date de productiile raselor de animale si grupelor de animale cu efectivele existente.
Observam ca avem M.N factori nedistincti pentru M produse deoarece fiecare din cei N factori se aplica pentru fiecare din cele M produse in doze diferite.
Nivelul variabil al factorului J alocat pentru produsul I este de X(I,J)
unitati de factor J pe ha sau pe cap de animal (I=1,.,M; J=1,.,N) iar nivelul variabil al productiei fizice a produsului I este de Y(I) unitati de produs I pe ha sau pe cap de animal.
Legaturile celor M produse cu cei N factori sunt date de M functii de productie de tip polinomial-cubic , fiecare de cite N variabile :
![]()
Coeficientii Y0(I) , Y1(I,J) , Y2(I,J,K) , Y3(I,J) sunt dati pe baza datelor experimentale cu ajutorul programului de regresie cubica cu interactiuni COREGCUB .
Semnificatia acestor coeficienti este urmatoarea :
a) Y0(I) este productia-martor in untati de produs I pe ha sau pe cap de animal,realizata cu factorii constanti , fara cei N factori variabili .
b) Y1(I,J) este productia suplimentara in unitati de produs I pe ha sau pe cap de animal, datorata unitatii de factor variabil J .
c) Y2(I,J,K) este viteza de crestere a productiei suplimentare a produsului I cand
factorii variabili J si K cresc cu cate o unitate .
d) Y3(I,J) < 0 este acceleratia de scadere a productiei suplimentare a produsului I
cand factorul J creste cu o unitate.
Aceasta acceleratie negativa se datoreste limitei biologice a productie agrivole vegetale / animale in raport cu cresterea nivelului factorilor variabili , dupa principiul : in agricultura dublarea efortului nu atrage dupa sine dublarea efectului .
Pentru calculul cheltuielilor, venitului si profitului , sunt necesare urmatoarele date :
Cheltuielile constante CC(I) ale produsului I in lei pe ha sau pe cap de animal .
Aceste cheltuieli include toate cheltuielile productive(materiale si manopera) si neproductive
(taxe,impozite,TVA si cheltuieli neprevazute) cu factorii constanti , fara cheltuielile cu cei N factori variabili si fara cheltuielile cu recoltarea si transportul productiei vegetale / animale suplimentare a produsului I , realizata pe baza celor N factori variabili .
Costurile factorilor variabili CF(J) in lei pe unitate de factor J .
Aceste costuri acopera cumpararea,transportul si aplicarea la plante / animale a factorului variabil J .
Costurile recoltarii si transportului produselor CR(I) exprimate in lei pe unitatea de produs I .
Aceste costuri acopera recoltarea si transportul productiei-martor sau suplimentare a produsului I , realizata pe baza factorilor constanti respectiv acelor N factori variabili .
Preturile de vanzare ale produselor PV(I) in lei pe unitate de produs I .
Suprafetele in ha pentru culturi vegetale respectiv efectivele de animale domestice , notate S(I) , pe care se realizeaza produsul I .
1. Productii fizice
Y0(I) este productia-martor a produsului I in unitati de produs pe ha sau pe cap de animal , realizata numai cu factorii constanti , fara cei N factori variabili.
Daca macar unul din cei N factori variabili este esential pentru produsul I, atunci Y0(I) = 0 .
Acesta este cazul factorului variabil densitate plante / ha respectiv densitate animale in spatiul de cazare .
Notam cu YS(I,J) productia suplimentara a produsului I in unitati de produs pe ha sau pe cap de animal ,realizata pe baza factorului variabil J .
![]()
Avem relatiile :
Notam cu TYS(I) productia suplimentara a produsului I in unitati de produs pe ha sau pe cap de animal , realizata pe baza celor N factori variabili . Avem relatiile :
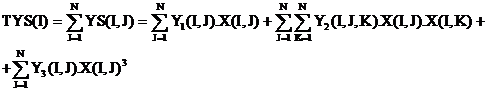
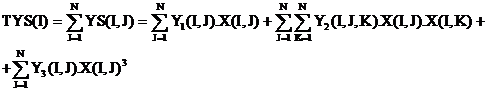
Partea din TYS(I) in care apare X(I,J) este :
Cantitatea Y(I) = Y0(I) + TYS(I) este productia produsului I in unitati de produs pe ha sau pe cap de animal in raport cu toti factorii constanti sau variabili .
Pentru toate suprafetele / efectivele de animale , notate cu S(I) , productia-martor a produsului I , realizata pe baza factorilor constanti este SY0(I) = Y0(I).S(I) , productia suplimentara a produsului I , realizata pe baza celor N factori variabili , este SYS(I) = TYS(I).S(I) adica :
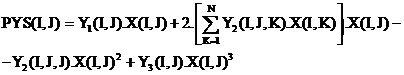
si productia totala a produsului I , realizata pe baza factorilor constanti si variabili , este
SY(I) = SY0(I)+SYS(I)=Y(I).S(I)
2. Venituri
V0(I) = PV(I).Y0(I) este venitul-martor al produsului I in lei pe ha sau pe cap de animal , realizat pe baza factorilor constanti , fara cei N factori variabili.
VS(I,J) = PV(I).YS(I,J) este venitul suplimentar al produsului I in lei pe ha sau pe cap de animal , realizat prin utilizarea factorului variabil J .
Notam cu TVS(I) venitul suplimentar al produsului I , realizat prin utilizarea celor N factori variabili .
![]()
Avem relatiile :
Partea din TVS(I) in care apare X(I,J) este PVS(I)=PV(I).PYS(I)
![]()
Pentru toate suprafetele /
efectivele de animale , notate cu S(I) ,
venitul-martor pentru toate produsele , realizat pe baza factorilor
constanti , este :
![]()
Venitul suplimentar pentru toate
produsele , realizat pe baza celor N factori variabili , este :
iar venitul total pentru toate produsele , realizat pe baza tuturor factorilor constanti si variabili , este SV=SV0 + SVS
Cheltuieli
C0(I) = CC(I) + CR(I).Y0(I) sunt cheltuielile-martor pentru produsul I , in lei pe ha sau pe cap de animal , necesare pentru utilizarea factorilor constanti , fara cei N factori variabili .
Notam cu CS(I,J) cheltuielile suplimentare pentru produsul I , in lei pe ha sau pe cap de animal , necesare pentru utilizarea factorului J .
Avem relatiile : CS(I,J) = CR(I).YS(I,J)+CF(J).X(I,J)
Notam cu TCS(I) cheltuielile suplimentare pentru produsul I , in lei pe ha sau pe cap de animal , necesare pentru utilizarea celor N factori variabili.
![]()
Avem relatiile :
Partea din TCS(I) in care apare X(I,J) este :
PCS(I)=CR(I).PVS(I,J) + CF(J).X(I,J)
![]()
Pentru toate suprafetele /
efectivele de animale , notate cu S(I) ,
cheltuielile-martor pentru toate produsele , necesare pentru utilizarea
factorilor constanti , sunt :
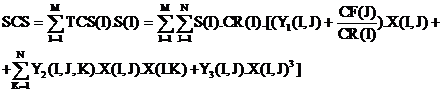
, cheltuielile suplimentare pentru
toate produsele , necesare pentru utilizarea celor N factori variabili , sunt :
iar cheltuielile totale pentru toate produsele , necesare pentru utilizarea tuturor factorilor constanti si variabili , sunt SC = SC0 + SCS
Marimile SC0 , SCS , SC se exprima in lei .
4. Profituri
P0(I) = V0(I) - C0(I) = [PV(I) - CR(I)].Y0(I) - CC(I) este profitul-martor al produsului I in lei pe ha sau pe cap de animal , realizat pe baza utilizarii factorilor constanti , fara cei N factori variabili .
Notam cu PS(I,J) profitul suplimentar al produsului I in lei pe ha sau pe cap de animal , realizat prin utilizarea factorului variabil J .
Avem relatiile :
PS(I,J) = VS(I,J) - CS(I,J) = [PV(I) - CR(I)].YS(I,J) - CF(J).X(I,J)
![]()
Notam cu TPS(I) profitul suplimentar al produsului I in lei pe ha sau pe cap de
animal , realizat prin utilizarea celor N factori variabili .
Partea din TPS(I) in care apare X(I,J) este :
PPS(I,J) = PVS(I,J) - PCS(I,J) = [PV(I) - CR(I)].PYS(I) - CF(J).X(I,J)
Pentru toate suprafetele / efectivele de animale , notate cu S(I), profitul-martor pentru toate produsele , realizate pe baza factorilor constanti , este :
![]()
, profitul suplimentar pentru toate produsele , realizat pe baza celor N factori variabili , este :
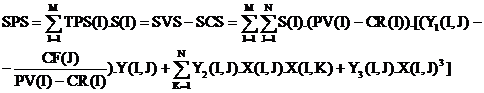
iar profitul total pentru toate produsele , realizat pe baza tuturor factorilor
constanti si variabili , este SP = SP0 + SPS
Ratele profitului
RP0(I) = P0(I) / C0(I) este rata profitului-martor pentru produsul I , realizata pe baza factorilor constanti , fara cei N factori variabili . Avem :
![]()
RPS(I,J) = PS(I,J) / CS(I,J) este rata profitului suplimentar pentru produsul I , realizata pe baza factorului variabil J . Avem relatiile :
![]()
adica :
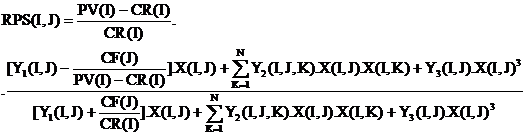
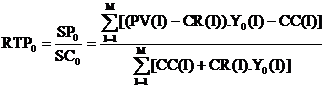
Rata profitului-martor pentru
toate produsele , realizata pe baza factorilor constanti , fara
cei N factori variabili , este :
RTPS = SPS / SCS este rata profitului suplimentar pentru toate produsele , realizata pe baza celor N factori variabili .
RTP = SP / SC este rata profitului pentru toate produsele , realizata pe baza factorilor constanti si a celor N factori variabili .
1.2 Indicatori economici ai productiei suplimentare
6. Indicatori intre produse si factori variabili
A. Indicatori medii ai produsului I in raport cu factorul variabil J
![]()
Productia medie este YM(I,J) = PYS(I,J) / X(I,J) adica :
Venitul mediu este VM(I,J) = PVS(I,J) / X(I,J) adica VM(I,J) = PV(I).YM(I,J)
Cheltuielile medii sunt : CM(I,J) = PCS(I,J) / X(I,J) adica CM(I,J) = = CR(I).YM(I,J) + CF(J)
Profitul mediu este PM(I,J) = PPS(I,J) / X(I,J) adica PM(I,J) = [PV(I) - CR(I)].YM(I,J) - CF(J)
Acesti indicatori prezinta productia / venitul / cheltuielile / profitul suplimentar al produsului I care corespunde unitatii factorului variabil J .
B. Indicatori marginali ai produsului I in raport cu factorul variabil J
![]()
Productia marginala este
derivata partiala YD(I,J) =
∂ PYS(I,J) / ∂ X(I,J) adica :
Venitul marginal este derivata partiala CD(I,J) = ∂ PVS(I,J) / ∂ X(I,J) adica:CD(I,J) = CR(I).YD(I,J)+CF(J)
Profitul marginal este derivata partiala PD(I,J) = ∂ PPS(I,J) / ∂ X(I,J) adica: PD(I,J) = [PV(I) - CR(I)].YD(I,J) - CF(J)
Acesti indicatori reprezinta variatia productiei / venitului / cheltuielilor / profitului suplimentar
din produsul I , provocata de variatia factorului variabil J cu o unitate .
C. Indicatori de elasticitate ai produsului I in raport cu factorul variabil J
Elasticitatea productiei este EY(I,J) = YD(I,J) / YM(I,J)
Elasticitatea venitului este EV(I,J) = VD(I,J) / VM(I,J) adica EV(I,J) = EY(I,J)
![]()
Elasticitatea cheltuielilor este
EC(I,J) = CD(I,J) / CM(I,J) adica :
![]()
Elasticitatea profitului este :
EP(I,J) = PD(I,J) / PM(I,J) adica :
Acesti indicatori reprezinta variatia procentuala a productiei / venitului / cheltuielilor / profitului suplimentar al produsului I , provocata de variatia factorului variabil J cu 1 % .
7. Indicatori intre profit si cheltuieli
D. Rata medie a profitului din produsul I in raport cu factorul variabil J
![]()
Este RM(I,J) = PPS(I,J) / PCS(I,J) =
PM(I,J) / CM(I,J) adica :
Acest indicator reprezinta profitul suplimentar in lei din produsul I ,realizat pe baza factorului variabil J , ce corespunde la un leu cheltuit de produsul I in raport cu factorul variabil J .
E. Rata marginala a profitului din produsul I in raport cu factorul variabil J
![]()
Este RD(I,J) = ∂ PPS(I,J)
/ ∂ PCS(I,J) = PD(I,J) /
CD(I,J) adica :
Acest indicator reprezinta variatia profitului suplimentar din produsul I in raport cu factorul variabil J , provocata de variatia cu un leu a cheltuielilor suplimentare ale produsului I in raport cu facctorul variabil J .
F. Elasticitatea ratei profitului din produsul I in raport cu factorul variabil J
Este ER(I,J) = RD(I,J) / RM(I,J) adica :
![]()
Acest indicator reprezinta
variatia procentuala a profitului suplimentar din produsul I in
raport cu factorul variabil J , provocata de variatia cu 1 % a cheltuielilor suplimentare ale
produsului I in raport cu factorul variabil J .
8. Indicatori de substituire a factorilor
G. Rata medie a substituirii factorului variabil J cu factorul variabil K
Este RMS(I,J,K) = PM(I,J) / PM(I,K)
Acest indicator reprezinta cantitatea de unitati de factor variabil K care corespunde unei unitati de factor J , in realizarea aceluiasi profit suplimentar din produsul I .
H. Rata marginala a substituirii factorului variabil J cu factorul variabil K
Este RDS(I,J,K) = PD(I,J) / PD(I,K)
Acest indicator reprezinta cantitatea de unitati cu care trebuie sa creasca doza de factor variabil K , daca doza de factor variabil J creste cu o unitate , astfel ca profitul suplimentar din produsul I sa creasca cu aceeasi suma .
I. Elasticitatea ratei substituirii factorului variabil J cu factorul variabil K
Este ERS(I,J,K) = RDS(I,J) / RDS(I,K)
Acest indicator reprezinta procentele cu care trebuie sa creasca doza de factor variabil K , daca doza de factor variabil J creste cu 1 % , astfel ca profitul suplimentar din produsul I sa creasca cu acelasi procent .
Indicatori de valorificare a factorilor prin produse
Este RMV(I,H,K) = PM(I,K) / PM(H,K)
Acest indicator reprezinta numarul de unitati ale produsului H care corespunde la o unitate de produs I , care dau acelati profit din utilizarea factorului variabil K .
Este RMV(I,H,K) = PM(I,K) / PM(H,K)
Acest indicator reprezinta numarul de unitati cu care trebuie sa creasca produsul H atunci cand produsul I creste cu o unitate , astfel ca profitul suplimentar din utilizarea factorului variabil K sa creasca cu aceeasi suma.
Este ERV(I,H,K) = RDV(I,H,K) / RMV(I,H,K)
Acest indicator reprezinta numarul de procente cu care trebuie sa creasca produsul H atunci cand produsul I creste cu 1 % , astfel ca profitul suplimentar din utilizarea factorului variabil K sa creasca cu acelasi procent.
2 Optimele productiei suplimentare si aporturi
2.1 Optimele productiei suplimentare
I . OPTIMUL MARGINAL
In acest caz avem productia suplimentara marginala YD(I,J) = maxim deci avem derivatele partiale
nule ∂ YD(I,J) / ∂ X(I,J) = 0 adica : 2.Y2(I,J,J) + 6.Y3(I,J).X(I,J) = 0 cu solutia :
XD(I,J) = [Y2(I,J,J) / ( - 3.Y3(I,J)]
Acestea sunt dozele optime ale alocarii factorului variabil J pentru produsul I , pentru care YD(I,J) = maxim .
In acest caz sunt maxime VD(I,J) , CD(I,J) , PD(I,J) conform relatiilor din sectiunea 2.1 B.
Este deasemenea maxima RD(I,J) conform relatiilor de la punctul 1.2 E.
II . OPTIMUL DE ECHILIBRU
In acest caz avem productia suplimentara medie YM(I,J) = maxima deci avem derivatele partiale nule ∂ YM(I,J) / ∂ X(I,J) = 0 adica : Y2(I,J,J) + 2.Y3(I,J).X(I,J) = 0 cu solutia :
XM(I,J) = [Y2(I,J,J)] / [ - 2.Y3(I,J)]
adica dozele optime ale alocarii factorului variabil J pentru produsul I pentru care YM(I,J) = maxima .
In acest caz sunt maxime VM(I,J) , CM(I,J) , PM(I,J) conform relatiilor din sectiunea 2.1 A.
Daca egalam marimea YM(I,J) de la punctul 1 A. cu marimea YD(I,J) de la punctul 2.1 B. gasim :
- Y2(I,J,J).X(I,J) = 2.Y3(I,J).X(I,J) deci :
X(I,J) = [Y2(I,J,J)] / [ - 2.Y3(I,J)] adica exact valorile din relatia (2) .
Rezulta ca pentru dozele de echilibru din relatia (2) avem :
YM(I,J) = maxim = YD(I,J) asa ca EY(I,J) = 1
Din relatiile de la punctele 1.1 A. si 1.1 B. rezulta ca pentru dozele de echilibru din relatia (2) avem :
VM(I,J) = maxim = VD(I,J) asa ca EV(I,J) = 1 ;
CM(I,J) = maxim = CD(I,J) asa ca EC(I,J) = 1 ;
PM(I,J) = maxim = PD(I,J) asa ca EP(I,J) = 1 .
Aceasta situatie justifica denumirea optimului de echilibru :
O crestere a factorului variabil J cu 1 % atrage dupa sine o crestere a productiei / venitului / cheltuielilor / profitului suplimentar din produsul I , datorata factorului variabil J , tot cu 1 % ( egalitate intre cresterea procentuala de efort fizic si cresterea procentuala de efect financiar).
De la punctul 1.2 D. avem :
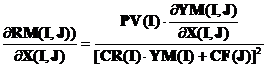
deci daca ∂ YM(I,J) /
∂ X(I,J) = 0 adica daca profitul mediu YM(I,J) = maxim atunci ∂ RM(I,J) / ∂ X(I,J) = 0 deci atunci rata medie a
profitului RM(I,J) = maxima .
Din relatiile de la punctele 1.2 D. s 1.2 E. rezulta ca relatia YM(I,J) = maxim=YD(I,J) implica RM(I,J) = maxim=RD(I,J) deci ER(I,J) = 1 .
In cuvinte , la optimul de echilibru , o crestere cu 1 % a cheltuielilor cu factorul variabil J , fata de valoarea existenta a acestor cheltuieli , atrage dupa sine o crestere a profitului suplimentar al produsului I , datorata factorului variabil J , tot cu 1 % ( egalitate intre cresterea procentuala de efort financiar si cresterea procentuala de efect financiar).
III . OPTIMUL ECONOMIC
![]()
In acest caz avem profitul
suplimentar total SPS = maxim deci avem
derivatele partiale nule ∂
SPS(I,J) / ∂ X(I,J) = 0 adica PD(I,J) =0 sau : [PV(I) - CR(I)].YD(I,J) - CF(J) =0 de unde obtinem
relatiile (3) :
(I=1,.,M ; J=1,.,N)
Relatiile (3) constituie M sisteme patratice de N ecuatii cu N necunoscute X(I,J) .
Aceste sisteme patratice se rezolva cu programul SISPAT dand solutiile XE(I,J) .
Pentru dozele de optim economic XE(I,J) avem si EP(I,J) = 0 conform relatiilor 2.1 C. , precum si RD(I,J) = 0 conform relatiilor 1.2 D.
IV . OPTIMUL TEHNIC
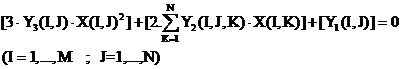
In acest caz avem productiile fizice suplimentare SYS(I) = maxime deci avem derivatele partiale nule ∂ SYS(I) / ∂ X(I,J) = 0 adica YD(I,J) =0 de unde obtinem relatiile (4) :
Relatiile (4) constituie M sisteme patratice de N ecuatii cu N necunoscute X(I,J).
Aceste sisteme patratice se rezolva cu programul SISPAT dand solutiile XT(I,J) .
![]()
Venitul suplimentar pentru toate
produsele este dat de relatia :
deci daca SYS(I) =maxime , rezulta SVS = maxim pentru dozele XT(I,J) .
Pentru dozele de optim tehnic XT(I,J) , din relatiile de la punctele 1.1 B. si 1.1 C. rezulta VD(I,J)=0 , CD(I,J)= - CF(J) respectiv EY(I,J)=EV(I,J)=0 .
Din relatia de la punctul 1.1 B. , pentru YD(I,J) = 0 rezulta PD(I,J)= - CF(J) iar din relatia de la punctul 1.2 E. rezulta RD(I,J)= - 1 .
In intervalele [XT(I,J) ; +∞) exista valorile X(I,J) care anuleaza profitul suplimentar
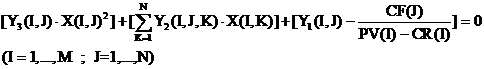
total : SPS = 0 ceace se realizeaza daca au loc relatiile
(5) :
Relatiile (6) constituie M sisteme patratice de N ecuatii cu N necunoscute care se rezolva cu programul SISPAT dand solutiile XR(I,J) .
V . OPTIMUL DE VENIT CONDITIONAT DE CHELTUIELI
In acest caz avem venitul suplimentar din toate produsele : SVS=maxim conditionat de limitarea cheltuielilor suplimentare pentru toate produsele : SCS=SC0 ( limita de cheltuieli ).
Cum SPS=SVS - SCS = SVS - SC0 , daca SVS=maxim conditionat rezulta SPS=maxim conditionat ; deasemenea rata profitului suplimentar pentru toate produsele RPS=SPS / SCS = SPS / SC0 =maxim conditionat odata cu SPS .
Functia Lagrange a optimului condtionat de mai sus , are forma :
L = SVS - LV.(SCS - SC0) unde LV este multiplicatorul Lagrange .
Avem conditiile necesare de optim:
∂ L / ∂ X(I,J) =0 (I=1,.,M , J=1,.,N)
SCS=SC0
adica :
VD(I,J) - LV. CD(I,J) = 0
SCS=SC0
de unde rezulta :
[PV(I) - LV.CR(I)].YD(I,J) - LV.CF(J)=0
SCS=SC0
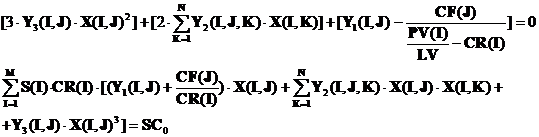
deci obtinem relatiile (6) :
Pentru fiecare valoare a multiplicatorului Lagrange LV ≥ 1 , relatiile (6) constituie un sistem patratic de MN ecuatii cu MN necunoscute X(I,J) care se rezolva cu programul SISPAT dand solutiile XC(I,J) .
Interpretarea multiplicatorului Lagrange LV : avem LV = VD(I,J) / CD(I,J) adica LV este egal cu cresterea de venit suplimentar al produsului I din factorul variabil J , cand cresterea cheltuielilor suplimentare ale produsului I din factorul variabil J peste valoarea limita SC0, este de o unitate monetara.
Avem RD(I,J) = LV - 1 pentru orice I=1,.,M si orice J=1,.,N .
Pentru LV=1 avem optim economic iar pentru LV=0 avem optim tehnic.
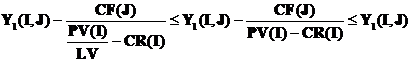
Deoarece LV≥ 0 avem :
VI . OPTIMUL DE CHELTUIELI CONDITIONAT DE VENIT
In acest caz avem cheltuielile suplimentare pentru toate produsele : SCS=minim , conditionate de garantarea venitului suplimentar pentru toate produsele : SVS=SV0 ( garantie de venit ).
Cum SPS=SVS - SCS = SV0 - SCS , daca SCS=minim conditionat rezulta SPS=maxim conditionat ; deasemenea rata profitului suplimentar pentru toate produsele RPS=SPS / SCS = maxim conditionat caci SPS=maxim conditionat si SCS=minim conditionat .
Functia Lagrange a optimului conditionat de mai sus , are forma :
L = SCS - LC.(SVS - SV0) unde LC este multiplicatorul Lagrange .
Avem conditiile necesare de optim:
∂ L / ∂ X(I,J) =0 (I=1,.,M , J=1,.,N)
SVS=SV0
adica :
CD(I,J) - LC.VD(I,J) = 0
SVS=SV0
de unde rezulta :
[CR(I) - LC.PV(I)].YD(I,J) -CF(J)=0
SVS=SV0
deci obtinem relatiile (7) :
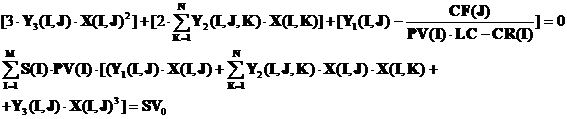
Pentru fiecare valoare a multiplicatorului Lagrange LC ≤ 1 , relatiile (7) constituie un sistem patratic de MN ecuatii cu MN necunoscute X(I,J) care se rezolva cu programul SISPAT dand solutiile XV(I,J) .
Interpretarea multiplicatorului Lagrange LC : avem LC = CD(I,J) / VD(I,J) adica LC este egal cu cresterea de cheltuieli suplimentare ale produsului I , din factorul variabil J , cand cresterea venitului suplimentar al produsului I , din factorul variabil J peste valoarea garantata SV0 , este de o unitate monetara.
Avem RD(I,J) = (1 / LC )- 1 pentru orice I=1,.,M si orice J=1,.,N .
Pentru LC=1 avem optim economic iar pentru LC=∞ avem optim tehnic.
Deoarece LV ≤ 1 avem :
![]()
Optimele de la punctele 2.1-2.6 si ratele medie si marginala ale profitului oricarui produs in raport cu orice factor , se prezinta grafic astfel :
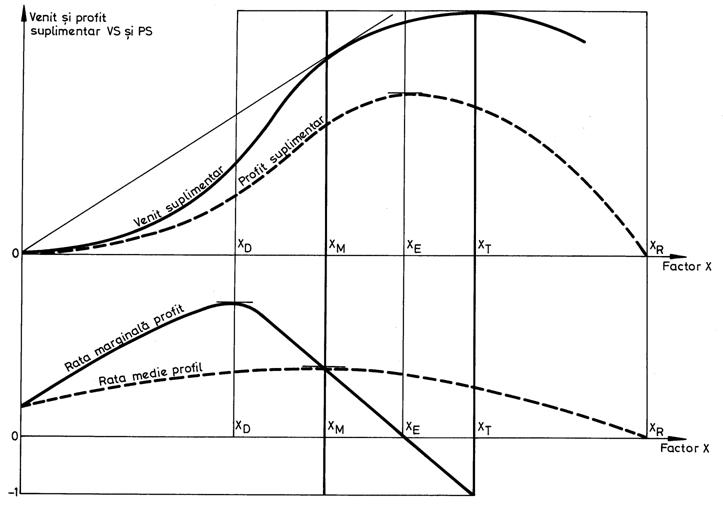
In acest desen apar in mod clar urmatoarele intervale de valori ale factorului :
I. Intervalul de crestere accelerata [0 ; XD] in care venitul ,profitul,rata medie si cea marginala a profitului cresc iar rata marginala a profitului este mai mare ca rata medie a profitului (elasticitatea ratei profitului este > 1).
II. Intervalul de crestere incetinita [XD ; XM] in care venitul ,profitul,rata medie a profitului cresc ,rata marginala a profitului scade iar rata marginala a profitului este mai mare ca rata medie a profitului (elasticitatea ratei profitului este > 1).
III. Intervalul de crestere saturata [XM ; XE] in care venitul ,profitul cresc ,rata medie si cea marginala a profitului scad iar rata marginala a profitului este mai mica ca rata medie a profitului (elasticitatea ratei profitului este cuprinsa intre 0 si 1).
IV. Intervalul de declin economic [XE ; XT] in care venitul creste ,profitul,rata medie si cea marginala scad iar rata marginala a profitului este negativa si mai mare ca - 1 (elasticitatea ratei profitului este < 0).
V. Intervalul de declin tehnico-economic [XT ; XR] in care venitul , profitul,rata medie si cea marginala scad iar rata marginala a profitului este negativa si mai mica ca
- 1 (elasticitatea ratei profitului este < 0).
VI. Intervalul de faliment economic [XR ; +∞] in care profitul este negativ .
2.2 Aporturi
A. APORTURI PENTRU PRODUCTII
Daca X I[0,X0] este un factor variabil iar Y=Y0+f(x) este un produs cu valoarea martor Y0 , valoarea medie a lui Y este data de relatia (7) :
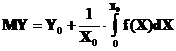
Fie XO(I,J) doza curenta a factorului variabil J , alocat produsului I si fie Y(I) nivelul
variabil al productiei fizice a
produsului I pe ha
sau pe cap de animal.
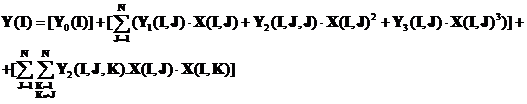
Avem :
Conform formulei (7) valoarea medie a productiei fizice a produsului I pe intervalul [0;XO(I,J)] va fi :
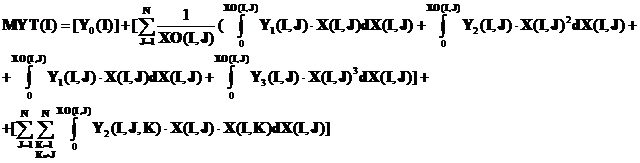
adica relatia (8) :
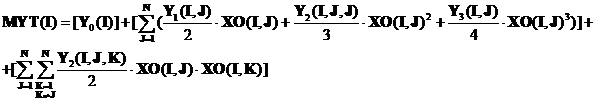
a) Valoarea medie martor a produsului I datorata factorilor constanti este :
MYO(I) = Y0(I)
b) Valoarea medie a produsului I , datorata factorilor variabili , este :
![]()
c) Valoarea medie a produsului I , datorata interactiunii factorilor variabili,este:
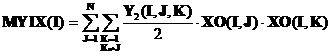
Relatia (8) devine : MYT(I)=MYO(I)+MYX(I)+MYIX(I)
Aporturile in procente ale factorilor constanti si variabili la productia fizica a produsului I sunt :
d) Aportul factorilor constanti : AYO(I) = MYO(I) / MYT(I)
e) Aportul factorilor variabili : AYX(I) = MYX(I) / MYT(I)
f) Aportul interactiunilor factorilor variabili :
AYIX(I) = MYIX(I) / MYT(I) = 1 - AYO(I) - AYX(I)
B. APORTURI PENTRU VENIT
Printr-un calcul similar cu cel de la punctul 2.2.A , gasim valorile medii :
a) MVO(I) = PV(I).MYO(I) si pentru toate produsele :
![]()
b) MVX(I) = PV(I).MYX(I) si pentru toate produsele :
![]()
c) MVIX(I) = PV(I).MYIX(I) si pentru toate produsele :
![]()
d) MVT(I) = PV(I).MYT(I) si pentru toate produsele :
![]()
Avem relatia : MVTT=MVTO+MVXT+MVIXT
Aporturile in procente ale factorilor constanti si variabili la venitul din toate produsele, sunt :
e) Aportul factorilor constanti : AVO(I) = MVO(I) / MVT(I)
f) Aportul factorilor variabili : AVX(I) = MVX(I) / MVT(I)
g) Aportul interactiunilor factorilor variabili :
AVIX(I) = MVIX(I) / MVT(I) = 1 - AVO(I) - AVX(I)
C. APORTURI PENTRU CHELTUIELI
Printr-un calcul similar cu cel de la punctul 2.2.A , gasim valorile medii :
MCO(I) = C0 (I)=CC(I)+CR(I).Y0(I) si pentru toate produsele :
![]()
h) MCX(I) = CR(I).MYX(I)+(CF(J) / 2).XO(I,J) si pentru toate produsele :
![]()
i) MCIX(I) = CR(I).MYIX(I) si pentru toate produsele :
j) ![]()
MCT(I) = MCO(I)+MCX(I)+MCIX(I) si pentru toate produsele :
![]()
Avem relatia : MCTT=MCTO+MCXT+MCIXT
Aporturile in procente ale factorilor constanti si variabili la venitul din toate produsele, sunt :
e) Aportul factorilor constanti : ACO(I) = MCO(I) / MCT(I)
f) Aportul factorilor variabili : ACX(I) = MCX(I) / MCT(I)
g) Aportul interactiunilor factorilor variabili :
ACIX(I) = MCIX(I) / MCT(I) = 1 - ACO(I) - ACX(I)
D. APORTURI PENTRU PROFIT
![]()
Printr-un calcul similar cu cel de la punctul 2.2 A , gasim valorile medii :
a) MPO(I) = P0(I)=[PV(I) - CR(I)].Y0(I) - CC(I) si pentru toate produsele :
![]()
k) MPX(I) =[PV(I) - CR(I)].MYX(I) - (CF(J) / 2 ).XO(I,J) si pentru toate produsele :
![]()
l) MPIX(I) = [PV(I) - CR(I)].MYIX(I) si pentru toate produsele :
![]()
m) MVT(I) = PV(I).MYT(I) si pentru toate produsele :
![]()
Avem relatia : MPTT=MPTO+MPXT+MPIXT
Aporturile in procente ale factorilor constanti si variabili la venitul din toate produsele,sunt :
e) Aportul factorilor constanti : APTO(I) = MPTO(I) / MPTT(I)
f) Aportul factorilor variabili : APXT(I) = MPXT(I) / MPTT(I)
g) Aportul interactiunilor factorilor variabili :
APIXT(I) = MPIXT(I) / MPTT(I) = 1 - APTO(I) - APXT(I)
Calculul aporturilor de la punctele A-D se poate face atat pentru dozele curente XO(I,J) cat si pentru dozele celor sase optime din sectiunea 2.1 si anume XD(I,J) , XM(I,J) , XE(I,J) , XT(I,J) .
Toate calculele din acest capitol le face programul FPCUB .
3.1 Doi factori si un produs
A.Date de intrare:
M=1 produs(Porumb)
N=2 factori (NPK si apa de irigatie)
Y= {[4X1+0.002X12 - 0.00003X13]+[0.8X2+0.00008X22 - 0.0000001X23]+2.[0.0001X1X2]
Aici X1 este cantitatea de NPK (Kg / ha de porumb) ,X2 este cantitatea de apa de irigatie (m3 apa / ha de porumb) iar Y este productia de porumb(Kg / ha) .
In prima acolada se gaseste productia-martor de porumb (Kg / ha) , nefertilizat chimic si neirigat.
In a doua acolada se gasesc:
in prima paranteza patrata se gaseste productia suplimentara de porumb(Kg / ha) datorata fertilizarii chimice ;
in a doua paranteza patrata se gaseste productia suplimentara de porumb(Kg / ha) datorata irigarii ;
in a treia paranteza patrata se gaseste productia suplimentara de porumb(Kg / ha) datorata interactiunii NPK x apa de irigatie ;
Cheltuieli constante : CC=800 lei / ha
Aceste cheltuieli include toate cheltuielile productive si neproductive
cu trei exceptii:
cheltuielile cu fertilizarea chimica;
cheltuielile cu irigarea;
cheltuielile cu recoltarea si transportul productiei suplimentare de porumb datorata fertilizarii chimice si irigarii .
Costurile factorilor : CF1=0.8 lei / Kg NPK ; CF2 =0.09 lei / m3 apa .
Cheltuieli cu recoltarea si transportul porumbului : CR =0.04 lei / Kg porumb
Pretul de vanzare al porumbului : PV=0.7 lei / Kg porumb
Suprafata cultivata : S=20 ha
B.REZULTATE :
a) Productii-martor
Productia fizica-martor Y0 = 60000kg porumb ;
Venitul-martor V0 = 42000 lei ;
Cheltuielile-martor C0 = 18400 lei ;
Profitul-martor P0 = 23600 lei ;
Productia unitara-martor YU0 = 3000 Kg porumb boabe / Ha .
Cheltuielile unitare-martor CY0 = 0.31 lei cheltuieli / 1 Kg porumb boabe
Rata profitului martor RP0 = 1.283 lei profit / 1 leu cheltuit
b) Optime in alocarea de resurse :
I. OPTIMUL MARGINAL
Se realizeaza pentru x1= 22 Kg NPK / Ha si x2 = 266 m3 apa / Ha.
Rezulta productia suplimentara YS = 6157 Kg porumb boabe ; venitul suplimentar
VS = 4310 lei ; cheltuielile suplimentare CS = 1081.8 lei si profitul suplimentar PS =
3228.2 lei . Aceste valori se adaoga celor de la martor de la punctul a).
Productia fizica unitara totala este YUT = 3307 Kg porumb boabe / Ha .
Cheltuielile unitare totale sunt CYT = 0.2945 lei cheltuieli / 1 Kg porumb boabe.
Rata profitului total este RPT = 1.377 lei profit / 1 leu cheltuit .
Deoarece YUT > YU0 , CYT < CY0 si RPT > RP0 , merita sa folosim dozele optimului marginal.
Tabel cu indicatorii economici ai optimului marginal
|
Indicatori economici |
Profit suplimentar |
Rata profit Suplimentar |
Rata substituire Factori |
|
Medii |
1.8947 lei |
1.967 lei | |
|
0.4503 lei |
3.669 lei |
||
|
Marginali |
1.9045 lei = Maxim |
1.976 lei = Maxim | |
|
0.4550 lei = Maxim |
3.698 lei = Maxim |
||
|
Elasticitati | |||
COMENTARIU ASUPRA TABELULUI :
1) Coloana profitului suplimentar :
Fiecare din cele 22 Kg NPK / Ha a adus un profit suplimentar de 1.8947 lei.
Fiecare din cei 266 m3 apa / Ha a adus un profit suplimentar 0.4503 lei .
Al 23-lea Kg NPK / Ha ar creste profitul suplimentar cu valoarea maxima de
1.9045 lei .
Al 267-lea m3 apa / Ha ar creste profitul suplimentar cu valoarea maxima de
0.4550 lei .
Cresterea dozei de 22 Kg NPK / Ha cu inca 1 % ar creste profitul suplimentar
cu inca 1.005 % .
Cresterea dozei de 266 m3 apa / Ha cu inca 1 % ar creste profitul suplimentar
cu inca 1.010 % .
2) Coloana ratei profitului suplimentar :
Fiecare leu cheltuit cu fertilizarea chimica din suma de 1081.8 lei a adus un profit
suplimentar de 1.967 lei.
Fiecare leu cheltuit cu irigarea din suma de 1081.8 lei a adus un profit suplimentar de 3.669 lei.
Inca un leu cheltuit cu fertilizarea chimica peste suma de 1081.8 lei ar creste profitul
suplimentar cu valoarea maxima de 1.976 lei.
Inca un leu cheltuit cu irigarea peste suma de 1081.8 lei ar creste profitul suplimentar
cu valoarea maxima de 3.698 lei.
Cresterea cheltuielilor cu fertilizarea chimica cu inca 1 % peste suma de 1081.8 lei ar
creste profitul suplimentar cu inca 1.005 % .
Cresterea cheltuielilor cu irigarea cu inca 1 % peste suma de 1081.8 lei ar creste profitul suplimentar cu inca 1.008 % .
3) Coloana ratei substituirii factorilor
4.21 m3 apa / Ha din cei 266 m3 apa / Ha au adus acelasi profit ca 1 Kg NPK / Ha din cei 22 Kg NPK / Ha .
4.19 m3 / Ha crestere apa fata de cei 266 m3 apa / Ha si 1 Kg / Ha crestere NPK fata de cei 22 Kg NPK / Ha ar creste profitul cu aceeasi suma.
0.99 % crestere apa fata de cei 266 m3 apa / Ha si 1 % crestere NPK fata de cei 22 Kg NPK / Ha, ar creste profitul cu acelasi numar de procente.
II. OPTIMUL DE ECHILIBRU
Se realizeaza pentru x1= 33 Kg NPK / HA si x2 = 400 m3 apa / Ha.
Rezulta productia suplimentara YS = 9270 Kg porumb boabe ; venitul suplimentar
VS = 6489.2 lei ; cheltuielile suplimentare CS = 1624.1 lei si profitul suplimentar PS =
4865.1 lei . Aceste valori se adaoga celor de la martor de la punctul a).
Productia unitara totala este YUT = 3463 Kg porumb boabe / Ha .
Cheltuielile unitare totale sunt CYT = 0.2890 lei cheltuieli / 1 Kg porumb boabe.
Rata profitului total este RPT = 1.421 lei profit / 1 leu cheltuit .
Deoarece YUT > YU0 , CYT < CY0 si RPT > RP0 , merita sa folosim dozele optimului de echilibru.
Tabel cu indicatorii economici ai optimului de echilibru
|
Indicatori economici |
Profit suplimentar |
Rata profit Suplimentar |
Rata substituire Factori |
|
Medii |
1.9148 lei |
1.985 lei =Maxim | |
|
0.4529 lei |
3.685 lei = Maxim |
||
|
Marginali |
1.9148 lei |
1.985 lei = Maxim | |
|
0.4529 lei |
3.685 lei = Maxim |
||
|
Elasticitati |
1 % |
||
COMENTARIU ASUPRA TABELULUI :
1) Coloana profitului suplimentar :
Fiecare din cele 33 Kg NPK / Ha a adus un profit suplimentar maxim de 1.9148 lei.
Fiecare din cei 400 m3 apa / Ha a adus un profit suplimentar maxim de 0.4529 lei .
Al 34-lea Kg NPK / Ha ar creste profitul suplimentar tot cu cu 1.9148 lei .
Al 401-lea m3 apa / Ha ar creste profitul suplimentar tot cu 0.4529 lei .
Cresterea dozei de 33 Kg NPK / Ha cu inca 1 % ar creste profitul suplimentar
tot cu 1 % ( cresterea procentuala de efort fizic pentru factorul NPK este egala cu cresterea procentuala de efect pentru profit).
Cresterea dozei de 400 m3 apa / Ha cu inca 1 % ar creste profitul suplimentar tot cu 1 % ( cresterea procentuala de efort fizic pentru factorul Apa este egala cu cresterea procentuala de efect pentru profit).
2) Coloana ratei profitului suplimentar :
Fiecare leu cheltuit cu fertilizarea chimica din suma de 1624.1 lei a adus un profit
suplimentar maxim de 1.985 lei.
Fiecare leu cheltuit cu irigarea din suma de 1624.1 lei a adus un profit suplimentar maxim de 3.685 lei.
Inca un leu cheltuit cu fertilizarea chimica peste suma de 1624.1 lei ar creste profitul
suplimentar tot cu 1.985 lei.
Inca un leu cheltuit cu irigarea peste suma de 1624.1 lei ar creste profitul suplimentar
tot cu 3.685 lei.
Cresterea cheltuielilor cu fertilizarea chimica cu inca 1 % peste suma de 1624.1 lei ar
creste profitul suplimentar tot cu 1 % ( cresterea procentuala de efort financiar pentru factorul NPK este egala cu cresterea procentuala de efect pentru profit).
Cresterea cheltuielilor cu irigarea cu inca 1 % peste suma de 1624.1 lei ar creste profitul suplimentar tot cu 1 % ( cresterea procentuala de efort financiar pentru factorul NPK este egala cu cresterea procentuala de efect pentru profit).
3) Coloana ratei substituirii factorilor
4.23 m3 apa / Ha din cei 400 m3 apa / Ha au adus acelasi profit ca 1 Kg NPK / Ha din cei 33 Kg NPK / Ha .
4.23 m3 / Ha crestere apa fata de cei 400 m3 apa / Ha si 1 Kg / Ha crestere NPK fata de cei 33 Kg NPK / Ha ar creste profitul cu aceeasi suma.
1 % crestere apa fata de cei 400 m3 apa / Ha si 1 % crestere NPK fata de cei 33 Kg NPK / Ha, ar creste profitul cu acelasi numar de procente ( cresterea procentuala de efort fizic pentru factorul NPK este egala cu cresterea procentuala de efort fizic pentru Apa sub aspectul aceleiasi cresteri valorice a profitului).
Se realizeaza pentru x1= 210 Kg NPK / Ha si x2 = 1823 m3 apa / Ha.
Rezulta productia suplimentara YS = 36925 Kg porumb boabe ; venitul suplimentar
VS = 25847.9 lei ; cheltuielile suplimentare CS = 8130.4 lei si profitul suplimentar maxim PS = 17717.5 lei . Aceste valori se adaoga celor de la martor de la punctul a).
Productia unitara totala este YUT = 4846 Kg porumb boabe / Ha .
Cheltuielile unitare totale minime sunt CYT = 0.2737 lei cheltuieli / 1 Kg porumb boabe.
Rata profitului total maxima este RPT = 1.558 lei profit / 1 leu cheltuit .
Deoarece YUT > YU0 , CYT < CY0 si RPT > RP0 , merita sa folosim dozele optimului economic.
Tabel cu indicatorii economici ai optimului economic
|
Indicatori economici |
Profit suplimentar |
Rata profit Suplimentar |
Rata substituire Factori |
|
Medii |
1.4798 lei |
1.577 lei | |
|
0.3426 lei |
2.948 lei |
||
|
Marginali |
0 lei |
0 lei | |
|
0 lei |
0 lei |
||
|
Elasticitati | |||
COMENTARIU ASUPRA TABELULUI :
1) Coloana profitului suplimentar :
Fiecare din cele 210 Kg NPK / Ha a adus un profit suplimentar de 1.4798 lei.
Fiecare din cei 1823 m3 apa / Ha a adus un profit suplimentar 0.3426 lei .
Al 211-lea Kg NPK / Ha ar creste venitul suplimentar cu aceeasi suma cu care ar
creste si cheltuielile deci profitul din fertilizare ar creste cu 0 lei , fiind deja maxim.
Al 1824-lea m3 apa / Ha ar creste venitul suplimentar cu aceeasi suma cu care ar
creste si cheltuielile deci profitul din irigare ar creste cu 0 lei , fiind deja maxim.
Cresterea dozei de 210 Kg NPK / Ha cu inca 1 % ar creste venitul suplimentar
cu acelasi numar de procente cu care ar creste si cheltuielile deci profitul suplimentar
din fertilizare ar creste cu 0 % , fiind deja maxim.
Cresterea dozei de 1823 m3 apa / Ha cu inca 1 % ar creste venitul suplimentar
cu acelasi numar de procente cu care ar creste si cheltuielile deci profitul suplimentar
din irigare ar creste cu 0 % fiind deja maxim.
2) Coloana ratei profitului suplimentar :
Fiecare leu cheltuit cu fertilizarea chimica din suma de 8130.4 lei a adus un profit
suplimentar de 1.577 lei.
Fiecare leu cheltuit cu irigarea din suma de 8130.4 lei a adus un profit suplimentar de 2.948 lei.
Inca un leu cheltuit cu fertilizarea chimica peste suma de 8130.4 lei ar creste venitul
suplimentar tot cu un leu deci profitul suplimentar din fertilizare ar creste cu 0 lei , fiind deja maxim .
Inca un leu cheltuit cu irigarea peste suma de 8130.4 lei ar creste venitul suplimentar tot cu un leu deci profitul suplimentar din irirgare ar creste cu 0 lei , fiind deja maxim .
Cresterea cheltuielilor cu fertilizarea chimica cu inca 1 % peste suma de 8130.4 lei ar
creste venitul suplimentar cu acelasi numar de procente cu care ar creste si cheltuielile deci profitul din fertilizare ar creste cu 0 % , fiind deja maxim .
Cresterea cheltuielilor cu fertilizarea chimica cu inca 1 % peste suma de 8130.4 lei ar
creste venitul suplimentar cu acelasi numar de procente cu care ar creste si cheltuielile deci profitul din fertilizare ar creste cu 0 % , fiind deja maxim .
3) Coloana ratei substituirii factorilor
4.32 m3 apa / Ha din cei 1823 m3 / Ha au adus acelasi profit ca 1 Kg NPK / Ha din cei 210 Kg NPK / Ha .
Orice crestere valorica a apei fata de cei 1823 m3 / Ha si orice crestere valorica a NPK fata de cei 210 Kg NPK / Ha ar creste profitul cu 0 lei , fiind deja maxim.
Orice crestere procentuala a apei fata de cei 1823 m3 / Ha si orice crestere procentuala a NPK fata de cei 210 Kg NPK / Ha ar creste profitul cu 0 % , fiind deja maxim.
IV. OPTIMUL TEHNIC
Se realizeaza pentru x1= 244 Kg NPK / Ha si x2 = 1969 m3 apa / Ha.
Rezulta productia suplimentara maxima YS = 37546 Kg porumb boabe ; venitul suplimentar maxim VS = 26282.8 lei ; cheltuielile suplimentare CS = 8956.2 lei si profitul suplimentar PS = 17326.6 lei . Aceste valori se adaoga celor de la martor de la punctul a).
Productia unitara totala maxima este YUT = 4877 Kg porumb boabe / Ha .
Cheltuielile unitare totale sunt CYT = 0.2804 lei cheltuieli / 1 Kg porumb boabe.
Rata profitului total este RPT = 1.496 lei profit / 1 leu cheltuit .
Deoarece YUT > YU0 , CYT < CY0 si RPT > RP0 , merita sa folosim dozele optimului tehnic.
Tabel cu indicatorii economici ai optimului tehnic
|
Indicatori economici |
Profit suplimentar |
Rata profit Suplimentar |
Rata substituire Factori |
|
Medii |
1.2408 lei |
1.343 lei | |
|
0.3181 lei |
2.773 lei |
||
|
Marginali |
- 0.8 lei |
- 1 leu | |
|
- 0.09 lei |
- 1 leu |
||
|
Elasticitati | |||
COMENTARIU ASUPRA TABELULUI :
1) Coloana profitului suplimentar :
Fiecare din cele 244 Kg NPK / Ha a adus un profit suplimentar de 1.2408 lei.
Fiecare din cei 1969 m3 apa / Ha a adus un profit suplimentar 0.3181 lei .
Al 245-lea Kg NPK / Ha ar creste venitul suplimentar cu 0 lei , fiind deja maxim iar cheltuielile ar creste cu 0.8 lei(costul celui de al 245-lea Kg NPK / Ha )deci profitul din fertilizare ar scade cu 0.8 lei .
Al 1970-lea m3 apa / Ha ar creste venitul suplimentar cu 0 lei , fiind deja maxim iar cheltuielile suplimentare ar creste cu 0.09 lei (costul celui de al 1970-lea m3 apa / Ha ) deci profitul din irigare ar scade cu 0.09 lei .
Cresterea dozei de 244 Kg NPK / Ha cu inca 1 % ar creste venitul suplimentar cu 0 % , fiind deja maxim iar cheltuielile suplimentare ar creste cu 0.64 % deci profitul suplimentar din fertilizare ar scade cu 0.64 % .
Cresterea dozei de 1969 m3 apa / Ha cu inca 1 % ar creste venitul suplimentar cu 0 % iar cheltuielile suplimentare ar creste cu 0.28 % deci profitul suplimentar din irigare ar scade cu 0.28 % .
2) Coloana ratei profitului suplimentar :
Fiecare leu cheltuit cu fertilizarea chimica din suma de 8956.2 lei a adus un profit suplimentar de 1.343 lei.
Fiecare leu cheltuit cu irigarea din suma de 8956.2 lei a adus un profit suplimentar de 2.773 lei.
Inca un leu cheltuit cu fertilizarea chimica peste suma de 8956.2 lei ar creste venitul
suplimentar cu 0 lei , fiind deja maxim iar cheltuielile ar creste cu un leu deci profitul suplimentar din fertilizare ar scade cu un leu .
Inca un leu cheltuit cu irigarea peste suma de 8956.2 lei ar creste venitul suplimentar tot cu 0 lei , fiind deja maxim iar cheltuielile suplimentare ar creste cu un leu deci profitul suplimentar din irigare ar scade cu un leu .
Cresterea cheltuielilor cu fertilizarea chimica cu inca 1 % peste suma de 8956.2 lei ar
creste venitul suplimentar cu 0 % si cheltuielile ar creste cu 1 % deci profitul din fertilizare ar scade cu 1 % .
Cresterea cheltuielilor cu irigarea cu inca 1 % peste suma de 8956.2 lei ar creste venitul suplimentar cu 0 % si cheltuielile suplimentare ar creste cu 1 % deci profitul din fertilizare ar scade cu 1 % .
3) Coloana ratei substituirii factorilor
3.9 m3 apa / Ha din cei 1969 m3 apa / Ha au adus acelasi profit ca 1 Kg NPK / Ha din cei 244 Kg NPK / Ha .
8.9 m3 / Ha crestere apa fata de cei 1969 m3 apa / Ha si 1 Kg / Ha crestere NPK fata de cei 244 Kg NPK / Ha ar scade profitul cu aceeasi suma.
2.28 % crestere apa fata de cei 1969 m3 apa / Ha si 1 % crestere NPK fata de cei 244
Kg NPK / Ha , ar scade profitul cu acelasi numar de procente.
V. MAXIM DE VENIT CU CHELTUIELI LIMITATE (7595.8 lei)
Se realizeaza pentru x1= 189 Kg NPK / Ha si x2 = 1736 m3 apa / Ha.
Rezulta productia suplimentara maxima conditionata YS = 35964 Kg porumb boabe ; venitul suplimentar maxim conditionat VS = 25175.2 lei ; cheltuielile suplimentare date CS = 7595.8 lei si profitul suplimentar maxim conditionat PS = 17579.8 lei . Aceste valori se adaoga celor de la martor de la punctul a).
Productia fizica unitara totala este YUT = 4798 Kg porumb boabe / Ha .
Cheltuielile unitare totale sunt CYT = 0.2708 lei cheltuieli / 1 Kg porumb boabe.
Rata profitului total este RPT = 1.584 lei profit / 1 leu cheltuit .
Deoarece YUT > YU0 , CYT < CY0 si RPT > RP0 , merita sa folosim dozele maximului de venit cu cheltuieli limitate .
Tabel cu indicatorii economici ai maximului de venit cu cheltuieli limitate
|
Indicatori economici |
Profit suplimentar |
Rata profit Suplimentar |
Rata substituire Factori |
|
Medii |
1.6086 lei |
1.700 lei | |
|
0.3556 lei |
3.039 lei |
||
|
Marginali |
0.4375 lei |
0.500 lei | |
|
0.0492 lei |
0.500 lei = Maxim |
||
|
Elasticitati | |||
COMENTARIU ASUPRA TABELULUI :
1) Coloana profitului suplimentar :
Fiecare din cele 189 Kg NPK / Ha a adus un profit suplimentar de 1.6086 lei.
Fiecare din cei 1736 m3 apa / Ha a adus un profit suplimentar 0.3556 lei .
Al 190-lea Kg NPK / Ha ar creste profitul suplimentar cu valoarea de 0.4375 lei .
Al 1737-lea m3 apa / Ha ar creste profitul suplimentar cu valoarea de 0.0492 lei .
Cresterea dozei de 189 Kg NPK / Ha cu inca 1 % ar creste profitul suplimentar
cu inca 0.27 % .
Cresterea dozei de 1736 m3 apa / Ha cu inca 1 % ar creste profitul suplimentar
cu inca 0.14 % .
2) Coloana ratei profitului suplimentar :
Fiecare leu cheltuit cu fertilizarea chimica din suma data de 7595.8 lei a adus un profit suplimentar de 1.700 lei.
Fiecare leu cheltuit cu irigarea din suma data de 7595.8 lei a adus un profit suplimentar de 3.039 lei.
Inca un leu cheltuit cu fertilizarea chimica peste suma data de 7595.8 lei ar creste profitul suplimentar cu valoarea de 0.5 lei.
Inca un leu cheltuit cu irigarea peste suma de 7595.8 lei ar creste profitul suplimentar
cu valoarea maxima de 0.5 lei.
Cresterea cheltuielilor cu fertilizarea chimica cu inca 1 % peste suma de 7595.8 lei ar
creste profitul suplimentar cu inca 0.29 % .
Cresterea cheltuielilor cu irigarea cu inca 1 % peste suma de 7595.8 lei ar creste profitul suplimentar cu inca 0.16 % .
3) Coloana ratei substituirii factorilor
4.5 m3 apa / Ha din cei 1736 m3 apa / Ha au adus acelasi profit ca 1 Kg NPK / Ha din cei 189 Kg NPK / Ha .
8.9 m3 / Ha crestere apa fata de cei 1736 m3 apa / Ha si 1 Kg / Ha crestere NPK fata de cei 189 Kg NPK / Ha ar creste profitul cu aceeasi suma.
1.98 % crestere apa fata de cei 1736 m3 apa / Ha si 1 % crestere NPK fata de cei 189 Kg NPK / Ha, ar creste profitul cu acelasi numar de procente.
VI. MINIM DE CHELTUIELI CU VENIT GARANTAT (24548.7 lei)
Se realizeaza pentru x1= 174 Kg NPK / Ha si x2 = 1678 m3 apa / Ha.
Rezulta productia suplimentara data YS = 35069 Kg porumb boabe ; venitul suplimentar dat VS = 24548.7 lei ; cheltuielile suplimentare minime conditionate CS = 7216.8 lei si profitul suplimentar maxim conditionat PS = 17331.8 lei . Aceste valori se adaoga celor de la martor de la punctul a).
Productia fizica unitara totala este YUT = 4753 Kg porumb boabe / Ha .
Cheltuielile unitare totale sunt CYT = 0.2695 lei cheltuieli / 1 Kg porumb boabe.
Rata profitului total este RPT = 1.598 lei profit / 1 leu cheltuit .
Deoarece YUT > YU0 , CYT < CY0 si RPT > RP0 , merita sa folosim dozele minimului de cheltuieli cu venit garantat .
Tabel cu indicatorii economici ai maximului de venit cu cheltuieli limitate
|
Indicatori economici |
Profit suplimentar |
Rata profit Suplimentar |
Rata substituire Factori |
|
Medii |
1.6989 lei |
1.776 lei | |
|
0.3636 lei |
3.095 lei |
||
|
Marginali |
0.7133 lei |
0.800 lei | |
|
0.0802 lei |
0.800 lei |
||
|
Elasticitati | |||
COMENTARIU ASUPRA TABELULUI :
1) Coloana profitului suplimentar :
Fiecare din cele 174 Kg NPK / Ha a adus un profit suplimentar de 1.6889 lei.
Fiecare din cei 1678 m3 apa / Ha a adus un profit suplimentar 0.3636 lei .
Al 175-lea Kg NPK / Ha ar creste profitul suplimentar cu valoarea de 0.7133 lei .
Al 1679-lea m3 apa / Ha ar creste profitul suplimentar cu valoarea de 0.0802 lei .
Cresterea dozei de 174 Kg NPK / Ha cu inca 1 % ar creste profitul suplimentar
cu inca 0.42 % .
Cresterea dozei de 1678 m3 apa / Ha cu inca 1 % ar creste profitul suplimentar
cu inca 0.22 % .
2) Coloana ratei profitului suplimentar :
Fiecare leu cheltuit cu fertilizarea chimica din suma minima de 7216.8 lei a adus un profit suplimentar de 1.776 lei.
Fiecare leu cheltuit cu irigarea din suma minima de 7216.8 lei a adus un profit suplimentar de 3.095 lei.
Inca un leu cheltuit cu fertilizarea chimica peste suma minima de 7216.8 lei ar creste profitul suplimentar cu valoarea de 0.8 lei.
Inca un leu cheltuit cu irigarea peste suma minima de 7216.8 lei ar creste profitul suplimentar cu valoarea de 0.8 lei.
Cresterea cheltuielilor cu fertilizarea chimica cu inca 1 % peste suma de 7216.8 lei ar
creste profitul suplimentar cu inca 0.45 % .
Cresterea cheltuielilor cu irigarea cu inca 1 % peste suma de 7216.8 lei ar creste profitul suplimentar cu inca 0.26 % .
3) Coloana ratei substituirii factorilor
4.6 m3 apa / Ha din cei 1678 m3 apa / Ha au adus acelasi profit ca 1 Kg NPK / Ha din cei 174 Kg NPK / Ha .
8.9 m3 / Ha crestere apa fata de cei 1678 m3 apa / Ha si 1 Kg / Ha crestere NPK fata de cei 174 Kg NPK / Ha ar creste profitul cu aceeasi suma.
1.93 % crestere apa fata de cei 1678 m3 apa / Ha si 1 % crestere NPK fata de cei 174 Kg NPK / Ha, ar creste profitul cu acelasi numar de procente.
VII . Dozele de rentabilitate (cu profit nul)
Sunt x1 = 304 Kg NPK / Ha ; x2 = 2576 m3 apa / Ha .
3.2 Un factor si doua produse
A.Date de intrare:
1) M=2 produse : (Grau si Porumb)
2) N=1 factor (NPK).
3) Y1 = [2000]+[3X1+0.015X12 - 0.00002X1
Y2 = [3000]+[4X2+0.002X22 - 0.0003X2
Aici X1 este cantitatea de NPK (Kg / ha de grau) ,X2 este cantitatea de NPK (Kg / ha de porumb) iar Y1 este productia de grau (Kg / ha) ,Y2 este productia de porumb(Kg / ha) .
In prima paranteza patrata din membrul doi al lui Y 1 se gaseste productia-martor de grau (Kg / ha) , nefertilizat chimic .
In a doua paranteza patrata din membrul doi al lui Y1 se gaseste productia suplimentara de grau datotrata fertilizarii .
Semnificatia celor doua paranteze patrate din membrul doi al lui Y2 este analoaga pentru porumb.
Cheltuieli constante : CC=( 780 lei / ha grau ; 800 lei / ha porumb)
Aceste cheltuieli include toate cheltuielile productive si neproductive
cu doua exceptii:
cheltuielile cu fertilizarea chimica;
cheltuielile cu recoltarea si transportul productiei suplimentare de grau respectiv porumb datorata fertilizarii chimice.
5) Costul factorului : CF=0.8 lei / Kg NPK
6) Cheltuieli cu recoltarea si transportul : CR1 = 0.045 lei / Kg grau ; CR2 = 0.04 lei / Kg porumb .
7) Preturile de vanzare ale produselor : PV1= 0.6 lei / Kg grau ;
PV2 = 0.7 lei /Kg porumb.
8) Suprafete cultivate : S1 =10 ha grau ; S2 = 20 ha porumb
B.Rezultate
a)Productii-martor
Productia fizica-martor de grau Y10 = 20000kg ;
Productia fizica-martor de porumb Y20 = 60000kg
Venitul-martor V0 = 54000 lei ;
Cheltuielile-martor C0 = 27100 lei ;
Profitul-martor P0 = 26900 lei ;
Productiile unitare-martor :YU10 = 2000 Kg grau / Ha ; YU20 = 3000 Kg porumb / Ha
Cheltuielile unitare-martor : CY10 = 0.4350 lei / Kg grau ; CY20 =0.3067 lei / Kg porumb
Rata profitului martor RP0 = 0.992 lei profit / 1 leu cheltuit
d) Optime in alocarea de resurse
I. OPTIMUL MARGINAL
Se realizeaza pentru x1= 25 Kg NPK / Ha grau si x2 = 22 Kg NPK / Ha porumb.
Rezulta productiile suplimentare YS1 = 756 Kg grau , YS2 = 1790 Kg porumb ; venitul suplimentar VS = 1707.4 lei ; cheltuielile suplimentare CS = 661.2 lei din care CS1 = 234 lei pentru fertilizarea graului si CS2 = 427.2 lei pentru fertilizarea porumbului ; profitul suplimentar PS = 1046.2 lei . Aceste valori se adaoga celor de la martor de la punctul a).
Productiile unitare totale sunt YUT1 = 2076 Kg grau / Ha ; YUT2 = 3090 Kg porumb / Ha .
Cheltuielile unitare totale sunt CYT1 = 0.4304 lei cheltuieli / 1 Kg grau si CYT2 = 0.3047 lei cheltuieli / 1 Kg Porumb .
Rata profitului total este RPT = 1.006 lei profit / 1 leu cheltuit .
Deoarece YUTi > YUi 0 , CYTi < CYi 0 si RPT > RP0 , merita sa folosim dozele optimului marginal.
Tabel cu indicatorii economici ai optimului marginal
|
Indicatori Economici |
Profit suplimentar |
Rata profitului suplimentar |
Rata Valorificare Factor |
||
|
Medii |
0.8788 lei |
1.8595 lei |
0.939 lei |
1.934 lei | |
|
Marginali |
0.8858 lei = Maxim |
1.8693 lei = Maxim |
0.945 lei = Maxim |
1.943 lei = Maxim | |
|
Elasticitati | |||||
COMENTARIU ASUPRA TABELULUI :
1) Coloana profitului suplimentar :
Fiecare din cele 25 Kg NPK / Ha grau a adus un profit suplimentar de 0.8788 lei.
Fiecare din cei 22 Kg NPK / Ha porumb a adus un profit suplimentar 1.8595 lei .
Al 26-lea Kg NPK / Ha grau ar creste profitul suplimentar cu valoarea maxima de
0.8858 lei .
Al 23-lea Kg NPK / Ha porumb ar creste profitul suplimentar cu valoarea maxima de
1.8693 lei .
Cresterea dozei de 25 Kg NPK / Ha grau cu inca 1 % ar creste profitul suplimentar
cu inca 1.008 % .
Cresterea dozei de 22 Kg NPK / Ha porumb cu inca 1 % ar creste profitul suplimentar cu inca 1.006 % .
2) Coloana ratei profitului suplimentar :
Fiecare leu cheltuit cu fertilizarea chimica a graului din suma de 234 lei a adus un profit suplimentar de 0.939 lei.
Fiecare leu cheltuit cu fertilizarea chimica a porumbului din suma de 427.2 lei a adus un profit suplimentar de 1.934 lei.
Inca un leu cheltuit cu fertilizarea chimica a graului peste suma de 234 lei ar creste profitul suplimentar cu valoarea maxima de .945 lei.
Inca un leu cheltuit cu fertilizarea chimica a porumbului peste suma de 427.2 lei ar creste profitul suplimentar cu valoarea maxima de 1.943 lei.
Cresterea cheltuielilor cu fertilizarea chimica a graului cu inca 1 % peste suma de 234 lei ar creste profitul suplimentar cu inca 1.008 % .
Cresterea cheltuielilor cu fertilizarea chimica a porumbului cu inca 1 % peste suma de 427.2 lei ar creste profitul suplimentar cu inca 1.004 % .
3) Coloana ratei substituirii factorilor
0.472 Kg NPK / Ha porumb din cei 22 Kg NPK / Ha porumb au adus acelasi profit ca 1 Kg NPK / Ha grau din cei 25 Kg NPK / Ha porumb.
0.474 Kg / Ha porumb crestere NPK fata de cele 22 Kg NPK / Ha porumb si 1 Kg / Ha grau crestere NPK fata de cele 25 Kg NPK / Ha grau ar creste profitul cu aceeasi suma.
1.002 % crestere NPK fata de cele 22 Kg NPK / Ha porumb si 1 % crestere NPK fata de cele 25 Kg NPK / Ha grau , ar creste profitul cu acelasi numar de procente.
II. OPTIMUL DE ECHILIBRU
Se realizeaza pentru x1= 37 Kg NPK / Ha grau si x2 = 33 Kg NPK / Ha porumb.
Rezulta productiile suplimentare YS1 = 1135 Kg grau ; YS2 = 2688 Kg porumb ; venitul suplimentar VS = 2563.6 lei ; cheltuielile suplimentare CS = 992 lei din care
CS1 = 351.1 lei pentru fertilizarea graului si CS2 = 640.9 lei pentru fertilizarea porumbului ; profitul suplimentar PS = 1571.6 lei . Aceste valori se adaoga celor de la martor de la punctul a).
Productiile unitare totale sunt YUT1 = 2114 Kg grau / Ha ; YUT2 = 3134 Kg porumb / Ha .
Cheltuielile unitare totale sunt CYT1 = 0.4282 lei cheltuieli / 1 Kg grau si CYT2 =
0.3134 lei cheltuieli / Kg porumb .
Rata profitului total este RPT = 1.013 lei profit / 1 leu cheltuit .
Deoarece YUT > YU0 , CYT < CY0 si RPT > RP0 , merita sa folosim dozele optimului de echilibru.
Tabel cu indicatorii economici ai optimului de echilibru
|
Indicatori Economici |
Profit suplimentar |
Rata profitului suplimentar |
Rata Valorificare Factor |
||
|
Medii |
0.8806 lei = Maxim |
1.8620 lei = Maxim |
0.940 lei = Maxim |
1.937 lei = Maxim | |
|
Marginali |
0.8806 lei |
1.8620 lei |
0.940 lei |
1.937 lei | |
|
Elasticitati | |||||
COMENTARIU ASUPRA TABELULUI :
1) Coloana profitului suplimentar :
Fiecare din cele 37 Kg NPK / Ha grau a adus un profit suplimentar maxim de 0.8806 lei.
Fiecare din cei 33 Kg NPK / Ha porumb a adus un profit suplimentar maxim de 1.8620 lei .
Al 38-lea Kg NPK / Ha grau ar creste profitul suplimentar tot cu cu 0.8806 lei .
Al 34-lea Kg NPK / Ha porumb ar creste profitul suplimentar tot cu 1.8620 lei .
Cresterea dozei de 33 Kg NPK / Ha grau cu inca 1 % ar creste profitul suplimentar
tot cu 1 % ( cresterea procentuala de efort fizic pentru factorul NPK la grau este egala cu cresterea procentuala de efect pentru profit din grau).
Cresterea dozei de 33 Kg NPK / Ha porumb cu inca 1 % ar creste profitul suplimentar tot cu 1 % ( cresterea procentuala de efort fizic pentru factorul NPK la porumb este egala cu cresterea procentuala de efect pentru profit din porumb).
2) Coloana ratei profitului suplimentar :
Fiecare leu cheltuit cu fertilizarea chimica a griului din suma de 351.1 lei a adus un profit suplimentar maxim de 0.940 lei.
Fiecare leu cheltuit cu fertilizarea chimica a porumbului din suma de 640.9 lei a adus un profit suplimentar maxim de 1.937 lei.
Inca un leu cheltuit cu fertilizarea chimica a graului peste suma de 351.1 lei ar creste profitul suplimentar tot cu 0.940 lei.
Inca un leu cheltuit cu fertilizarea chimica a porumbului peste suma de 640.9 lei ar creste profitul suplimentar tot cu 1.937 lei.
Cresterea cheltuielilor cu fertilizarea chimica a graului cu inca 1 % peste suma de 351.1 lei ar creste profitul suplimentar tot cu 1 % ( cresterea procentuala de efort financiar pentru factorul NPK la grau este egala cu cresterea procentuala de efect pentru profitul din grau ).
Cresterea cheltuielilor cu fertilizarea chimica a porumbului cu inca 1 % peste suma de 640.9 lei ar creste profitul suplimentar tot cu 1 % ( cresterea procentuala de efort financiar pentru factorul NPK la porumb este egala cu cresterea procentuala de efect pentru profitul din porumb).
3) Coloana ratei substituirii factorilor
0.473 Kg NPK / Ha porumb din cele 33 Kg NPK / Ha porumb au adus acelasi profit ca 1 Kg NPK / Ha grau din cele 37 Kg NPK / Ha grau .
0.473 Kg / Ha porumb crestere NPK fata de cele 33 Kg NPK / Ha porumb si 1 Kg / Ha grau crestere NPK fata de cele 37 Kg NPK / Ha grau ar creste profitul cu aceeasi suma.
1 % crestere NPK fata de cele 33 Kg NPK / Ha porumb si 1 % crestere NPK fata de cei 37 Kg NPK / Ha grau , ar creste profitul cu acelasi numar de procente ( cresterea procentuala de efort fizic pentru factorul NPK la grau este egala cu cresterea procentuala de efort fizic pentru NPK la porumb sub aspectul aceleiasi cresteri procentuale a profitului).
Se realizeaza pentru x1= 190 Kg NPK / Ha grau si x2 = 199 Kg NPK / Ha porumb.
Rezulta productiiile suplimentare YS1 = 4871 Kg grau ; YS2 = 12790 Kg porumb ; venitul suplimentar VS = 11876.5 lei ; cheltuielile suplimentare CS = 5445.8 lei din care CS1 = 1740.3 lei pentru fertilizarea graului si CS2 = 3705.6 lei pentru fertilizarea porumbului ; profitul suplimentar maxim PS = 6430.7 lei . Aceste valori se adaoga celor de la martor de la punctul a).
Productiile unitare totale sunt YUT1 = 2487 Kg grau / Ha si YUT2 = 3640 Kg porumb / Ha .
Cheltuielile unitare totale minime sunt CYT1 = 0.4198 lei cheltuieli / 1 Kg grau si
CYT2 = 3037 lei / Kg porumb .
Rata profitului total maxima este RPT = 1.024 lei profit / 1 leu cheltuit .
Deoarece YUT > YU0 , CYT < CY0 si RPT > RP0 , merita sa folosim dozele optimului economic.
Tabel cu indicatorii economici ai optimului economic
|
Indicatori Economici |
Profit suplimentar |
Rata profitului suplimentar |
Rata Valorificare Factor |
||
|
Medii |
0.6220 lei |
1.3144 lei |
0.679 lei |
1.417 lei | |
|
Marginali |
0 lei |
0 lei |
0 lei |
0 lei | |
|
Elasticitati | |||||
COMENTARIU ASUPRA TABELULUI :
1) Coloana profitului suplimentar :
Fiecare din cele 190 Kg NPK / Ha grau a adus un profit suplimentar de 0.6220 lei.
Fiecare din cei 199 Kg NPK / Ha porumb a adus un profit suplimentar 1.3144 lei .
Al 191-lea Kg NPK / Ha grau ar creste venitul suplimentar cu aceeasi suma cu care ar
creste si cheltuielile deci profitul din fertilizare ar creste cu 0 lei , fiind deja maxim.
Al 200-lea Kg NPK / Ha porumb ar creste venitul suplimentar cu aceeasi suma cu care ar creste si cheltuielile deci profitul din irigare ar creste cu 0 lei , fiind deja maxim.
Cresterea dozei de 190 Kg NPK / Ha graucu inca 1 % ar creste venitul suplimentar
cu acelasi numar de procente cu care ar creste si cheltuielile deci profitul suplimentar
din fertilizarea graului ar creste cu 0 % , fiind deja maxim.
Cresterea dozei de 199 Kg NPK / Ha porumb cu inca 1 % ar creste venitul suplimentar cu acelasi numar de procente cu care ar creste si cheltuielile deci profitul suplimentar din fertilizarea porumbului ar creste cu 0 % fiind deja maxim.
2) Coloana ratei profitului suplimentar :
Fiecare leu cheltuit cu fertilizarea chimica a graului din suma de 1740.3 lei a adus un profit suplimentar de 0.679 lei.
Fiecare leu cheltuit cu fertilizarea chimica a porumbului din suma de 3705.6 lei a adus un profit suplimentar de 1.417 lei.
Inca un leu cheltuit cu fertilizarea chimica a graului peste suma de 1740.3 lei ar creste venitul suplimentar tot cu un leu deci profitul suplimentar din fertilizarea graului ar creste cu 0 lei , fiind deja maxim .
Inca un leu cheltuit cu fertilizarea chimica a porumbului peste suma de 3705.6 lei ar creste venitul suplimentar tot cu un leu deci profitul suplimentar din irirgare ar creste cu 0 lei , fiind deja maxim .
Cresterea cheltuielilor cu fertilizarea chimica a graului cu inca 1 % peste suma de 1740.3 lei ar creste venitul suplimentar cu acelasi numar de procente cu care ar creste si cheltuielile deci profitul din fertilizarea griului ar creste cu 0 % , fiind deja maxim .
Cresterea cheltuielilor cu fertilizarea chimica a porumbului cu inca 1 % peste suma de 3705.6 lei ar creste venitul suplimentar cu acelasi numar de procente cu care ar creste si cheltuielile deci profitul din fertilizarea porumbului ar creste cu 0 % , fiind deja maxim .
3) Coloana ratei substituirii factorilor
0.473 Kg NPK / Ha porumb din cei 199 Kg NPK / Ha grau au adus acelasi profit ca 1 Kg NPK / Ha grau din cei 190 Kg NPK / Ha grau .
Orice crestere valorica a NPK fata de cele 199 m3 / Ha porumb si orice crestere valorica a NPK fata de cei 190 Kg NPK / Ha grau ar creste profitul cu 0 lei , fiind deja maxim.
Orice crestere procentuala a NPK fata de cele 199 Kg NPK / Ha porumb si orice crestere procentuala a NPK fata de cele 190 Kg NPK / Ha grau ar creste profitul cu 0 % , fiind deja maxim.
IV. OPTIMUL TEHNIC
Se realizeaza pentru x1= 251 Kg NPK / Ha grau si x2 = 234 Kg NPK / Ha porumb .
Rezulta productiiile suplimentare maxime YS1 = 5312 Kg grau ; YS2 = 13222 Kg porumb ; venitul suplimentar maxim VS = 12443.1 lei ; cheltuielile suplimentare CS = 6524.7 lei din care CS1 = 2248.4 lei pentru fertilizarea graului si CS2 = 4276.2 lei pentru
fertilizarea porumbului ; profitul suplimentar PS = 5918.5 lei . Aceste valori se adaoga celor de la martor de la punctul a).
Productiile unitare totale maxime sunt YUT1 = 2531 Kg grau / Ha si YUT2 = 3661
Kg porumb / Ha .
Cheltuielile unitare totale sunt CYT1 = 0.4325 lei cheltuieli / 1 Kg grau si CYT2 =
3097 lei cheltuieli / 1 Kg porumb .
Rata profitului total este RPT = 0.976 lei profit / 1 leu cheltuit .
Deoarece YUT > YU0 , CYT < CY0 si RPT > RP0 , merita sa folosim dozele optimului tehnic.
Tabel cu indicatorii economici ai optimului tehnic
|
Indicatori Economici |
Profit suplimentar |
Rata profitului suplimentar |
Rata Valorificare Factor |
||
|
Medii |
0.3738 lei |
1.0630 lei |
0.417 lei |
1.165 lei | |
|
Marginali |
- 0.8 lei |
- 0.8 lei |
- 1 leu |
- 1 leu | |
|
Elasticitati | |||||
COMENTARIU ASUPRA TABELULUI :
1) Coloana profitului suplimentar :
Fiecare din cele 251 Kg NPK / Ha grau a adus un profit suplimentar de 0.3738 lei.
Fiecare din cele 234 Kg NPK / Ha porumb a adus un profit suplimentar 1.0630 lei .
Al 252-lea Kg NPK / Ha grau ar creste venitul suplimentar cu 0 lei , fiind deja maxim iar cheltuielile ar creste cu 0.8 lei (costul celui de al 252-lea Kg NPK / Ha )deci profitul din fertilizare ar scade cu 0.8 lei .
Al 235-lea Kg NPK / Ha porumb ar creste venitul suplimentar cu 0 lei , fiind deja maxim iar cheltuielile suplimentare ar creste cu 0.8 lei (costul celui de al 235-lea Kg NPK / Ha porumb) deci profitul din irigare ar scade cu 0.8 lei .
Cresterea dozei de 252 Kg NPK / Ha graucu inca 1 % ar creste venitul suplimentar
cu 0 % , fiind deja maxim iar cheltuielile suplimentare ar creste cu 2.2 % deci profitul suplimentar din fertilizare ar scade cu 2.2 % .
Cresterea dozei de 234 Kg NPK / Ha porumb cu inca 1 % ar creste venitul suplimentar cu 0 % iar cheltuielile suplimentare ar creste cu 0.75 % deci profitul suplimentar din irigare ar scade cu 0.75 % .
2) Coloana ratei profitului suplimentar :
Fiecare leu cheltuit cu fertilizarea chimica a graului din suma de 2248.4 lei a adus un profit suplimentar de 0.417 lei.
Fiecare leu cheltuit cu fertilizarea chimica a porumbului din suma de 4276.2 lei a adus un profit suplimentar de 1.165 lei.
Inca un leu cheltuit cu fertilizarea chimica a graului peste suma de 2248.4 lei ar creste venitul suplimentar cu 0 lei , fiind deja maxim iar cheltuielile ar creste cu un leu deci profitul suplimentar din fertilizarea graului ar scade cu un leu .
Inca un leu cheltuit cu fertilizarea porumbului peste suma de 4276.2 lei ar creste venitul suplimentar tot cu 0 lei , fiind deja maxim iar cheltuielile suplimentare ar creste cu un leu deci profitul suplimentar din fertilizarea porumbului ar scade cu un leu .
Cresterea cheltuielilor cu fertilizarea chimica a graului cu inca 1 % peste suma de 2248.4 lei ar creste venitul suplimentar cu 0 % si cheltuielile ar creste cu 1 % deci profitul din fertilizarea graului ar scade cu 1 % .
Cresterea cheltuielilor cu fertilizarea porumbului cu inca 1 % peste suma de 4276.2 lei ar creste venitul suplimentar cu 0 % si cheltuielile suplimentare ar creste cu 1 % deci profitul din fertilizarea porumbului ar scade cu 1 % .
3) Coloana ratei substituirii factorilor
0.351 Kg NPK / Ha porumb din cele 234 Kg NPK / Ha porumb au adus acelasi profit ca 1 Kg NPK / Ha grau din cei 251 Kg NPK / Ha .
1.022 Kg / Ha porumb crestere NPK fata de cele 234 kg NPK / Ha porumb si 1 Kg / Ha crestere NPK fata de cei 251 Kg NPK / Ha porumb ar scade profitul cu aceeasi suma.
2.91 % crestere NPK fata de cele 234 kg NPK / Ha porumb si 1 % crestere NPK fata de cei 251 Kg NPK / Ha grau , ar scade profitul cu acelasi numar de procente.
V. MAXIM DE VENIT CU CHELTUIELI LIMITATE(4230.5 lei)
Se realizeaza pentru x1= 116 Kg NPK / Ha grau si x2 = 167 Kg NPK / Ha porumb.
Rezulta productiile suplimentare maxime conditionate YS1 = 3390 Kg grau ; YS2 = 11691 Kg
Porumb ; venitul suplimentar maxim conditionat VS = 10218.1 lei ; cheltuielile suplimentare date
CS = 4230.5 lei din care CS1=1087.2 lei pentru fertilizarea graului si CS2 = 3143.4 lei pentru fertilizarea porumbului ; profitul suplimentar maxim conditionat PS = 5987.6 lei . Aceste valori se adaoga celor de la martor de la punctul a).
Productiile unitare totale sunt YUT1 = 2339 Kg grau / Ha si YUT2 = 3585 Kg porumb / Ha .
Cheltuielile unitare totale sunt CYT1 = 0.4184 lei cheltuieli / 1 Kg grau si CYT2 = 0.3005 lei cheltuieli / 1 Kg porumb .
Rata profitului total este RPT = 1.049 lei profit / 1 leu cheltuit .
Deoarece YUTi > YUi 0 , CYTi < CYi 0 si RPT > RP0 , merita sa folosim dozele maximului de venit cu cheltuieli limitate .
Tabel cu indicatorii economici ai maximului de venit cu cheltuieli limitate
|
Indicatori Economici |
Profit suplimentar |
Rata profitului suplimentar |
Rata Valorificare Factor |
||
|
Medii |
0.8107 lei |
1.5070 lei |
0.871 lei |
1.603 lei | |
|
Marginali |
0.6050 lei |
0.6202 lei |
0.662 lei |
0.700 lei | |
|
Elasticitati | |||||
COMENTARIU ASUPRA TABELULUI :
1) Coloana profitului suplimentar :
Fiecare din cele 116 Kg NPK / Ha grau a adus un profit suplimentar de 0.8107 lei.
Fiecare din cei 167 Kg NPK / Ha porumb a adus un profit suplimentar 1.5070 lei .
Al 117-lea Kg NPK / Ha grau ar creste profitul suplimentar cu valoarea de 0.6050 lei .
Al 168-lea Kg NPK / Ha porumb ar creste profitul suplimentar cu valoarea de 0.6202 lei .
Cresterea dozei de 116 Kg NPK / Ha grau cu inca 1 % ar creste profitul suplimentar
cu inca 0.75 % .
Cresterea dozei de 167 Kg NPK / Ha porumb cu inca 1 % ar creste profitul suplimentar
cu inca 0.41 % .
2) Coloana ratei profitului suplimentar :
Fiecare leu cheltuit cu fertilizarea chimica a graului din suma data de 1087.2 lei a adus un profit suplimentar de 0.871 lei.
Fiecare leu cheltuit cu fertilizarea chimica a porumbului din suma data de 3143.4 lei a adus un profit suplimentar de 1.603 lei.
Inca un leu cheltuit cu fertilizarea chimica a graului peste suma data de 1087.2 lei ar creste profitul suplimentar cu valoarea de 0.662 lei.
Inca un leu cheltuit cu fertilizarea chimica a porumbului peste suma de 3143.4 lei ar creste profitul suplimentar cu valoarea maxima de 0.700 lei.
Cresterea cheltuielilor cu fertilizarea chimica a griului cu inca 1 % peste suma de 1087.2 lei ar
creste profitul suplimentar cu inca 0.76 % .
Cresterea cheltuielilor cu fertilizarea chimica a porumbului cu inca 1 % peste suma de 3143.4 lei ar creste profitul suplimentar cu inca 0.44 % .
3) Coloana ratei substituirii factorilor
0.538 Kg NPK / Ha porumb din cele 167 Kg NPK / Ha porumb au adus acelasi profit ca 1 Kg NPK / Ha grau din cei 116 Kg NPK / Ha grau .
0.976 Kg / Ha crestere NPK fata de cele 167 Kg / Ha porumb si 1 Kg / Ha crestere NPK fata de cei 116 Kg NPK / Ha grau ar creste profitul cu aceeasi suma.
1.81 % crestere NPK fata de cei 167 Kg NPK / Ha porumb si 1 % crestere NPK fata de cei 116 Kg NPK / Ha grau , ar creste profitul cu acelasi numar de procente.
VI. MINIM DE CHELTUIELI CU VENIT GARANTAT(11370.5 lei)
Se realizeaza pentru x1= 164 Kg NPK / Ha grau si x2 = 186 Kg NPK / Ha porumb .
Rezulta productiile suplimentare date YS1 = 4448 Kg grau ; YS2 = 12430 Kg porumb ; venitul suplimentar dat VS = 11370.5 lei ; cheltuielile suplimentare minime conditionate CS = 5002.1 lei din care CS1 = 1515.1 lei pentru fertilizarea graului si CS2 = 3487 lei pentru fertilizarea porumbului ; profitul suplimentar maxim conditionat PS = 6368.3 lei . Aceste valori se adaoga celor de la martor de la punctul a).
Productiile unitare totale sunt YUT1 = 2445 Kg grau / Ha si YUT2 = 3622 Kg porumb / Ha .
Cheltuielile unitare totale sunt CYT1 = 0.4187 lei cheltuieli / 1 Kg grau si CYT2 = 3022 lei cheltuieli / 1 Kg porumb .
Rata profitului total este RPT = 1.037 lei profit / 1 leu cheltuit .
Deoarece YUTi > YUi 0 , CYTi < CYi 0 si RPT > RP0 , merita sa folosim dozele minimului de cheltuieli cu venit garantat .
Tabel cu indicatorii economici ai maximului de venit cu cheltuieli limitate
|
Indicatori Economici |
Profit suplimentar |
Rata profitului suplimentar |
Rata Valorificare Factor |
||
|
Medii |
0.7019 lei |
1.3953 lei |
0.761 lei |
1.496 lei | |
|
Marginali |
0.2389 lei |
0.2592 lei |
0.271 lei |
0.300 lei | |
|
Elasticitati | |||||
COMENTARIU ASUPRA TABELULUI :
1) Coloana profitului suplimentar :
Fiecare din cele 164 Kg NPK / Ha grau a adus un profit suplimentar de 0.7019 lei.
Fiecare din cele 186 Kg NPK / Ha porumb a adus un profit suplimentar 1.3953 lei .
Al 165-lea Kg NPK / Ha grau ar creste profitul suplimentar cu valoarea de 0.2389 lei .
Al 187-lea Kg NPK / Ha porumb ar creste profitul suplimentar cu valoarea de 0.2592 lei .
Cresterea dozei de 164 Kg NPK / Ha grau cu inca 1 % ar creste profitul suplimentar
cu inca 0.34 % .
Cresterea dozei de 186 Kg NPK / Ha porumb cu inca 1 % ar creste profitul suplimentar
cu inca 0.19 % .
2) Coloana ratei profitului suplimentar :
Fiecare leu cheltuit cu fertilizarea chimica a graului din suma minima de 1515.1 lei a adus un profit suplimentar de 0.761 lei.
Fiecare leu cheltuit cu fertilizarea chimica a porumbului din suma minima de 3487 lei a adus un profit suplimentar de 1.496 lei.
Inca un leu cheltuit cu fertilizarea chimica a graului peste suma minima de 1515.1 lei ar creste profitul suplimentar cu valoarea de 0.271 lei.
Inca un leu cheltuit cu fertilizarea chimica a porimbului peste suma minima de 3487 lei ar creste profitul suplimentar cu valoarea de 0.300 lei.
Cresterea cheltuielilor cu fertilizarea chimica a graului cu inca 1 % peste suma de 1515.1 lei ar
creste profitul suplimentar cu inca 0.36 % .
Cresterea cheltuielilor cu fertilizarea chimica a porumbului cu inca 1 % peste suma de 3487 lei ar creste profitul suplimentar cu inca 0.20 % .
3) Coloana ratei substituirii factorilor
0.503 Kg NPK / Ha grau din cei 186 Kg NPK / Ha grau au adus acelasi profit ca 1 Kg NPK / Ha grau din cei 164 Kg NPK / Ha grau .
0.922 Kg / Ha crestere NPK fata de cei 186 Kg NPK / Ha porumb si 1 Kg / Ha crestere NPK fata de cei 164 Kg NPK / Ha grau ar creste profitul cu aceeasi suma.
1.83 % crestere NPK fata de cei 186 Kg NPK / Ha porumb si 1 % crestere NPK fata de cei 164 Kg NPK / Ha grau , ar creste profitul cu acelasi numar de procente.
VII . Dozele de rentabilitate (cu profit nul)
Sunt x1 = 279 Kg NPK / Ha grau ; x2 = 304 Kg NPK / Ha porumb .
Modele cu restrictii liniare si functie-obiectiv patratica
In capitolul 6 am prezentat modele cu restrictii liniare si functii-obiectiv liniare .Ele au fost rezolvate prin imbunatatiri succesive ale unei solutii bazice initiale cu metoda simplex pana se ajunge la solutia bazica optima.
In sectiunea 2.1 punctele A si B , am prezentat doua modele cu o restrictie neliniara si functie-obiectiv cubica (venit maxim cu cheltuieli limitate si respectiv cheltuieli minime cu venit garantat) care au fost rezolvate cu metoda multiplicatorilor lui Lagrange.
In acesta sectiune vom prezenta un model intermediar cu restrictii liniare si functie-obiectiv patratica.
4.1 Cazul cand toate restrictiile sunt ecuatii
Modelul are forma :
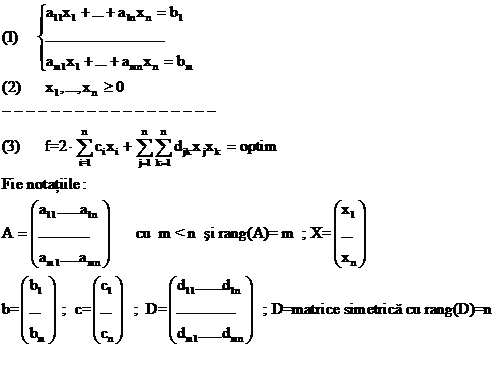
Modelul capata forma
matriciala :
A.X = b
X ≥ 0
f = 2.cT.X+XT.D.X = optim
Functia patratica f are punctul stationar X0 care anuleaza derivatele partiale de ordinul unu :
∂ f / ∂ x1 = 2.(c1 + d11x1 +.+ d1nxn ) = 0
∂ f / ∂ xn = 2.(cn + dn1x1 +.+ dnnxn ) = 0
adica matricial :
X0 = - D-1.c
X0 este punct de minim pentru f daca matricea D este pozitiv definita adica minorii ei principali sunt pozitivi :
![]()
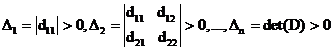
X0 este punct de maxim pentru f daca matricea D este negativ definita
adica minorii ei principali sunt negativi :
Δ1> 0 ; Δ2 < 0 ,., (-1)n.Δn > 0
X0 satisface restrictiile (4)+(5) daca A.X0 = b si X0 ≥ 0 deci daca :
A.D-1.c + b = 0 ; X0 ≥ 0
Exista cazurile :
I. Punctul stationar X0 = - D-1.c este punct de minim sau de maxim pentru f si verifica restrictiile (4) + (5) adica satisface relatia (8) .
In acest caz X0 este solutie optima pentru problema de optimizare (4) - (6).
II. Punctul stationar X0 fie nu este punct de minim sau de maxim pentru f ,
fie este punct de minim sau de maxim pentru f , dar nu verifica restrictiile
(4) + (5) deci nu satisface relatia (8).
In acest caz solutia optima a problemei de optimizare (4) - (6) , notata cu Xp , trebuie sa satisfaca restrictiile (4) + (5) deci este un vector pe frontiera multimii convexe a solutiilor pentru (4) + (5) (nu neaparat vector bazic pentru (4) + (5) ), pentru care f ia valoarea minima sau maxima .
Solutia optima Xp trebuie sa fie punct stationar pentru functia Lagrange:
L = 2.cT.X - XT.D.X - Y.(A.X / b)
unde Y = (y1,., ym)T este vectorul-coloana al multiplicatorilor Lagrange .
Conditia de punct stationar a lui Xp pentru L se scrie dupa transpunere :
(9) 2.c + 2.D.Xp - AT.Y = 0
A.Xp = b ; Xp ≥ 0
Din relatia (9) avem :
D.Xp = (1/2).AT.Y - c asa ca Xp = (1/2).D-1.AT.Y - D-1.c adica :
Xp = (1/2).D-1.AT.Y + X0
Relatia (10) devine : (1/2).A.D-1.AT.Y + A.X0 = b de unde :
Y = - 2.(A.D-1.AT)-1.(A.X0 - b)
Dupa aflarea lui X0 din relatia (7) , relatia (12) da vectorul-coloana Y al multiplicatorilor Lagrange y1,.,ym .
Relatia (11) devine :
Xp = X0 - D-1.AT.(A.D-1.AT)-1.(A.X0 b)
Dupa aflarea lui X0 din relatia (7) , relatia (13) da vectorul Xp al solutiei optime a modelului (4) - (6) .
Exemplu
Fie modelul cu restrictii liniare de tip ecuatii si functie-obiectiv patratica :
2x1+3x2+4x3 = 10
4x1+ x2+ 5x3 = 12
x1,x2,x3 ≥ 0
f = ( - 4x1 - 2x2 - 6x3 ) + ( x12 + x22 + x32 ) = minim
Se cere solutia optima a acestui model .
Solutie
Avem :
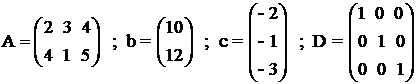
Matricea simetrica D este
pozitiv definita deci conform relatiei (7) functia f are punctul de minim :
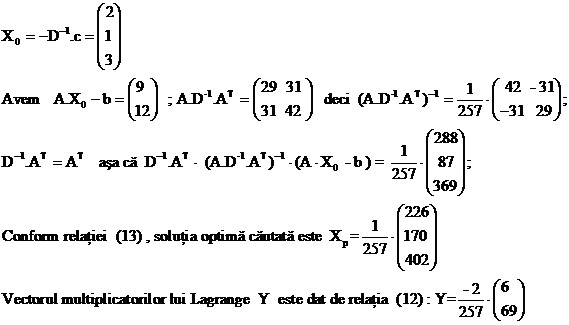
In concluzie , solutia optima Xp are componentele :
xp1=226 / 257 ; xp2 = 170 / 257 ; xp3 = 402 / 257
iar multiplicatorii Lagrange sunt : y1 = ( - 12 ) / 257 ; y2 = ( - 138) / 257
Valoarea minimului este f(Xp) = - 57
Restrictiile dau trei solutii bazice :
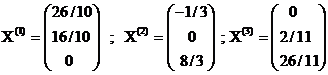
Avem Xp = α1.X(1) + α2.X(2) + α3.X(3) cu 0 ≤ αi ≤ 1 si α1 + α2 + α3 = 1
In cazul nostru avem α1=0.4134 ; α2 = 0.5866 ; α3 = 0 deci Xp se gaseste pe segmentul care uneste solutiile bazice(varfurile) X(1) si X(2) .
Cazul cand restrictiile sunt inecuatii
Fie problema de optimizare patratica :
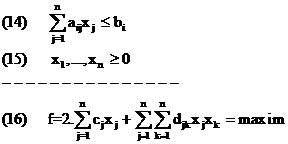
Se presupune ca matricea simetrica D=(dij) este de rang n si negativ definita deci functia f are un punct de maxim X0 = - D-1.c
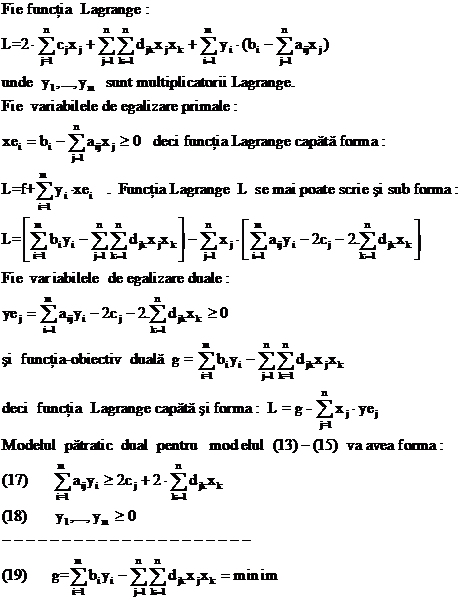
Pentru modelele patratice primal (14) - (16) si dual (17) - (19) ramane valabila teorema de dualitate din capitolul 2 .Si aici optimele primal si dual coincid : fmax = gmin
Ramane deasemenea valabila teorema ecarturilor complementare din capitolul 2 care exprima conditiile necesare si suficiente ca X,Y sa fie solutii optime pentru modelul patratic primal respectiv dual
(Conditiile Kuhn-Tucker) :
a) yi.xei = 0 (i=1,.,m)
b) xj.yej = 0 (j=1,.,n)
Fie modelul de optimizare patratica :
x1+x2 ≤ 3
4x1+x2 ≤ 4
x1 , x2 ≥ 0
----- ----- -----
f = (10x1+12x2)+(-0.5x12+0.1x1x2+0.1x2x1-0.4x22) = maxim
Modelul dual are forma :
y1+4y2 ≥ 10+( - x1+0.2x2)
y1+y2 ≥ 12+(0.2x1 - 0.8x2)
y1, y2 ≥ 0
g=(3y1+4y2) - (-0.5x12 + 0.1x1x2+0.1x2x1 - 0.4x22 )=minim
Problema primala din enunt se plaseaza in foaia EXCEL cu numele OPTIMP:
|
A1 |
B |
C |
D |
E |
F |
|
PROGRAM PATRATIC (OPTIMP) : |
|||||
|
RESTRICTII : |
|||||
|
COEF.X1 |
COEF.X2 |
MEMBRUL I |
MEMBRUL II | ||
|
FUNCTIA F: |
|||||
|
COEF.X1 |
COEF.X2 |
COEF. X1 |
COEF. X2^2 |
COEF. X1*X2 |
|
|
REZULTATE : |
|||||
|
VALOARE X1 |
VALOARE X2 |
VALOARE F | |||
FORMULE :
D5 : = $B$5*$B$12+$C$5*$C$12
D6 : = $B$6*$B$12+$C$6*$C$12
D12 : = B9*$D$12+C9*$C$12+D9*$B$12^2+E9*$C$12^2+F9*$B$12*$C$12
Se deschide meniul TOOLS (ALT T ) si se alege in feresatra TOOLS optiunea SOLVER . Apare
ferestra Solver parameters cu aspectul de mai jos :
In casuta din dreapta optiunii Set Target Cell se scrie adresa absoluta $D$12 in care se gasesc valorile succesive ale functiei-obiectiv f a problemei primale, ultima valoare fiind cea optima .
Sub aceasta casuta se face optiunea Max in butonul radio din stanga , deoarece problema primala este de maxim.
In casuta de sub optiunea By Changing Cells se dau adresele absolute $B$12 , $C$12 in care se gasesc valorile succesive ale variabilelor x1 , x2 , primele valori putand fi luate egale cu zero iar ultimele valori fiind cele optime.
Se activeaza optiunea Add care deschide fereastra Add Constraint in care se scriu cele doua restrictii ale problemei primale : $D$4 ≤ $E$4 ; $D$5 ≤ $E$5 dupa cum urmeaza :
int
bin
In fereastra Cell Reference se scrie membrul stang al restrictiei , din lista ascunsa de la mijloc se alege semnul restrictiei iar in fereastra Constraint se scrie membrul drept al restrictiei.
Dupa terminarea scrierii fiecarei restrictii , se activeaza optiunea Add pentru a introduce restrictia urmatoare.
Dupa inchiderea cu Ok a acestei ferestre , restrictiile precedente apar in casuta de sub optiunea Subject to the Constraints din ferestra Solver Parameters de mai sus .
Daca ulterior dorim sa modificam sau sa stergem unele restrictii , le selectam si folosim optiunile Change sau Delete ale ferestrei Solver Parameters.
Activand optiunea Solve din fereastra Solver Parameters , apare fereastra Solver results de mai jos :
In casuta de sub optiunea Reports selectam optiunile Answer , Sensitivity si Limits care vor atasa foii de calcul trei rapoarte cu rezultate : solutiile optime primala si duala , valoarea optimului si
intervalele pentru componentele vectorilor b si c , care nu necesita reoptimizare.
Dealtfel variabilele proprii x1 si x2 ale solutiei optime si valoarea optima a functiei-obiectiv f apar si in foaia EXCEL initiala in celulele $B$12 , $C$12 respectiv $D$12 .
Solutiile optime pentru modelele patratice primal si dual sunt :
|
Solutia optima primala |
Solutia optima duala |
|
I.Variabile primale proprii: X1=1/3 X2=8/3 |
III.Variabile duale de egalizare: ye1=0 ye2=0 |
|
II.Variabile primale de egalizare: Xe1=0 Xe2=0 |
IV.Variabile duale proprii: y1=886/90 y2=8/90 |
|
fmax=gmin=2935/90 |
|
|
Alocari → Restrictii ↓ |
NPK |
Apa |
SEMN |
LIMITE |
||
|
Grau |
Porumb |
Grau |
Porumb |
|||
|
X1(Kg/Ha) |
X2(Kg/Ha) |
X3(m3/Ha) |
X4(m3/Ha) |
|||
|
NPK - GRAU MAX |
300 Kg/Ha |
|||||
|
NPK - POR. MAX |
200 Kg/Ha |
|||||
|
APA - GRAU MAX |
1500 m3/Ha |
|||||
|
APA - POR.MAX |
2000 m3/Ha |
|||||
|
CHELTUIELI |
LEI /Ha |
Lei / Ha |
LEI / Ha |
LEI / Ha |
LEI / HA |
|
|
NPK |
40 Ha |
60 Ha |
15000 Kg |
|||
|
APA |
40 Ha |
60 Ha |
180000 m3 |
|||
|
PROD.SUPLIM. GRAU |
3 Kg GRAU / Kg NPK |
0.6 Kg GRAU / M3 APA |
1000 Kg/Ha |
|||
|
PROD.SUPLIM. PORUMB |
5 Kg Por. / Kg NPK |
0.9 Kg Por. / M3 APA |
1500 Kg/Ha |
|||
|
NPK - GRAU MIN |
80 Kg / Ha |
|||||
|
NPK - POR.MIN |
50 Kg / Ha |
|||||
|
APA - GRAU MIN |
500 M3/Ha |
|||||
|
APA - POR.MIN |
1000 M3/Ha |
|||||
|
PARTE LINIARA VENIT SUPLIM. |
LEI/Ha |
LEI/Ha |
LEI/Ha |
LEI/Ha |
MAXIM |
|
|
PARTE PATRATICA VENIT SUPLIM. | ||||||
Ca si in exemplul precedent , cu produsul informatic EXCEL , se obtin solutiile optime :
|
SOLUTIA OPTIMA PRIMALA |
SOLUTIA OPTIMA DUALA |
|
I.VPP(resurse alocate) X1=123.55 Kg NPK/Ha grau X2=115.70 Kg NPK/Ha porumb X3=1428.85 m3 Apa / Ha grau X4=2000 m3 Apa / Ha porumb |
III.VDP ye1=0 ye2=0 ye3=0 ye4=0 |
|
II.VPE(diferente intre resurse consumate si limite) xe1=176.45 Kg NPK/Ha grau deficit xe2=84.30 Kg NPK/Ha porumb deficit xe3=71.15 m3 Apa / Ha grau deficit →xe4=0 m3 Apa / Ha porumb deficit →xe5=0 lei necheltuiti xe6=3115.794 Kg NPK neconsumate xe7=2846.149 m3 apa neconsumati xe8=227.970 Kg Grau surplus xe9=878.503 Kg porumb surplus xe10=43.55 Kg NPK/Ha grau surplus xe11=65.70 Kg NPK/Ha porumb surplus xe12=928.85 m3 Apa / Ha grau surplus xe13=1000 m3 Apa / Ha porumb surplus |
IV.VDP y1=0 y2=0 y3=0 →y4=0.8577 →y5=0.0001 y6=0 y7=0 y8=0 y9=0 y10=0 y11=0 y12=0 y13=0 |
|
fmaxim = gminim = 872412.6 LEI |
|
Rezumat
In acest capitol se prezinta un model neliniar de alocare optima a resurselor in agricultura cu functii-obiectiv diferite : optim marginal , de echilibru , economic, tehnic , maxim de venit cu cheltuieli limitate , minim de cheltuieli cu venit garantat . Capitolul se incheie cu modele de optimizare cu restictii liniare si functie-obiectiv patratica .
Intrebari
Cum caracterizati optimul economic in alocarea de resurse ?
Cum caracterizati optimul tehnic in alocarea de resurse ?
Ce semnificatie au ratele substituirii factorilor in realizarea unui produs ?
Ce semnificatie au ratele valorificarii aceluiasi factor de catre produse diferite ?
Bibliografie
1. Stanasila O. " Analiza liniara si geometrie "Vol. I - II,Editura ALL ,2000 - 2001
2. Cenusa Gh. si col." Matematici pentru economisti " Editura CISON,2000
3. Cenusa Gh. si col." Matematici pentru economisti - culegere de probleme" Editura CISON,2000
4. Ene D. " Matematici (I) " Editura CERES , 2004
5. Gogonea S. , Ene D. " Analiza numerica " Editura Cartea Universitara , 2005
6. Ene D.,Gogonea S. "Metode numerice" Editura Cartea Universitara , 2005
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2243
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved