| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
| Navigatie |
NAVIGATIA COSTIERA
1. Erori in navigatia costiera
Navigatia costiera este domeniul navigatiei care studieaza metodele de determinare a pozitiei (punctului) navei, utilizand pentru aceasta parametrii masurati la repere la coasta (relevmente, distante, unghiuri orizontale si verticale, etc.).
Principiul fundamental al determinarii punctului navei cu metode costiere este acela ca punctul navei sa se gaseasca la intersectia a cel putin doua drepte (relevmente), arce, etc., trasate pe harta dupa anumiti parametri masurati la repere costiere.
In practica navigatiei insa, urmare a actiunii unei serii de factori, valorile masurate nu sunt niciodata cele adevarate, sunt deci eronate. Abaterii valorii masurate fata de valoarea reala a parametrului ce concura la determinarea punctului (relevment, distanta, s.a.) se numeste eroare.
Notiunea de eroare este inseparabil legata de notiunea de masurare (observare). Prin masurare (observare) se intelege operatiunea de comparare a marimii ce face obiectul masuratorii cu o alta, de aceeasi natura cu ea, considerata unitate sau etalon. In urma masuratorii se obtine un numar abstract care arata de cate ori marimea masurata este mai mare sau mai mica decat unitatea.
Orice observatie (masuratoare), indiferent de natura ei, este afectata de o eroare. Valoarea erorii poate fi mai mica sau mai mare, functie de o serie de factori, cum sunt:
precizia instrumentului utilizat pentru executarea masuratorii;
metoda utilizata;
experienta si capacitatile operatorului;
conditiile de mediu.
Orice eroare in masurarea parametrilor de navigatie implica o eroare in determinarea punctului navei, deci punctul determinat grafic, pe harta, nu este cel real, ci se poate afla mai aproape sau mai departe de cel real, functie de valoarea erorilor de masurare a parametrilor.
Definirea notiunii de eroare este necesara in navigatie pentru operatiunea de evaluare a preciziei punctului navei, care constituie un important indicator in aprecierea situatiei de navigatie si un factor de reducere a riscurilor; acesta operatiune se executa imediat dupa determinarea grafica, pe harta, a punctului navei.
Erorile care insotesc observatiile (masuratorile) parametrilor de navigatie, sunt:
erori grosiere;
erori sistematice;
erori accidentale.
Erorile grosiere sunt erori datorate unei neatentii a operatorului in procesul de masurare (de exemplu, erori de ordinul gradelor in masurarea unui relevment). Aceste erori sunt de cele mai multe ori cu un ordin de marime mai mari decat precizia aparatului cu care se executa masurarea; in consecinta ele pot fi detectate cu usurinta de catre operator si apoi indepartate.
In navigatie, atunci cand rezultatul masuratorilor este vadit eronat, se procedeaza la repetarea seriei de masuratori in vederea inlaturarii erorilor grosiere.
Erorile sistematice sunt erori a caror frecventa de aparitie se inscrie intr-o lege cunoscuta, ori care se poate determina. Ca urmare, influenta acestui tip de erori asupra observatiilor se poate anula prin introducerea de corectii. In navigatie, erorile sistematice sunt erorile instrumentale, adica erorile ramase in urma reglarii aparatelor de masura.
Erorile sistematice se inlatura astfel:
prin calcul, adaugand o corectie la valoarea masurata;
prin etalonarea corecta a aparatului de masura.
Erorile sistematice, acolo unde exista, se propaga cu aceasi cantitate si cu acelasi semn in toate valorile masurate cu acel instrument.
Erori accidentale sunt erori a caror valoare sau frecventa de aparitie nu se poate modela functie de anumite variabile independente; ele se supun doar legilor statistice.
Cauzele aparitiei erorilor accidentale sunt numeroase, si nu se poate prevedea in ce masura va actiona fiecare din aceste cauze. In general, actiunea erorilor accidentale este descrisa de urmatoarele legi:
a. Pentru o aceeasi valoare absoluta, erorile accidentale pozitive si negative au aceeasi frecventa de aparitie;
b. Valoarea modulului erorilor accidentale este invers proportionala cu valoarea probabilitatii de aparitie. Astfel, erorile accidentale cu valoare mare au probabilitate mica de aparitie, in timp ce erorile accidentale cu valoare mica, au frecventa mare de aparitie;
c. Pentru anumite conditii date, valoarea erorilor accidentale ce efectueaza masuratorile, nu poate depasi anumite valori limita;
d. Cand numarul observatiilor aceleeasi marimi tinde la infinit, media aritmetica a erorilor accidentale tinde la zero.
Actiunea erorilor accidentale se poate verifica, de exemplu, masurand o serie de n relevmente la un singur reper costier, cu nava in stationare. Se vor obtine n valori usor diferite intre ele, cu toate ca masuratorile s-au executat in aceleasi conditii, cu acelasi instrument, etc.
In practica, valoarea reala a marimii masurate nu se poate determina, insa se poate calcula cea mai probabila valoare a acesteia. Acest lucru se face pe baza postulatului lui Gauss, care stabileste ca media aritmetica a rezultatelor masuratorilor este cea mai probabila valoare a marimii cautate.
In practica, dupa determinarea valorii probabile a marimii masurate, este necesara evaluarea preciziei masuratorilor, care in navigatie se face prin calculul erorii medii patratice, avand in vedere faptul ca masuratorile se considera de egala precizie.
Erorile accidentale la care se face referire in postulatul Gauss nu au sens de actiune. in practica navigatiei insa, apar situatii cand erorile actioneaza pe o anumita directie; de exemplu, la masurarea unei distante la un reper costier erorile la masurarea distantei respective sunt distribuite intr-un sens sau altul in jurul unei valori medii, pe directia relevmentului la reperul respectiv (fig. 66):
|
|
[Fig 66] Eroarea vectoriala
Erorile caracterizate de o anumita directie de actiune pot fi reprezentate grafic printr-un vector.
Experienta a impus definirea unei erori de forma medie patratica, supusa postulatului Gauss, care sa caracterizeze intregul sistem de erori cu directie de actiune. Aceasta eroare, numita eroare vectoriala, este egala in modul cu eroarea medie patratica a masuratorilor, si este orientata pe directia rezultanta a actiunii acestora.
Eroarea vectoriala se noteaza cu s.
2. Linii de pozitie costiere
In navigatie si hidrografie, se executa curent operatiunea de determinare a pozitiei navei pe baza parametrilor masurati la repere costiere (distante, relevmente, unghiuri orizontale, unghiuri verticale, etc.). Toti acesti parametri sunt functii ce au ca argument coordonatele (j l ale punctului ce urmeaza a fi determinat.
Fie o functie reala u = f (j l ; se dau astfel de valori argumentelor j si l, incat valoarea lui u sa ramana constanta. Multimea perechilor (j l care respecta aceasta conditie, genereaza pe suprafata sferei terestre o izolinie sau o linie de pozitie. Altfel spus:
Linia de pozitie este locul geometric al punctelor (j l) de pe suprafata sferei din care se masoara acelasi parametru u=ct (relevment, distanta etc.) la un reper de navigatie (fig.66).
In virtutea acestei definitii, functia constanta u este chiar parametrul masurat, iar graficul acestei functii este linia de pozitie.
|
|
[Fig 67] Linii de pozitie
In navigatie se utilizeaza urmatoarele linii de pozitie:
Dreapta de relevment este locul geometric al punctelor din care se masoara acelasi relevment adevarat la un reper de navigatie.
Pe sfera terestra, acest loc geometric este o curba cu concavitatea spre pol, care trece prin punctul navei si prin reper, numita izoazimutala (fig.68a).
Datorita distantelor mici dintre nava si reper, aceasta curba se aproximeaza cu o dreapta, numita asa cum s-a precizat, dreapta de relevment. Modul de trasare a dreptei de relevment pe harta Mercator este aratat in fig. 68b.
|
|
|
|
[Fig 68a] Izolinia relevmentului |
[Fig 68b] Dreapta de relevment |
In cele ce urmeaza, se va face o distinctie neta intre notiunea de relevment (unghi in planul orizontului adevarat) si dreapta de relevment (linia de pozitie corespunzatoare relevmentului). Ofiterul de cart masoara o valoare de relevment cu alidada, iar pe harta va trasa dreapta de relevment corespunzatoare.
Dreapta de relevment este linia de pozitie de care se face uz cel mai frecvent in practica navigatiei costiere.
Arcul de cerc capabil de un unghi orizontal este locul geometric al punctelor din care se masoara aceeasi valoare de unghi orizontal (ao intre doua repere de navigatie (fig.69).
Se va face intotdeauna distinctie intre notiunea de unghi orizontal si notiunea de arc de cerc capabil de un unghi orizontal. Astfel, ofiterul de cart masoara cu sextantul un unghi orizontal αo intre doua repere de navigatie, si traseaza pe harta linia de pozitie corespunzatoare acestuia, adica arcul de cer capabil.
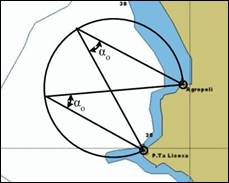
[Fig 69] Arcul de cerc capabil de un unghi orizontal
Pe harta Mercator, arcul de cerc capabil de un unghi orizontal trece intotdeauna prin cele doua repere la care s-a masurat unghiul orizontal; din oricare punct al arcului de cerc capabil sa masoare aceeasi valoare de unghi orizontal (αο) intre repere.
Cercul de distanta este locul geometric al punctelor egal departate de un reper de navigatie. Pe harta Mercator, acesta apare sub forma unui cerc cu centrul in reper, de raza egala cu distanta masurata de la nava la reper (fig. 70).
In consecinta, din oricare punct al cercului de distanta, se masoara aceeasi distanta la reperul de navigatie.
In mod analog, se va face distinctie intre notiunile de distanta si cerc de distanta. In navigatia costiera, ofiterul de cart masoara cu sextantul distanta la reperul costier, iar pe harta traseaza cercul de distanta corespunzator.
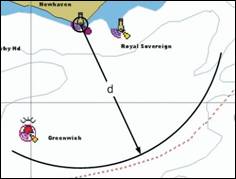
[Fig 70] Cercul de distanta
Izobata sau batimetrica este multimea punctelor avand aceeasi adancime a apei. Acestea apar pe harta de navigatie sub forma unor curbe neregulate, pe care este inscrisa valoarea adancimii (valoarea batimetrica), ca in fig.71.
[Fig 71] Batimetrica
Aliniamentul (fig.72) este dreapta determinata de doua repere. De regula, pe hartile marine sunt trasate aliniamente, pe care se inscrie valoarea relevmentului adevarat sau magnetic sub care aceste repere de navigatie se vad suprapuse.
[Fig 72] Aliniamentul
3. Eroarea medie patratica a punctului navei.
In navigatie, punctul navei se gaseste cel mai probabil la intersectia a cel putin doua linii de pozitie, corespunzand parametrilor de navigatie (Ra, d, ao av, etc.) masurati simultan la repere costiere.
Intereseaza nu numai coordonatele punctului determinat grafic pe harta, ci si gradul de incredere in acest punct, evaluat prin calculul erorii medii patratice in punctul navei.
Pentru calculul erorii medii patratice a punctului navei, este necesara evaluarea prealabila a preciziei de determinare a liniilor de pozitie. Aceasta se face prin calculul erorii medii patratice a fiecarei linii de pozitie ce concura la determinarea punctului.
Sunt date mai jos, in tabelul 1, valorile determinate statistic ale erorilor medii patratice ale liniilor de pozitie utilizate in navigatia costiera, numite uzual erori probabile:
|
Nr. crt |
PARAMETRUL DE NAVIGATIE |
EROAREA MEDIE PATRATICA |
|
Unghi orizontal masurat cu sextantul |
εO' = |
|
|
Unghi vertical masurat cu sextantul |
εV' = |
|
|
Drumuri si relevmente compas |
R |
|
|
Drumuri si relevmente giro |
R |
[Tabelul 1] Erori probabile
Cand conditiile meteo sunt nefavorabile, ori cand observatorul este neexperimentat, atunci valorile din tabelul 1 se vor mari proportional.
Valorile tabelate mai sus se utilizeaza in calculele de evaluare a preciziei determinarii punctului navei cu procedee costiere.
Eroarea medie patratica in masurarea (observarea) unui parametru de navigatie insumeaza erorile accidentale ale procesului de masurare, si are ca efect deplasarea izoliniei cu o cantitate proportionala cu modulul acestei erori; valoarea deplasarii grafice in ambele sensuri (fig.73) este materializata de eroarea vectoriala [s].
Pentru exemplificare, se considera ca un observator, plasat in punctul N(j l masoara Rg = 061 (CTG = +000 la reperul F (fig.73). Eroarea medie patratica (eroarea probabila) in masurarea relevmentului este de ε R Se converteste relevmentul (Ra = 062 si se traseaza pe harta prin reperul F. Eroarea probabila la ε R in masurarea relevmentului are ca efect deplasarea liniei de pozitie cu o cantitate proportionala cu ε R, egala cu eroarea vectoriala s. Sectorul hasurat din figura 73 se numeste culoar de nedeterminare si are semnificatia zonei cele mai probabile in care se poate gasi dreapta de relevment. Rezulta faptul ca latimea culoarului de nedeterminare (deci modulul erorii vectoriale) depinde de distanta nava-reper (d) si de eroarea probabila in masurarea relevmentului, deci:
s = εR d = εR d
Impartirea cu 573 s-a facut pentru compatibilizarea unitatilor de masura (convertirea in radiani a unghiului).
|
|
|
|
[Figura 73] Eroarea vectoriala. Culoarul de nedeterminare. |
[Figura 74] Eroarea medie patratica punctului navei |
Relatiile de calcul ale erorilor vectoriale ale liniilor de pozitie utilizate in navigatia costiera sunt:
|
LINIA DE POZITIE |
EROAREA VECTORIALA |
|
Dreapta de relevment |
S = ε R d / 57 |
|
Arcul de cerc capabil de un unghi orizontal |
S = (ε'0 d1 d2)/(3438' D) |
|
Cercul de distanta |
S = ε d |
[Tabelul 2]: Erori vectoriale
Observatie:Valorile lui ε se scot din tabelul 1. De asemenea, cu d s-au notat distantele de la nava la reper, iar cu D s-a notat distanta dintre repere.
La determinarea punctului cu doua linii de pozitii oarecare LP1 si LP2 corespunzatoare a doi parametri (de exemplu, relevmente giro) masurati simultan de la bordul navei de catre ofiterul de cart, erorile accidentale au ca efect deplasarea liniilor de pozitie cu cantitatile S1 si S2 (fig.74); punctul navei N se poate gasi oriunde in interiorul paralelogramului ABCD rezultat al intersectiei celor doua culoare de incertitudine. Paralelogramul ABCD se numeste paralelogramul erorilor.
Deplasarea maxima a punctului N este segmentul NB = ND, care se noteaza cu r si se numeste eroarea medie patratica a punctului navei. Se noteaza de asemenea cu q unghiul de intersectie a celor doua linii de pozitie.
Valoarea lui r se poate determina aplicand teorema cosinusului in triunghiul DGN:
DN = NG + DG - 2NGDGcos(180s - q
Se exprima NG si DG in triunghiurile dreptunghice NRG, respectiv GDH, se fac inlocuirile, si rezulta:
r = (S1 + S2) / sinq + 2S1S2cosq/sinq
Calculele de probabilitate au aratat faptul ca punctul navei, determinat la intersectia a doua linii de pozitie oarecare LP1 si LP2 se poate gasi in interiorul paralelogramului erorilor cu o probabilitate de 63,2%. Pastrand aceasta limita, termenul al II-lea al relatiei precedente se poate omite, rezultand:
r = cosecq ![]()
care reprezinta relatia generala de calcul a erorii medii patratice a punctului navei determinat la intersectia a doua linii de pozitie. Expresiile S1 si S2 se extrag din tabelul 2.
Omiterea termenului al II-lea al relatiei erorii medii patratice in punctul navei se traduce prin "taierea" colturilor paralelogramului erorilor, astfel ca acesta se poate aproxima cu un cerc, numit cerc al erorilor, a carui raza este eroarea medie patratica r
In practica, dupa determinarea grafica a punctului navei la intersectia liniilor de pozitie trasate pe harta (corespunzatoare celor doi parametri masurati simultan) se impune evaluarea preciziei punctului, deci a gradului de incredere in acesta. Se va proceda astfel:
se calculeaza raza cercului erorilor (r cu relatia dedusa mai sus (S1 si S2 se extrag din tabelul 2 iar q se scoate din harta);
se traseaza cercul erorilor de raza r cu centrul in punctul navei.
Nava se poate gasi in acest cerc cu o probabilitate de 63,2%. Pentru a asigura o probabilitate de 96% este necesar sa se dubleze raza cercului
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2984
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved