Corelatia statistica - Biostatistica

Corelatia statistica - Biostatistica

Notiunile dezvoltate in capitolele precedente ne-au permis sa studiem un caracter cantitativ dat: greutatea, inaltimea, tensiunea arteriala, intr-o populatie statistica determinata, definind parametrii numerici care permit sa caracterizam variatiile acestor marimi, sa precizam gradul de confidenta pe care il putem atasa rezultatelor si sa confruntam rezultatele cu cele obtinute pentru acelasi caracter cantitativ intr-o populatie statistica.

In stiintele experimentale si, in particular, in medicina si biologie, intereseaza nu numai variatia unei singure marimi, ci a doua valori, adica a doua caractere cantitative, intr-o populatie statistica. De exemplu, dorim sa stim daca exista intr-o grupa de subiecti o relatie intre greutate si inaltime, intre tensiunea arteriala si marimea umorala a unei substante, etc.

Pe plan matematic problema este rezolvata prin notiunea de functie, care traduce relatia intre variatia celor doua marimi. relatie materializata prin curba sa reprezentativa: y = f(x). In acest caz, unei valori date a variabilei independente x ii corespunde o valoare si numai una a variabilei dependente y, relatia y = f(x) permitand calcularea cu exactitate a acestei valori. O astfel de relatie fiind stabilita, cunoasterea unei valori ne este suficienta pentru determinarea valorii corespondente. Acest tip de relatie, numita relatie functionala, este cea care se intalneste in asa-zisele "stiinte exacte". Dar problema se complica atunci cand valorile care se studiaza (cea dependenta si cea independenta) sunt supuse fluctuatiilor.

Fluctuatiile se manifesta nu numai pentru o singura valoare data, ci pentru toate variabilele distributiei.

Exemplu:

Intr-un grup de subiecti carora li s-a studiat inaltimea si greutatea, pentru o valoare data a inaltimii (de exemplu 1.70 m) se va gasi seria tuturor subiectilor avand aceeasi inaltime si diferind intre ei prin greutate. Invers, pentru o valoare data a greutatii se va gasi seria subiectilor cu aceeasi greutate, dar cu inaltimi diferite. Nu se stie, si se pune problema daca greutatea este functie de inaltime, sau invers.

Se constata ca la o inaltime mica corespunde o greutate mai mica, si invers. Prin urmare, exista o relatie sigura intre aceste doua marimi, dar mai putin rigida decat relatia functionala propriu-zisa.

Aceasta relatie, de o natura particulara, constituie corelatia statistica, care joaca un rol important in stiintele vietii, si in particular in stiinta medicala, care este esentialmente o stiinta a corelatiei.

Procedee speciale ne permit sa studiem corelatia statistica, sa punem in evidenta legea generala care stabileste o legatura reciproca intre variatiile marimilor luate in studiu si sa apreciem cantitativ gradul, adica caracterul mai mult sau mai putin slab al acestei legaturi.

Ne vom limita la corelatia liniara, unde una dintre marimi variaza proportional cu alta.

1. Diagrama de dispersie

Un prim model de a aborda problema consta in a merge la reprezentarea grafica. Ca pentru a studia o functie, se merge la un sistem de axe rectangulare Ox si Oy, pe care se vor reprezenta valorile a doua marimi: x (inaltimea) si y (greutatea). Fiecare individ este reprezentat printr-o pereche (x, y).

Ansamblul populatiei studiate va fi reprezentat printr-un nor de puncte, care va constitui dispersia populatiei studiate (Figura 8.57).

Figura 8.57.Dispersia unei populatii (norul de puncte)

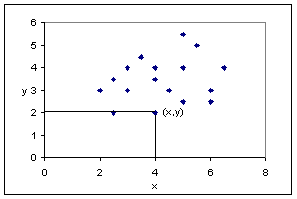
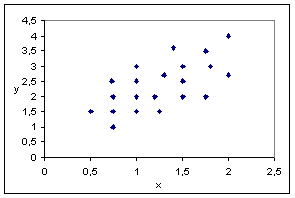
O astfel de diagrama, numita diagrama de dispersie, permite deja o aproximare a notiunii de corelatie: intr-adevar, daca exista o corelatie astfel incat, de exemplu, greutatile mai mari sa fie asociate inaltimilor mai mari, norul de puncte va avea o forma alungita oblic in sus si la dreapta (Figura 8.58). Daca, dimpotriva, se coreleaza valori mai mari ale uneia dintre marimi cu valori mai mici ale celeilalte, norul de puncte va avea un aspect analog, dar dirijat in jos si la dreapta (Figura 8.59).

Figura 8.58.Corelatie pozitiva

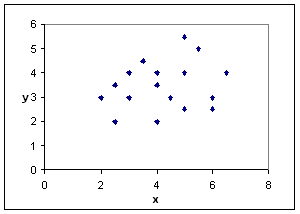
Atunci cand valorile nu se influenteaza reciproc, deci nu exista corelatie, norul de puncte va avea un aspect uniform dispersat (de exemplu, inaltimea si glicemia intr-un lot de persoane) - Figura 8.60. Absenta corelatiei indica independenta caracterelor studiate.

Figura 8.59.  Corelatie negativa (inversa)

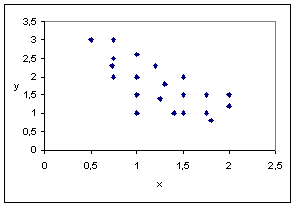
Figura 8.60: Corelatie zero

2. Notiunea de covarianta

Putem considera o sub-populatie a unei populatii date, careia ii vom calcula:

media ;

abaterea de la medie ;

media ;

abaterea de la medie .

Fie = punctul central al diagramei (centrul de greutate al norului de puncte) - Figura 8.61.

Trasam prin doua noi axe de coordonate, Mx¢ si My¢, paralele cu axele initiale Ox si Oy. Aceste axe impart planul in 4 zone:

in zona din dreapta-sus (cadranul I), abaterile de la medie ale ambelor variabile sunt pozitive: . Prin urmare, si produsul lor va fi pozitiv: .

in zona din stanga-jos (cadranul III), abaterile de la medie ale ambelor variabile sunt negative: . Prin urmare, produsul lor va fi tot pozitiv: .

in zona din dreapta-jos (cadranul II), abaterea de la medie pentru x va fi pozitiva, , iar abaterea de la medie pentru y va fi negativa, . Prin urmare, produsul lor va fi negativ: .

in zona din stanga-sus (cadranul IV), abaterea de la medie pentru y va fi pozitiva, , iar abaterea de la medie pentru x va fi negativa, . Prin urmare, produsul lor va fi negativ: .

Figura 8.61. Centrul de greutate al norului de puncte si impartirea planului in cadrane

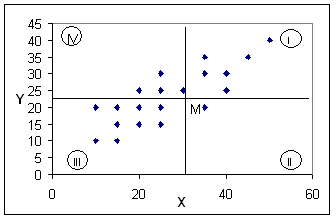
Daca exista o corelatie pozitiva intre x si y, majoritatea punctelor trebuie sa se gaseasca in cadranele I si III. In consecinta, daca calculam pentru fiecare pereche de valori (x, y) produsul si facem suma algebrica a tuturor acestor produse, obtinem ca:

.

In cazul corelatiei negative, majoritatea punctelor norului se vor situa in cadranele II si IV; analog, pentru fiecare pereche de valori (x, y) produsul si facand suma algebrica a acestor produse, obtinem ca:

Daca nu exista corelatie, punctele vor fi egal repartizate in cele patru cadrane si deci, urmand un rationament analog:

Pentru a da o semnificatie mai generala acestei sume, o raportam la numarul de cazuri N. Definim astfel notiunea de covarianta, P:

Deoarece : deviatia standard traduce dispersia statistica in cazul unei singure serii statistice.

3. Linia de regresie

Regresia este o metoda de estimare a relatiei numerice dintre variabile. Numele de "regresie" se datoreaza lui Galton (1886), care a dezvoltat tehnicile de investigare a relatiei dintre inaltimea copiilor si a parintilor lor. In problemele de regresie, scopul este sa vedem cat de bine poate fi folosita o variabila pentru a o predictiona pe cealalta.

Figura 8.62:  Linia de regresie a lui y in x

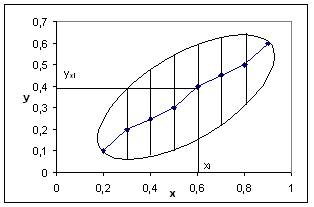
Cand studiem o serie statistica importanta, avem interesul sa grupam valorile in clase. Putem proceda la fel pentru distributia tuturor valorilor lui x. Prin urmare, vom decupa norul de puncte in bezi verticale (Figura 8.62).

Vom nota toate valorile lui y care corespund valorilor lui x din aceeasi clasa, si vom calcula valorile medii pentru acest y.

Pentru fiecare banda verticala a norului de puncte se obtine astfel un numar sigur de valori medii pentru y, numite punctele mediane ale fiecarei clase. Unind aceste puncte obtinem linia de regresie, sau linia de estimare a lui y in x.

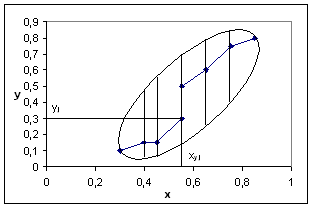
Bineinteles, putem, invers, sa il estimam pe x in functie de y. Pentru aceasta, este suficient sa plecam de la y si sa partajam norul de puncte in benzi orizontale, corespunzatoare fiecareia dintre clasele individualizate pe axa Oy (Figura 8.63). Valorile medii ale lui x obtinute in fiecare dintre aceste benzi orizontale permit sa definim o linie de regresie a lui x in y, evident diferita de cea precedenta.

Liniile de regresie dau imaginea variatiilor mediilor unei marimi in functie de alta. Ele exprima legea generala, care stabileste variatiile acestor doua marimi, fiind echivalentul curbei reprezentative a unei functii. Ele permit ca, plecand de la o marime variabila numita variabila de control, sau explicativa (care joaca rolul variabilei independente), sa obtinem informatii despre alta variabila, numita variabila controlata, sau explicata (care joaca rolul variabilei dependente, sau al functiei).

Figura 8.63:  Linia de regresie a lui x in y

Exemplu:

Daca y este greutatea si x este inaltimea, linia de exprimare a lui y functie de x va indica greutatea medie y corespunzatoare unie inaltimi date x, exact la fel ca si cum aceasta greutate medie ar fi fost o functie de inaltime.

4. Dreapta de regresie

Unul dintre cazurile cele mai interesante in practica este acela unde legea variatiilor mediilor, reprezentata prin linia de regresie, este o lege liniara, adica o marime variaza proportional cu cealalta.

In acest caz, linia de regresie este o dreapta a carei liniaritate este mai putin mascata de fluctuatiile de esantionaj. Deci vom incerca sa ajustam linia franta de regresie obtinuta experimental la o dreapta teoretica, numita dreapta de regresie, sau dreapta de estimare, ceea ce revine la a verifica legitimitatea acestei asimilari. Se poate trasa aceasta dreapta din ochi, dar numai in cazul in care forma norului este deja bine definita, si cand avem mai putine puncte; procedeul, insa, este putin precis.

Metoda generala adoptata este metoda celor mai mici patrate.

Dreapta obtinuta trebuie sa dea cea mai buna estimare a unei variabile functie de alta. De exemplu, pentru dreapta de estimare a lui y, trebuie sa gasim dreapta care, pentru o valoare data a lui x, furnizeaza cea mai buna estimare pentru y, adica aceea pentru care valorile lui y vor fi cel mai putin dispersate posibil.

Fie d distantele verticale (numite reziduuri) ale diferitelor puncte ale diagramei dreptei D (Figura 8.64). Aceste reziduuri formeaza o distributie cu media d si dispersia S_d².

Din toate dreptele posibile, cea mai buna va fi cea pentru care dispersia S_d², adica suma patratelor distantelor punctelor diagramei la dreapta, este minima (de unde numele metodei). Aceasta conditie implica faptul ca dreapta va trece prin punctul central al diagramei, iar suma reziduurilor de o parte a dreptei este egala cu suma reziduurilor de cealalta parte a dreptei.

Se arata ca dreapta care corespunde acestor conditii are ecuatia:

, unde .

Fie P (Figura 8.65) un punct al diagramei si urmatoarele elemente:

x, y coordonatele sale in raport cu axele Ox, Oy;

, coordonatele in raport cu axele Mx', My';

A, punctul de pe D situat pe verticala trecand prin P;

X, Y coordonatele lui A in raport cu axele Ox, Oy;

a = tg(a , panta dreptei D.

In triunghiul MAB avem:

.

Din figura se vede ca

Aceasta reprezinta ecuatia unei drepte trecand prin doua puncte (A si M), adica dreapta D.

Din figura se vede si ca:

d = PA = PB - AB = y' - ax'

Þ .

Acest trinom in a trece printr-un minim cand derivata sa se anuleaza:

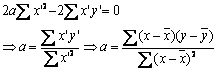
Se definesc astfel coeficientii liniari de regresie:

a_x : coeficientul liniar de regresie al lui y in x, care masoara panta dreptei D pe orizontala Ox. Indica de cate ori in medie y este mai mare sau mai mic decat x. Este pozitiv sau negativ dupa cum dreapta este ascendenta sau descendenta de la stanga la dreapta.

In mod simetric (schimband x cu y si y cu x) se defineste dreapta de regresie a lui x in y, care corespunde ecuatiei:

, cu coeficientul de regresie corespunzator a_y. Prin urmare, avem si:

- a_y : coeficientul liniar de regresie al lui x in y, care masoara panta dreptei D pe verticala Oy. Indica de cate ori x este mai mare sau mai mic decat y. 

Formulele coeficientilor liniari de regresie arata ca ei se pot exprima la fel de bine si in functie de covarianta P

5. Dreapta de regresie si corelatia liniara

Dreptele de regresie permit de a preciza mai mult notiunea de corelatie liniara.

Exista o corelatie perfecta, cazul relatiei functionale unde unei valori date x ii corespunde o valoare si numai una y si invers, unei valori date y ii corespunde o unica valoare a lui x. Dreapta de regresie a lui y functie de x, D_y este identica cu dreapta de regresie a lui x functie de y, D_x; cele doua drepte D_x si D_y se suprapun intr-o unica linie, care exprima relatia directa de proportionalitate intre variatiile celor doua marimi (Figura 8.66).

Daca nu exista corelatie intre variatiile celor doua marimi, valoarea medie a lui y va fi independenta de valoarea lui x; aceasta valoare va fi aceeasi pentru orice valori ale lui x, si prin urmare dreapta D_y de regresie a lui y in x este paralela cu axa Ox. Analog, valoarea medie a lui x este independenta de valorile lui y, iar dreapta D_x de regresie a lui x in functie de y va fi paralela cu axa Oy; prin urmare, cele doua drepte D_x si D_y sunt perpendiculare (Figura 8.67).

			Figura 8.66.  Cazul corelatiei perfecte

			Figura 8.67:  Cazul corelatiei zero

Intre aceste doua extreme se situeaza cazul in care exista corelatie; atunci exista doua drepte de regresie D_x si D_y care formeaza intre ele un unghi < 90⁰ (Figura 8.68). In consecinta, daca se parcurg toate valorile lui r, se observa ca cele doua drepte de regresie se rotesc in jurul punctului M, apropiindu-se una de cealalta, pana cand se vor confunda (cazul corelatiei perfecte).

Convergenta sau divergenta acestor doua drepte da un aspect vizual gradului de legatura intre cele doua variabile, aceasta legatura fiind cu atat mai stransa cu cat cele doua drepte sunt mai apropiate. Se va putea deci evalua cantitativ gradul de corelatie, cu conditia de a gasi un parametru care sa dea pozitia celor doua drepte. Se deduce ca in parametru vor fi implicate pantele celor doua drepte.

	Figura 8.68. Cazul corelatiei uzuale

6. Coeficientul de corelatie liniar

Se utilizeaza ca parametru de corelatie produsul (media geometrica a celor doua pante de regresie); acest parametru se numeste coeficientul corelatiei liniare.

O alta formula de calcul al coeficientului de corelatie liniara rezulta din:

Prin urmare, r reprezinta covarianta P atunci cand cele doua serii de variabile sunt raportate la abaterile tip, s_x si s_y

Aceasta formula permite sa exprimam pantele a_x si a_y functie de r:

.

Folosind aceste formule, este posibil sa studiem natura corelatiei:

cand nu exista corelatie: ;

cand exista corelatie perfecta: ; apar doua situatii:

r = + 1 : indica o corelatie perfecta pozitiva (Figura 8.69);

r 1 : indica o corelatie perfecta negativa (Figura 8.70).

Studiul parametrului r permite deci o evaluare cantitativa a corelatiei.

7. Principiul de calcul al unui coeficient de corelatie liniara

Pentru calculul unui coeficient de corelatie liniara, se aplica formula:

Este necesar sa se calculeze covarianta P si abaterile tip s_x si s_y ale distributiei. Daca datele nu sunt prea numeroase, se pot calcula direct aceste elemente care intra in formula coeficientului de corelatie.

Exemplu:

Ne propunem sa evaluam corelatia pe 40 subiecti pentru care vom inregistra greutatea (x) in kilograme si marimea corticoizilor urinari y, in mg/24h. Rezultatele obtinute sunt indicate in tabelul

Tabelul 8.9: Corticoizii urinari si greutatea

Vor fi utilizate urmatoarele formule simplificate:

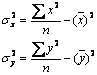
Covarianta va fi:

Deoarece , covarianta devine:

.

Dar

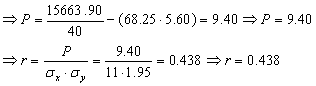
Exista deci o corelatie neta intre greutate si marimea corticoizilor urinari. Vom putea calcula ecuatia dreptei de regresie: coeficientul liniar al regresie este .

Ecuatia dreptei de regresie va fi:

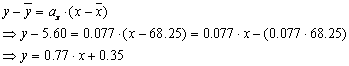
Aceasta dreapta trece prin punctul central al diagramei, ; ordonata la origine este x₀ = 0, y₀ = 0.35.

Invers, pentru o femeie de 60 kg, corticoizii vor fi

y x

5 mg/24 h.

Intr-un esantion suficient de mare, pentru coeficientul de corelatie se arata ca distributia de esantionaj poate fi considerata practic normala in jurul valorii estimate r_e, care a fost gasita in esantion, cu abaterea standard S_r.

n = nr. de cupluri de valori (x, y).

Intervalul de confidenta al coeficientului este deci:

r_e S_r, cu un coeficient de securitate de 95% si

r_e S_r, cu un coeficient de securitate de 99%.

8. Corelatia semnificativa diferita de zero

In cele mai multe cazuri, in biologie se doreste sa se stie daca exista sau nu o corelatie intre doua fenomene studiate. Inainte de a admite ca, intr-o populatie de doua serii de valori unde corelatia este nula, coeficientul de corelatie este distribuit normal in jurul lui zero cu o eroare standard,

, care reprezinta valoarea lui S_r, pentru r = 0.

Vom putea spune ca valoarea r_e gasita pentru r este semnificativ diferita de zero si r_e este superioara lui 2 S₀, adica cu un prag de semnificatie de 95% si lui 2.6 S₀, adica cu un prag de securitate de 99%.

Pentru coeficientul de corelatie r = 0.471 avem:

95%: = 0.122

99%: = 0.159

Pentru esantioane cu N £ 100, rationamentul anterior nu este valabil. Fisher a stabilit tabele care dau, in functie de N (mai precis in functie de gradul de libertate) valorile corespunzatoare ale lui 2 S₀ si ale lui 2.6 S₀.

Exemplu:

Verificam daca coeficientul de corelatie r = 0.438 gasit este inalt semnificativ diferit de zero.

Pentru g = n - 2 = 40 - 2 = 38, tabelul indica:

Þ

Þ

Deci coeficientul gasit este semnificativ la un prag de semnificatie de 99%.

9. Eroarea standard de estimare

Dreapta de regresie exprima doar tendinta centrala a estimarii variabilei corespunzatoare y ( de exemplu, dreapta de estimare a lui y functie de x).

Dispersia de estimare este reprezentata de abaterile punctelor diagramei in raport cu dreapta de regresie corespunzatoare. Mai precis, ea va fi evaluata prin suma, raportata la N, a patratelor abaterilor d ale dreptei de regresie a lui y, adica prin dispersia reziduurilor in raport cu dreapta de estimare a lui y, notata cu .

Se arata ca . Prin urmare,

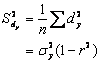
Deci avem:

va fi abaterea standard a distributiei reziduurilor in raport cu dreapta D. Daca admitem ca distributia este gaussiana, trasand doua paralele le dreapta D, situate la o distanta egala cu (masurata vertical), de o parte si de alta a dreptei D, va trebui ca aceasta suprafata sa inglobeze 68% din date, adica punctele diagramei de distributie (Figura 8.71).

Aceasta abatere standard de regresie a lui y este adesea utilizata pentru a vizualiza limitele estimarii unei variabile plecand de la dreapta de regresie corespunzatoare.

Formula lui arata ca este cu atat mai mic, cu cat banda determinata este mai ingusta (r²

Pentru r² = 1 Þ r = 1, urmeaza ca = 0, deci banda se reduce la o linie, aceasta fiind grosimea corelatiei perfecte.