Criptografia (Sisteme informatice)

Criptografia

(Sisteme informatice)

Cuprins

Bazele criptografiei..

Cifruri de substitutie monoalfabetica..................4

Cifruri de substitutie polialfabetice.5

Metoda Kasiski..7

Indexul de coincidenta8

Substitutia "perfecta..

Bloc notes-ul........................9

Siruri de numere aleatoare mari.9

Cifrul Vernam.......................10

Cifrul Vernam binar..10

Criptofrafia moderana

Cifrurile simetrice..11

Algoritmul DES..12

Algoritmul AES

Algoritmul Lucifer......................15

Algoritmul Blowfish......................16

Cifrurile asimetrice (cu chei publice)..17

Algoritmul Merkle-Hellman17

Algoritmul IDEA.....................18

Algoritmul Rivest-Shamir-Adelman.18

Problema autentificarii.....................

Problema modificarii mesajelor................

Bazele criptografiei

Definitia criptografiei pleaca de la etimologia cuvantului cripto care vine din grecescul kryptos, care inseamna ascuns, obscur, secret, iar grafie de la graphia, adica scriere. O definitie concisa a termenului este data de Yaman Akdeniz, in articolul sau "Cryptography and Encryption":"Criptografia, definita ca <stiinta care se ocupa cu studiul scrierii secrete>, trateaza mijloacele prin care comunicatiile si datele pot fi codificate pentru a preveni descoperirea lor prin interceptare, folosind coduri, cifruri si alte metode, astfel incat numai anumite persoane sa poata vizualiza mesajul initial"

Primele mentionari despre criptografie apar acum 4000 de ani in Egiptul antic.

In India, nu mult dupa ce scrisul a fost inventat, se pomeneste de scriere secreta; Kama Sutra , unde scrisul secret este pe lista lucrurilor pe care trebuie sa le stie o femeie. Arabii, in al 7-lea secol i.e.n., au fost primii care au scris despre metode de criptanaliza. Istoricii au descoperit un text folosit in magie datat in jurul anului 855 i.e.n. Detalii interesante din istoria criptografiei le gasim in cartea lui David Kahn.

Include criptografia si criptanaliza[2].

Criptografia sau stiinta codificarii informatiei in vederea impiedicarii acceselor neautorizate, are o lunga istorie, confidentialitatea comunicarii fiind o cerinta a tuturor timpurilor. Daca ar trebui sa alegem un singur exemplu al criptografiei 'clasice', acesta ar fi cifrul lui Cezar, nu atat datorita celebritatii imparatului roman de care se leaga folosirea lui, ci pentru ca principiul sau de baza s-a mentinut nealterat aproape doua milenii. Dar iata care este acest principiu! Cifrarea este bazata pe o substitutie a fiecarui simbol al mesajului cu un altul, aflat in alfabet la trei pozitii dupa el. In felul acesta, celebrele cuvinte VENI VIDI VICI transmise de Cezar lui Matius, dupa victoria de la Zela asupra lui Farnace (anul 47 i.e.n.), ar putea fi codificate prin YHQL YLGL YLFL. Pentru a putea descifra mesajul, procedeul de cifrare se inverseaza, fiecare litera fiind inlocuita cu una aflata cu trei pozitii inaintea sa in alfabet.

Caesar folosea o deplasare de 3 pozitii, astfel incat litera p_i din text clar era criptata ca litera c_i din textul cifrat prin regula: c_i=E(p_i)=p_i+3.

O tabela completa de translatie a cifrului Caesar este:

Alfabetul clar:  ABCDEFGHIJKLMNOPQRSTUVWXYZ

Alfabetul cifrat: defghijklmnopqrstuvwxyzabc

Primele cifruri trebuiau sa fie simple si usor de folosit. Orice cifru care era suficient de complicat incat algoritmul sau trebuia sa fie transmis in scris, risca sa fie descoperit daca interceptorul captura mesagerul cu respectivele instructiuni scrise. Cifrul lui Caesar este un cifru extrem de simplu. Regula p_i+3 era usor de memorat; expeditorul putea sa-si noteze pe loc tabela de translatie, sa codifice mesajul de transmis si apoi sa distruga hartia continand cifrul. Aceasta regula este insa si cea mai mare slabiciune a cifrului Caesar. O criptare sigura nu trebuie sa permita interceptorului ca, dintr-o cantitate mica de informatii sa poata sa deduca regula de criptare.

In orice limba, cuvintele de doua sau trei litere sunt relativ putine. Astfel, un atac consta in substituirea cuvintelor scurte cunoscute din textul cifrat si incercarea de a substitui caracterele care mai apar in alte locuri in text. Facand mai multe incercari si verificand daca textul decodificat are vreun inteles se va putea decripta mesajul.

Acest gen de criptanaliza este unul ad hoc, bazat pe deductie si incercare. O alta abordare este considerarea literelor comune pentru inceputul cuvintelor, sfarsitul cuvintelor sau care prefixe sau sufixe sunt cele mai folosite in limba respectiva, conform unor liste publicate si folosite de catre criptanalisti.

Sistemul de criptare folosit de Caesar este unul ce are la baza substitutia monoalfabetica.

In substitutiile monoalfabetice, alfabetul este amestecat si fiecare litera din textul clar corespunde unei litere unice din textul cifrat. Permutare este o reordonare a elementelor unei multimi. Doua exemple de permutari ale multimii formate din numerele de la 1 la 10 sunt: p = si p =. O permutare este o functie, astfel incat se poate scrie p (3)=5 sau p (7)=4. Daca a₁, a₂, , a_k sunt literele unui alfabet de text clar si p este o permutare a multimii , intr-o substitutie monoalfabetica avem. De exemplu, p(a) poate fi functia p(a)= 25-a, astfel incat A va fi codificat ca A, B ca Y, si Z va fi reprezentat ca A. Totusi, fiecare pereche de litere text clar - text cifrat comunica in ambele sensuri: p(F)=u si p(U)=f. Aceasta dubla corespondenta ofera un ajutor suplimentar interceptorului.

O alternativa este folosirea unei chei, un cuvant care controleaza criptarea. Daca acest cuvant este cifru, expeditorul sau destinatarul mai intai scrie alfabetul si apoi scrie cheia sub primele litere ale alfabetului, continuand cu literele ramase intr-o ordine usor de memorat.

Alfabetul clar:  ABCDEFGHIJKLMNOPQRSTUVWXYZ

Alfabetul cifrat  cifruabdeghjklmnopqstvwxzy

Spre sfarsitul alfabetului inlocuirile sunt din ce in ce mai apropiate si ultimele sapte caractere isi corespund. Deoarece literele de la sfarsitul alfabetului sunt dintre cele mai rar folosite, aceasta expunere nu este totusi de un mare ajutor interceptorului Un cifru este mai sigur din punct de vedere criptografic daca prezinta o distributie cat mai regulata, care sa nu ofere informatii criptanalistului.

O alta cale de a aplatiza distributia este combinarea distributiilor ridicate cu cele scazute cifruri de substitutie polialfabetice)

Daca T este criptat cateodata ca a si alta data ca b, si daca X este de asemenea cateodata criptat ca a si alta data ca b, frecventa ridicata a lui T se combina cu frecventa scazuta a lui X producand o distributie mai moderata pentru a si pentru b.

Doua distributii se pot combina prin folosirea a doua alfabete separate de criptare, primul pentru caracterele aflate pe pozitii pare in text clar, al doilea pentru caracterele aflate pe pozitii impare rezultand necesitatea de a folosi alternativ doua tabele de translatare. Tehnica celor doua permutari poate conduce si la cazul nedorit al unei coliziuni accidentale a doua litere de frecventa scazuta, sau a doua litere de frecventa ridicata

O alta abordare este extinderea numarului de permutari. Extensia maxima este de 26 de permutari, astfel incat o litera din text poate fi criptata ca orice litera din textul cifrat.

2

01234567890123456789012345

abcdefghijklmnopqrstuvwxyz

A abcdefghijklmnopqrstuvwxyz 0

B bcdefghijklmnopqrstuvwxyza 1

C cdefghijklmnopqrstuvwxyzab 2

D defghijklmnopqrstuvwxyzabc 3

E efghijklmnopqrstuvwxyzabcd 4

F fghijklmnopqrstuvwxyzabcde 5

G ghijklmnopqrstuvwxyzabcdef 6

H hijklmnopqrstuvwxyzabcdefg 7

I ijklmnopqrstuvwxyzabcdefgh 8

J jklmnopqrstuvwxyzabcdefghi 9

K klmnopqrstuvwxyzabcdefghij 10

L lmnopqrstuvwxyzabcdefghijk 11

M mnopqrstuvwxyzabcdefghijkl 12

N nopqrstuvwxyzabcdefghijklm 13

O opqrstuvwxyzabcdefghijklmn 14

P pqrstuvwxyzabcdefghijklmno 15

Q qrstuvwxyzabcdefghijklmnop 16

R rstuvwxyzabcdefghijklmnopq 17

S stuvwxyzabcdefghijklmnopqr 18

T tuvwxyzabcdefghijklmnopqrs 19

U uvwxyzabcdefghijklmnopqrst 20

V vwxyzabcdefghijklmnopqrstu 21

W wxyzabcdefghijklmnopqrstuv 22

X xyzabcdefghijklmnopqrstuvw 23

Y yzabcdefghijklmnopqrstuvwx 24

Z zabcdefghijklmnopqrstuvwxy 25

Se stabileste care este coloana care urmeaza a fi folosita este principalul dezavantaj al rotatiei celor 26 de permutari, care poate fi insa evitat prin folosirea unui cuvant cheie. Literele acestuia vor selecta coloanele pentru criptare

Substitutiile polialfabetice sunt, aparent, mai sigure decat cele monoalfabetice.

In literatura criptografica sunt prezentate doua metode puternice care pot decripta mesaje scrise chiar folosind un numar mare de alfabete si anume, metoda Kasiski[3] si metoda indexului de coincidenta.

Metoda Kasiski

Metoda Kasiski, numita astfel dupa ofiterul prusac care a dezvoltat-o, este o cale de a gasi numarul alfabetelor care au fost folosite la criptare.

Metoda se bazeaza din nou pe aspectul de regularitate al limbii. In texte se repeta nu numai litere, dar de asemenea grupuri de litere sau cuvinte intregi.

Metoda Kasiski -daca un mesaj este codificat cu n alfabete in rotatie ciclica si un cuvant particular, sau un grup de litere apare de k ori in textul clar, el va fi codificat de aproximativ k/n ori cu acelasi alfabet. De exemplu, daca cuvantul cheie are sase litere, exista doar sase feluri diferite de a pozitiona cuvantul cheie deasupra unui cuvant din text clar. Un cuvant care apare in text de mai mult de sase ori va fi criptat de cel putin doua ori identic.

Pentru a folosi metoda Kasiski, se identifica in text cifrat toate formele care se repeta. Formele repetitive scurte, cum ar fi grupurile de cate doua litere, se ignora. Orice forma care contine mai mult de trei litere este luata in considerare (probabilitatea ca doua secvente de cate patru litere sa nu apartina aceluiasi segment in text clar este de 0,0000021).

abcdefabcdefabcdefabcdefabcdefabc

crypto is short for cryptography

"crypto' este grupul, iar distanta dintre grupari este de 20 de cararctere. Pentru fiecare aparitie a formei se marcheaza pozitia de start; apoi se calculeaza distanta dintre pozitiile de start succesive

O alta metoda de criptanaliza estimeaza cat de bine se potriveste o anumita distributie cu distributia literelor in limba in care a fost scris mesajul in text clar. Indexul de coincidenta este o masura a variatiei dintre frecvente intr-o distributie.

Indexul de coincidenta

Indexul de coincidenta este o masura pe baza careia se va determina numarul de alfabete care s-au folosit la criptare

Mesajul in text clar este caracterizat de distributia de limba. Notam cu Pb_a probabilitatea ca o litera aleasa aleator din mesajul in text clar sa fie a, Pb_b sa fie b,, Pb_z sa fie z.

Pb_a + Pb_b + + Pb_z = Pb_i = 1.

O distributie perfect plata, uniforma, se caracterizeaza prin faptul ca toate literele au aceeasi probabilitate de aparitie:

Pb_a = Pb_b = = Pb_z =

Graficul unei astfel de distributii este o linie orizontala. Pentru o distributie oarecare, diferenta dintre Pb_a si 1/26 este variatia sa fata de distributia uniforma

Pentru o distributie uniforma, varianta este zero. Pb_i este probabilitatea ca doua caractere alese la intamplare din text sa coincida cu caracterul i. Insa probabilitatea de aparitie a unei litere nu este cunoscuta decat daca se cunoaste algoritmul prin care literele au fost generate. Aceasta probabilitate va fi aproximata pe baza frecventelor observate

Ambele metode (metoda Kasiski, cat si indexul de coincidenta) necesita disponibilitatea unei mari cantitati de text cifrat. Ele dau rezultate cand alfabetele de criptare sunt aplicate repetat la intervale periodice.

Substitutia "perfecta

Substitutia "perfecta- Substitutia ideala ar trebui sa foloseasca un numar mare de alfabete pentru o distributie de nerecunoscut si pentru a nu prezenta nici o forma aparenta, care sa permita alegerea unui alfabet la un moment dat.

Folosirea unui sir infinit nerepetitiv de alfabete contrazice metoda Kasiski

Astfel, o selectie nerepetitiva de alfabete de criptare va face imposibila criptanaliza cu metodele descrise mai sus.

Bloc notes-ul

Bloc notes-ul metoda de criptare in care un numar mare de chei nerepetitive se scriu pe cate o foaie de hartie, lipite impreuna intr-un bloc notes. Daca aceste chei au lungimea de 20 de caractere si trebuie trimis un mesaj de 300 de caractere, expeditorul va desprinde primele 15 foi din bloc notes, va scrie cheile una dupa alta deasupra mesajului in text clar si va cripta folosind o tabela asemanatoare cu tabloul Vigenere, dupa care va distruge cheile folosite.Exista doua probleme cu aceasta metoda: necesitatea unei sincronizari absolute intre expeditor si destinatar si nevoia unui numar nelimitat de chei.

Siruri de numere aleatoare mari

Siruri de numere aleatoare mari- o aproximare corecta a unui bloc notes utilizabil pe calculator este un generator de numere aleatoare. Aceste numere sunt de fapt, generate de calculator nu sunt aleatoare: in realitate ele formeaza un sir cu o perioada foarte mare care, in practica, este acceptabil pentru o perioada de timp limitata.

Expeditorul unui mesaj de 300 de caractere va genera pe calculator urmatoarele 300 de numere aleatoare, le va aduce in intervalul 0-25 si va folosi fiecare numar pentru a cripta caracterul corespunzator din mesajul in text clar. Daca sirul de numere aleatoare nu este suficient de lung, generatorul nu prezinta securitate.

Cifrul Vernam

Cifrul Vernam cifrul Vernam este un tip de bloc notes dezvoltat la AT&T, imun la majoritatea atacurilor criptanalitice. Criptarea de baza presupune un sir lung de numere aleatoare nerepetitive care sunt combinate cu mesajul in text clar

Cifrul Vernam binar

Cifrul Vernam binar-aceasta schema functioneaza si la criptarea unui mesaj binar, prin folosirea unui sir aleator de cifre binare care poate fi combinat modulo 2 cu bitii din mesaj. Rezultatul este un alt sir binar. Combinarea se poate face prin adunare modulo 2, ceea ce se realizeaza prin functia "sau exclusiv" sau "adunare fara transport". Aceste functii sunt implementate ca instructiuni masina, ceea ce simplifica aplicarea algoritmului.

Criptofrafia moderana

Criptografia a devenit stiintific ramura individualizata a matematicii, a fost in anul 1949 cand a fost publicat articolul 'Communication Theory of Secrecy Systems'. ,scris de Claude Shannon

Aceasta lucrare a pus bazele criptosistemelor simetrice

Criptografia moderna utilizeaza in principiu aceeasi algoritmi ca si criptografia traditionala (transpozitia si substitutia), dar accentul cade pe complexitatea algoritmilor. Obiectivul criptografic din actuala perioada este de a concepe algoritmi de criptare atat de complecsi si de ireversibili incat chiar si in situatia in care atacatorul (sau criptanalistul) avand la dispozitie cantitati mari de text criptat la alegerea sa, el sa nu poata face nimic fara cheia secreta

In criptografia moderna un sistem criptografic (criptosistem) este definit ca o structura cu cinci componente:

P = care este spatiul textelor in clar, scrise pentru un alfabet nevid T

K spatiul cheilor de criptare, kK

Familia functiilor de criptare dependenta de chei si de un algoritm de criptare E

Ek : P C , Ek =

Familia functiilor de decriptare dependenta de chei si un algoritm de decriptare D

Dk : C P , Dk =

C spatiul mesajelor cu text criptat unde:

C=

Cifrurile simetrice

Exista doua tipuri de sisteme simetrice (cunoscute si sub denumirea de sisteme cu cheie secreta): sisteme care se bazeaza pe algoritmi de tip bloc si sisteme care se bazeaza algoritmi de tip sir.

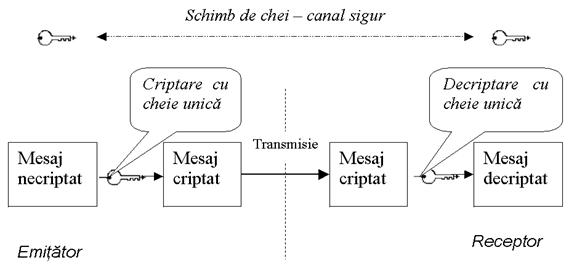
Fig.1.Schema de aplicare a unui algoritm simetric

Aceste sisteme de criptare folosesc aceeasi cheie K, atat la cifrarea cat si la descifrarea mesajelor. Cheia este tinuta secreta si este folosita in comun de catre emitator (cel care cifreaza mesajul M) si de catre receptor (cel care descifreaza criptograma C) Sistemele simetrice sunt bine cunoscute, conduc la performante bune si sunt folosite pentru protectia datelor utilizatorilor. Se pot aminti aici criptosisteme simetrice cunoscute, cum ar fi standardul american de cifrare DES (Data Encryption Standard) sau sistemul IDEA (International Data Encryption Algorithm). Securitatea criptarii simetrice depinde de protectia cheii; administrarea acestora este un factor vital in securitatea datelor si cuprinde urmatoarele aspecte: generarea cheilor, distributia cheilor si memorarea cheilor. Problema fundamentala este cea a gasirii unor modalitati de distributie sigura, periodica, a cheilor criptografice. In serviciile Internet se utilizeaza tot canalele retelei, folosind chei de cifrare a cheilor (numite si chei master). Sistemele simetrice, datorita cerintelor de distributie sigura a cheilor criptografice, sunt greoaie in utilizare in comunitatile mari de utilizatori din Internet.

Algoritmul DES

Algoritmul DES este o combinatie complexa folosind doua blocuri fundamentale in criptografie: substitutia si permutarea (transpozitia). Acest cifru bloc accepta un bloc de 64 de biti la intrare si genereaza un bloc cifrat de 64 de biti. DES este un algoritm simetric. Acelasi algoritm si aceeasi cheie sunt folositi atat la criptare cat si la decriptare

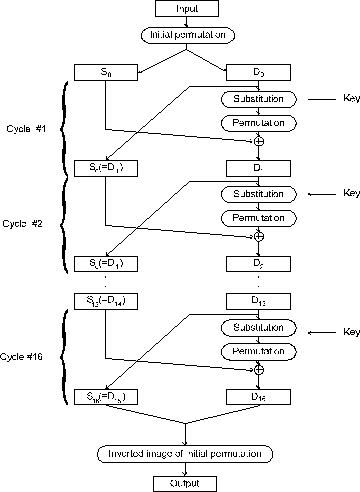
Fig 2.Detalii pentru folosirea algoritmului DES

La intrarea datele sunt impartite in blocuri de 64 biti, care sunt transformate folosind cheia de 64 de biti. Cei 64 de biti sunt permutati prin "permutarea initiala". In continuare, urmeaza operatiile ce constituie un ciclu. Blocul de 64 de biti este separat in doua, "jumatatea stanga" si "jumatatea dreapta", fiecare de 32 de biti. Cheia este deplasata la stanga cu un numar de biti si permutata: ea se combina cu "partea dreapta" care apoi se combina cu "partea stanga"; rezultatul devine noua "parte dreapta"; vechea "parte dreapta" devine noua "parte stanga

Pentru combinarea unei secvente de 32 biti cu cheia de 64 biti se folosesc expandari de la 32 biti la 48 biti si reducerea cheii de la 64 biti la 48 biti prin alegerea anumitor biti, operatii ce le numim "permutare expandata" si "permutare aleasa"

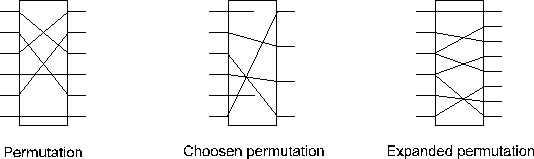
Fig.3.Manipularea permutarii in algoritmul DES

Algoritmul AES

In algoritmul AES rezultatul cifrat intermediar este numit vector state, care poate fi reprezentat ca un tabel cu patru linii si patru coloane, acestea fiind numerotate incepand de la 0.

Vectorul state se initializeaza cu blocul de 128 biti de text in clar (in ordinea coloanelor, cu primii patru octeti in coloana 0) si va fi modificat la fiecare pas al calculului, prin substitutii, permutari si alte transformari, rezultand in final blocul de 128 biti de text cifrat.

Cheia de 128 de biti este expandata in 11 tabele 4x4 notate rk(0), rk(1),., rk(10). Expandarea este realizata prin rotiri repetate si operatii XOR asupra unor grupuri de biti din cheia originala.

Calculul principal consta in executia a 10 runde, folosind cheia rk(i) la iteratia i. Fiecare runda consta in patru pasi.

Pasul 1 realizeaza o substitutie octet cu octet asupra vectorului state folosind o cutie S.

Pasul 2 roteste la stanga fiecare din cele 4 randuri ale vectorului state: randul 0 este rotit cu 0 octeti, randul 1 este rotit cu 1 octet, randul 2 este rotit cu 2 octeti si randul 3 este rotit cu 3 octeti, realizand difuzia datelor.

Pasul 3 amesteca fiecare coloana din vectorul state independent de celelalte, prin inmultirea coloanei cu o matrice constanta, multiplicarea fiind realizata folosind campul finit Galois GF(2⁸).

In fine, pasul 4 opereaza XOR cheia rk din runda respectiva cu vectorul state.

Algoritmul Lucifer

Algoritmul Lucifer-este o retea de permutari si substitutii, cu blocuri construite intr-o maniera asemanatoare cu DES. In DES, iesirea functiei f este operata XOR cu intrarea fazei anterioare pentru a forma intrarea fazei curente. In cazul lui Lucifer, "cutiile-S" au intrari si iesiri de 4 biti; intrarea este o permutare a bitilor iesirii din faza anterioara, iar intrarea din prima faza este chiar textul in clar. Un bit cheie este folosit pentru a alege intre "cutia-S" actuala din doua posibile - Lucifer implementeaza aceasta printr-o "cutie-T" cu 9 biti la intrare si 8 la iesire). Lucifer are 16 faze, blocuri de 128 de biti si o manipulare a cheii mai simpla decat DES-ul

Lucifer este mai sigur decat DES datorita lungimii mai mari a cheii si lipsei de rezultate publicate este nejustificat

Algoritmul Blowfish

Algoritmul Blowfish-Blowfish este optimizat pentru aplicatii in care cheia nu trebuie sa se schimbe des, cum ar fi legaturi de comunicatie sau un criptor automat pentru fisiere. Este semnificativ mai rapid decat DES cand este implementat pe procesoare de 32 de biti dotate cu memorie cache mare, cum ar fi Pentium. Blowfish nu este potrivit pentru comutarea de pachete, cu schimbari dese de cheie, ca functie hash one-way sau in aplicatii smart-card, unde memoria este insuficienta

Cifrurile asimetrice (cu chei publice)

Conceptul de criptografie cu chei publice a fost inventat de Whitfield Diffie si Martin Hellman. Contributia lor consta in propunerea de a folosi un nou criptosistem in care cheile de criptare si decriptare sunt diferite, iar cheia de decriptare (care este secreta) nu poate fi dedusa din cheia de criptare (care este publica). In anul 1976 conceptul a fost prezentat in premiera la Conferinta Nationala[4], iar citeva luni mai tarziu lucrarea a fost publicata

Un canal este o cale pentru fluxul de informatii; intr-un mediu privat, calea este protejata impotriva accesului din exterior. In general, un sistem cu n utilizatori necesita n*(n-1)/2 chei, pentru ca oricare pereche de utilizatori sa poata comunica intre ei si mesajele lor sa ramana secrete fata de ceilalti utilizatori. Numarul de chei creste rapid o data cu numarul de utilizatori; generarea, distribuirea si mentinerea securitatii cheilor constituie o problema datorita numarului lor mare

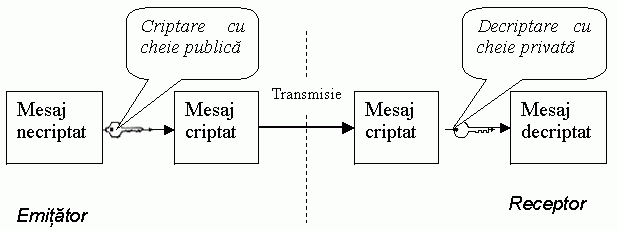
Fig.4.Schema de aplicare a unui algoritm asimetric

Intr-un sistem cu cheie publica, un utilizator detine doua chei: o cheie publica si o cheie privata. Utilizatorul isi poate face cunoscuta oricui cheia publica. Fie k_PRIV cheia privata si k_PUB cheia publica corespunzatoare. Atunci:

P=D(k_PRIV, E(k_PUB,P))

Utilizatorul poate decripta cu cheia privata ceea ce oricine altcineva a criptat cu cheia publica corespunzatoare.

Cu al doilea algoritm de criptare cu cheie publica

P=D(k_PUB, E(k_PRIV,P))

utilizatorul poate cripta un mesaj cu cheia privata, iar mesajul poate fi decriptat doar cu cheia publica corespunzatoare.

Aceste doua proprietati presupun ca cele doua chei, publica si privata, pot fi aplicate in orice ordine (sistemul RSA nu face distinctie intre cheia publica si cheia privata; orice cheie din perechea de chei poate fi folosita fie ca cheie publica, fie ca cheie privata).

Algoritmul Merkle-Hellman

Merkle si Hellman au dezvoltat un algoritm de criptare bazat pe problema rucsacului publicat in anul 1978 Problema rucsacului contine o multime de intregi pozitivi si o suma tinta si consta in gasirea unei submultimi de intregi a caror suma coincide cu suma tinta. Problema rucsacului este NP completa, adica rezolvarea sa necesita un timp exponential functie de marimea problemei - in acest caz, numarul de intregi.

Algoritmul incepe cu o multime de intregi in care fiecare element este mai mare decat suma predecesorilor sai. Sa presupunem ca avem un sir in care fiecare element a_k este mai mare decat a₁+a₂++a_k-1. Daca o suma este intre a_k si a_k+1, trebuie sa-l contina pe a_k, deoarece nici o combinatie de termeni a₁, a₂, , a_k-1 nu pot produce un total mai mare decat a_k. Analog, daca o suma este mai mica decat a_k, evident nu il va contine ca termen pe a_k

Problema rucsacului presupune un sir a₁, a₂, , a_n de intregi si o suma tinta T. Problema este de a gasi un vector de valori 0 si 1 astfel incat suma intregilor asociati cu 1 sa dea T.

Deci, dandu-se S=[a₁, a₂, , a_n], si T, sa se gaseasca un vector V cu valori 0 si 1 astfel incat :

Rezolvarea se face considerand fiecare intreg din S ca participand la T si reducand problema corespunzator. Cand o solutie nu produce suma tinta, se elimina intregul ales initial si se continua cu urmatorul. Acest back-traking deterioreaza viteza solutiei

Algoritmul IDEA

Un alt cifru renumit este IDEA (International Data Encryption Algorithm), realizat de doi cercetatori la Politehnica Federala din Zrich (ETHZ). Acest algoritm foloseste o cheie de 128 de biti si este inspirat din metodele anterioare - DES si cele imaginate pentru spargerea DES.

Algoritmul Rivest-Shamir-Adelman

Algoritmul Rivest-Shamir-Adelman (RSA)-incorporeaza rezultate din teoria numerelor, combinate cu dificultatea determinarii factorilor primi pentru un numar tinta. Ca in cazul algoritmului Merkle-Hellman si algoritmul RSA opereaza cu aritmetica modulo n. Un bloc in text clar este tratat ca un intreg, iar pentru criptare si decriptare se folosesc doua chei, e si d, care sunt interschimbabile. Blocul de text clar P este criptat ca Pe modulo n. Deoarece exponentierea este modulo n, este foarte dificil sa se factorizeze Pe pentru a descoperi textul original. Pentru aceasta, cheia de decriptare d este astfel aleasa incat (Pe)d = P modulo n. Astfel P este regasit fara a fi necesara descompunerea in factori primi a lui Pe. Cu algoritmul RSA, mesajul in text clar P este criptat in, mesajul in text cifrat C prin intermediul cheii de criptare e:

C = P^e modulo n

Mesajul in text clar este regasit cu ajutorul cheii de decriptare d:

P = C^d modulo n

Din cauza simetriei din aritmetica modulara, criptarea si decriptarea sunt mutual inverse si comutative:

P = C^d modulo n = (P^e)^d modulo n = (P^d)^e modulo n

Teoretic sunt trei posibilitati de abordare a unui atac in cazul algoritmului RSA: atacul in forta, atacul bazat pe metode matematice (incercarea factorizarii produsului a doua numere prime mari) si atacul temporal. Analiza acestor atacuri duce la concluzia ca nici unul nu are sorti de izbanda.

In pofida unor intense cercetari, au fost identificate doar probleme minore in comparatie cu cele din cazul algoritmului rucsacului a lui Merkle si Hellman

Problema autentificarii

Un alt domeniu in care a evoluat criptografia moderna este cel al crearii unor protocoale de autentificare - tehnica prin care un proces verifica daca partenerul de comunicatie este cel presupus si nu un impostor. Verificarea identitatii unui proces de la distanta este dificila si necesita utilizarea unor protocoale complexe, bazate pe tehnici criptografice

Problema poate fi imaginata intuitiv sub forma a doi parteneri care comunica si a altuia care doreste sa se introduca fraudulos in comunicatie, simuland pe oricare din partenerii de discutie. Ca o metoda de protectie, cei doi utilizatori pot stabili, de exemplu, o cheie secreta de sesiune, dar aceasta metoda presupune transmiterea cheii printr-un canal sigur; de aceea, se prefera, ca si in cazul impiedicarii interceptarilor, utilizarea criptarilor cu chei publice.

Unul din protocoalele de autentificare folosit in sistemele in timp real se numeste Kerberos (omonimul cainelui-paznic al lui Hades, care ii tinea pe cei nedoriti afara). Conectia securizata la un server aflat la distanta cu ssh foloseste pentru autentificare un alt protocol, bazat pe algoritmul cu cheie publica RSA.

Problema autentificarii impune gasirea unui corespondent electronic pentru semnaturile autorizate de pe documentele legale. Un asemenea corepondent se numeste semnatura digitala (vezi figura de mai jos) si presupune existenta unui sistem prin care una din parti sa poata transmite mesaje 'semnate' celeilalte parti, astfel incat:

1. receptorul sa poata verifica identitatea pe care pretinde ca o are emitatorul. Aceasta cerinta este necesara, de exemplu, in sistemele financiare: calculatorul trebuie sa se asigure ca un ordin de cumparare sau de plata apartine companiei cu al carei cont bancar se va opera.
2. transmitatorul sa nu poata renega ulterior continutul mesajului. Aceasta necesitate asigura protejarea bancilor impotriva fraudelor: un client necinstit ar putea acuza banca implicata in tranzactie, pretinzand, de exemplu, ca nu a emis un anumit ordin (de plata).
3. receptorul sa nu poata pregati el insusi mesajul. In cazul unei tranzactii financiare cu o banca, aceasta cerinta protejeaza clientul daca banca incearca sa-i falsifice mesajul.

Ca semnaturi digitale, se pot folosi semnaturi cu cheie secreta sau publica dar, asa cum s-a explicat anterior, de obicei se prefera cheile publice.

In cazul mesajelor transmise prin posta electronica, riscul legat de impersonificarea expeditorului este destul de mare fiindca standardele utilizate pentru transmiterea postei electronice sunt simple si in plus au fost facute publice (ceea ce inseamna ca oricine are acces la ele si poate sa le studieze). Standardul de e-mail (vezi 6) nu are la baza nici un sistem pentru verificarea identitatii celui care trimite un mesaj de posta electronica, bazandu-se pe o incredere reciproca intre utilizatori. Acest neajuns ar putea fi fructificat de catre persoane rauvoitoare pentru a trimite mesaje de posta electronica de pe adrese false, sau chiar de pe adrese existente, pretinzand ca sunt utilizatorii care detin acele adrese de posta electronica. Practic, este (aproape) imposibila identificarea unei persoane care a emis astfel de mesaje fiindca in Internet exista servere care asigura transmiterea anonima a mesajelor ('anonymous remailers'), trimitandu-le de la un server la altul de mai multe ori inainte de a le directiona catre adevarata destinatie.

Pentru autentificarea expeditorului unui mesaj (de posta electronica sau un ansamblu de date transmis prin Internet in alte scopuri) se foloseste cel mai adesea un sistem cu cheie publica. Astfel, daca expeditorul cripteaza mesajul cu cheia privata proprie, datele pot fi decriptate doar utilizand cheia publica pereche (vezi figura de mai jos), deci oricine poate verifica faptul ca mesajul a fost transmis intr-adevar de expeditor, si nu de o persoana ce pretinde a fi expeditorul (dupa cum s-a explicat deja, mesajul criptat cu o cheie poate fi decriptat doar utilizand cheia pereche acesteia si se presupune ca expeditorul este singurul care are acces la cheia sa privata).

Evident ca este posibil sa se realizeze o criptare a mesajelor in paralel cu autentificarea, astfel incat inclusiv datele transmise sa fie codificate. In acest caz, se vor utiliza perechile de chei privata, publica nu numai pentru autentificare, ci si pentru criptarea, respectiv decriptarea mesajelor transmise. Practic, pentru codificarea si semnarea digitala a unui mesaj emis, se va realiza o criptare cu cheia privata a emitatorului si apoi o criptare cu cheia publica a destinatarului. Astfel, destinatarul va putea decripta mesajul si autentifica provenienta sa in conditii de securitate.

Avand in vedere faptul ca algoritmii de criptare cu cheie publica consuma foarte mult timp, in general se implementeaza o tehnica putin diferita se utilizeaza o criptare cu cheie publica pentru transmiterea unei chei secrete generate aleator (deci cheia secreta este criptata si eventual se poate utiliza si autentificarea expeditorului), dupa care datele propriu-zise vor fi transmise criptate cu un algoritm simetric utilizand cheia secreta schimbata anterior. Aceasta metoda imbunatateste considerabil viteza de transmisie si de criptare / decriptare.

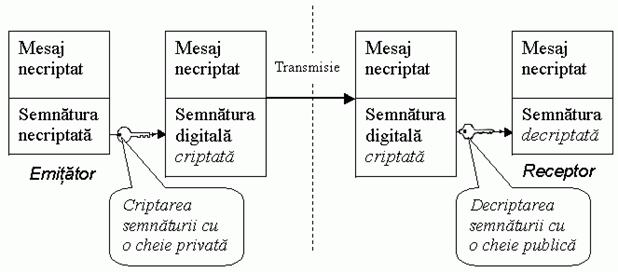
Fig.5.Semnarea digitala a mesajelor necriptate

Practic, pentru o identificare cat mai riguroasa a expeditorului se utilizeaza un sistem complex, bazat pe certificare, in care fiecare utilizator detine un certificat (ce are atasata o cheie publica si o cheie privata, secreta). Acesta este emis de o autoritate de certificare recunoscuta, in urma examinarii, pe baza de acte, a identitatii reale a persoanei. In momentul in care se doreste identificarea unei persoane, o cautare in baza de date a organizatiei respective va indica indentitatea expeditorului (pe baza cheii publice a acestuia, care este unica in lume).

Acest sistem este implementat sub forma unei structuri in care fiecare autoritate de certificare poate imputernici la randul ei alte organizatii sa emita certificate de autentificare, astfel incat originea unui certificat poate fi verificata in mod complet testand validitatea certificatului, apoi validitatea certificatului detinut de organizatia care a emis certificatului respectiv, si asa mai departe.

Sistemul de certificate digitale este utilizat nu numai pentru protejarea comunicatiilor, ci si pentru certificarea originii programelor. Astfel, prin folosirea unei criptari a programului de instalare cu cheia publica a firmei producatoare, utilizatorul poate verifica relativ usor ca acel program a fost creat intr-adevar de o anumita firma si pentru a decide daca sa instaleze sau nu programul. Aceasta este practic cea mai buna solutie de rezolvare a problemei rularii de programe / coduri daunatoare, enuntata la inceputul acestui capitol.

Problema modificarii mesajelor

Pentru a preveni modificarea unui mesaj, se utilizeaza o tehnica specifica, denumita tehnica hash, care permite construirea unui cod de identificare a datelor transmise, numit 'rezumatul datelor'. Principiile de baza ale tehnicii hash se aplica in numeroase domenii ale informaticii. Rezumatul unui mesaj se construieste prin aplicarea, in sens unic ('unisens'), a unei functii de transformare (functie 'hash') intr-o secventa de biti - de lungime mare, pentru a fi dificil 'spart'. Sensul unic de transformare asigura faptul ca nu se pot deduce datele de intrare pe baza datelor de iesire.

Datele ce trebuie transmise sunt utilizate ca si date de intrare, obtinandu-se astfel o valoarea de transformare ('hash value'). Daca datele in tranzit sunt modificate, la destinatie se va obtine o alta valoarea de transformare, ceea ce va indica falsificarea datelor.

Valoarea de transformare este in general criptata ulterior prin utilizarea aceleiasi chei secrete ca si pentru criptarea datelor transmise. Astfel, se formeaza o 'semnatura digitala' a datelor, care nu mai pot fi modificate fara ca acest lucru sa fie depistat.

Bibliografie

1.VV.Patriciu- Criptografia si securitatea retelelor de calculatoare cu aplicatii in C si Pascal,Ed.Tehnica,1994

2.T.Bajenescu- Progresele informaticii, criptografiei si telecomunicatiilor in secolul XX,Ed.Matrixrom

S.Iftene-Baze non-standard in criptografie.Tehnici de teoria numerelor

R..Oppliger-Contemporary Cryptography

A.Salomaa- Public-key cryptography

A. Menezes, P. Oorschot, S. Vanstome-Handbook of Applied Cryptography

www.wikipedia.org/

www.win.tue.nl