Metode generale deare a algoritmilor - Metoda Devide-and-Conquer (dezbina si stapineste)

Metode generale de proiectare a algoritmilor - Metoda Devide-and-Conquer (dezbina si stapineste)

Prin aceasta tehnica, o problema data P este impartita recursiv intr-un numar de subprobleme independente. Solutia unei probleme situate pe un anumit nivel al recursiei, se compune din solutiile subproblemelor sale. Daca penru fiecare nivel r al recursiei, subproblemele S_i(r), i=1,,q(r), ale acestui nivel satisfac conditia ca d(S_i(r)£k d(PT(S_i(r)) unde d(S_i) reprezinta dimensiunea subproblemei S_i, PT problema tata iar k este o constanta pozitiva subunitara, atunci adincimea recursiei este logaritmica. Relativ la arborele de calcul, "divide-and-conquer" realizeaza parcurgerea acestuia in stil " top-down" si apoi "bottom-up" .

Schema metodei pentru cazul arborelui binar de recursie:

d_and_c (P(n));

Avem:

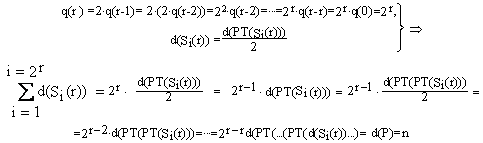
Deci pe oricare nivel al recursiei suma dimensiunea subproblemelor corespunzatoare acestui nivel este n.

Adecvata acestei metode este paradigma combinarii recursive.

Presupunind ca iesirile sint vectori de itemi de date (operanzi) de dimensiune n=2^d iar datele de intrare sint memorate initial intr-un vector A[0..n-1] care dupa executia algoritmului va contine rezultatele, paradigma poate fi descrisa astfel:

proc ALGORITM (l,l+n-1);

if (n>2)

Procedura ALGORITM este mult utilizata de o clasa larga de probleme, dintre care cele mai importante sint: sortarea, calculul permutarilor, convolutia, transformata Fourier.

Algoritmul Merge Sort (sortare prin interclasare)

Pentru a sorta o secventa de n elemente ale unui vector A, se imparte vectorul in 2 segmente de lungime n/2 care sint sortate separat recursiv, dupa care urmeaza interclasarea.

Pseudocod: Procedura MERGE_SORT primeste ca argumente A ‑ vectorul de sortat, si doi indici care delimiteaza o portiune din acest vector. Apelul initial va fi MERGE_SORT(A, 1, n).

MERGE_SORT(A, low, high)

Procedura MERGE interclaseaza secventele sortate A[lowmid] si A[mid+1high]. Pentru aceasta este nevoie de un vector auxiliar B, de aceeasi dimensiune cu A.

MERGE(A, low, mid, high)

Corectitudinea :

Lema 1: Procedura MERGE_SORT sorteaza crescator elementele vectorului A.

Demonstratie: Este suficient sa demonstram corectitudinea procedurii MERGE. Presupunem prin reducere la absurd ca in urma executiei procedurii MERGE exista un indice k pentru care B[k]>B[k+1]. Aceasta ar putea rezulta din urmatorele situatii:

1. B[k] fost initializat in bucla I iar B[k+1] in bucla II

2. B[k] a fost initializat in bucla I iar B[k+1] in bucla III

Cazul 1. Aceasta inseamna ca in imediat dupa initializarea elementului B[k] situatia indicilor i si j este urmatoarea : i mid si j > high. Deci A[i] >= A[high], B[k] = A[high] si B[k+1] = A[i]. Din B[k] > B[k+1] rezulta ca A[high] >A[i] >= A[high]. Absurd.

Cazul 2. Aceasta inseamna ca in imediat dupa initializarea elementului B[k] situatia indicilor i si j este urmatoarea : j high si i > mid. Deci A[mid] < A[j], B[k] = A[mid] si B[k+1] = A[j]. Din B[k] > B[k+1] rezulta ca A[mid] >A[j] > A[mid]. Absurd.

Complexitatea :

Lema 2.Timpul de executie al algoritmului MERGE_SORT este:

Demonstratie

Consideram: n = 2^k;

Evident procedura MERGE este de de complexitate O(n) .

T(n) = 2T(n/2) + n = 2 T(n/4) + n/2) + n = = 2²T(n/2²) + 2n= 2² (2T(n/2³) + n/2²) + 2n =
= 2³T(n/2³) + 3n = = 2^kT(n/2^k) + kn T(n) = kn = nlog₂n , pentru ca n = 2^k , si, deci, k=log₂n

Asadar complexitatea algoritmului este O(nlog n)

Algoritmul Quick_Sort (propus de C.A.R. Hoare)

Pentru a sorta o secventa de n elemente ale unui vector A, se partitioneaza vectorul in 2 segmente dupa schema urmatoare utilizind un element cu statut special numit pivot.

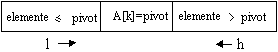
Urmeaza apoi sortarea recursiva a secventelor separate de pivot.

Quik_Sort(A, low, high)

Pseudocodul pentru functia partition:

Partition(A, low, high)

Procedura Partition considera pivotul ca fiind: A[low]. Indicele l parcurge vectorul de la stanga la dreapta, iar indicele h parcurge vectorul de la dreapta la stanga. Ei se apropie pana se intalnesc (l = h). Deci, l lasa in urma numai elemente A[i] pivot, iar h lasa in urma numai elemente A[i] pivot.

Ciclul I while inseamna ca inainteaza l cat timp A[l] pivot. Acest ciclu se opreste pe conditia A[l] pivot, fixandu-se aici.

Ciclul II while insemna ca inainteaza h cat timp A[h] pivot. Acest ciclu se opreste pe conditia A[h] pivot, fixandu-se aici.

Cele doua pozitii se schimba, astfel incat sa se permita inaintarea indicilor mai departe.

Corectitudinea:

Lema 1: Procedura Quick_Sort sorteaza crescator elementele vectorului A.

Demonstratie: Inductie dupa n.

Pasul 1. Pentru un tablou unidimensional A de dimensiune 2 evident algoritmul functioneza corect.

Pasul 2. Presupenem ca procedura Quick_Sort functioenaza coerct pentru tablori unidimensionale A de dimensiuni n si demostram ca functioneaza corect si pentru A de dimensiune n+1:

Prodedura Partition separa vectorul A in doua segmente S₁ cu elemente pivot si S₂ cu elemente > pivot.

Procedura Quick_Sort aplicata asupra vectorilor S₁ si S₂ functioneza conform ipotezei de inductie.

Rezulta in final A = S₁ È È S₂ . Datorita proprietatilor pivotului si a vectorilor S₁ si S₂ vectorul rezultat A este sortat crescator.

Complexitatea:

Lema 4. Timpul de executie al algoritmului Quick_Sort este:

Demonstratie

Cercetam cazul cel mai defavorabil. Fie cazul in care vectorul este ordonat descrescator. Pivotul gasit, la primul pas, este elementul maxim din vector, rezulta ca trebuie plasat in ultima pozitie. Pivotul va fi maximul dintre elementele secventei, deci, va fi plasat in ultima pozitie din secventa.

Problema se imparte in 2 subprobleme: P(n) P(n-1) , P(0).

Numarul de comparatii pentru functia Partition este (n-1). Vectorul se parcurge in doua directii, dar o singura data.

Rezulta ca timpul de functionare al algoritmului Quick_Sort este:

Rezolvand aceasta ecuatie, avem:

unde: T(1) este 0 (nu se partitioneaza). Rezulta:

Aceasta suma este de complexitate O(n²). Rezulta ca este un algoritm ineficient.

Spatiul ocupat de algoritmul Quick-Sort

Quick_Sort(A, low, high)

Avem in acest algoritm doua apeluri recursive.

Cazul cel mai defavorabil:

Consideram consumul de memorie in stiva : M(n) = c + M (n - 1) M(n) = O(n) un ordin de complexitate mare.

Pentru reducerea consumului de memorie, se concepe un alt algoritm la Quick_Sort, astfel incat un apel sa fie rezolvat recursiv, iar celalalt apel iterativ.

Quick_Sort(A, low, high)

Necesarul de memorie pentru aceasta este M(n) c + M(n/2), insemnand ca oricare ar fi secventa mai mica, ea este decat jumatatea secventei din care a fost obtinuta M(n) = O(log n) am redus ordinul de complexitate.