NoTiuni despre algoritmi Si programare structurata

Notiuni introductive

Rezolvarea problemelor cu ajutorul calculatorului presupune parcurgerea mai multor etape:

analiza problemei (cu stabilirea datelor de intrare/iesire) si modelarea ei matematica;

descrierea algoritmului cu ajutorul schemei logice si (sau) a pseudocodului;

scrierea programului intr-un limbaj de programare evoluat;

compilarea programului;

asamblarea programului;

executia programului.

Etapele 1.-3. sunt etape realizate de programator, iar etapele 4.-6. sunt realizate de catre sistemul de operare al calculatorului.

Un algoritm reprezinta o succesiune de calcule care, plecand de la conditii initiale cunoscute si cu ajutorul unor operatii efectuate mecanic fara aportul creator al omului, permite obtinerea solutiilor unor probleme dintr-o anumita clasa.

Altfel spus, un algoritm este un sistem de reguli care utilizand un set de date initiale ale unei probleme, dupa executia unui numar finit de pasi, faciliteaza obtinerea datelor finale, trecand printr-un sir de rezultate intermediare.

Un algoritm nu este aplicabil oricaror date initiale; o data initiala pentru care se poate aplica un algoritm se numeste data sau informatie admisibila.

Un algoritm trebuie sa satisfaca in general urmatoarele cerinte:

a)    claritate - descrierea algoritmului trebuie sa se faca precis, fara nimic arbitrar, fara ambiguitati si sa fie prevazute toate etapele de calcul si toate situatiile care se pot ivi pana la obtinerea solutiei;

b)   generalitate - algoritmul trebuie sa permita rezolvarea de probleme dintr-o intreaga clasa;

c)    finititudine - algoritmul trebuie sa furnizeze rezultatele intr-un numar finit (cat mai mic) de pasi;

d)   unicitate - etapele algoritmului trebuie sa fie definite in mod unic.

Operatiile de baza care apar intr-un algoritm sunt urmatoarele:

operatii de intrare iesire - datele de intrare se citesc, iar datele de iesire se afiseaza (se tiparesc);

operatii de atribuire - unei variabile i se atribuie valoarea unei expresii;

operatii de decizie - se determina valoarea de adevar a unei expresii logice si, functie de rezultatul obtinut, se ramifica rezultatul algoritmului.

Odata cu dezvoltarea informaticii a aparut si notiunea de programare structurata. La baza acestui concept sta ideea intocmirii algoritmilor folosind cateva structuri elementare, avand o singura intrare si o singura iesire.

In cazul programarii structurate, problema de rezolvat se descompune in subprobleme, a caror rezolvare duce la rezolvarea problemei initiale. Algoritmul, in acest caz, apare ca o secventa liniara de structuri elementare.

Structurile elementare sunt urmatoarele:

structura liniara - consta in executia neconditionata a unei secvente de instructiuni, un algoritm liniar fiind un algoritm in care etapele de calcul se succed una dupa cealalta;

structura alternativa - consta in ramificarea executiei algoritmului in functie de valoarea de adevar a unei conditii evaluate, algoritmii ramificati presupunand luarea unei anumite decizii in functie de care se continua executia pe ramuri distincte;

structura repetitiva - consta in executia repetata, de un numar finit de ori, a unei secvente de instructiuni. Un algoritm repetitiv presupune repetarea unor etape de calcul de un anumit numar de ori. Ansamblul etapelor ce se repeta alcatuiesc un ciclu. Daca numarul de repetari este cunoscut, ciclul se numeste cu numar cunoscut de pasi, iar daca nu este cunoscut, ciclul se numeste cu conditie sau cu numar necunoscut de pasi.

Subproblemelor obtinute prin descompunerea unei probleme le corespunde conceptul de subprogram.

Subprogramele pot fi tip functie sau tip procedura. Diferenta dintre functie si procedura consta in faptul ca functia transmite programului apelant o singura valoare, in timp ce procedura poate sa nu transmita programului apelant nici o valoare, sau sa transmita una sau mau multe valori.

Referirea unui subprogram poarta denumirea de apel.

O notiune de baza in programare o constituie notiunea de variabila. O variabila este caracterizata de patru elemente: nume, tip, valoare si adresa in memorie.

Numele unei variabile este format din unul sau mai multe caractere (litere si cifre, primul fiind litera), de exemplu: A, o ,min, X3.

Tipul indica multimea de valori posibile: intreg, real, sir de caractere, boolean etc.

Un tip variabila poate fi elementar sau structurat.

Tipurile structurate se obtin prin gruparea tipurilor elementare. Dintre acestea amintim tabloul, in care variabilele au acelasi nume si tip, deosebindu-se prin indici. Un tablou cu o singura dimensiune se numeste sir, iar un tablou cu doua dimensiuni se numeste matrice.

Adresa variabilei este adresa fizica din memoria calculatorului la care se afla valoarea variabilei. De obicei adresa este invizibila pentru programator.

Valoarea variabilei reprezinta valoarea efectiva pe care aceasta o are la un moment dat. Valoarea unei variabile se poate modifica numai printr-o instructiune de citire sau atribuire.

Reprezentarea algoritmilor

Pentru reprezentarea algoritmilor se pot utiliza mai multe metode:

schema logica;

pseudocodul (sau limbajul algoritmic);

limbajul de programare.

Primele doua sunt independente de tehnica de calcul, nu respecta o sintaxa rigida si sunt utile programatorului doar in faza de proiectare a algoritmilor.

Algoritmul scris intr-un limbaj de programare este singura forma direct utilizabila pe calculator, fiind un text codificat, pe baza unor legi sintactice bine determinate.

Schema logica

Schema logica este o reprezentare grafica ce permite vizualizarea inlantuirii si subordonarii secventelor de operatii. Schema logica foloseste simboluri grafice numite blocuri, care prin forma lor indica tipul operatiei, iar prin textul continut specifica semantica acesteia. Blocurile de baza sunt:

blocul delimitator sau terminal (fig. 1.a) - defineste inceputul (fig. 1.b) sau sfarsitul (fig. 1.c) unui algoritm, proceduri sau functii;

a) b) c)

Fig. 1. Blocuri delimitatoare.

blocul de citire/scriere (vezi fig. a) - se mai numeste si bloc de intrare/iesire si este utilizat pentru descrierea operatiilor de citire, respectiv, scriere. De exemplu, in fig. b, se citesc valorile variabilelor a si b , iar in fig. c, se scriu valorile variabilelor a si b;

a) b) c)

Fig. Blocuri de citire/scriere.

blocul de calcul - este utilizat pentru reprezentarea operatiei de atribuire (fig. 3.a). Efectul acestei operatii consta in evaluarea expresiei e si atribuirea rezultatului obtinut variabilei v.

De exemplu, in cazul operatiei din fig. 3.b, se aduna valorile variabilei a cu valoarea variabilei b si rezultatul se atribuie variabilei x. Efectul operatiei din fig.3.c consta in cresterea cu o unitate a valorii variabilei i;

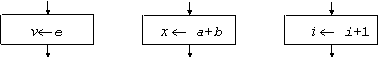
a) b) c)

Fig. 3. Blocuri de calcul.

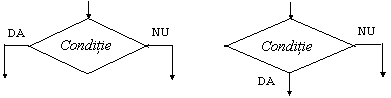
blocul de decizie (fig. 4.a si fig. 4.b) - are o intrare si doua iesiri, cate una pentru fiecare valoare de adevar. Daca in urma evaluarii conditiei rezultatul este "fals", se urmeaza calea "NU". In caz contrar, se urmeaza calea "DA".

a) b)

Fig. 4. Blocuri de decizie.

sagetile (fig. 5.a) - pun in evidenta inlantuirea logica a elementelor schemei logice;

blocul conector (fig. 5.b) - reprezinta punctele de urmarire si revenire ale schemei;

blocul de continuare (fig. 5.c) - reprezinta continuarea schemei logice la o alta pagina;

a) b) c)

Fig. 5. Sageata, blocurile conector si continuare.

blocul de procedura (fig. 6) - reprezinta apelul unei proceduri P. Procedura este o secventa de instructiuni descrisa printr-o schema logica separata si care are inscris in blocul terminal de inceput numele procedurii si eventualii parametrii.

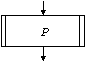
Fig. 6. Blocul de procedura.

Structuri elementare

In schemele logice pot sa apara urmatoarele structuri elementare:

a) structura liniara sau secventa (fig. 3.7.a) - este o insiruire de una sau mai multe actiuni (A, B, .) ce se executa secvential.

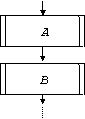
Fig. 7. Structura liniara.

Actiunile (A, B, .) pot fi blocuri: de calcul, de intrare-iesire, de procedura, sau combinatii liniare ale acestora. Structura liniara se executa neconditionat.

b) structura alternativa sau decizia (fig. 8.) - utilizeaza un bloc de decizie. Atunci cand este indeplinita conditia, executia programului se continua pe ramura "DA", adica se executa instructiunile din secventa A. In caz contrar, se executa instructiunile din secventa B.

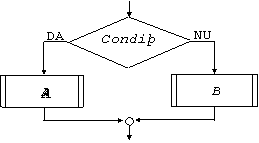
Fig. 8. Structura alternativa.

Structura alternativa poate sa apara si in una din variantele din fig.3.9.a sau fig.3.9.b

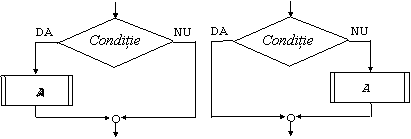
a) b)

Fig. 9. Variante de structuri alternative.

c) structura repetitiva sau ciclul - se bazeaza pe executarea repetata a unei secvente de blocuri. Aceasta structura trebuie sa contina o conditie care, la un moment dat, sa determine iesirea din structura repetitiva.

Exista trei tipuri de cicluri: while, repeat si for.

ciclul while (fig. 3.10.a) este caracterizat prin faptul ca secventa de instructiuni A se repeta atata timp cat conditia c este indeplinita. Se spune ca este un ciclu cu test initial deoarece, mai intai, se verifica daca este indeplinita conditia din blocul de decizie, dupa care se executa secventa de instructiuni A;

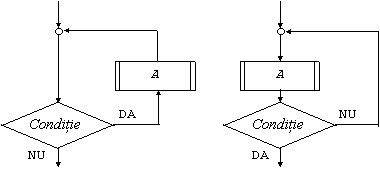ciclul repeat (fig. 3.10.b) este caracterizat prin faptul ca secventa de instructiuni A se repeta atata timp cat conditia c nu este indeplinita. Acesta este un ciclu cu test final deoarece, mai intai, se executa secventa de instructiuni A, dupa care se verifica daca este indeplinita conditia din blocul de decizie;

a) b)

Fig. 10. Structuri repetitive: a) de tip while; b) de tip repeat.

ciclul for (fig. 3.11) este caracterizat prin faptul ca secventa de instructiuni A se executa pentru fiecare valoare pe care o poate lua o variabila, numita contor. Contorul pleaca de la o valoare initiala si creste cu o anumita valoare, pana la o valoare finala. Iesirea din ciclu are loc atunci cand valoarea contorului devine mai mare decat valoarea variabilei finale.

In cazul ciclului din fig. 3.11, contorul, valoarea initiala a contorului, crestera contorului si valoarea finala a acestuia s-au notat cu i, v_i r si, respectiv, v_f. In cazul exemplului, iesirea din ciclu are loc atunci cand i > v_f.

Ciclurile de tip while si de tip repeat sunt cicluri cu un numar necunoscut de pasi deoarece, de cele mai multe ori, nu se cunoaste dupa cate executii ale secventei A are loc iesirea din ciclu.

Ciclul de tip for este un ciclu cu un numar determinat de pasi, deoarece se poate calcula de cate ori se executa secventa A.

In cazul ciclului while, secventa A poate sa nu fie executata niciodata, daca initial conditia ciclului nu este indeplinita.

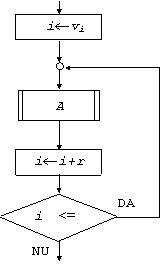
Fig. 11. Structura repetitiva de tip for.

In cazul ciclurilor repeat si for, secventa A este executata cel putin o data, chiar daca initial conditia ciclului nu este indeplinita.

1. Exemple de scheme logice

Pentru exemplificare, se vor intocmi schemele logice pentru rezolvarea ecuatiei de gradul doi cu coeficienti reali si pentru calculul sumei a n numere reale.

1.1. Ecuatia de gradul doi

Se da ecuatia de gradul doi: ax² + bx + c = 0, unde a, b, cIR

Se cere sa se intocmeasca algoritmul ce furnizeaza solutiile reale ale acestei ecuatii.

Situatiile ce apar la rezolvarea ecuatiei sunt urmatoarele:

daca a = 0, ecuatia degenereaza intr-o ecuatie de gradul unu, situatie semnalizata printr-un mesaj;

daca a 0, se calculeaza delta = b²- 4ac;

daca delta < 0, printr-un mesaj se semnalizeaza faptul ca ecuatia are radacini complexe;

daca delta >= 0, se calculeaza radacinile x₁, x₂ si se afiseaza.

Avand in vedere aceste situatii, rezulta schema logica din fig. 1

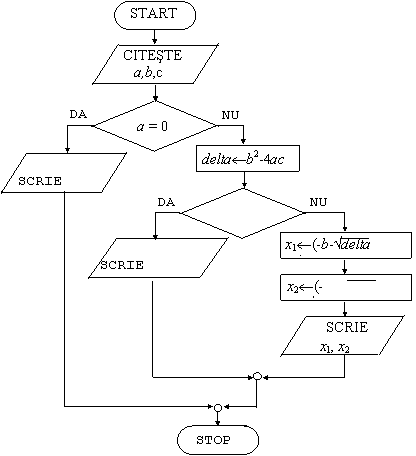
Fig. 1 Schema logica pentru rezolvarea ecuatiei de gradul doi.

1. Suma a n numere reale

Fiind date n numere reale: a₁, a₂,., a_n, se cere sa se intocmeasca schema logica ce calculeaza suma celor n numere.

La calculul sumei, se evidentiaza urmatoarele etape de calcul:

se citeste n;

se citesc cele n numere reale, cu ajutorul unui ciclu for ;

se initializeaza suma (notata cu s) cu valoarea zero;

se calculeaza suma celor n numere reale, tot cu ajutorul unui ciclu for ;

se afiseaza suma.

Se obtine schema logica din fig. 13.

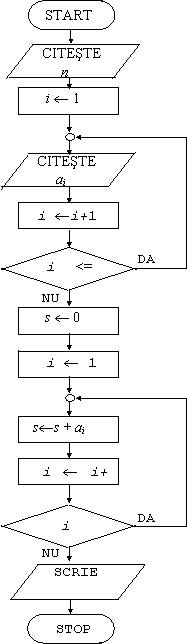
Fig. 13. Schema logica pentru calculul sumei a n numere reale.

O schema logica prezinta urmatoarele dezavantaje:

schema logica nu este liniara;

in schema logica nu se pot insera declaratii si comentarii;

citirea unei scheme logice este greoaie.

O schema logica prezinta urmatoarele dezavantaje:

schema logica nu este liniara;

in schema logica nu se pot insera declaratii si comentarii;

citirea unei scheme logice este greoaie.

3. Pseudocodul

Pseudocodul permite o descriere mai liniara a algoritmului, usurand atat reprezentarea cat si citirea acestuia. Pseudocodul se apropie mult de limbajul de programare PASCAL, cu toate ca nu are o sintaxa rigida ca aceea a unui limbaj de programare.

Instructiunile pseudocodului sunt urmatoarele:

1. algoritmul nume este :

Aceasta instructiune este prima din program si are rolul de a denumi programul. Instructiunea corespunde blocului START din schema logica (vezi fig 3.1.b).

De exemplu: algoritmul valoare_polinom este :

citeste lista variabile

Efectul acestei instructiuni consta in citirea valorilor variabilelor din lista (prin lista variabile se intelege o succesiune de variabile separate prin virgula). Instructiunea corespunde blocului de citire din schema logica.

De exemplu, instructiunea corespunzatoare blocului de citire din fig 3.b este urmatoarea: citeste a,b;

3. scrie lista variabile

Efectul acestei instructiuni consta in afisarea valorilor variabilelor din lista. Ea corespunde blocului de scriere din schema logica.

De exemplu, instructiunea corespunzatoare blocului de scriere din fig 3.c este urmatoarea: scrie a,b;

variabila expresie;

In cazul acestei instructiuni, valoarea calculata a expresiei se atribuie variabilei specificate in membrul stang. Instructiunea corespunde blocului de calcul din schema logica (vezi fig 3.3.a).

De exemplu, instructiunea corespunzatoare blocului din fig 3.3.b este urmatoarea: x a + b;

5. daca conditie atunci secventa de instructiuni A

[altfel secventa de instructiuni B]

sfarsit_de_daca;

Aceasta instructiune corespunde structurii alternative din schema logica (vezi fig. 3.8).

Efectul acestei instructiuni consta in verificarea conditiei specificate si executia secventei de instructiuni A, atunci cand conditia este indeplinita, sau executia secventei de instructiuni B, atunci cand conditia nu este indeplinita.

Ramura asociata cuvantului cheie altfel este optionala (de aceea s-a pus intre paranteze patrate), adica, in anumite cazuri, aceasta poate lipsi. In asemenea situatii, instructiunea este urmatoarea:

daca conditie atunci secventa de instructiuni A

sfarsit_de_daca;

si corespunde structurii alternative din fig. 3.9.a;

6. caz conditie 1 : secventa instructiuni 1

conditie 2 : secventa instructiuni 2

.

conditie n : secventa instructiuni n

[altfel secventa de instructiuni n+1]

sfarsit_de_caz

Aceasta instructiune este o structura alternativa cu n+1 cai si poate fi echivalata cu mai multe structuri alternative, conectate in cascada.

Conditiile ce prefixeaza secventele de instructiuni trebuie sa fie disjuncte doua cate doua.

Ramura cu altfel poate sa lipseasca.

Executia acestei instructiuni consta in urmatoarele:

se verifica conditiile;

daca una din conditii este indeplinita, se executa secventa de instructiuni ce urmeaza conditiei indeplinite, altfel:

se executa secventa ce urmeaza dupa cuvantul altfel, daca aceasta ramura exista, sau, in caz contrar,

se trece la executia instructiunii ce urmeaza dupa sfarsit_de_caz.

Instructiunea caz nu are un bloc corespondent in schema logica. Totusi ea poat fi asimilata cu mai multe structuri alternative conectate in cascada. De exemplu, instructiunea:

caz conditie 1 : secventa instructiuni A

conditie 2 : secventa instructiuni B

altfel secventa instructiuni C

sfarsit_de_caz

este echivalenta cu structura de schema logica din fig. 3.14,

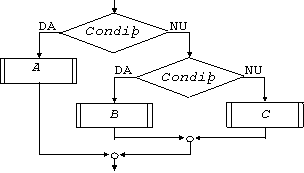
Fig. 3.14. Structura logica echivalenta cu o instructiune caz

cu doua cai si ramura altfel.

iar instructiunea:

caz conditie 1 : secventa instructiuni A

conditie 2 : secventa instructiuni B

sfarsit_de_caz

este echivalenta cu structura de schema logica din fig. 3.15.

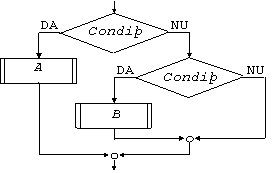
Fig. 3.15. Structura logica echivalenta cu o instructiune caz

cu doua cai si fara ramura altfel.

7. cat_timp conditie executa

secventa de instructiuni A

sfarsit_de_cat_timp

Aceasta instructiune corespunde structurii repetitive de tip while (vezi fig. 3.10.a).

Executia instructiunii consta in urmatoarele etape:

se verifica conditia;

se executa secventa de instructiuni A, atunci cand conditia este indeplinita, sau, in caz contrar, se trece la executia instructiunii ce urmeaza dupa sfarsit_cat_timp.

Daca, initial, conditia nu este indeplinita, secventa de instructiuni A nu se executa.

8. repeta

secventa de instructiuni A

pana_cand conditie

Aceasta instructiune corespunde structurii repetitive de tip repeat (vezi fig. 3.10.b).

Executia instructiunii consta in urmatoarele etape:

se executa secventa de instructiuni A;

se verifica conditia;

atunci cand conditia nu este indeplinita, se executa secventa de instructiuni A, sau, in caz contrar, se trece la executia instructiunii ce urmeaza dupa pana_cand.

Chiar daca initial conditia nu este indeplinita, secventa A se executa cel putin o data.

9. pentru i=v_i, v_f [, r] executa

secventa de instructiuni A

sfarsit_de_pentru;

Aceasta instructiune corespunde structurii repetitive de tip for (vezi fig. 3.11).

Executia instructiunii consta in urmatoarele etape:

se da variabilei (contorului) i valoarea initiala v_i;

se executa secventa de instructiuni A;

se creste valoarea variabilei i cu valoarea (pasul) r;

daca valoarea variabilei i este mai mica sau egala cu valoarea finala v_f, se executa secventa A, sau, in caz contrar, se trece la executia instructiunii ce urmeaza dupa sfarsit_de_pentru.

Specificarea valorii pasului r este optionala. In cazul in care valoarea lui r nu se specifica, se considera r =1.

10. stop;

Aceasta instructiune determina terminarea executiei programului, deci este ultima instructiune dintr-un program.

In schema bloc, acestei instructiuni ii corespunde blocul delimitator din fig. 3.1.c.

11. procedura nume [(lista parametri formali)];

secventa de instructiuni

sfarsit_procedura

Aceasta instructiune permite declararea procedurilor.

Declararea unei proceduri consta in declararea numelui procedurii si declararea listei parametrilor formali (lista care este optionala).

Parametrii formali sunt parametrii ale caror valori fie sunt preluate din programul apelant, fie sunt transmise programului apelant. Rezulta ca, la apelul procedurii, valorile acestor parametrii sunt actualizate.

In lista, parametri formali se separa prin virgula.

1 nume lista parametri actuali

Apelul unei proceduri se face specificand numele procedurii urmat de lista parametrilor actuali. In lista, parametri actuali se separa prin virgula.

13. ciclu

Cu aceasta instructiune se determina trecerea la sfarsitul celui mai interior ciclu ce contine aceasta instructiune (deci la un sfarsit_de_cat_timp, la un pana_cand, sau la un sfarsit_de_pentru), fara a se produce iesirea din ciclu.

14. iesire;

Acaesta instructiune determina trecerea la prima instructiune ce urmeaza celui mai interior ciclu ce contine aceasta instructiune. Practic, se provoaca iesirea fortata din ciclul respectiv;

Incadrate de acolade, comentariile pot sa apara oriunde in program.

La executia programului, rezultatul parcurgerii comentariilor este nul, acestea avand o valoare informativa numai pentru cel care citeste programul.

3.1. Exemple de algoritmi descrisi in pseudocod

Pentru exemplificare, se vor intocmi algoritmii de rezolvare a ecuatiei de gradul doi cu coeficienti reali si calculul sumei a n numere reale, dar in pseudocod.

3.1.1. Ecuatia de gradul doi

Utilizand pseudocodul, pentru aplicatia 3.1.1, rezulta:

algoritmul ecuatie_de_gradul_doi este:

citeste a, b, c;

daca a = 0 atunci scrie "Ecuatie de gradul I"

altfel delta b - 4ac;

daca delta< 0 atunci scrie "Radacini complexe"

altfel x₁ b delta )/(2a);

x₂ b delta )/(2a);

scrie x₁ x₂;

sfarsit_de_daca;

sfarsit_de_daca;

stop.

3.1. Suma a n numere reale

Cu ajutorul pseudocodului, algoritmul de calcul a sumei a n numere reale (vezi aplicatia 3.1.2) rezulta:

algoritmul suma_a_n_numere_reale este :

citeste n;

pentru i =1, n executa

citeste a_i

sfarsit_de_pentru;

s ;

pentru i =1, n executa

s s + a_i

sfarsit_de_pentru;

scrie s;

stop;