O implementare in timp liniar a SPQR-tree - Algoritmul - Gutwenger si Mutzel

O implementare in timp liniar a SPQR-tree - Algoritmul - Gutwenger si Mutzel

Rezumat. Structura de date SPQR-tree reprezinta descompunerea unui graf biconex in raport la componentele sale triconexe. SPQR-tree a fost introdus de Di Battista si Tarnassia, devenind un concept important in teoria grafurilor. Articolele teoretice privitoare la SPQR-trees sustin ca acestia poate fi implementati in timp liniar folosind o modificare a algoritmului lui Hopcroft si Tarjan pentru descompunerea unui graf in componente triconexe.

Pana acum nu se cunoaste nici o implementarea corecta -liniara in timp-, a descompunerii triconectivitatii sau a SPQR-trees. In acesta articol, aratam incorectitudinea algorimului Hopcroft si Tarjan, si corectam partile gresite. Descriem relatia dintre SPQR-tree si componentele triconexe si aplicam algoritmul rezultat in determinarea SPQR-trees.

1. Introducere.

Structura de date SPQR-tree reprezinta descompunerea unui graf biconex in raport la componentele sale triconexe. SPQR-tree a fost introdus de Di Battista si Tarnassia, devenind un concept important in teoria grafurilor.

Incepand de atunci, SPQR-trees au devenit o structura de date importanta. Multi algoritmi liniari care functioneaza doar pentru grafuri triconexe pot fi extinsi pentru grafuri biconexe, folosind SPQR-trees.

In acest articol prezentam un algoritm liniar pentru implementarea structurii de date SPQR-trees. Descriem relatia dintre SPQR-tree si componentele triconexe si aratam incorectitudinile algoritmului lui Hopcroft si Tarjan. Vom realiza un algoritm corect pentru descompunerea grafurilor in componente triconexe prin corectarea si inlocuirea partilor gresite, aplicandu-l si in calcularea SPQR-trees. Articolul este structurat dupa cum urmeaza:

In sectiunea 3 sunt descrise notiunile de baza privitoare la SPQR-trees si componentele triconexe;

In sectiunea 4 este prezentat algoritmul pentru determinarea SPQR-trees si a descompunerii triconexe.

In sectiunea 5 se prezinta partile incorecte ale algoritmului Hopcroft /Tarjan si corectiile aduse.

2. Notiuni introductive

Fie graf G=(V,E) un multigraf neorientat , in care V reprezinta multimea de varfuri si multimea E a muchiilor, continand perechi neorientate (v,w)IV. O muchie (v,v) este numita "self-loop". Daca perechea (u,v) se regaseste in E de mai multe ori atunci ea se numeste muchie multipla. Graful G este simplu daca nu contine self-loop si muchii multiple.

Daca E' este o multime de muchii a lui G, V(E') este un set de noduri incidente in una sau mai multe muchii din E'.

Un drum p:vÞw in G este o secventa de varfuri si muchii care duce de la v la w. Drumul este elementar(simplu) daca toate varfurile sunt distincte. Daca p:vÞw este un drum simplu atunci p plus muchia (w,v) este ciclu.

Un multigraf neorientat este conex daca pentru orice pereche de varfuri exista un drum care le uneste. Un multigraf conex G este biconex, daca pentru orice triplet de varfuri distincte, v, w si q din V, exista un drum p:vÞw, astfel incat q nu este pe acest drum.

Fie G=(V,E) un multigraf biconex si a,b IV. Multimea E poate fi impartita in clase de echivalenta E₁, E₂..E_n astfel incat doua muchii sunt in aceeasi clasa, daca orice drum comun a lor, nu contine varfurile decat ca extremitati finale.

Clasele E_i se numesc clase de separatie a lui G in raport cu (a, b). Daca exista cel putin doua clase de separatie, atunci este o pereche separabila lui G, mai putin in situatia in care (i) exista exact doua clase de separare si una dintre ele este formata din exact o muchie, sau (ii) exista exact trei clase de echivalenta, fiecare fiind formata din exact o muchie. Daca G nu contine perechi de separatie, atunci ele este triconex.

Un arbore cu radacina T este un digraf, a carui versiune neorientata este conexa, avand un varf numit radacina care nu este extremitate finala pentru nici un arc si toate celelalte varfuri reprezinta extremitate finala pentru exact un arc. Relatia " (v,w) este un arc in T " este notata v w. Relatia "este un drum de la v la w in T " este notata vw. Daca v w atunci v est eparintele lui w, iar w este copilul lui v. Daca vw atunci v este ascendent pentru w iar w este descendent a lui v. Multimea descendentilor a varfului v este notata cu D(v). Fiecare varf este un ascendent si un descendent al sau. Daca G este un multigraf orientat, un arbore T este un arbore de acoperire a lui G, daca T este un subgraf a lui G care contine toate varfurile lui G.

Un palm tree P este un multigraf orientat astfel incat fiecare arc din P este fie arc din arbore, notat v w fie frond notat v w satisfacand urmatoarele proprietati:

i. Subarborele T format din toate arcele v w este un arbore de acoperire a lui P.

ii. Daca v w atunci wv.

Fie G=(V,E) un multigraf biconex, o pereche de separare a lui G si E₁,E₂,.E_n clasele de echivalenta a lui G in raport cu . Fie E' = E₁ÈE₂È ÈE_k. Si E" = E_k+1ÈE_k+2È ÈE_n. astfel incat |E'| ³ 2, |E'| ³ 2. Grafurile G₁=((V(E'), E'È ) si G₂ =(V(E'), E' È ) se numesc "split graph-uri" a lui G, in raport cu , unde e o noua muchie. Inlocuirea unui multigraf G cu doua "split graph-uri" se numeste "impartirea" lui G (splitting G). Fiecare split-graf este de asemenea biconex. Fiecare muchie e este numita muchie virtuala si identifica operatia split.

Presupunem ca G este impartit, apoi split-grafurile se impart si asa mai departe pana cand nu mai sunt posibile noi impartiri. Grafurile rezultate sunt numite componentele split ale lui G. Fiecare dintre ele sunt:

Un set de trei muchii multiple (triple bond)

Un ciclu de lungime trei

Un graf simplu triconex.

Componentele split nu sunt in mod necesar unice.

Lema 1. Fie G un multigraf:

i. Fie care muchie din E apare in exact o componenta split si fiecare muchie virtuala apare in exact doua componente split.

ii. Numarul total de muchii din componentele split sunt cel mult 3|E|-6.

Fie G₁=(V₁,E₁) si G₂=(V₂,E₂) sunt doua componente "split", amandoua continand o muchiie virtuala e. Atunci G'=(V₁ È V₂ , E₁ È E₂-) este numit "merge graph" a lui G₁ si G₂.

Inlocuirea a doua componente G₁ si G₂ prin "merge"-graful lui G' se numeste operatia "merge" a lui G₁ si G₂. Componentele triconexe ale lui G se obtin din componentele split prin unirea legaturilor triple (triple bonds) intr-o multime maximala de muchii multiple (bonds) si a triunghiurilor in cicluri simple maximale(poligonuri)

Lema 2. Componentele triconexe ale lui G sunt unice.

Componentele triconexe sunt strans legate de SPQR-trees. SPQR-trees au fost initial definite doar pentru grafurile planare.

Fie G un graf biconex. O pereche split a lui G este fie o pereche de varfuri adiacente fie o pereche de separatie. O componenta split a unei perechi split este fie o muchie (u,v), fie un subgraf maximal C al lui G in care nu este o pereche split a lui C. Fie o pereche split a lui G. O pereche a lui G este pereche split maximala in raport cu daca pentru orice pereche split , varfurile u , v, s, t sunt in aceeasi componenta split.

Fie e = (s, t) o muchie a lui G, numita muchia de referinta. Arborele SPQR T al lui G raportat la e este un arbore cu radacina ale carui noduri sunt de patru tipuri: S, P, Q si R. Fiecare nod μ al lui T are asociat un multi-graf biconex numit scheletul lui μ. Arborele T este definit recursiv dupa cum urmeaza:

Cazul trivial: Daca G se compune din exact doua muchii paralele intre s si t , atunci T se compune dintr-un singur nod Q al carui schelet este chiar G.

Cazul paralel: Daca perechea de separare are cel putin trei componente split G₁, . , G_k, radacina lui T este un nod de tip P din μ, al carui schelet se compune din k muchii paralele e=e₁,.,e_k intre s si t.

Cazul serie : Altfel, perechea de separatie are exact doua componente split, una din ele este e, iar cealalta este data de G". Daca G" are puncte de articulatie c₁, . , c_k-1 ( k≥2 ) care impart graful in componentele G₁ . G_k, in aceasta ordine de la s la t, radacina lui T este un nod de tip S μ, al carui schelet este ciclul e₁, . , e_k, unde e₀ = e, c₀ = s, c_k = t, iar e_i = ( c_i-1, c_i ) ( i = 1, . , k ).

Cazul rigid : Daca niciunul din cazurile de mai sus nu se aplica, fie ,., perechile impartite maximale in raport cu (k≥1), si, pentru i = 1,., k, fie G_i reuniunea tuturor elementelor impartite ale in afara celei car il contine pe e. Radacina lui T este un nod de tip R, al carui schelet se obtine din G inlocuind fiecare subgraf G_i cu muchia e_i = (s_i, t_i ).

Cu exceptia cazului trivial, μ are fii pe μ₁ . μ_k astfel incat μ_i este radacina arborelui SPQR al lui G_i U e_i in raport cu e_i ( i = 1,.,k ). Extremitatile muchiei e_i sunt numite poli ai nodului μ_i. Muchia virtuala a nodului μ_i este muchia e_i a scheletului lui μ. Arborele T este completat adaugand un nod de tip Q, reprezentand nodul-referinta e, si marcandu-l ca parinte al lui μ, devenind astfel radacina.

Fiecare muchie in G este asociata cu un nod de tip Q din T. fiecare mushie e_i din scheletul μ este asociata cu fiul μ_i al lui μ. Este posibil sa notam ca radacina a lui T un nod arbitrar μ' de tip Q, rezultnd un arbore SPQR raportat la muchia asociata lui μ'. In implementarea noastra folosim o definitie putin diferita, dar echivalenta, a arborelui SPQR. Omitem nodurile de tip Q si facem in schimb diferenta intre muchii reale si muchii virtuale in graful schelet. O muchie in scheletul lui μ care este asociata cu un nod de tip Q din definitia originala este o muchie reala care nu este asoiata vreunui fiu al lui μ, toate celelalte muchii de schelet sunt asociate cu noduri de tip P, S sau R. Folosind definitia modificata, putem demonstra ca grafurile schelet sunt componentele unice triconexe ale lui G:

Teorema 1. Fie G un multi-graf biconex si T arborele sau SPQR.

(i)          Grafurile schelet ale lui T sunt componentele triconexe ale lui G. Nodurile de tip P corespund legaturilor, nodurile de tip S corespund poligoanelor, iar nodurile de tip R sunt grafuri simple triconexe.

(ii)        Exista o muchie intre doua noduri μ, v apartin lui T daca si numai daca elementele triconexe corespunzatoare au in comun o muchie virtuala.

(iii)       Dimensiunea lui T, inclusiv a tuturor grafurilor-scheleti este liniara raportat la dimensiunea lui G.

Demonstratie ( succinta ) Observam ca daca este o pereche de separatie, componentele impartite ale lui sunt clase de separare in raport cu . In cazurile paralel, serie si rigid ale definitiei arborelui SPQR, subgrafurile G₁,.,G_k sunt luate in considerare. Presupunem ca G₁,.,G_l contin mai mult de o muchie si G_l+1,.,G_k contin exact o muchie. In fiecare din cele trei cazuri, pasul de dezcompunere recursiva poate fi realizat prin efectuarea a l operatii de impartire, fiecare desprinzand un G_i, 1≤i≤l si introducand o noua muchie virtuala e' in scheletul nodului μ si in scheletul unui fiu μ_i al lui μ. Devreme ce e' ramane in scheletul lui μ_i in pasi consecutivi, urmeaza partea (ii) a teoremei.

Grafurile-scheleti finale sunt fiecare un poligon, o legatura sau un drum simplu triconex si oricare doua poligoane, ca si oricare doua legaturi nu au in comun nicio muchie virtuala. Prin urmare, grafurile-scheleti sunt descompunerea unica in elemente triconexe a lui G demonstrand partea (i). Ultima partea a teoremei reiese direct din (i) si Lema 1.

4. Algoritmul

Fie G un multi-graf triconex fara cicluri. Conform Teoremei 1, este suficient sa calculam componentele triconexe ale lui G, acestea dandu-ne suficiente informatii pentru a construi arborele SPQR al lui G. Corectam partile defectuoase din algoritmul lui Hopcroft si Tarjan si aplicam acest algoritm pentru gasirea componentelor triconexe. Ne concentram asupra gasirii perechilor de separatie deoarece desrierea acestei parti in [15] nu este doar confuza dar contine si erori grave. Pentru o imagine de ansamblu asupra algoritmului lui Hopcroft si Tarjan, consultati [13] sau [15].

4.1 Identificarea arborilor SPQR

Datele de intrare ale algoritmului reprezinta un multi-graf biconex G = (V , E) si o muchie de referinta e_r. La primul pas, Muchiile multiple sunt inlocuite cu o muchie virtuala, dupa cum arata in Algoritmul [1]. Aceasta creaza un set de legaturi C₁,.,C_k, rezultand un graf simplu G'. Sortarea necesara a muchiilor din linia 1 poate fi facuta in O(|V| + |E|) folosind bucket sort de doua ori. Prima data se sorteaza dupa varful cu index mai mic, apoi dupa cel cu index mai mare, presupunand ca varfurile au indici distincti in intervalul 1,..,|V|. Bucla for din linia a 2-a parcurge toate muchiile deci Algoritmul 1 are complexitatea O(|V| + |E|).

Algoritmul 1: Impartirea muchiilor multiple

1.1 Sortarea muchiilor astfel incat toate muchiile multiple sa vina una dupa cealalta.

1.2 pentru fiecare grup maximal de muchii multiple e₁,.,e_l cu l ≥ 2 executa

fie e₁,.,e_l muchii intre v si w

inlocuieste e₁,.,e_l cu o noua muchie e' = ( v , w )

creaza o noua componenta C =

sfarsit_pentru

Al doilea pas determina componentele split C_k+1,..C_m a lui G'. Rutina este prezentata in detaliu in subsectiunea urmatoare. Componentele triconexe ale grafului initial G, sunt create prin reansamblarea partiala a componentelor C₁,.C_m. Cat timp duua legaturi(bonds) sau doia poligoane C_i si C_j contin aceeasi muchie virtuala, ele sunt unite. Aceasta este prezentata in algoritmul 2. Componentele sterse sunt marcate ca vide. Bucla forall din linia 2.1 treverseaza toate muchiile din C_i care au fost adaugate la C_i in timpul iteratiilor. Testul din linia 2.1 poate fi facut in timp constant preprocesand pentru fiecare muchie virtuala e cele doua componente care-l contin pe e. Reprezentam muchiile dintr-o componenta C_i printr-o lista de muchii care permit implementarea setului de operatii din liniile 2.3 si 2.4. in timp constant. In acord cu Lema 1, numarul total de muchii din toate componentele este O(|E|), deci algoritmul 2 poate fi implementat in O(|V| + |E|).

Algoritmul 2: Construirea componentelor triconexe

pentru i 1 , m executa

daca C_i ¹ Æ and C_i este "bond" sau "poligon" atunci

2.1 pentru_toate e I C_i executa

2.2 daca exista j ¹ i cu e I C_j si type(C_i)=type(C_j) atunci

2.3 C_i (C_i È C_j)

2.4 C_j Æ

Sfarsit_daca

Sfarsit_pentru

Sfarsit_daca

Sfarsit_pentru

Pasul precedent ne da destule informatii pentru a contrui SPQR-tree T a lui G. Aplicand teorema 1 este simplu de construit versiunea fara radacina (unrooted) a lui T. Deoarece omitem nodurile de tip Q din reprezentare, vom "root" T din nodul al carui schelete contine muchia referinta e_r. In timpul constructiei vom crea cross-links intre fiecare muchie a arborelui μ v din T si cele doua muchii virtuale corespunzatoare din scheletul lui μ si scheletul lui v.

4.2. Indentificarea perechilor de separatie

Presupunem ca am obtinut un palm tree P pentru un graf simplu biconex G'=(V,E'), iar varfurile din G' sunt numerotate 1, .|V|. In cele ce urmeaza vom identifica varfurile cu numere. Introducem notatia urmatoare:

lowpt1 = min (È

lowpt2 = min (È

Deci, lowpt1(v) este cel mai de jos varf (nivel minim) ce poate fi atins din v, traversand zero sau mai multe muchii de avans, si o singura muchie de intoarcere (fronds). Lowptt2(v) al doilea cel mai de jos varf atins in acelasi mod(sau v daca nu exista).

Notam cu Adj(v) lista de adiacenta ordonata (non-ciclica) a unui nod v, si cu D(v) multimea descendentilor lui v. Cautam o numerotare a nodurilor si o ordonare a muchiilor din listele de adiacenta ce indeplinesc proprietatile urmatoare:

(P1)  radacina lui P este 1.

(P2) daca v V si w₁, w₂, , w_n sunt copiii lui v in P conform ordonarii din Adj(v), atunci w_i = w + |D(w_i+1) . D(w_n)| + 1.

(P3) muchiile e din Adj(v) sunt in ordine crescatoare dupa lowpt1(w) daca e = v w, sau dupa w daca e = v - w.

Fie w₁, w₂, , w_n copiii lui v cu lowpt1(w_i) = u in ordinea data de Adj(v). Atunci exista un i₀ astfel incat lowpt2(w_i) < v pentru 1 i i₀, si lowpt2(w_j) v pentru i₀ < j n.

Daca v - u E', atunci v - u intra in Adj(v) intre v w_i0 si v w_i0+1.

Este aratat in [15] cum se creaza o asemenea numerotare a nodurilor si ordonare a listelor de adiacenta in timp liniar. Spre deosebire de [15], este necesar ca un frond v - w, daca este continut in E', sa intervina intre v w_i0 si v w_i0+1 in Adj(v). Asta se poate face usor adaptand functia de sortare folosita in [15]:

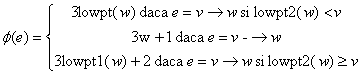
Ordonarea necesara se poate obtine sortand muchiile dupa valorile lor folosind bucket sort. Folosind ordonarea si procedura PATHSEARCH dupa cum e sugerat in [15] nu se vor putea recunoaste toate muchiile multiple si asadar nu se vor putea identifica corect componentele split ale lui G'.

Prespunem ca efectuam o cautare DFS pe G' folosind ordonarea muchiilor din listele de adiacenta. Asta il imparte pe G' intr-o multime de drumuri alcatuite din zero sau mai multe arce urmate de un frond. Primul drum incepe cu nodul 1 si un drum se termina cand primul frond al drumului este intalnit (vezi Fig. 1). Fiecare drum se termina in cel mai mic nod posibil, si are numai primul si ultimul nod in comun cu drumurile traversate anterior. Din fiecare drum de acest fel p : v Þ w, putem forma un ciclu prin adaugarea drumului de la w v la p (compara [15] [16]).

Exemplul 1. Fig. 1 arata un palm tree cu o numerotare care satisface (P1)-(P3). Muchiile sunt numerotate conform drumurilor generate. Drumurile generate sunt

Mai avem nevoie doar de o definitie: u_n este un prim descendent al lui u₀ daca u₀ u_n si fiecare u_i u_i+1 este o prima muchie in Adj(u_i). Mai departe, consideram un palm tree P ce indeplineste conditiile (P1)-(P3). Urmatoarea lema ne da trei conditii usor de verificat pentru perechile de separare.

Lema 3. (Lema 13 in [15]) Fie G = (V, E) un graf biconex si a, b doua noduri din G cu a < b. Atunci este o pereche de separare daca si numai daca una din urmatoarele conditii este adevarata.

Cazul tipului 1: Exista nodurile distincte r a, b si s a, b astfel incat b r, lowpt1(r) = a, lowpt2(r) b, iar s nu este un descendent de-al lui r.

Cazul tipului 2: Exista un nod r b astfel incat a r b, b este un prim descendent al lui r, a 1, fiecare frond x - y cu r ≤ x < b are a ≤ y si fiecare frond x - y cu a < y < b si b w x are lowpt1(w) a.

Cazul mulchiei multiple: (a, b) este o muchie multipla a lui G si G contine cel putin patru muchii.

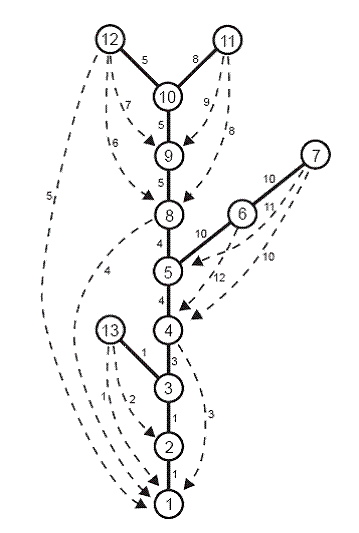
Fig. 1. Palm tree cu noduri numerotate si drumuri generate.

Exemplul 2. Consideram palm tree-ul din Fig. 1. Avem urmatoarele perechi de separare:

perechi de tipul 1: (1, 4), (1, 5), (4, 5), (1, 8), (1, 3)

perechi de tipul 2: (4, 8), (8, 12)

4.3. Identificarea componentelor split

Pe parcursul algoritmului vom pastra un graf G_c si un palm-tree P_c de la G_c. Vom nota cu deg(v) gradul lui v in G_c, cu v→w un arc in P_c, cu v -→w un frond in P_c, cu tatal(v) parintele lui v in P_c. De fiecare data cand identificam o componenta split C, o impartim si G_c si P_c sunt reactualizate. Vom folosi urmatoarele functii pentru update:

C:=new_component(e₁, , e_l): o noua componenta C = este creata si e₁, , e_l sunt scoase din G_c

C:=C: muchiile e₁, ,e_l sunt adaugate in Csi scoase din G_c

e':=new_virtual_edge(v,w,C : o noua muchie virtuala e'=(v,w) este creata si adaugata componentei C si G_c

Vom defini si functiile de acces :

firstChild(v primul fiu al lui v din P_c conform lui Adj(v)

high(w)= , unde F(w) =

Vom folosi si doua stive pentru care sunt definite functiile clasice push, pop si top

ESTACK contine muchiile deja vizitate care nu au fost atribuite unei componente split inca

TSTACK contine tripletele(h,a,b) (sau un marcaj special de sfarsit de stiva - EOS), astfel incat este o pontentiala pereche de sperarare de tip 2, iar h este nodul cu numarul cel mai mare din componenta ce va fi impartita.

Algoritmul incepe prin a apela recursiv procedura PathSearch pentru nodul 1, radacina lui P. Cand se va intoarce din apel, muchiile care apartin componentei split vor fi in ESTACK.

TSTACK.push(EOS);

PathSearch(1);

fie e₁, , e_l muchii in ESTACK

Procedura PathSearch este aratata in Algoritmul 4. Testarea perechiilor de separare prin aplicarea Lemei 3 este ilustrata separat in Algoritmul 5 pentru tipul 2 si Algoritmul 6 pentru tipul 1 de perechi de separare (algoritmul nu va gasi toate perechiile, dar doar pe acelea de care este nevoie la impartirea grafului in componentele split). Pentru a atinge timpul liniar, vom avea nevoie de urmatoarele structuri de date:

palm tree P este reprezentata de vectorii PARENT[v], TREE_ARC[v] (arcul de arbore care intra in v) si TYPE[e] (arc de arbore sau frond);

valorile lowpt1(v), lowpt2(v) si ND(v) sunt precalculate. Nu este nevoie sa le reactualizam;

un vector DEGREE[v] contine gradul lui vG_c. Este reactualizat de fiecare data cand o muchie este adaugata sau scoasa din G_c;

pentru a calcula firstChild(v), vom reactualiza lista de adiacenta de fiecare data o muchie este adaugata sau scoasa din G_c;

pentru a calcula high(v), vom precalcula lista de frond v_i -→ w care se termina in w in ordinea in care sunt vizitate. Cand un frond este scos sau adaugat din G_c, lista respectiva este reactualizata;

vom preclacula un vector START[e] care este true daca si numai daca e incepe un drum;

testul daca "v este adiacent sau nu vizitat inca" de la linia 6.1 poate fi rezolvat pur si simplu numarand arcele adiacente vizitate din arbore.

5. Corectii la algoritmul lui Hopcroft si Tarjan

Procedura SPLIT din [15] nu imparte corect un graf in componente split. Vom rezuma schimbarile pe care le-am facut in algoritmul nostru:

functia de sortare a fost modificata cum este descris in subsectiunea 4.2 pentru a satisface muchiile multiple

crearea ultimei componente split (linia 3.1) lipsea;

conditia de la linia 4.1 a fost schimbata. Conditia originala putea sa elimine triplete din TSTACK corespunzatoare perechilor de separare de tip 2 reale. O astfel de pereche de separare nu putea fi recunoscuta de procedura originala SPLIT;

conditia de la linia 6.1 a fost modificata. Conditia originala putea sa identifice eronat perechi de separare dupa ce graful a fost modificat;

reactualizarile pentru firstChild(v) (care este A1(v) in [15]) si DEGREE(v) nu erau suficiente

high(w) ( care e HIGHPT(w) in [15]) nu era reactualizat, ceea ce nu e corect. HIGHPT trebuie reactualizat dinamic, atunci cand G_c este modificat. Am inlocuit HIGHPT(w) printr-o lista de frond care se termina cu w, care este reactualizata pe masura ce G_c este modificata.