PROIECT DE PLDN

UNIVERSITATEA "DUNAREA DE JOS" DIN GALATI

FACULTATEA STIINTA CALCULATOARELOR

SPECIALIZAREA CTI

PROIECT DE PLDN

Cerinte

Sa se minimizeze functia : f A+B)*(C'+D) + A'B + A'CD si sa se implementeze cu porti logice de tip SI, SAU, NU, SI-NU, SAU-NU, utilizand un numar minim de porti si circuite integrate.

Aspecte teoretice

Algebra booleana

Axiome si teoreme:

Fie o multime M compusa din elementele x₁, x₂,.x_n, impreuna cu operatiile si +. Aceasta multime formeaza o algebra daca:

Multimea M contine cel putin 2 elemente distincte x₁ x₂ (x₁,x₂I M);

Pentru x₁ I M, x₂ I M avem:

x₁ + x₂ I M si x₁ x₂ I M

Operatiile si + au urmatoarele proprietati:

a.       sunt comutative

x₁ x₂ = x₂ x₁

x₁ + x₂ = x₂ + x₁

b.      sunt asociative

x₁ (x₂ x₃) = (x₁ x₂) x₃

x₁ + (x₂ + x₃) = (x₁ + x₂) + x₃

c.       sunt distributive una fata de cealalta

x₁ (x₂ + x₃) = x₁ x₂ + x₁ x₃

x₁ + (x₂ x₃) = (x₁ + x₂) (x₁ + x₃)

Ambele operatii admit cate un element neutru cu proprietatea:

x₁ + 0 = 0 + x₁ = x₁

x₁ x₁ = x₁

unde 0 este elementul nul al multimii, iar 1 este elementul unitate al multimii.

Daca multimea M nu contine decat doua elemente, acestea trebuie sa fie obligatoriu elementul nul 0 si elementul unitate 1; atunci pentru x I M exista un element unic notat cu x cu proprietatile:

x x = 0 principiul contradictiei

x + x = 1 principiul tertului exclus

x este inversul elementului x.

In definirea axiomatica a algebrei s-au folosit diferite notatii. In tabelul urmator se dau denumirile si notatiile specifice folosite pentru diverse domenii:

Proprietatile algebrei booleene

Plecand de la axiome se deduc o serie de proprietati care vor forma reguli de calcul in cadrul algebrei booleene. Aceste proprietati sunt:

Principiul dublei negatii

x = x dubla negatie duce la o afirmatie

Idempotenta

x x = x

x + x = x

Absorbtia

x₁ (x₁ + x₂) = x₁

x₁ + (x₁ x₂) = x₁

Proprietatile elementelor neutre

x x 1 = x

x + 0 = x x + 1 = 1

Formulele lui De Morgan

x₁ x₂ = x₁ + x₂

x₁ + x₂ = x₁ x₂

Aceste formule sunt foarte utile datorita posibilitatii de a transforma produsul logic in suma logica si invers.

Formulele pot fi generalizate la un numar arbitrar de termeni:

x₁ x₂ x_n  = x₁ + x₂ + . + x_n

x₁ + x₂ + . + x_n = x₁ x₂ x_n

Principiul dualitatii - daca in axiomele si proprietatile algebrei booleene se interschimba 0 cu 1 si + cu , sistemul de axiome ramane acelasi, in afara unor permutari.

Verificarea proprietatilor se poate face cu ajutorul tabelelor de adevar si cu observatia ca doua functii sunt egale daca iau aceleasi valori in toate punctele domeniului de definitie. Prin tabelul de adevar se stabileste o corespondenta intre valorile de adevar ale variabilelor si valoarea de adevar a functiei.

Obs. Comutativitatea si asociativitatea pot fi extinse la un numar arbitrar, dar finit, de termeni, indiferent de ordinea lor.

METODA VEITCH-KARNAUGH

Metoda Veitch-Karnaugh pentru forma minima disjunctiva presupune: construirea diagramei Veitch-Karnaugh, gruparea celulelor vecine pentru care functia ia valoarea '1' si eliminarea variabilelor ce isi schimba valoarea in cadrul aceleasi grupari. Fiecare celula ocupata de '1' trebuie sa faca parte din cel putin o grupare, dar poate fi inclusa in mai multe grupari.

Minimizarea incepe prin gruparea celulelor vecine cate doua. Daca un grup de doua celule vecine este vecin la randul sau cu un alt grup de doua celule vecine (cele doua grupuri difera prin valoarea unei singure variabile), acestea se pot contopi intr-un singur grup de patru celule vecine, ceea ce va permite eliminarea a doua variabile. Daca este posibil, procedura descrisa se repeta, obtinandu-se un grup de opt celule vecine etc.

In general, un grup pe 2^m celule vecine ocupate de '1' permite eliminarea a m variabile. Cel mai avansat grad de simplificare se obtine daca valorile '1' dintr-o diagrama Karnaugh sunt grupate intr-un numar minim de grupuri, fiecare grup continand un numar maxim de '1'. Procedura expusa este similara pentru determinarea formei minime conjunctive, cu observatia ca rolul lui '1' este jucat de '0'. In cazul functiilor incomplet definite, valorile indiferente ale functiei se considera '1' pentru forma disjunctiva si '0' pentru forma conjunctiva daca aceste valori participa la minimizare; valorile indiferente care nu sunt prinse in grupari devin '0' pentru forma disjunctiva si '1' pentru forma conjunctiva. Prin participarea valorilor indiferente la minimizare se pot elimina mai multe variabile.

Motivatia alegerii Diagramei Veitch

Am ales aceasta schema pentru ca e mai usor de observat modul de grupare a elementelor :

Functia este: f A+B)*(C'+D) + A'B + A'CD

Notam cu a=AB'+BC'+CD'

b= AC'(AB'+BC'+CD')

c CD'+AB)'

Minimizarea functiei se realizeaza cu ajutorul diagramei Veitch care are urmatoarea reprezentare:

Diagrama Veitch a functiei f este urmatoarea:

In urma gruparii va rezulta functia minimizata: f'= A'B'C' + A'B'D' + ACD'.

Reprezentarea prin porti logice este urmatoarea:

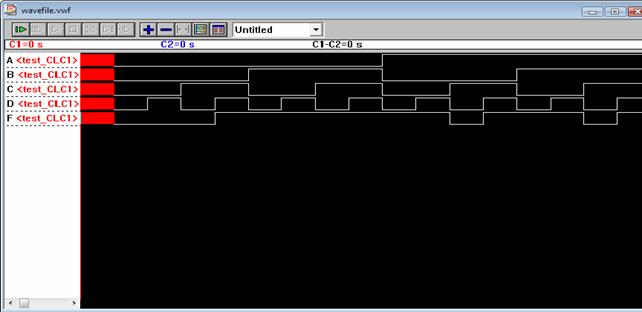
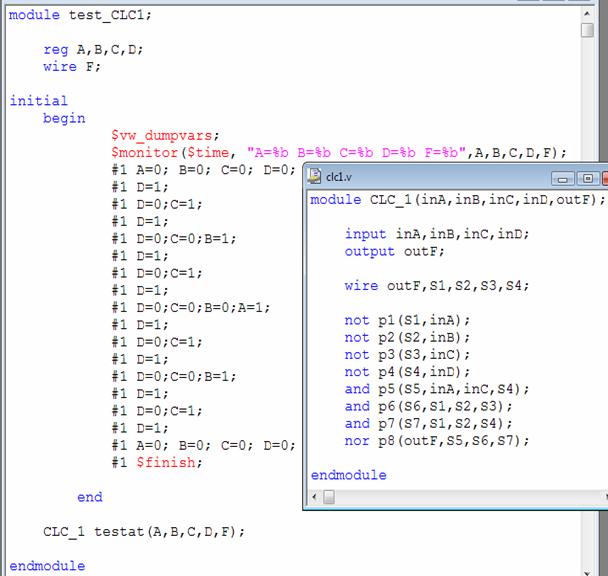SIMULARE

BIBLIOGRAFIE

Rustem POPA - "Curs de ASDN"

www.google.ro

ANEXE

Tipuri de circuite integrate folosite :

Poarta SI cu 3 intrari : 7411

Poarta SAU-NU cu 3 intrari : 4075

Inversoare : 7404