Teoria Grafurilor - Drumuri de cost minim

Universitatea "Lucian Blaga ", Sibiu 

Facultatea de Stiinte, Domeniul Matematica

Profil Matematica-Informatica, 2007

Teoria Grafurilor :

Drumuri de cost minim

Cuprins

1. Introducere in Grafuri

Problema celor 7 poduri din Knigsberg

Exemple

Drumuri in grafuri

Matricea Costurilor

2. Problema drumurilor minime cu origine unica

Algoritmul lui Djikstra

3. Poblema drumurilor minime   corespunzatoare tuturor perechilor de noduri

Algoritmul lui Floyd

4. Bibliografie

In lucrare sunt prezentati algoritmii lui Dijkstra si Floyd pentru gasirea cailor de cost minim intre doua noduri precizate, respectiv intre oricare doua noduri ale unui graf.

1.Introducere in Grafuri

1.1.Problema celor 7 poduri din Knigsberg (Kalingrad)

Aceasta banala si totusi foarte controversata problema a dus la aparitia si dezvoltarea teoriei grafurilor.

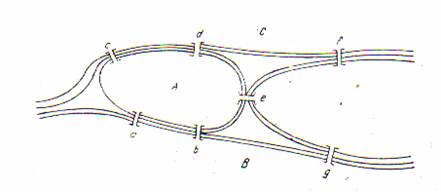
Orasul Knigsberg era asezat pe coasta Marii Baltice, la gurile raului Pregel. Pe rau erau doua insule legate de tarmuri si intre ele de sapte poduri ca in

figura 4.

Fig. 4

Oamenii care cutreierau aceste insule au observat ca daca porneau de pe malul sudic al raului, nu puteau sa-si planifice plimbarea astfel incat sa traverseze fiecare pod o singura data. Se parea ca ori trebuia sa sara un pod ori sa-l traverseze de doua ori.

In anul 1735 Leonhard Euler (1707-1783, matematician si fizician elvetian) a analizat si rezolvat problema din punct de vedere matematic iar in 1736 a scris prima lucrare de teorie a grafurilor despre problema acestor sapte poduri.

In viata de zi cu zi rezolvam adesea, fara sa ne dam seama probleme de grafuri euleriene, de exemplu cand vrem sa mergem cu trenul in circuit si vrem sa platim mai putin, calculam in asa fel incat sa trecem peste tot si sa platim mai putin. Dar aceasta nu o facem numai noi si postasii, ci grafurile se utilizeaza la calcularea pozitilor optime de amplasare a satelitilor de comunicatie pentru ca informatia transmisa sa foloseasca putin timp, caci "time is money".

In matematica si informatica, teoria grafurilor studiaza proprietatile grafurilor. Un graf este o multime de obiecte (numite noduri) legate intre ele printr-o multime de muchii carora le pot fi atribuite directii (in acest caz, se spune ca graful este orientat). Vizual, un graf poate fi reprezentat ca o multime de puncte legate intre ele prin linii (de obicei curbe).

Cu alte cuvinte grafurile modeleaza sisteme de obiecte si legaturile lor.

1.2. Exemple:

Hemoglobina Circuit

Grafurile au o importanta imensa in informatica, de exemplu:

• in unele problemele de sortare si cautare - elementele multimii pe care se face sortarea sau cautarea se pot reprezenta prin noduri intr-un graf;

• schema logica a unui program se poate reprezenta printr-un graf orientat in care o instructiune sau un bloc de instructiuni este reprezentat printr-un nod, iar muchiile directionate reprezinta calea de executie;

• in programarea orientata pe obiecte, ierarhia obiectelor (claselor) unui program poate fi reprezentata printr-un graf in care fiecare nod reprezinta o clasa, iar muchiile reprezinta relatii intre acestea (derivari, agregari).

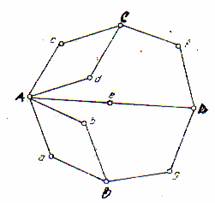
Numim graf o pereche ordonata de multimi, notata G=(N,A), unde N este o multime finita si nevida de elemente numite noduri sau varfuri, iar A este o multime de perechi (ordonate sau neordonate) de elemente din N numite muchii (daca sunt perechi neordonate) sau arce (daca sunt perechi ordonate). In primul caz, graful se numeste orientat - fig2, altfel acesta este neorientat- fig 1.

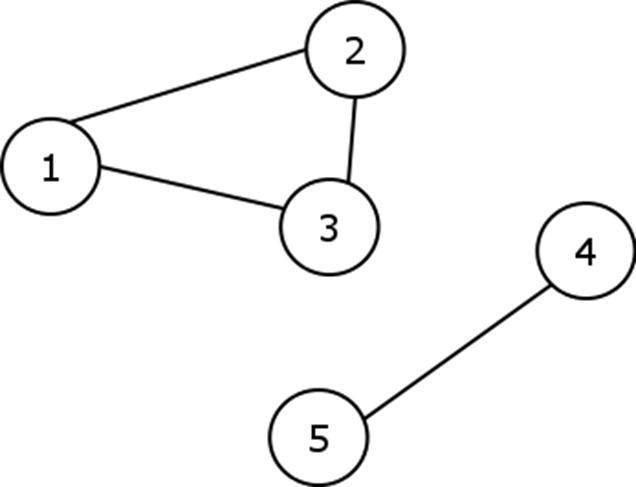
Fig 1. Graf Neorientat

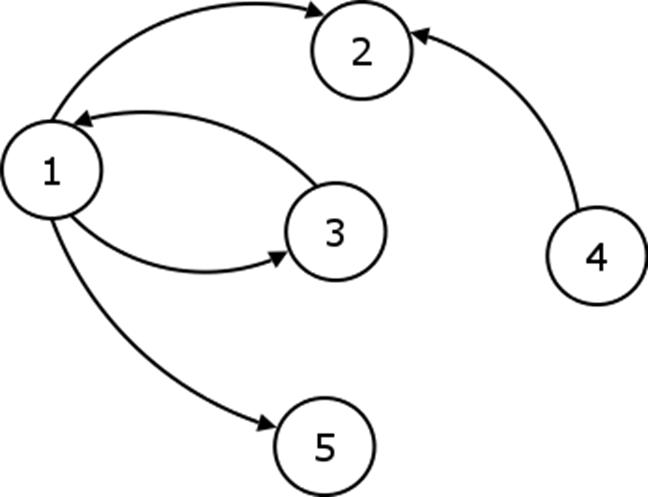
Fig 2. Graf Orientat

Asadar un graf poate fi reprezentat sub forma unei figuri geometrice alcatuite din puncte (care corespund varfurilor) si din linii drepte sau curbe care unesc aceste puncte (care corespund muchiilor sau arcelor).

Spunem ca un nod v este incident cu o muchie r daca . Doua varfuri x si y se numesc adiacente daca exista o muchie e care le uneste (cu care amandoua varfurile sunt incidente). Doua muchii sunt adiacente daca exista un nod x care sa fie incident cu ambele muchii.

1.3. Drumuri intr-un Graf

Un drum in graful G=(N,A) este o succesiune de noduri cu proprietatea ca , sunt arce perimise in G. Nodurile si sunt extremitatile drumului .

Un drum se numeste simplu daca muchiile care il compun sunt distincte. Numim ciclu un drum care are drept capete un acelasi varf.

Daca P = x₀, , x_k-1 este un drum in graful G si x_k-1x₀ este o muchie in acest graf, atunci P + x_k-1x₀ este un ciclu din graful G, adica este o cale de la varf la el insusi.

Un ciclu se numeste hamiltonian daca este simplu si trece prin toate nodurile grafului G, exact o data, si se numeste eulerian daca trece prin toate muchiile grafului G, exact o data. Nu orice graf contine un ciclu hamiltonian (Fig. 2).

Spunem ca G' este un subgraf al lui G, daca acesta contine o parte din varfurile lui G si numai acele muchii care le conecteaza; G'=(N',A') este subgraf al lui G=(N,A) , daca N'N si A'A.

Spunem ca un graf este conex daca intre oricare doua varfuri ale acestuia exista cel putin un drum.

Un graf este ponderat daca in cadrul sau fiecarui arc ii este asociata o valoare.

Complementul unui graf G este graful ,care contine o muchie intre varfurile x si y daca si numai daca G nu contine o astfel de muchie.

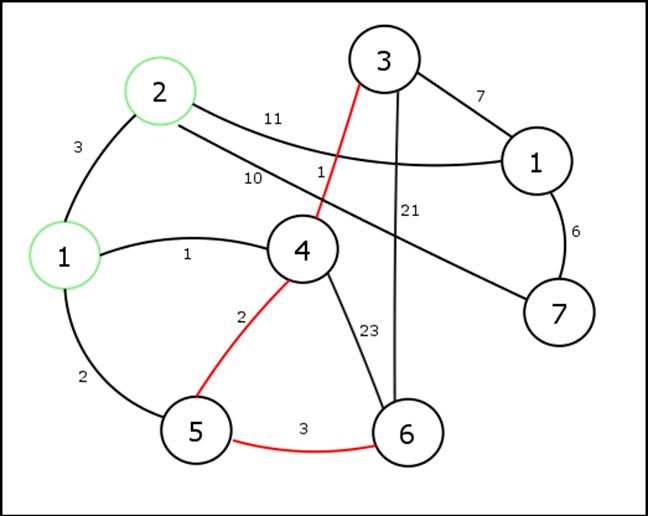
Fig 3. Graf Complex: Varfurile verzi sunt adiacente
Muchiile rosii formeaza un drum care leaga nodurile 3 si 6

1.4. Matricea costurilor

Consideram un graf orientat G=(N,A) cu n noduri, in care fiecarui arc ii este asociat un numar intreg numit cost. Semnificatia acestui cost poate fi foarte variata, in functie de domeniul pe care il descrie graful. De exemplu, daca graful reprezinta harta unui oras in care arcele sunt strazile iar nodurile sunt intersectiile dintre strazi, atunci putem vorbi despre costul deplasarii unui automobil intre doua intersectii, de-a lungul unei strazi. Acesta s-ar putea masura in cantitatea de benzina consumata, calculata prin prisma lungimii strazii in m sau in km.

Pentru evidentierea costurilor tuturor arcelor unui graf cu n noduri se poate defini o matrice a, cu n linii m coloane. exista doua forme ale acestei matrici:

Forma a): Fiecare element a[i,j] poate fi:

-c, daca exista un arc de cost c>0 intre nodurile i si j;

-0, daca i=j

- , daca nu exista arc intre nodurile i si j.

Forma b): Este absolut similara, cu singura deosebire ca in loc de + avem -

Forma a)se foloseste pentru determinarea drumurilor de cost minim intre doua noduri, iar forma b) este utilizata in aflarea drumurilor de cost maxim.

Problema determinarii drumului minim intre doua noduri face obiectul algoritmelor urmatore:

2.Problema drumurilor minime cu origine unica

Algoritmul lui Dijkstra

Se considera un graf orientat ponderat, G=(N,A), fiecarui arc a=(i,j) din A ii este asociat un cost COST[i,j].

Algoritmul utilizeaza o structura de date multime M in care mentine nodurile din N pentru care cea mai scurta distanta pana la nodul origine e deja cunoscuta. Aceasta multime M corespunde mult imii nodurior 'vizitate' deja. M se initializeaza cu nodul de start.

Algoritmul cuprinde mai multe iteratii, in cadrul fiecarei iteratii se selecteaza un nod x din multimea N-M, cu proprietatea ca x este cel mai aproape de nodul de start si se trece in multimea M a nodurilor vizitate. Se verifica apoi pentru fiecare nod y ramas in N-M daca nu exista un drum mai scurt de la nodul origine spre y, drum care trece prin x.

Algoritmul utilizeaza un tablou D, D[i] fiind lungimea celui mai scurt drum de la origine la nodul numarul i la un moment dat. Initial, D[i]=COST[origine,i]. Pe masura ce se gasesc noduri x,y astfel incat D[y]>D[x]+COST[x,y], D[y] este redus. La terminarea algoritmului, D[i] va contine lungimea drumului minim de la origine la i.

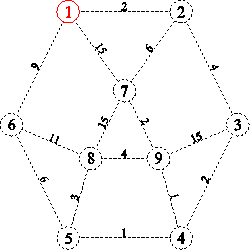
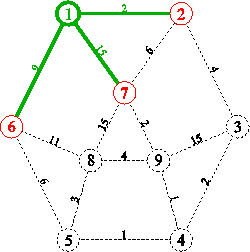
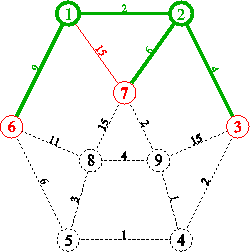
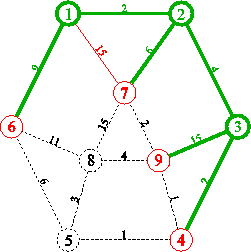
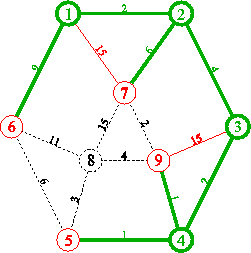
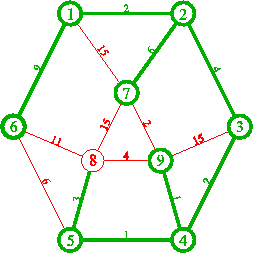
procedure Dijkstra;


begin
* initializeaza multimea M a nodurilor vizitate, introduce nod_origine in M
* pentru toate nodurile i, initializeaza lungimea drumului minim pana la i
(D[i]) cu lungimea arcului direct de la nod_origine la i
while ( * mai exista noduri in N-M ) do
begin
* alege un nod x apartina nd multimii N - M astfel i ncat D[x]
sa fie minim si il adauga pe x la M;
for * fiecare nod y din N-M do
* test daca drumul de la nod_origine la y folosind ca punct intermediar nodul x
este mai scurt decit cel memorat anterior, si daca da, actualizeaza D[y]
in forma D[y] := min(D[y],D[x] + COST[x,y]);
end
end;

Exemplu:

1.

2.

3.

4.

5.

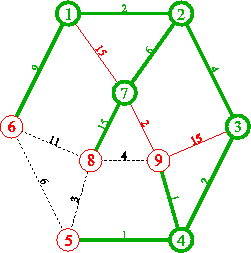
6.

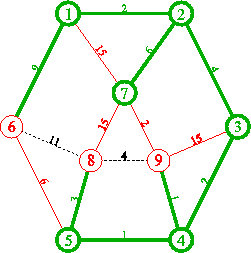
7.

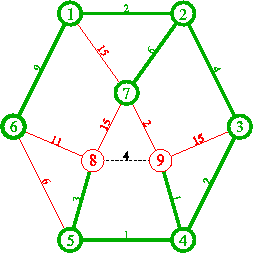
8.

9.

10.

3.Problema drumurilor minime corespunzatoare tuturor perechilor de noduri.

Algoritmul lui Floyd

Se considera un graf orientat G=(N,A), in care fiecare arc a=(i,j) din A are o pondere pozitiva COST[i,j]. Problema drumurilor minime corespunzatoare tuturor perechilor de noduri presupune determinarea, pentru fiecare pereche ordonata (i,j), a lungmii drumului minim care conecteaza i cu j.

O rezolvare a acestei probleme este aplicarea repetata a algoritmului lui Dijkstra avand ca nod origine fiecare nod al grafului.

O alta metoda de rezolvare directa a acestei probleme este data de algoritmul lui Floyd.

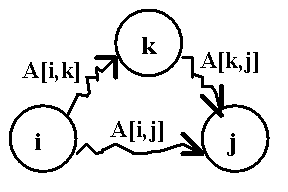
Algoritmul utilizeaza o matrice A de dimensiuni NxN, in care A[i,j] va fi lungimea drumului minim de la i la j. Initial, se presupune ca drumul minim de la i la j este arcul (i,j). Se testeaza apoi fiecare nod k al grafului, pentru a vedea daca pentru fiecare pereche de noduri i,j nu exista un drum mai scurt de la i la j trecand prin k (figura 1), adica daca suma drumurilor minime de la i la k s i de la k la j nu este mai mica decat drumul considerat minim de la i la j.

Pentru a determina traseele drumurilor minime, se poate introduce o matrice Drum de dimeniune NxN, Drum[i,j] memoreaza acel nod k care conduce i n cadrul algoritmului la scurtarea drumului A[i,j]. Se va alege o valoare speciala pentru 'nod inexistent'. Daca Drum[i,j]=nod inexistent, atunci cel mai scurt drum de la i la j este arcul direct.

procedure Floyd;


begin
* init ializeaza matricea lungimilor drumurilor minime A[i,j]) si matricea
nodurilor intermediare de pe trasee (Drum[i,j]) presupunand ca drumul minim
intre oricare doua noduri este arcul direct
for * fiecare nod k al grafului do
for * fiecare pereche de noduri i,j do
if (* suma drumurilor de la i la k s i de la k la j e mai mica decat drumul de la
i la j ( A[i,k] + A[k,j] < A[i,j] )) then
begin
* actualizeaza valoarea drumului minim, prin A[i,j] := A[i,k] + A[k,j]
* memoreaza punctul de pe traseu, Drum[i,j] := k
end
end;

Pentru reconstituirea traseelor, se poate folosi urmatorul algoritm recursiv. Algoritmul afiseaza traseul drumului minim intre intre doua noduri specificate, nodurile i si j.

procedure Traseu(i,j:integer);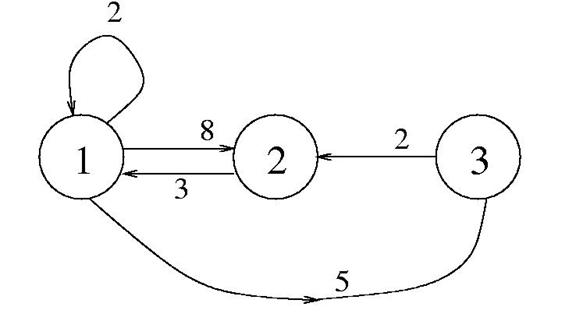


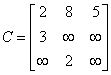
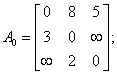
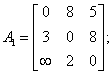
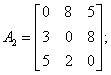
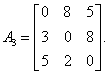
begin
if ( *exista cel putin un nod k=Drum[i,j] intermediar de la i la j)
then
begin
Traseu(i,k);
writeln(k);
Traseu(k,j);
end;
end;




daca
daca
Notam daca nu e arc direct de la i la j.





Exemplu:

4. Bibliografie

1.https://de.wikipedia.org/wiki/Leonhard_Euler

2.https://www.inf.fh-flensburg.de/lang/algorithmen/grundlagen/graph.htm

3. "Drumuri minime cand costurile sunt mici"-Mircea Digulescu,Andrei Matei (Focus-GInfo nr 136 octombrie 2003)

4. https://www2.informatik.hu-berlin.de/alkox/lehre/skripte/ga/

5. "Grafuri orientate aplicatii" ing.Ciprian Chirila

6. https://www.zaik.uni-koeln.de/AFS/teachings/courses/Graph/skript/Kapitel3.pdf