Algoritmi de cautare, interclasare, sortare, selectie

Adeseori in programare se pune problema regasirii unui element sau a ordonarii componentelor unei colectii de date dupa un anumit criteriu. Pentru ca in practica exista o varietate foarte mare de colectii de date care sunt prelucrate -varietate exprimata fie prin volumul colectiei, fie prin organizarea datelor ei, fie prin complexitatea articolelor care o compun- s-a impus crearea mai multor algoritmi care sa rezolve problemele de mai sus. Chiar daca exista mai multi algoritmi care rezolva aceeasi problema, fiecare are particularitatile sale, iar alegerea unuia dintre ei se face in functie de natura problemei concrete ce trebuie rezolvata.

Inainte de a trece mai departe, sa precizam cateva lucruri despre notiunea de ordine in colectiile de date. O colectie de date este o multime de elemente, fiecare element fiind descris printr-unul sau mai multe campuri (proprietati), dintre care numai un singur camp, numit cheie, va controla forma de organizare a datelor colectiei. Putem vorbi despre operatii de cautare, sortare samd. cata vreme pe multimea cheilor colectiei de date este definita o relatie de ordine (totala sau partiala).

Spunem ca o multime de elemente este total ordonata (sau ordonata liniar) dupa relatia de ordine "<" daca intre oricare trei elemente ale sale se verifica proprietatile:

legea trihotomiei: are loc exact una si numai una dintre cele trei posibilitati: a<b sau b<a sau a=b.

tranzitivitatea: daca a<b si b<c, atunci a<c.

Cea mai mare parte a algoritmilor prezentati in aceasta sectiune se aplica masivelor intre ale caror elemente exista relatii totale de ordine, va fi insa studiata si o metoda de sortare pe multimi partial ordonate-sortarea topologica.

Din punctul de vedere al timpului de calcul, in problemele de cautare, sortare, selectie, interclasare se considera, de regula, ca operatie de baza comparatia (sau, acolo unde este cazul, testarea egalitatii) ce implica elemente ale masivului.

Fara a restrange generalitatea, in exemplele care urmeaza am considerat ca articolele colectiei de date contin o singura informatie, cheia, care este de tip intreg. In practica insa elementele pot avea structuri mult mai complexe.

I.1          Cautari

Algoritmii de cautare presupun identificarea pozitiei pe care se afla o cheie data intr-un masiv. De regula, functiile de cautare intorc pozitia in masiv a primei aparitii a elementului cautat (in C: 0, 1, 2 n-1, pentru un masiv de dimensiune n) in caz de succes, sau un numar in afara intervalului daca elementul nu se afla in masiv (de exemplu -1). In functie de organizarea datelor unei colectii si de modul de cautare, distingem trei metode:

• Cautarea secventiala - este utilizata atunci elementele masivului se afla intr-o ordine arbitrara;
• Cautarea binara - este o cautare optimizata care se utilizeaza atunci cand masivul de date este sortat;
• Arbori de cautare - sunt construiti pentru a atinge performante de cautare comparabile cu cele ale cautarii binare, dar care pot fi utilizati pentru colectii de date nu neaparat sortate.

I.1.1         Cautarea secventiala (liniara)

Cautarea liniara consta in parcurgerea secventiala a masivului de date si verificarea pentru fiecare element daca este cel cautat. Daca, la un moment dat, elementul a fost gasit, atunci procesul de cautare se opreste.

Cautarea secventiala

#include<iostream.h>

int LSearch(int A[], int n, int e)

main()

int n=sizeof(A)/sizeof(*A);

int e=7;

int poz= LSearch (A, n, e);

if(poz==-1) cout<<e<<' nu se afla in masiv';

else cout<<e<<' se afla pe pozitia '<<poz;

return 0;

Observatie: Variabila booleana a fost utilizata pentru a opri cautarea atunci cand numarul a fost gasit.

In algoritmul de mai sus, operatia de baza va fi comparatia-testarea egalitatii ce implica elemente ale masivului. Aceasta operatie se efectueaza de n ori in caz de esec (pentru a se constata ca elementul cautat nu se afla in vector trebuie parcurs vectorul in intregime), sau cel mult n comparatii, in caz de succes. Asadar, numarul maxim de comparatii este n, deci timpul maxim este O(n).

Numarul mediu de comparatii in cazul cautarii cu succes se evalueaza luand in calcul toate posibilitatile. Avem n situatii posibile: daca elementul cautat este pe prima pozitie, atunci se efectueaza o singura comparatie, daca se afla pe cea de-a doua pozitie, avem doua comparatii, , daca se afla pe ultima pozitie, avem n comparatii, asadar (1+2++n)/n comparatii, adica n*(n+1)/(2*n)=(n+1)/2. Si in cazul estimarii timpului mediu, am obtinut tot O(n).

In concluzie, algoritmul de cautare secventiala este un algoritm liniar (polinomial de ordin 1), care nu necesita memorie suplimentara.

I.1.2         Cautarea binara

Cautarea binara este o metoda de cautare optimizata, care are la baza metoda de programare Divide et Impera si care pleaca de la ipoteza ca vectorul de date este sortat.

Metoda este similara unui joc de copii, prin care un copil trebuie sa ghiceasca un numar intre 1 si 100 scris de catre un alt copil pe o foaie de hartie. Primul copil are posibilitatea sa incerce diferite valori, la fiecare incercare el primeste raspunsul "mai mic" sau "mai mare", pana cand ghiceste numarul. Este evident ca alegerea de fiecare data a jumatatii intervalului de cautare si reducerea cautarii astfel pe un interval de doua ori mai mic, va minimiza numarul de incercari. Astfel, prima incercare va fi 50, daca la ea se va raspunde cu "mai mare", cautarea va continua pe intervalul 51-100, daca se va raspunde cu "mai mic", cautarea va continua pe intervalul 1-49 samd.

Cautarea binara functioneaza dupa urmatorul procedeu: se compara elementul cautat, fie e acesta, cu cel din mijlocul vectorului. Avem trei posibilitati:

cele doua valori coincid - in acest caz elementul dat a fost gasit si se incheie cautarea;

elementul cautat este mai mic decat cel aflat pe pozitia centrala in vector - in acest caz se repeta cautarea pe prima jumatate a vectorului;

elementul cautat este mai mare decat cel aflat pe pozitia centrala in vector - atunci se va repeta cautarea in cea de-a doua jumatate a vectorului.

Algoritmul se incheie cand fie am gasit elementul (cautare cu succes), fie cautarea s-a redus la un interval de lungime 0, ceea ce inseamna ca elementul nu se afla in vector.

Datorita naturii recurente a procedeului de mai sus, vom elabora o solutie recursiva pentru cautarea binara.

Cautarea binara

#include<iostream.h>

int BSearch(int A[], int p, int u, int e)

main()

int n=sizeof(A)/sizeof(*A);

int e=5;

int poz=BSearch(A, 0, n-1, e);

if(poz==-1) cout<<e<<' nu se afla in masiv';

else cout<<e<<' se afla pe pozitia '<<poz;

return 0;

Pentru o problema de dimensiune 2^k-1 <=n< 2^k (vectorul este de dimensiune n) avem in cazul cel mai defavorabil cel mult k injumatatiri ale intervalului, ceea ce inseamna k comparatii, asadar algoritmul de cautare binara are timpul de calcul de ordin O(log₂n).

I.1.3         Arbori de cautare

Arborii binari de cautare au fost deja prezentati in sectiunea dedicata arborilor. Reamintim ca, prin definitie, ei au particularitatea urmatoare: cheia oricarui nod tata este mai mare decat oricare cheie din sub-arborele stang (daca exista) si mai mica decat oricare cheie a sub-arborelui drept (daca exista). In aceasta sectiune ne vom opri din nou atentia asupra arborilor de cautare, de aceasta data priviti ca metoda de cautare.

Pentru a putea evalua eficienta arborelui de cautare vom analiza mai intai complexitatea algoritmului de inserare a unui nod in arbore, algoritm elaborat prin tehnica de programare Divide et Impera. Cazul cel mai defavorabil corespunde situatiei cand inserarea fiecarui nod in arbore necesita parcurgerea unui drum de lungime maxima (situatie obtinuta atunci cand, de exemplu, datele de intrare au cheile deja ordonate, crescator sau descrescator, atunci arborele va "creste" intr-o singura directie, numai pe stanga sau numai pe dreapta, degenerand intr-o lista liniara-orice nod are un singur descendent, iar inserarea unui nod nou presupune parcurgerea tuturor nodurilor deja inserate). In acest caz, inserarea primului nod nu necesita comparatii, inserarea celui de-al doilea nod necesita 1 comparatie, inserarea celui de-al treilea nod 2 comparatii, , al n-lea nod necesita n-1 comparatii, in total n*(n-1)/2 comparatii, ceea ce face ca timpul maxim de calcul al algoritmului de inserare sa fie polinomial de ordin O(n²).

Timpul de calcul necesar cautarii unui element intr-un astfel de arbore este comparabil cu cel necesar cautarii binare: O(log₂n), insa utilizarea arborilor de cautare prezinta avantajul ca nu se limiteaza la masive sortate. Din punctul de vedere al memoriei suplimentare, arborii de cautare utilizeaza cate doi pointeri suplimentari pentru fiecare element al masivului.

I.2          Interclasarea

Interclasarea, intalnita in literatura de specialitate si sub denumirea de "fuzionare" sau "colationare", consta in combinarea (concatenarea) a doua masive sortate intr-unul singur, sortat la randul sau.

O solutie de interclasare consta in parcurgerea concomitenta a celor doua masive si preluarea in vectorul destinatie a celui mai mic dintre elementele curente ale masivelor sursa. In momentul in care elementele unuia dintre acestea se termina, elementele neparcurse ale celuilalt vor fi preluate automat.

De exemplu, daca A[]= si B[]=, vom avea succesiv :

Interclasare

#include<iostream.h>

void Interclasare(int A[], int m, int B[], int n, int C[])

main()

B[]=;

int m=sizeof(A)/sizeof(*A),

n=sizeof(B)/sizeof(*B);

int *C=new int[m+n];

Interclasare(A,m,B,n,C);

for(int i=0;i<m+n;i++) cout<<C[i];

delete []C;

return 0;

Operatia de baza folosita in evaluarea complexitatii va fi comparatia intre elementele celor doua masive, care se efectueaza de cel mult m+n-1 ori (in ciclul while), situatie obtinuta atunci cand un vector a fost parcurs in intregime, iar in celalalt a ramas un singur element.

I.3          Strategii generale de sortare (ordonare totala)

Sortarea unei colectii presupune identificarea unei permutari a indicilor sai care sa plaseze elementele colectiei in ordine crescatoare a cheilor. Sortarea elementelor se poate efectua fie fizic, atunci cand, odata sortate, elementele ocupa noile lor pozitii in masiv, fie prin intermediul unei tabele care va contine permutarea corespunzatoare de indici.

Metodele generale de sortare pe care le vom studia au fost impartite in cinci clase, dupa cum urmeaza :

sortarea prin selectie

sortarea prin insertie

a.        directa

b.        binara

sortare prin interschimbare

a.        metoda bulelor

b.        sortare rapida

sortare prin interclasare

sortarea prin numarare

Asa cum vom vedea mai jos, clasele de metode nu sunt foarte clar delimitate, gruparea lor este orientativa. Spre exemplu, sortarea prin insertie directa poate fi privita si ca metoda prim interschimbare, intrucat presupune interschimbarea succesiva a elementului curent cu cele anterioare lui, cata vreme nu sunt in ordinea dorita.

Trebuie mentionat ca toate metodele de sortare generala ce vor fi prezentate, mai putin cea prin numarare, efectueaza interschimbari de elemente ale colectiei de date. In cazul in care cheile (ca si camp) ocupa foarte putin din inregistrarea din care fac parte, interschimbarea elementelor va creste nejustificat timpul de executie. In aceste situatii este indicat fie sa se utilizeze tabele de indici corespunzatoare permutarii masivului sortat, fie ca elementele colectiei sa fie memorate intr-o lista, caz in care procesul de sortare nu va interschimba efectiv elementele (nodurile), ci va modifica numai legaturile dintre acestea.

I.3.1         Sortarea prin selectie

Metoda consta in asezarea succesiva a elementelor pe pozitiile lor finale: se determina minimul vectorului si se interschimba cu primul element, apoi se determina minimul vectorului din care omitem primul element, si se interschimba cu cel de-al doilea element samd. Se repeta procedeul de n-1 ori.

De exemplu, sa consideram vectorul A[]=. Avem:

9 5 4 1 7 10 8 3 6: min

1 9 5 4 2 7 10 8 3 6: min

1 2 5 4 9 7 10 8 3 6: min

1 2 3 4 9 7 10 8 5 6: min

Sortarea prin selectie

#include<iostream.h>

void SelSort(int A[], int n)

}

main()

int n=sizeof(A)/sizeof(*A);

SelSort(A,n);

for(int i=0;i<n;i++) cout<<A[i];

return 0;

Metoda impresioneaza prin simplitatea ei. Din punctul de vedere al complexitatii nu se distinge insa fata de alte metode de sortare. La prima iteratie se efectueaza n-1 comparatii, la a 2-a n-2 comparatii, , la a (n-1)-a iteratie ramane de efectuat o singura comparatie. In total, n*(n-1)/2, cu alte cuvinte algoritmul este in timp polinomial de ordin O(n²).

I.3.2         Sortarea prin insertie

I.3.2.1   Sortarea prin insertie directa

Sortarea prin insertie directa presupune parcurgerea repetata a vectorului si sortarea, la cea de-a i-a parcurgere, a secventei (A₀, A₁, A₂, , A_i) prin inserarea lui A_i pe pozitia corespunzatoare in prefixul (A₀, A₁, A₂, , A_i-1), deja sortat in urma parcurgerilor anterioare: se compara A_i pe rand cu A_i-1, A_i-2, pana cand fie se gaseste un element mai mic decat A_i, caz in care A_i va fi asezat imediat in dreapta lui, fie se termina vectorul, caz in care A_i va fi asezat pe prima pozitie. Toate elementele A_i-1, A_i-2, cu care a fost comparat A_i vor fi deplasate cu o pozitie mai la dreapta. Dupa cel mult n-1 parcurgeri, vectorul va fi sortat.

Pentru simplificarea metodei, vom deplasa elementele A_i-1, A_i-2, la dreapta cu o pozitie imediat dupa ce le comparam cu A_i.

In unele lucrari de specialitate, sortarea prin insertie mai este denumita si "sortare prin scufundare", functionand dupa principiul scufundarii, la fiecare parcurgere, a elementelor cu chei mici pe primele pozitii in masiv.

Mecanismul metodei este urmatorul: sa consideram vectorul A[]=.

Sortarea prin insertie directa

#include<iostream.h>

void InsertSort(int A[], int n)

main()

int n=sizeof(A)/sizeof(*A);

InsertSort(A,n);

for(int i=0;i<n;i++) cout<<A[i];

return 0;

Considerand ca operatie de baza comparatia cu elemente ale vectorului, vom avea in cazul cel mai defavorabil (atunci cand vectorul este ordonat descrescator) n-1 parcurgeri cu 1, 2, respectiv n-1 comparatii. In total, n*(n-1)/2, adica avem un algoritm polinomial de complexitate O(n²).

I.3.2.2   Sortarea prin insertie binara

O imbunatatire a algoritmului de sortare prin insertie directa poate fi obtinuta utilizand tehnica Divide et Impera, intr-un mod similar cautarii binare. Plecand de la prezumtia ca la cea de-a k-a parcurgere a vectorului secventa (A₀, A₁, A₂, , A_k-1) este deja sortata din parcurgerile anterioare, cautarea pozitiei pe care va fi inserat A_k se va face prin injumatatirea intervalului. Vom utiliza in acest sens, functia de cautare binara prezentata mai devreme in acest capitol, usor modificata.

Sortarea prin insertie binara

#include<iostream.h>

int BSearch(int A[], int p, int u, int e)

void InsertBSort(int A[], int n)

main()

int n=sizeof(A)/sizeof(*A);

InsertBSort(A,n);

for(int i=0;i<n;i++) cout<<A[i];

return 0;

Asa cum am aratat, algoritmului de cautare binara intr-un masiv ordonat de dimensiune n ii corespunde un timp de calcul de ordin O(log₂n). Asadar, cautarea pozitiei pe care va fi inserat elementul curent A_k in secventa (A₀, A₁, A₂, , A_k-1) necesita O(log₂k) comparatii. Cum k ia valori de la 1 la n-1, vom avea . Cum , asadar algoritmul are un timp de calcul O(nlog₂n)<< O(n²).

I.3.3         Sortarea prin interschimbare

Metodele de sortare prin interschimbare au la baza schimbarea sistematica a perechilor de elemente care nu se afla in ordinea corespunzatoare. Prezentam mai jos doua dintre cele mai cunoscute metode din aceasta categorie.

I.3.3.1   Metoda bulelor (Bubble Sort)

Sortarea prin metoda bulelor consta in parcurgerea repetata a vectorului si interschimbarea la fiecare parcurgere a perechilor de elemente consecutive care nu se afla in ordinea dorita. Astfel, dupa prima parcurgere elementul maxim al vectorului se va afla pe ultima pozitie, dupa a doua parcurgere, cele mai mari doua elemente se vor afla, in ordinea corespunzatoare, pe ultimele doua pozitii samd. Dupa cel mult n-1 parcurgeri, vectorul va fi sortat.

Denumirea metodei este sugestiva: elementele cu chei mari se ridica la suprafata, precum bulele in apa, plasandu-se in pozitiile lor finale.

Mecanismul de functionare este urmatorul: sa consideram vectorul A[]=.

Prima parcurgere:

[5 este elementul curent si are loc interschimbarea lui 9 cu 5]

[10 este elementul curent si nu are loc nici o interschimbare]

pozitie finala

Urmatoarele parcurgeri vor produce configuratiile:

pozitie finala

pozitie finala

1 2 4 3 5 6 7 8 9 10

O reprezentare pe verticala, de jos in sus a starii curente a masivului, ar fi poate mai sugestiva.

Se observa ca in exemplul considerat au fost suficiente 6 parcurgeri ale vectorului.

Sortarea prin metoda bulelor

#include<iostream.h>

void BubbleSort(int A[], int n)

}

main()

int n=sizeof(A)/sizeof(*A);

BubbleSort(A,n);

for(int i=0;i<n;i++) cout<<A[i];

return 0;

Observatie: a. Pentru a vizualiza modificarile ce au avut loc in vector dupa fiecare iteratie, se va include o secventa de afisare a vectorului in instructiunea for exterioara (dupa i).

b. Daca la o parcurgere nu a fost efectuata nici o interschimbare, atunci vectorul este in stare finala, sortat. Prin urmare, algoritmul a fost optimizat prin utilizarea suplimentara a variabilei booleene b.

Daca vectorul este deja sortat, se vor efectua n-1 comparatii -este parcurs o singura data-, daca vectorul este sortat in ordine inversa (cazul cel mai defavorabil) se efectueaza: la prima parcurgere n-1 comparatii, la a doua n-2 comparatii la ultima parcurgere avem de efectuat o singura comparatie. In total, sunt n*(n-1)/2 comparatii. In concluzie, metoda bulelor are timpul maxim polinomial: O(n²).

I.3.3.2   Sortarea rapida (Quick Sort)

Metoda consta in aplicarea succesiva a urmatorului procedeu: se alege un element oarecare al vectorului (numit prag sau pivot, de exemplu primul element sau cel din mijloc) si se permuta apoi, daca este cazul, celelalte elemente ale masivului astfel incat valorile mai mici decat pragul sa se afle in stanga pragului, iar cele mai mari in dreapta. Se obtin astfel doi sub-vectori, pentru care se repeta procedeul.

Asa cum se observa imediat, Quick Sort are la baza tehnica de programare Divide et Impera: vectorul initial a fost impartit in trei: partea nesortata din stanga pragului ce contine toate elementele mai mici decat acesta, o parte centrala din care face parte numai pragul, care ocupa pozitie finala si partea nesortata din dreapta pragului cu toate elementele mai mari decat acesta. In continuare, procedeul se va repeta pentru cei doi sub-vectori de dimensiuni variabile, din stanga, respectiv dreapta pragului, care au proprietatea ca toate elementele primului sub-vector sunt mai mici decat oricare element din cel de-al doilea.

In continuare, vom prezenta metoda de rezolvare imaginata de C.A.R. Hoare. Atunci cand a publicat-o, Hoare a insotit-o de una dintre cele mai detaliate prezentari publicate vreodata pentru o metoda de sortare. Hoare a denumit-o "metoda rapida de sortare" datorita performantelor sale remarcabile, pe care le vom analiza mai jos.

Sintetizand, mecanismul de partitionare este: fie i si j pozitiile a doua elemente ale masivului, initial i este 0 (prima pozitie in masiv), iar j este n-1 (ultima pozitie in masiv). Parcurgand vectorul, cu i de la stanga spre dreapta si cu j de la dreapta spre stanga, daca la un moment dat stim ca elementul A_i (comparand A_i cu pragul) trebuie sa se afle in sub-vectorul stang (A_i≤PRAG), trecem cu i mai departe la pozitia urmatoare, pana cand gasim un A_i mai mare decat pragul, care trebuie sa se afle in dreapta. Similar procedam cu j, micsorandu-l cu o unitate pana cand gasim un A_j mai mic decat pragul, ce trebuie sa fie in sub-vectorul stang. Daca i<j, atunci interschimbam A_i si A_j si trecem mai departe cu i si j, repetand procedeul de "ardere a lumanarii la ambele capete", pana cand i≥j. Odata ce i a depasit j, vom plasa pragul pe pozitia lui finala j, apoi vom repeta procedeul pentru cele doua jumatati de vector.

Algoritmul este urmatorul:

Trebuie subliniat faptul ca alegerea cheii este suficient de importanta. In cele ce urmeaza cheia va fi primul element al masivului. Acesta nu este neaparat cel mai mic element din vector, pentru simplul fapt ca este primul, asa cum poate am fi tentati sa credem!

Pentru exemplificare, sa consideram tabloul A[]= si sa urmarim valorile parametrilor considerati. Vom reprezenta pragul intr-un chenar, pozitia lui i este subliniata odata, iar pozitia lui j este subliniata de doua ori.

pragul va fi primul element al vectorului: PRAG=7. i va fi pozitia primului element (din stanga) mai mare decat PRAG=7, adica i=1 (am considerat ca vectorul este indexat incepand cu 0). Avem A[i]=9>PRAG=7.

j va fi pozitia celui mai din dreapta element mai mic sau egal cu PRAG=7, adica j=9. Avem A[j]=6<=PRAG=7.

Intrucat i<j, interschimbam elementele A[i] si A[j]. Rezulta noua configuratie:

Continuam deplasarea lui i si j: i devine 6, A[6]=10>PRAG=7, iar j devine 8, A[8]=3<=PRAG=7.

Intrucat i<j, interschimbam elementele A[i] si A[j]. Rezulta noua configuratie:

Continuand, i devine 7, A[7]=8>PRAG=7, iar j devine 5, A[6]=3<=PRAG=7. Pentru ca i il depaseste pe j, purcedem la plasarea pragului A[0] pe pozitia lui finala j. Vom avea:

Apoi repetam procedeul pentru cele doua jumatati de vector obtinute: (A[0], A[1] A[j-1]), respectiv (A[j+1] A[n-1]), ambele avand cel putin doua elemente.

Avem urmatoarea partitionare: prima parte: 3 6 5 4 2 1 si a doua parte: 8 10 9.

Se observa ca cele doua jumatati au proprietatea ca toate elementele din prima parte sunt mai mici decat pragul, care la randul sau este mai mic decat oricare element din partea a doua.

Intr-o noua iterare a algoritmului pentru prima jumatate, vom considera pragul 3 si in urma interschimbarii elementelor se va ajunge la doua sub-partitii: 2 1 , respectiv 4 5 6.

Algoritmul se repeta pentru toate subsirurile cu peste doua elemente, subsirurile obtinute fiind reprezentate schematic (sagetile indica reiterarile algoritmului, iar pragurile utilizate au fost hasurate):

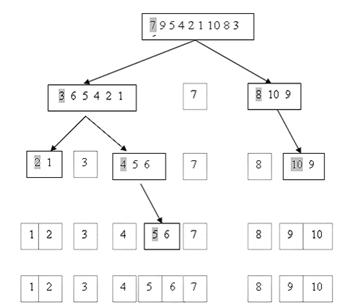
Fig. IV . Pozitionarea pragului si descompunerea in sub-probleme

Implementarea algoritmului in limbajul C/C++ este:

Sortarea rapida

#include<iostream.h>

void QuickSort(int A[], int p, int u)

}//while (i<j);

//plasam pragul A[p] pe pozitia sa finala j

//interschimbam pragul prag=A[p] cu A[j], daca e cazul

if(p!=j)

// daca este cazul repetam pentru vectorul din stanga (daca are cel putin doua elemente)

if(p<j-1) QuickSort(A, p, j-1);

// daca este cazul repetam pentru vectorul din dreapta (daca are cel putin doua elemente)

if(j+1<u) QuickSort(A, j+1, u);

main()

int A[]=;

int n=sizeof(A)/sizeof(A[0]);

QuickSort(A,0,n-1);

for(int i=0;i<n;i++) cout<<A[i];

return 0;

Indicatie: Pentru a vizualiza mai bine modul in care sunt impartiti vectorii, este indicat a se introduce dupa initializarea pragului o linie de afisare de forma:

cout<<endl<<prag<<':'; for(int k=p;k<=u;k++) cout<<' '<<A[k];

Avantajele metodei sunt esentiale: toate comparatiile, in cadrul unei parcurgeri se fac cu un singur prag, acesta va fi memorat, pentru un acces mai rapid, in registrii calculatorului. De asemenea numarul perechilor ce vor fi interschimbate, la o parcurgere, este limitat, deci efortul de deplasare a datelor este rezonabil.

Din nefericire rezultate absolut ineficiente se obtin atunci cand masivul este deja ordonat (crescator sau descrescator), caz in care fiecare partitionare se reduce la un subsir cu un singur element, fiind astfel inutila. In acest caz timpul de calcul este O(n²).

Valoarea pragului influenteaza in mod direct performantele metodei. Performante maxime sunt atinse atunci cand jumatatile pentru care se reia algoritmul sunt de lungimi aproximativ egale, lucru posibil daca am considera ca prag o valoare de mijloc (mediana) a vectorului. In acest caz, daca am nota T(n) numarul de comparatii efectuate, am avea ca:

unde (n-1) corespunde numarului de comparatii necesare pentru a imparti vectorul de dimensiune n in doua jumatati (se parcurg toate elementele cu doi indici, concomitent de la stanga catre dreapta, respectiv de la dreapta catre stanga, pana cand cei doi indici se intalnesc, in total n-1 elemente parcurse).

Se poate demonstra prin inductie matematica faptul ca formula recursiva de mai sus duce la: T(n)=nlog₂n.

I.3.4         Sortarea prin interclasare (Merge Sort)

Sortarea prin interclasare este si ea un exemplu de aplicare al metodei Divide et Impera si are la baza o idee foarte simpla: un vector poate fi sortat impartindu-l in doua jumatati, sortand separat cele doua jumatati si apoi interclasand secventele obtinute. Impartirea succesiva a unei secvente se face pana cand se ajunge la un vector cu un singur element, sau cu cel mult doua, caz in care daca elementele nu sunt in ordinea dorita, atunci ele se interschimba.

Fie, spre exemplu, vectorul A[]=.

Impartirea succesiva a sa in jumatati, urmata de interclasarea jumatatilor a fost reprezentata schematic mai jos:

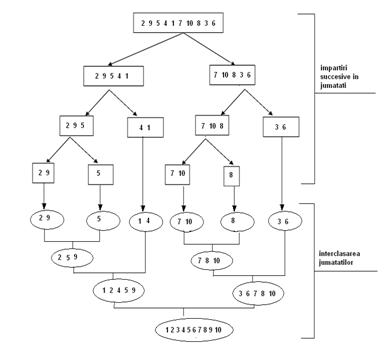
Fig. IV . Sortarea prin interclasare

Implementarea algoritmului in limbajul C/C++ este:

Sortarea prin interclasare

#include<iostream.h>

void Interclasare(int A[], int p, int m, int u)

void InterSort(int A[], int p, int u)

}

else //peste doua elemente

main()

int A[]=;

int n=sizeof(A)/sizeof(*A);

InterSort(A,0,n-1);

for(int i=0;i<n;i++) cout<<A[i];

return 0;

In ceea ce priveste numarul de comparatii, fie acesta T(n) pentru un masiv de dimensiune n. Putem presupune ca n este o putere a lui 2 (eventual in urma majorarii acestuia): . Sortarea masivului de dimensiune n a fost redusa la sortarea a 2 sub-vectori de dimensiuni egale n/2, iar interclasarea acestora necesita, asa cum am vazut intr-o sectiune anterioara, n/2+n/2=n comparatii. Rezulta ca:

Avem ca:

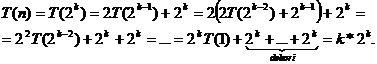
Cum , rezulta ca: , asadar algoritmul Merge Sort are ordinul O(nlog₂n).

I.3.5         Sortarea prin numarare

Desi are performante relativ scazute, metoda prezinta interes datorita faptului ca nu implica mutarea (interschimbarea) elementelor masivului. Ideea este de a numara pentru fiecare element al masivului cate elemente sunt mai mici decat el.

Sa consideram vectorul A[]=. Se va utiliza un vctor suplimentar B in care componenta B[i] reprezinta numarul de elemente mai mici decat A[i]. Fiecare element A[i] se compara pe rand cu cele din dreapta sa, A[j], j>i si se incrementeaza valoarea B[i] sau B[j] corespunzatoare elementului mai mare.

Elementele vectorului suplimentar B pot fi folosite ca indici intr-un alt vector ce contine elementele lui A in ordine crescatoare.

Implementarea algoritmului in limbajul C/C++ este:

Sortarea prin numarare

#include<iostream.h>

void NumSort(int A[], int n, int B[])

main()

,*B,*C;

int n=sizeof(A)/sizeof(*A);

B=new int[n];C=new int[n];

for(int i=0;i<n;i++) B[i]=0;

NumSort(A,n,B);

for(i=0;i<n;i++)

C[B[i]]=A[i];

for(i=0;i<n;i++)

cout<<C[i];

delete[]B;delete[]C;

return 0;

Algoritmul utilizeaza doi vectori suplimentari de dimensiune n, iar numarul de comparatii este n(n-1)/2, ceea ce face ca algoritmul sa aiba ordinul O(n²).

I.4          Sortare prin distribuire (chei multiple)

Sortarea prin distribuire este o metoda ce nu necesita nici o comparatie intre cheile elementelor, ea se bazeaza pe cifrele cheilor, avand ca efect sortarea alfanumerica, dupa cheie, a colectiei de date.

Mecanismul de functionare este asemanator modului in care poate fi aranjat un pachet de carti de joc daca dorim ca in final culorile sa se succeada astfel: trefla, romb, cupa, pica, iar cartile cu aceeasi culoare sa fie asezate in ordine crescatoare a numerelor. Se imparte pachetul in patru teancuri, dupa culoare, apoi se strang teancurile la un loc asezand treflele mai intai, peste ele romburile, apoi cupele si ultimele, picile. Apoi se imparte teancul din nou, de aceasta data dupa numere, obtinand 14 tenculete (As-10, J, Q, K), care, reunite, vor compune pachetul de carti in ordinea ceruta.

Explicatia este naturala: daca doua carti ajung, dupa ultima distribuire, in acelasi teanc, ele au acelasi numar, iar culorile lor sunt deja in ordinea corespunzatoare de la prima impachetare. Daca nu sunt in acelasi teanc, atunci nu au acelasi numar, iar cea cu numar mai mic se afla sub cea mai mare.

Exemplul pachetului de carti ne arata ca metoda sortarii prin distribuire se poate aplica (generaliza) pe orice multimi ordonate de forma

M₁ X M₂ X .X M_m,

unde fiecare M_k, k=1..m este total ordonata, dupa o anumita relatie de ordine, si are m_k elemente. In acest caz, pentru distribuirea elementelor dupa cifra k vor fi necesare m_k liste. Altfel spus, sortarea prin distribuire poate fi privita ca o sortare dupa mai multe chei.

Asadar, metoda are la baza tehnica Divide et Impera: se considera, succesiv, cifrele de pe aceeasi pozitie (mai intai cifra unitatilor, apoi cifra zecilor, sutelor samd.) si de fiecare data, se distribuie corespunzator elementele colectiei in 10 liste, apoi cele 10 liste sunt reunite (concatenate) si se reia procedeul pentru cifrele de pe pozitiile urmatoare.

Trebuie subliniat ca nu este obligatoriu ca elementele sa aiba acelasi numar de cifre, ele pot fi completate cu 0-uri la stanga pana se atinge dimensiunea maxima, fie m aceasta.

Ideea care a dus la imaginarea acestei metode considera cifrele incepand cu cea mai semnificativa, aseza numerele in 10 liste, iar pentru fiecare lista relua procedeul de impartire in alte 10 liste, de aceasta data dupa cea de-a doua cifra samd. Evident, rezultatul era sortarea masivului, insa erau utilizate 10^m liste. Pentru a inlatura acest inconvenient, cifrele au fost considerate in ordine inversa, incepand cu cea mai putin semnificativa, a unitatilor, apoi a zecilor samd., iar fiecare distribuire in liste era urmata de o concatenare a acestora, permitandu-se astfel reutilizarea lor la urmatoarea iteratie.

Ne propunem sa demonstram, prin inductie matematica, faptul ca dupa cea de-a k-a reuniune a listelor, numerele vor fi sortate alfanumeric dupa ultimele k cifre. Evident, daca aplicam rezultatul pentru k=n, obtinem ca datele sunt sortate.

Pentru k=1 rezultatul este evident din modul in care s-a realizat distribuirea in liste si reasamblarea lor. Sa presupunem rezultatul adevarat pentru k≥1 si sa-l demonstram pentru k+1. Daca a=a₁a₂.a_m si b= b₁b₂.b_m sunt doua numere aflate in aceasta ordine in lista reunita, atunci intre cifrele celor doua numere, aflate pe cea de-a k-a pozitie din dreapta pot exista relatiile:

a_m-k≠ b_m-k, in acest caz a si b vor fi repartizate in liste diferite; in urma reasamblarii va aparea mai intai in lista reunita numarul a, daca a_m-k<b_m-k, respectiv numarul b, daca b_m-k<a_m-k

a_m-k= b_m-k,, in acest caz a si b vor aparea in aceeasi lista, dar a il va preceda pe b, pentru ca sunt tratate in ordinea in care apar (conform ipotezei de inductie avem a_m-k.a_m,≤b_m-k.b_m) prin urmare si in lista finala a il va precede pe b.

Algoritmul metodei este:

Sa consideram, spre exemplu, masivul A[]=. Dupa distribuirea dupa cifra unitatilor, avem cele 10 liste:

Tabel IV . Distribuirea in cele 10 cozi dupa cifra unitatilor

Se concateneaza cele 10 liste si obtinem: 020, 311, 231, 221, 223, 586, 268, 368, 009.

O noua distribuire, dupa cifra zecilor de aceasta data, va genera listele:

Tabel IV Distribuirea in cele 10 cozi dupa cifra zecilor

Concatenam: 009, 311, 020, 221, 223, 231, 268, 368, 586.

Distribuind, din nou, dupa cifra sutelor, vom avea:

Tabel IV . Distribuirea in cele 10 cozi dupa cifra sutelor

Ultima concatenare genereaza sirul sortat: 009, 020, 221, 223, 231, 268, 311, 368, 586.

O observatie importanta care trebuie facuta este aceea ca dupa fiecare a k-a regrupare se obtine sirul sortat alfanumeric dupa ultimele k cifre.

Pentru rezolvare se vor considera doi vectori pentru capul/sfarsitul a 10 liste (cozi), adaugarea unui numar se face la sfarsitul fiecarei liste, iar extragerea, in vederea concatenarii, la capul ei. Pentru simplitate am considerat ca numerele au 3 cifre.

Implementarea algoritmului in limbajul C/C++ este:

Sortarea prin distribuire

#include<iostream.h>

#include<math.h>

struct TNod;

void Push(TNod* &cap, TNod* &sfarsit, int nr)

TNod* cap[10],*sfarsit[10];

void DistrSort(int *A, int n)

// se reunesc cele 10 cozi

int p=0;

for(i=0;i<10;i++)

while(cap[i])

//se afiseaza starea curenta a vectorului

cout<<endl<<'Ordonare alfanumerica dupa ultimele '<<k<<' cifre: ';

for(i=0;i<n;i++)cout<<A[i]<<' ';

}

main()

n=sizeof(A)/sizeof(*A);

DistrSort(A,n);

return 0;

I.5       Sortare topologica (ordonare partiala)

Sortarea topologica presupune ordonarea elementelor unei multimi pe care este definita o relatie partiala de ordine, adica intre oricare doua elemente ale multimii fie exista o relatie de ordine, fie sunt incomparabile. Vom spune despre masivul A=(a_i)_i=1..n ca este sortat topologic daca, oricare ar fi a_i <a_j vom avea i<j.

Acelasi lucru poate fi descris astfel: oricare doi indici consideram i<j, vom avea fie a_i <a_j, fie a_i si a_j sunt incomparabile.

De exemplu, sa presupunem ca dorim sa construim un mini-dictionar tehnic in care (unele) cuvinte sa fie definite cu ajutorul altor cuvinte, astfel ca nici un cuvant sa nu contina in definitia sa cuvinte care vor fi definite ulterior. Deci, orice cuvant va contine in definitia sa cuvinte care au fost deja definite sau care sunt de la sine intelese. Pentru aceasta problema, vom considera relatia de ordine:

daca a_i, a_j sunt doua elemente ale colectiei de date, spunem ca a_i <a_j ("a_i precede pe a_j") daca a_j contine in definitia sa pe a_i.

Evident, nu intre oricare doua elemente exista o ordine, asemenea perechi vor fi incomparabile.

O relatie partiala de ordine poate fi reprezentata grafic sub forma unui graf orientat, in care nodurile sunt elementele colectiei (sau mai simplu, indicii lor), iar arcele sunt date de: exista arc de la nodul i la nodul j daca a_i <a_j.

De exemplu, fie relatiile de ordine: 2<1, 4<2, 3<2, 4<3, 5<3. Graful de precedente va fi:

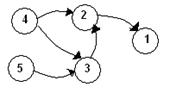
Fig. IV . Graf de precedente

O ordonare topologica pentru aceste date este: 4, 5, 3, 2, 1.

Trebuie observat faptul ca nu intotdeauna sortarea topologica are solutie. Daca in exemplul dictionarului exista o definitie circulara (graful de precedente contine un ciclu, de exemplu daca ar exista arcul 1<3), atunci o ordonare liniara a termenilor sai ar fi imposibila. De asemenea, daca exista, solutia nu este neaparat unica. Pentru exemplul considerat sunt posibile doua ordonari liniare, insa generarea uneia singure este suficienta:

sau 5, 4, 3, 2, 1.

Algoritmul de sortare topologica functioneaza dupa urmatorul principiu: initial se introduc in dictionar elementele care nu au predecesor (nu au definitii sau definitiile lor nu contin alti termeni ce trebuie definiti). Ulterior, se vor introduce in dictionar elemente ce contin in definitiile lor termeni care au fost deja definiti in dictionar (la pasii anteriori).

Pentru aceasta, va trebui sa cunoastem pentru fiecare element al colectiei (termen din dictionar, in exemplul nostru) numarul de predecesori si lista succesorilor. In acest sens vom considera vectorul pred de numere intregi si vectorul de capete de lista simplu inlantuita succ. Initial elementele lui pred sunt nule, iar listele sunt vide.

Pentru fiecare relatie de ordine de intrare, de forma p<s, se efectueaza urmatoarele doua actiuni:

numarul de predecesori ai lui s este incrementat;

in lista succesorilor lui p se introduce un nod nou s.

Odata ce toate relatiile de ordine au fost prelucrate, incepe sortarea: toate elementele cu valoarea 0 in pred sunt trimise la iesire si:

valoarea 0 din pred este inlocuita cu -1, cu semnificatia "prelucrat";

tuturor succesorilor (aflati in lista succesorilor) li se decrementeaza valoarea corespunzatoare din pred, intrucat un predecesor al lor a fost prelucrat.

Pentru exemplul de mai sus, pentru care avem relatiile: 2<1, 4<2, 3<2, 4<3, 5<3, mecanismul de functionare a metodei este urmatorul (elementele modificate la fiecare iteratie au fost redate cu caractere cursive):

starea initiala

Elementul Predecesori Lista succesori NULL NULL NULL NULL NULL

se citeste relatia: 2<1

Elementul Predecesori Lista succesori NULL NULL NULL NULL

se citeste relatia: 4<2

Elementul Predecesori Lista succesori NULL NULL NULL

se citeste relatia: 3<2

Elementul Predecesori Lista succesori NULL NULL

se citeste relatia: 4<3

Elementul Predecesori Lista succesori NULL NULL

se citeste relatia: 5<3

Elementul Predecesori Lista succesori NULL

In acest moment, se trece la ordonare si se preiau, pe rand (nu conteaza ordinea) elementele cu 0 predecesori: 4 si 5.

se prelucreaza 4

Elementul Predecesori Lista succesori NULL

se prelucreaza 5

Elementul Predecesori Lista succesori NULL

se prelucreaza 3

Elementul Predecesori Lista succesori NULL

se prelucreaza 2

Elementul Predecesori Lista succesori NULL

se prelucreaza 1

Elementul Predecesori Lista succesori NULL

Asadar, ordinea topologica generata este 4, 5, 3, 2, 1. Este utila observatia ca daca la o parcurgere nu se gaseste nici un element fara predecesori, atunci problema nu are solutie (avem o definire circulara).

Sortarea topologica

#include<iostream.h>

struct TNod;

TNod** succ;

int* pred;

void Inserare(TNod* &cap, int nr)

void Prelucreaza(int i)

void Parcurge(TNod* cap)

main()

for(i=0;i<n;i++)

// se tiparesc listele (pentru vizualizarea procesului)

for(i=0;i<N;i++)

Parcurge(succ[i]);

cout<<endl<<'Ordonare topologica: ';

int servite=0; bool no_sol;

do

if (no_sol)

}while(servite<N);

return 0;

Algoritmul de sortare topologica are timp maxim de executie de ordin O(n²), deoarece se efectueaza n parcurgeri si pentru fiecare element se parcurge lista de succesori, care poate avea cel mult n noduri.

Sortarea topologica isi gaseste aplicatii in multe domenii; ea este spre exemplu utilizata in probleme de planificare, cum ar fi ordonarea unor actiuni ce depind una de alta, in sensul ca o actiune nu poate incepe pana ce o alta nu s-a terminat; retele PERT samd.

I.6          Selectia

Selectia consta in determinarea celui al k-lea mai mic element al unui masiv. In continuare vor fi prezentate doua metode de selectie, metode derivate din doua metode de sortare: prin selectie directa, respectiv QuickSort.

I.6.1         Selectia directa

O solutie a acestei probleme deriva din metoda de sortare prin selectie directa si presupune o sortare partiala, numai a primelor k elemente ale masivului. Astfel, se determina minimul masivului si se interschimba cu primul element, apoi se determina minimul masivului, mai putin primul element, si se interschimba cu cel de-al doilea element. Se repeta procedeul de k ori. Evident, al k-lea cel mai mic element se va afla pe pozitia k in vectorul obtinut.

Daca din vectorul

dorim sa aflam cel de-al treilea element, atunci identificam minimul masivului (1) aflat pe pozitia 4 (am considerat elementele vectorului ca fiind indexate incepand cu valoarea 0), se interschimba primul element cu minimul, rezulta vectorul:

In continuare, ignorand primul element al vectorului, identificam un nou minim (3) aflat pe pozitia 7, pe care il interschimbam cu cel de-al doilea element al masivului. Avem:

In final (fiind cel de-al treilea pas), identificam minimul ignorand primele doua elemente pe pozitia 5 si il interschimbam cu cel de-al treilea element.

Asadar, al 3-lea cel mai mic element este 4.

Selectia directa

#include<iostream.h>

int Selectie(int A[], int n, int k)

return A[k-1];

main()

int n=sizeof(A)/sizeof(*A);

cout<<'Al 3-lea cel mai mic element este: '<<Selectie(A, n, 3);

return 0;

Algoritmul prezentat efectueaza n-1 comparatii la prima parcurgere, n-2 la cea de-a doua parcurgere, , n-k la parcurgerea k. In total, k*n-k*(k+1)/2 = k*n-k²/2-k/2. Cum valoarea maxima a lui k este n, rezulta ca, in cazul cel mai defavorabil (k maxim) algoritmul este polinomial de ordin O(n²).

Pentru ca variabila k poate lua orice valoare intre 1 si n, rezulta ca timpul mediu va fi 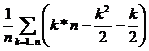. Cum si , obtinem ca timpul mediu este de ordin O(n²).

I.6.2         Selectia derivata din QuickSort

Un alt algoritm deriva din metoda de sortare rapida. Tinand cont ca procedura QuickSort utilizata pentru sortarea rapida are rolul de a aseza pragul (reamintim ca in implementarea de mai sus, primul element era considerat prag) pe pozitia lui finala in vectorul sortat, fie j aceasta, rezulta ca pragul este cel de-al j-lea element ca ordin de marime. Prin urmare, avem trei posibilitati:

daca j coincide cu k-ul cautat, atunci selectia se opreste, cel de-al k-lea mai mic element fiind chiar pagul;

daca j depaseste k, selectia celui de-al k-lea mai mic element se va repeta pe jumatatea stanga a vectorului, cea care contine elemente mai mici decat pragul;

daca j este mai mic decat k, selectia celui de-al k-lea mai mic element se va repeta pe jumatatea dreapta, cu elemente mai mari decat pragul.

Selectia derivata din QuickSort

#include<iostream.h>

int SelectQS(int A[], int p, int u, int k)

}//while (i<j);

//daca j este k incheiem

if(j==k) return prag;

//plasam pragul A[p] pe pozitia sa finala j

//interschimbam pragul prag=A[p] cu A[j], daca e cazul

if(p!=j)

// daca este cazul repetam pentru vectorul din stanga (are cel putin un element)

if(k<j && p<j) return SelectQS(A, p, j-1,k);

// daca este cazul repetam pentru vectorul din dreapta

if(j<u)return SelectQS(A, j+1, u,k);

main()

, e=4;

int n=sizeof(A)/sizeof(A[0]);

cout<<'Al '<<e<<'-lea cel mai mic element din vector este: '<<SelectQS(A,0,n-1,e-1);

return 0;

Spre deosebire de prima metoda, in algoritmul de mai sus numarul de comparatii nu mai este constant pentru un k oarecare, dar fixat. In cazul cel mai defavorabil, cand k=n si cand pentru fiecare reiterare j creste cu o unitate, numarul de comparatii va fi de ordin O(n²). Se poate demonstra insa faptul ca numarul mediu de comparatii de ordin O(n).