Arbori - Proprietati ale arborilor

1. Notiuni introductive

Exista mai multe moduri echivalente de definire a arborilor. Din punctul de vedere al teoriei grafurilor numim arbore un graf neorientat conex si fara cicluri. Daca graful este aciclic, dar nu este conex il vom numi padure.

De exemplu,

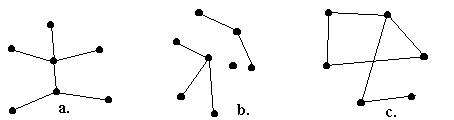
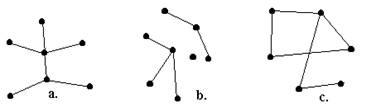
Fig. 1.

a. este arbore, b. este padure, nefiind conex, iar c. nu este nici arbore, nici padure, deoarece contine cicluri.

1.1. Proprietati ale arborilor

Teorema 1

Fie G (V, U) un graf neorientat. Urmatoarele afirmatii sunt echivalente:

1) G este arbore.

2) Oricare doua varfuri din G sunt unite printr-un lant simplu unic.

3) G este conex minimal (daca suprimam o muchie, graful obtinut este neconex).

4) G este conex si are V -1 muchii.

5) G este aciclic si are V -1 muchii.

6) G este aciclic maximal (daca adaugam o muchie, graful obtinut contine cicluri).

Demonstratie:

T

Daca G este arbore, atunci G este conex, deci oricare ar fi doua varfuri din graf, acestea sunt unite prin cel putin un lant simplu. Presupunem prin reducere la absurd ca exista x si y doua varfuri unite prin doua lanturi simple distincte l si l

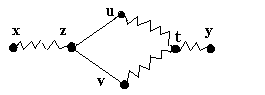
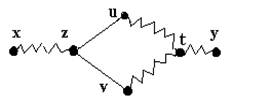
Fig. 2.

Fie z primul varf de la care cele doua lanturi se despart, iar t primul varf in care cele doua lanturi se intalnesc din nou. Daca notam l'₁ portiunea de pe lantul l₁ intre z si t, iar cu l'₂ portiunea de pe lantul l₂ intre z si t, atunci l'₁ si l'₂ nu au varfuri comune, cu exceptia varfurilor z si t. Concatenand l'₁ si l'₂, obtinem un ciclu- contradictie cu ipoteza ca G este arbore. Deci, oricare doua varfuri din graf sunt unite printr-un lant simplu unic.

2 T

Daca oricare doua varfuri x, yIV sunt unite printr-un lant simplu unic, atunci orice muchie x, y IU reprezinta unicul lant dintre x si y. Suprimand muchia x, y , intre x si y nu va mai exista lant, deci graful obtinut nu va mai fi conex.

3 T

Notam cu n numarul de varfuri si cu m numarul de muchii din graf.

Pentru a demonstra ca orice graf conex minimal are n-1 muchii vom demonstra prin inductie completa dupa n ca m n-1. Cum in orice graf conex m n-1, deducem m n-1.

P(1) Daca n 1, atunci m T m n-1.

P(2) Daca n 2, atunci m T m n-1.

P(n) Presupunem ca intr-un graf conex minimal cu cel mult n varfuri numarul de muchii este strict mai mic decat numarul de varfuri.

P(n Demonstram ca intr-un graf conex minimal cu n 1 varfuri, numarul de muchii este cel mult egal cu n.

Fie G conex minimal cu n 1 varfuri si m muchii. Eliminand o muchie oarecare din graf obtinem un graf G' cu m-1 muchii si doua componente conexe C₁ si C₂ cu n₁, respectiv n₂ varfuri (n₁ n₂ n 1) si m₁, respectiv m₂ muchii (m₁ m₂ m-1). Subgrafurile C₁ si C₂ sunt conexe minimale, altfel graful G nu ar fi conex minimal. Din ipoteza inductiva rezulta ca m₁ n₁-1, m₂ n₂-1; dar m₁ m₂ m-1 n₁ n₂ n-2 T m n-1. Deci G conex minimal implica G conex cu n-1 muchii.

T

Fie G un graf conex cu n-1 muchii. Sa demonstram ca G este aciclic.

Presupunem prin reducere la absurd, ca graful G contine un ciclu C format din varfurile v₁, v₂, , v_k.

Sa consideram subgraful partial G_k (V_k, U_k) constand din ciclul C. Deci V_k , iar U_k V_k U_k k). Daca V_k < V , atunci v_iIV_k si v_k IV-V_k astfel incat v_i, v_k IU, graful G fiind conex.

Construim G_k (V_k , U_k ) astfel :V_k V_k U_k U_k si U_k V_k k

Cat timp k 1 < n, aplicam acelasi procedeu pana cand obtinem un graf G_n (V, U_n), cu U_n n, U_n U; deci U n, contradictie cu ipoteza U n-1.

T

Presupunem ca graful G este aciclic cu n-1 muchii, sa demonstram ca G este aciclic maximal.

Fie C₁, C₂,, C_p cele p componentele conexe ale grafului G, avand respectiv n₁, n₂,, n_p varfuri si m₁, m₂,, m_p muchii fiecare. Evident ca n₁ n₂ n_p n si m₁ m₂ m_p n-1.

Cum graful G este aciclic, deducem ca fiecare componenta conexa este un arbore. Deoarece am demonstrat ca 1 T 5, rezulta ca m _i n_i-1, iI . Inlocuind in relatia de mai sus, obtinem n-p n-1 T p 1, deci G conex. Daca G este conex si aciclic, conform definitiei G este arbore. Dar am demonstrat ca 1 T 2, deci oricare doua varfuri din G sunt unite printr-un lant simplu. Astfel, adaugand orice muchie obtinem un ciclu.

T

Presupunem ca graful G este aciclic, dar daca am mai adauga o muchie s-ar obtine un ciclu. Sa demonstram ca G este conex.

Fie u si v doua varfuri neadiacente din graf, arbitrar alese. Deoarece adaugand muchia u, v se obtine un ciclu, rezulta ca u si v sunt unite printr-un lant ale carui muchii apartin grafului G. Cum u,v au fost alese arbitrar, deducem ca graful G este conex.

Q.E.D.

Teorema 2

Numerele intregi 0 < d d₂ d_n (n 2) sunt gradele varfurilor unui arbore daca si numai daca d₁ d₂ d_n 2n-2.

Demonstratie:

Necesitatea Conditia este necesara, deoarece orice arbore cu n varfuri are n-1 muchii, iar suma gradelor varfurilor oricarui graf este de doua ori numarul de muchii. Deci d₁ d₂ d_n 2n-2.

Suficienta Fie 0 < d d₂ d_n astfel incat d₁ d₂ d_n 2n-2.

Sa demonstram ca exista un arbore cu gradele varfurilor d₁, d₂,, d_n. Vom proceda prin inductie.

P(2)    Daca d₁ d₂ 2, atunci d₁ d₂ 1 , arborele fiind cel din figura de mai jos :

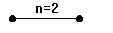
Fig. 3

P(n)    Presupunem acum ca proprietatea este adevarata pentru orice secventa de n numere naturale 0 < d d₂ d_n, astfel incat d₁ d₂ d_n 2n-2.

P(n Sa demonstram ca pentru orice secventa 0 < d'₁ d'₂ d'_n d'_n astfel incat d'₁ d'₂ d'_n 2n, exista un arbore cu n 1 varfuri cu secventa gradelor d'₁, d'₂, , d'_n

Observam ca exista macar un nod terminal x cu gradul d'₁ 1, altfel daca d_i iI T d'₁ d'₂ d'_n 2(n 1), ceea ce contrazice ipoteza. In mod analog, observam ca exista macar un nod neterminal x_n , cu gradul d'_n > 1, altfel daca d'_i iI T d'₁ d'₂ d'_n n 1 < 2n .

Sa consideram urmatoarea secventa de n numere intregi d'₂,, d'_n, d'_n -1 cu proprietatea ca d'₂ d'_n d'_n 2n-2. Din ipoteza inductiva exista un arbore A_n cu n varfuri si secventa gradelor d'₂,, d'_n, d'_n -1. Adaugam la arborele A_n un varf pe care il unim printr-o muchie cu varful avand gradul d'_n -1. Obtinem un arbore A_n cu gradele varfurilor d'₁, d'₂,, d'_n

Q.E.D.

Demonstratia acestei teoreme ofera si o solutie constructiva pentru obtinerea unui arbore cu secventa gradelor data.

Vom retine gradele varfurilor intr-un vector d de dimensiune n, ordonat crescator, cu suma componentelor egala cu 2n-2.

Arborele va fi reprezentat prin matricea muchiilor, o matrice a cu doua linii si n-1 coloane, in care pentru fiecare muchie din arbore vom retine extremitatile.

Spre deosebire de ideea din demonstratie, pentru a conserva ordinea in vectorul d, la fiecare pas al algoritmului gradul care va fi decrementat va fi primul grad mai mare ca 1 si nu ultimul.

Procedure Determinare Arbore;*

//vectorul d, matricea a si n, numarul de varfuri, sunt variabile globale

var NrMuchiiSelectate, VfTerminal, VfNeterminal: Integer;

begin

NrMuchiiSelectate :

VfTerminal :

while NrMuchiiSelectate < n-1 do

begin //selectez o muchie in arbore

VfNeterminal : VfTerminal

//caut un varf cu grad mai mare decat 1

while d VfNeterminal 1 do inc(VfNeterminal);

inc(NrMuchiiSelectate);

//selectez muchia VfTerminal,VfNeterminal

a 1,NrMuchiiSelectate VfTerminal;   

a 2,NrMuchiiSelectate VfNeterminal;

dec(d VfNeterminal

inc(VfTerminal);

end;

end;

De exemplu, pentru n 11 si sirul gradelor:

obtinem arborele din figura 4.

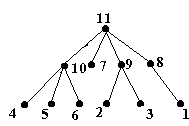
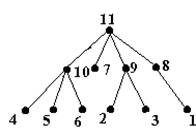
Fig. 4

Acest procedeu sugereaza o metoda foarte eficienta de reprezentare a arborilor. Daca A_n este un arbore cu varfurile x₁, x₂,.., x_n, suprimam varful terminal cu cel mai mic indice si muchia incidenta cu acesta si retinem a₁, varful adiacent cu varful terminal suprimat. Am obtinut astfel un subgraf cu n-2 muchii conex si aciclic, deci un arbore A_n-1. Repetam procedeul pentru arborele A_n-1, determinand un al doilea varf, a₂, adiacent cu varful terminal de indice minim ce va fi eliminat din A_n-1 impreuna cu muchia incidenta cu el s.a.m.d., pana cand se obtine un arbore A₂ cu doua varfuri adiacente.

Am obtinut astfel un sistem de n-2 numere 1 a_i n, iI asociat arborelui A_n numit codul Prffer al lui A_n.

Pentru arborele din figura 4, codul Prffer este a

Propozitie

Exista o corespondenta biunivoca intre multimea arborilor A cu n varfuri si multimea sistemelor , a_iI iI

Demonstratie:

Injectivitatea

Fie a a_i n, iI , codul Prffer al unui arbore A. Completam sirul cu a_n-1 n, deci a

Sa notam b (b₁, b₂, , b_n-2, b_n-1) indicii varfurilor in ordinea in care au fost eliminate. Observam ca :

1. b_i b_j, i j (deoarece un nod nu poate fi eliminat decat o data);

b_i a_i (pentru ca exista muchia a_i, b_i

b_i a_j, j > i (b_i fiind eliminat la pasul i, nu mai poate fi parintele unui alt varf eliminat ulterior);

4. k I , k este un varf terminal al arborelui A- , altfel k ar fi adiacent cu un varf ce va fi suprimat ulterior, deci k a_j, cu j > i- contradictie (un varf care nu a fost eliminat si care nu este parinte pentru un alt varf, este varf terminal).

5. b_i, din modul de definire a codului Prffer va fi :

b_i min k k

Deci din codul Prffer am putut determina in mod unic ordinea de eliminare a varfurilor si implicit, muchiile arborelui

A=

Surjectivitatea

Demonstram ca a a_i n, iI , exista un arbore A cu n varfuri astfel incat codul Prffer al lui A sa fie sirul a.

Completam a cu a_n-1 n si definim b_i conform relatiei (*), iI . Construim A, graful cu muchiile U a_i, b_i iI . Vom arata ca A este arbore si codul Prffer al lui A este

Notam U_i U- iI

V_i

Evident A A₁, iar A_n este format numai din varful n, deci A_n este arbore.

Sa demonstram ca b_i este varf terminal in A_i.

b_i min k k

Dar a_iIA_i, pentru ca din relatia (*) a_i b_j, j < i, iar b_i nu poate fi adiacent in A_i decat cu a_i, deoarece, daca b_i ar fi incident cu o alta muchie b_j, a_j , j > i din A_i ar insemna ca b_i b_j sau a_j b_i, cu j > i ceea ce este in contradictie cu definitia lui b_i.

A_i-1 se obtine din A_i eliminand varful terminal b_i si muchia b_i, a_i , incidenta cu aceasta. Procedand inductiv, cum A_n este arbore, deducem ca A_i, iI sunt arbori, in particular A este arbore.

Tot din definirea lui b_i rezulta ca b_i este varful terminal de indice minim, deci, conform definitiei, va fi codul Prffer al arborelui A_i. In particular deducem ca este codul Prffer al arborelui A.

Q.E.D.

Sa consideram, de exemplu, n 11 si a

Pentru a determina muchiile arborelui cu acest cod Prffer, completam codul cu a₁₀ 11. Deci a si determinam :

b₁ min

b₂ min

b₃ min

b₄ min

b₅ min

b₆ min

b₇ min

b₈ min

b₉ min

b₁₀ min

Muchiile arborelui sunt :

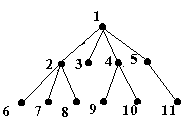
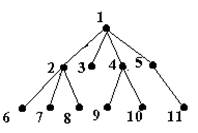
Fig. 5

Folosind acest rezultat, deducem ca numarul arborilor ce se pot construi cu n varfuri date este egal cu n^n-2, numarul functiilor bijective definite pe o multime cu n-2 elemente, cu valori intr-o multime cu n elemente. Aceasta formula poarta numele de formula lui Cayley.

Aplicatie*

Generati toti arborii cu n varfuri.

Problema se reduce la generarea tuturor functiilor

a:

si determinarea arborelui corespunzator fiecarei functii.

Vom genera toate codurile Prffer posibile recursiv, apeland procedura generare(1).

procedure generare(i:byte);

//pozitiile 1,2,,i-1 din vectorul global a sunt fixate;

// completam pozitiile i,,n-2.

begin

if i n-1 then // codul este complet

determina_arbore

else

for j : 1 to n do

begin

a i j;

generare(i

end;

end;

procedure determina_arbore;

// afiseaza muchiile arborelui;

var k, i: byte;

MB: set of byte;

//multimea varfurilor care au fost deja eliminate din arbore

MA: set of byte;

//multimea varfurilor pentru care trebuie sa determinam nodul

// terminal adiacent

begin

MB : ; MA : a₁, a₂, , a_n-1

for i : 1 to n - 1 do //determin cele n-1 muchii ale arborelui

begin

//calculez k, varful de indice minim ce MA MB

k :

while k in MA MB do inc(k);

MB : MB k

// k este nodul terminal de indice minim cautat

MA : MA - a_i

write(k, a_i,); //afisez muchia k,a_i

end;

end;

1.2. Arbori cu radacina

Pentru problemele in care se impune o ierarhizare a informatiilor ce corespund varfurilor arborelui, astfel incat anumite varfuri sa fie subordonate altora, este utila introducerea unei noi notiuni- arbore cu radacina. Arborii cu radacina sunt o prezenta cotidiana. Fiecare si-a reconstituit la un moment dat arborele genealogic si, dupa cum vom vedea, cea mai mare parte a termenilor folositi in limbajul informatic deriva de aici. Un alt exemplu este modul de organizare a competitiilor sportive sau organigrama unei intreprinderi. In multe alte exemple ii veti intalni pe parcursul acestei carti.

Definitie

Un arbore cu radacina este o multime finita de noduri care fie este vida fie

- exista un nod special numit radacina arborelui;

-toate celelalte noduri sunt partitionate in n 0 clase A₁, A₂, , A_n, fiecare clasa fiind un arbore cu radacina. Radacina arborelui este unita prin muchii de radacinile arborilorA₁, A₂, , A_n

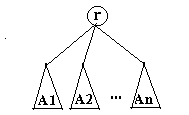
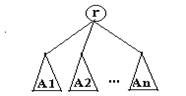
Fig.6.

Definitia este recursiva, orice nod al unui arbore fiind radacina unui subarbore.

Sa observam ca alegand intr-un mod arbitrar un varf drept radacina, orice graf neorientat conex si fara cicluri este un arbore cu radacina in sensul definitiei de mai sus. Arborii A₁, A₂, , A_n se numesc subarborii radacinii, numarul de subarbori nevizi ai unui nod fiind numit gradul nodului respectiv.

De exemplu,

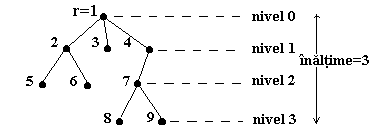
Fig. 7.   

Sa observam ca definitia conduce la o ierarhizare a nodurilor arborelui :

- consideram ca radacina r se situeaza pe nivelul 0.

- daca notam cu r₁, r₂, , r_n respectiv radacinile arborilor A₁, A₂, , A_n, nodurile r₁, r₂, , r_n vor constitui nivelul 1 in arbore, s.a.m.d.

Nodurile r₁, r₂, , r_n, se numesc fiii nodului radacina, iar radacina r reprezinta parintele nodurilor r₁, r₂, , r_n, radacina fiind singurul nod din arbore care nu are parinte. Fiecarei muchii din arbore ii putem asocia o orientare de la parinte spre fiu. In plus, fiii nodurilor de pe nivelul i 0, vor constitui nivelul i

Nivelul maxim din arbore va constitui inaltimea (adancimea) arborelui respectiv. Sa observam ca orice nod x poate fi atins din radacina pe un drum unic. Orice nod y care se gaseste pe drumul unic de la r la x se numeste ascendent (stramos) al lui x. Daca y este un ascendent al lui x, atunci x se numeste descendent al lui y. Mai exact, toti descendentii unui nod x sunt nodurile din subarborele cu radacina x. Daca un nod nu are descendenti el se numeste nod terminal sau frunza. Doua noduri care au acelasi parinte se numesc frati.

In exemplul de mai sus, 4 este un ascendent al lui 8. Nodurile 5, 6, 3, 8, 9 sunt noduri terminale. Nodurile 8, 9 sunt frati, iar descendentii nodului 4 sunt nodurile 7, 8, 9.

1.3. Arbori binari

O clasa foarte importanta de arbori cu radacina o constituie arborii binari. Un arbore binar este un arbore cu radacina in care gradul oricarui varf este cel mult egal cu doi. Putem defini recursiv arborii binari astfel :

Definitie

Un arbore binar este un arbore care fie este vid, fie consta dintr-un nod radacina si doi arbori binari disjuncti numiti subarborele stang, respectiv subarborele.

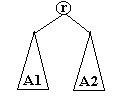
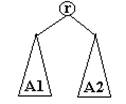
Fig. 8.

A₁ subarbore stang; A₂ subarbore drept.

Se face o distinctie clara intre subarborele drept si cel stang. Daca subarborele stang este nevid, radacina lui se numeste fiul stang al radacinii. Analog, daca subarborele drept este nevid, radacina lui se numeste fiul drept al radacinii.

De exemplu,

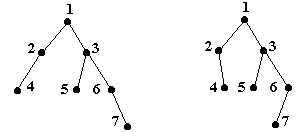
Fig. 9.

sunt doi arbori binari distincti.

In continuare, terminologia folosita la arbori cu radacina se va aplica si la arbori binari. Vom deosebi intre arborii binari cateva clase speciale:

1. Arbori binari stricti sunt arborii binari in care orice varf are gradul zero (este terminal ) sau doi (are exact doi fii).

De exemplu, arborii din figura 9 nu sunt arbori binari stricti (nodurile 2 si 6 avand un singur fiu), dar

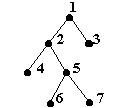
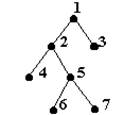
Fig. 10.

este un arbore binar strict.

2. Arbori binari plini sunt arbori binari care au 2^k-1 varfuri dispuse pe nivelurile 0, 1, , k-1, astfel incat pe fiecare nivel i se gasesc 2ⁱ varfuri.

De exemplu, arborele binar plin cu inaltimea 2 este:

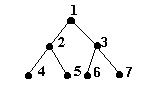
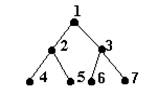
Fig. 11.

3. Arborii binari completi sunt arbori binari care se obtin dintr-un arbore binar plin prin eliminarea din dreapta catre stanga a unor noduri de pe ultimul nivel. Mai exact, pentru a construi un arbore binar complet cu n noduri, determinam k astfel incat

2^k n < 2^k k log₂n

Construim arborele binar plin cu 2^k -1 noduri si eliminam de pe ultimul nivel nodurile 2^k -1, 2^k -2, , n

De exemplu, arborele binar complet cu 5 varfuri se obtine prin eliminarea varfurilor 7 si 6 din arborele binar plin cu inaltimea 2 :

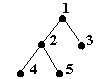
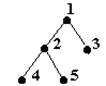
Fig. 12.

4. Arbori binari degenerati- sunt arbori binari cu n varfuri dispuse pe n niveluri.

De exemplu,

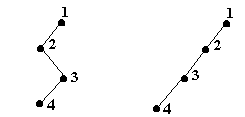
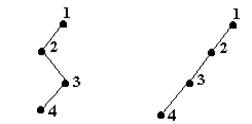
Fig. 13.

5. Arbori binari echilibrati - sunt arbori binari in care, pentru orice nod, numarul nodurilor din subarborele drept si numarul nodurilor din subarborele stang difera cu cel mult o unitate.

De exemplu,

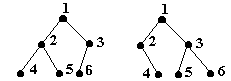
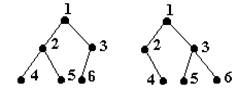
Fig. 14.

1.3.1 Proprietati ale arborilor binari

Proprietatea 1.

Numarul maxim de noduri de pe nivelul i al unui arbore binar este 2ⁱ.

Demonstratie:

Vom proceda prin inductie dupa numarul nivelului.

P(0)     Pe nivelul i 0 se gaseste un singur nod (radacina).

P(k)     Presupunem ca numarul maxim de noduri de pe nivelul k este

2^k.

P(k 1) Vom demonstra ca pe nivelul k 1 sunt cel mult 2^k noduri.

Pe nivelul k 1 se gasesc fiii nodurilor de pe nivelul k. Din ipoteza inductiva, pe nivelul k se gasesc cel mult 2^k noduri, iar fiecare nod poate avea cel mult doi fii, deci pe nivelul k 1 se gasesc cel mult 2 2^k 2^k noduri.

Q.E.D.

Proprietatea 2.

Numarul maxim de noduri intr-un arbore cu inaltimea h este 2^h

Demonstratie:

Numarul maxim de noduri intr-un arbore cu inaltimea h se obtine atunci cand fiecare nivel i este plin, deci, conform propozitiei anterioare, contine 2ⁱ noduri. Numarul maxim de noduri intr-un arbore cu inaltimea h va fi:

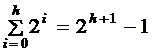
Q.E.D.

Proprietatea 3.

In orice arbore binar nevid cu n₀ noduri terminale exista n₀-1 noduri de grad 2.

Demonstratie

Notam cu n₀ numarul de noduri terminale, cu n₁ numarul de noduri de grad 1 si cu n₂ numarul de noduri de grad 2. Deci, numarul total de noduri n n₀ n₁ n_2.

Daca numaram muchiile dintr-un arbore binar, observam ca fiecare nod, cu exceptia radacinii, are o singura muchie orientata spre el. Notand m numarul de muchii obtinem n m 1. Dar orice muchie provine de la un nod de grad 1 sau 2, rezulta ca m n₁ 2n₂.

Din n₀ n₁ n₂ n si n₁ 2n₂ n-1 T n₂ n₀-1.

Q.E.D.

Proprietatea 4.

Un arbore cu n varfuri are inaltimea cel putin egala cu log₂n

Demonstratie:

In cazul cel mai favorabil, nodurile sunt dispuse pe niveluri astfel incat fiecare nivel sa fie plin, cu exceptia, eventuala, a ultimului nivel. Deci arborele binar cu n noduri de inaltime minima este arborele binar complet cu n varfuri, care, din modul de constructie, are inaltimea log₂n

Q.E.D.

Proprietatea 5.

Definim lungimea drumurilor interne (I) ca fiind suma lungimilor drumurilor de la radacina la noduri neterminale (interne) si lungimea drumurilor externe (E) ca fiind suma lungimilor drumurilor de la radacina la noduri terminale (frunza sau externe). Intr-un arbore binar cu n noduri interne, E I 2n.

Demonstratie:

Vom proceda prin inductie dupa n, numarul nodurilor interne.

P(0)     Intr-un arbore cu 0 noduri interne (vid sau format numai din radacina) E I

P(n-1) Presupunem ca intr-un arbore binar A_n-1, cu n-1 noduri interne, are loc relatia E_n-1 I_n-1 2(n-1).

P(n)     Vom demonstra ca intr-un arbore binar A_n, cu n noduri interne, are loc relatia E_n I_n 2n.

Fie A_n un arbore binar cu n noduri interne. Exista in A_n un nod intern x care are drept fii doua noduri terminale. Indepartand din A_n fiii nodului x, nodul x se transforma in nod terminal, deci obtinem un arbore A_n-1 cu n-1 noduri interne. Din propozitia inductiva rezulta ca in arborele A _n-1, E_n-1 I_n-1 2(n-1). Daca notam cu d, lungimea drumului de la radacina la nodurile eliminate, obtinem relatiile :

E_n E_n-1 2d-(d-1) (in A_n nodurile eliminate sunt terminale, dar nodul x nu, lungimea drumului de la radacina la x fiind d-1).

I_n I_n-1 (d-1) (in A_n nodul x este intern).

Deci E_n I_n-1 2(n-1) d I_n-d 2n-2 d I_n 2n.

Q.E.D.

1.4. Reprezentarea arborilor

1.4.1. Reprezentarea cu referinte descendente

Pentru fiecare nod din arbore vom retine informatia asociata nodului si referinte catre fiii sai. Daca presupunem ca gradul oricarui nod este cel mult egal cu n, putem reprezenta referintele spre fii printr-un vector cu n componente.

Structura unui nod va fi :

Declararea acestei structuri in sectiunea type in limbajul Pascal este :

Arbore ^NodArbore;

NodArbore record

Inf: TipInformatie;

Fiu: array 1..NrMaxFii of Arbore;

end;

Intr-o astfel de reprezentare risipa de memorie este foarte mare, in fiecare nod alocam memorie pentru numarul maxim de referinte catre fii. In plus, numarul maxim de fii este, in general, necunoscut. Acest neajuns ar putea fi eliminat folosind in locul vectorului de referinte (cu numar a priori fixat de componente) o lista simplu inlantuita in care sa retinem toti fiii nodului respectiv.

Declararea acestei structuri in sectiunea type in limbajul Pascal va fi :

ListaFii ^Fiu;

Fiu record

F: Arbore;

Urm: ListaFii;

end;

Arbore ^Nod Arbore;

NodArbore record

Inf: TipInformatie;

Ref: ListaFii;

end;

De exemplu, arborele din figura de mai jos,

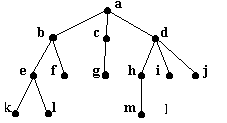
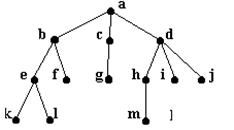
Fig. 15.

va fi reprezentat prin :

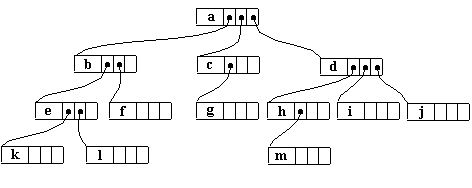
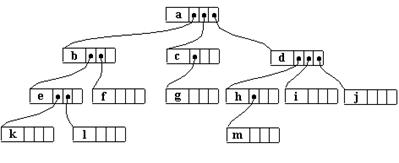
Fig.16.

Daca arborele este reprezentat prin referinte descendente, atunci este suficient sa retinem radacina arborelui pentru a avea acces la toate nodurile acestuia.

1.4.2. Reprezentarea cu referinte ascendente

In aceasta reprezentare, pentru fiecare nod din graf retinem pe langa informatia aferenta, o legatura spre nodul parinte.

Arbore ^NodArbore;

NodArbore record

Inf: TipInformatie;

Tata: Arbore;

end;

Mai simplu, putem utiliza doi vectori in care pentru fiecare nod retinem informatia, respectiv nodul parinte. Aceasta reprezentare este mai compacta, dar pentru a avea acces la toate nodurile arborelui trebuie sa retinem toate nodurile terminale.

De exemplu, pentru arborele din figura 15 vom obtine reprezentarea :

O astfel de reprezentare este utila pentru reprezentarea multimilor disjuncte cu ajutorul arborilor si o rezolvare eficienta a problemelor de reuniune a doua multimi si de determinare a multimii careia ii apartine un element dat.

1.4.3. Reprezentarea Fiu-Frate

Pentru fiecare nod retinem fiul cel mai din stanga si fratele lui din dreapta cel mai apropiat.

Arbore ^NodArbore;

NodArbore record

Inf: TipInformatie;

FiuSt, FrateDr: Arbore;

end;

Pentru arborele din figura 15 obtinem:

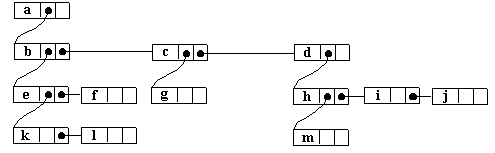
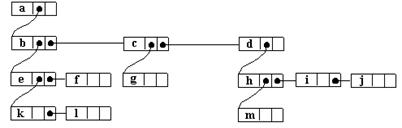
Fig. 17.

Rotind aceasta reprezentare cu 45 in sensul acelor de ceasornic, obtinem un arbore binar in care pentru fiecare nod, fiul drept este fratele lui din dreapta cel mai apropiat. Intre cele doua grafuri exista o corespondenta biunivoca. Figura de mai jos ilustreaza aceasta transformare.

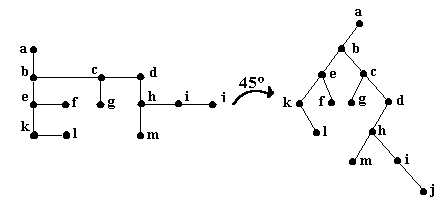
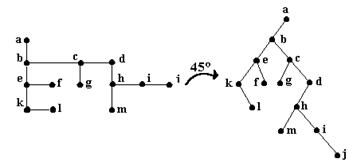
Fig. 18.

1.5. Reprezentarea arborilor binari

1.5.1. Reprezentarea inlantuita.

In aceasta reprezentare, pentru fiecare nod retinem, pe langa informatia asociata nodului, radacina subarborelui stang, radacina subarborelui drept si daca este necesar, parintele nodului respectiv.

ArboreBinar ^NodArboreBinar;

NodArboreBinar record

c: TipInformatie;

st, dr, parinte: ArboreBinar;

end;

Arborele binar va fi referit prin intermediul radacinii.

1.5.2. Reprezentarea secventiala.

Pentru fiecare nod retinem intr-un vector doar informatia asociata nodului, legaturile dintre noduri fiind implicite. Acest tip de reprezentare este convenabil pentru arbori binari completi. Pentru aceasta, vom numerota nodurile astfel :

- radacina este numerotata cu 1.

- cele 2ⁱ noduri de pe nivelul i sunt numerotate 2ⁱ, 2ⁱ 1, , 2ⁱ -1 de la stanga la dreapta(i > 0).

- pe ultimul nivel nodurile sunt numerotate pana la n, numarul de noduri din arbore.

Aceasta numerotare ne permite sa deducem legaturile existente intre nodurile arborelui.

Propozitie

Urmatoarele relatiii sunt valabile pentru orice nod x din arbore :

fiul stang al lui x este

fiul drept al lui x este

parintele lui x este

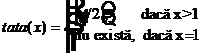
Demonstratie:

Vom demonstra relatiile 1. si 2. prin inductie dupa numarul nodului x, relatia 3. fiind o consecinta imediata a relatiiilor 1. si 2.

P(1)    Daca x 1, st(1) 2x, daca 2 n

dr(1) 2x 1, daca 3 n.

P(x) Presupunem ca relatiile 1. si 2. sunt indeplinite pentru nodul x.

P(x Demonstram relatiile 1. si 2. pentru x 1, adica

si

Fiul stang al nodului x 1 este precedat de fiul drept al nodului x. Din ipoteza inductiva, dr(x) 2x 1, deci st(x 2x 2x 2, evident, daca 2x n. Fiul drept al lui x 1 este succesorul lui st(x 1), deci dr(x 2x 2x 3, daca 2x n.

Q.E.D.

Deci pentru arbori binari completi aceasta reprezentare este ideala, nefiind necesara decat memorarea informatiilor nodurilor. Se poate utiliza reprezentarea secventiala si pentru arbori binari oarecare, completand arborele cu noduri fictive pana la un arbore binar complet, dar in acest caz o mare parte din vectorul ce contine informatiile nodurilor ramane neutilizata. In plus, ca orice reprezentare secventiala, este inadecvata pentru inserari si stergeri de noduri.

1.6. Operatii elementare pe arbori binari

In cele ce urmeaza, vom utiliza reprezentarea inlantuita a arborilor binari.

1.6.1. Crearea unui arbore binar.

Algoritmul de creare depinde in mod esential de tipul arborelui binar pe care dorim sa-l construim. Vom prezenta o procedura de creare a unui arbore binar echilibrat, alti algoritmi de creare fiind prezentati in capitolele urmatoare. Pentru a crea un arbore binar echilibrat cu n varfuri se stabileste un varf radacina, se construieste un arbore binar echilibrat cu n/2 varfuri ca subarbore stang si un arbore binar echilibrat cu n-1- n/2 varfuri ca subarbore drept. Daca n este par numarul nodurilor din subarborele stang va fi cu o unitate mai mare decat numarul nodurilor din subarborele drept, altfel cei doi subarbori au un numar egal de noduri.

function CreareArboreBinarEchilibrat(n: byte): ArboreBinar;

// functia intoarce adresa radacinii unui arbore binar echilibrat cu n //varfuri

var rad: ArboreBinar;

begin

if n 0 then //arborele este vid

CreareArboreBinarEchilibrat : nil

else

begin

new(rad) //aloc zona de memorie pentru radacina arborelui

readln(rad^.Inf);//citesc informatia radacinii arborelui

// creez subarborele stang, apoi cel drept

rad^. St : CreareArboreBinarEchilibrat(n div 2);

rad^. Dr : CreareArboreBinarEchilibrat(n - n div 2 -1 );

CreareArboreBinarEchilibrat : rad   

end

end;

1.6.2. Parcurgerea arborilor binari

Parcurgerile sunt cele mai frecvent utilizate operatii pe arbori. A parcurge un arbore inseamna a vizita fiecare nod al arborelui o singura data, in scopul prelucrarii informatiei asociate nodului.

Exista mai multe posibilitati de parcurgere a arborilor- in adancime (preordine, inordine, postordine) sau pe niveluri, dar in toate cazurile atat arborele, cat si subarborii sunt prelucrati in acelasi mod.

a) Parcurgerile in adancime

In toate cele trei tipuri de parcurgere in adancime se viziteaza mai intai subarborele stang, apoi subarborele drept. Diferenta consta in pozitia radacinii fata de cei doi subarbori. Fie scrise recursiv, fie iterativ, procedurile de parcurgere in adancime necesita o stiva.

Pentru a parcurge un arbore binar in preordine, se viziteaza mai intai radacina, se parcurge in preordine subarborele stang, apoi se parcurge in preordine subarborele drept.

procedure Preordine(rad: ArboreBinar);

begin

if rad nil then

begin

write(rad^.inf); //vizitez radacina

Preordine(rad^.st); //parcurg subarborele stang

Preordine(rad^.dr); //parcurg subarborele drept

end;

end;

Pentru a parcurge in inordine un arbore binar, se parcurge in inordine subarborele stang, se viziteaza radacina, apoi se parcurge in inordine subarborele drept.

procedure Inordine(rad: ArboreBinar);

begin

if rad nil then

begin

Inordine(rad^.st);

write(rad^.inf);

Inordine(rad^.dr);

end;

end;

Pentru a parcurge in postordine un arbore binar, se parcurge in postordine subarborele stang, apoi cel drept, apoi se viziteaza radacina.

procedure Postordine(rad: ArboreBinar);

begin

if rad nil then

begin

Postordine(rad^.st);

Postordine(rad^.dr);

write(rad^.inf);

end;

end;

Pentru a intelege mai bine operatia de parcurgere, vom prezenta si o varianta iterativa de parcurgere in inordine a unui arbore binar.

Pentru a simula recursia vom folosi o stiva S la care vom adauga sau sterge elemente in acelasi mod ca in procedura recursiva.

Stiva ^NodStiva;

NodStiva record

Inf: ArboreBinar;

Urm: Stiva;

end;

procedure InordineIterativ (rad: ArboreBinar);

// procedura parcurge iterativ in inordine arborele cu radacina rad

var S, p: Stiva;

NodCurent: ArboreBinar;

begin

S : nil;

NodCurent : rad;

repeat

while NodCurent nil do

begin

//adauga nodul curent in stiva S

new(p)

p^.Inf : NodCurent;

p^.Urm : S;

S : p;

//radacina subarborelui stang devine nod curent

NodCurent : NodCurent^.St

if S nil then //extrage un element din stiva

begin

p : S;

S : S^.Urm;

write(p^.inf)

NodCurent : p^.Inf^.Dr

dispose(p);

//elibereaza zona de memorie a lui p

until (S nil) and (NodCurent nil)

end;

Observatie

Fiecare nod din arbore este plasat si sters din stiva o singura data, deci timpul necesar parcurgerii inordine este de O(n). Spatiul suplimentar necesar depinde de inaltimea arborelui, deci in cazul cel mai defavorabil este de O(n).

b) Parcurgerea pe niveluri

Se viziteaza intai radacina, apoi fiul stang al radacinii, apoi cel drept si se continua in acest mod vizitand nodurile de pe fiecare nivel de la stanga la dreapta.

Pentru a realiza acest mod de parcurgere, vom utiliza o coada, pe care o initializam cu radacina arborelui si din care, la fiecare pas, vom extrage un nod, il vizitam si inseram in coada fii sai, daca acestia exista.

Coada ^NodCoada;

NodCoada record

Inf: ArboreBinar;

Urm: Coada;

end;

procedure ParcurgerePeNiveluri (rad: ArboreBinar)

//procedura parcurge pe niveluri arborele cu radacina rad

var C, SfC, p: Coada;

begin

if rad nil then //arborele este nevid

begin

new(C) // initializez coada cu radacina arborelui

C^.Inf : rad;

C^.Urm : nil;

SfC : C;

while C nil do // coada nu este vida

begin

p : C;

write(p^.Inf);

if p^.Inf^.St nil then begin

//adaug fiul stang in coada

new(q);

q^.Inf : p^.Inf^.St;

q^.Urm : nil;

SfC^.Urm : q;

SfC : q;

end;

if p^.Inf^.Dr nil then

begin //adaug fiul drept in coada

new(q);

q^.Inf : p^.Inf^.Dr;

q^.Urm : nil;

SfC^.Urm : q;

SfC : q;

end;

C : C^.Urm //extrag din coada nodul p

dispose(p);

end

end

end;

Observatie

Mai intai am inserat in coada fiii nodului ce urmeaza a fi vizitat si apoi am extras efectiv nodul respectiv din coada, pentru a evita inserarea unui nod intr-o coada vida.

1.6.3. Determinarea inaltimii unui arbore

Daca arborele este vid, vom considera ca inaltimea sa este -1, astfel putem calcula inaltimea arborelui ca fiind maximul dintre inaltimile subarborilor radacinii plus nivelul pe care se afla radacina.

function Inaltime (rad: ArboreBinar): integer;

// functia intoarce inaltimea arborelui binar cu radacina rad

begin

if rad nil then // arbore vid

Inaltime :

else

Inaltime : max(Inaltime(rad^.st), Inaltime(rad^.dr))

end

Am presupus cunoscuta functia max, care intoarce cel mai mare dintre cele doua argumente ale sale.

1.6.4. Egalitatea a doi arbori binari

Spunem ca doi arbori binari sint egali daca au aceeasi structura si contin aceleasi informatii in nodurile corespondente.

function Egali (rad1, rad2: ArboreBinar): boolean;

//functia intoarce true daca arborii cu radacinile rad1,

// respectiv rad2 sunt egali, altfel intoarce false

begin

Egali : (rad1 nil) and (rad2 nil) //ambii sunt vizi sau

or (rad1 nil) and (rad2 nil) // ambii sunt nevizi si

and (rad1^.c rad2^.c) //au aceeasi informatie in radacina

and Egali(rad1^.St, rad2^.St) //subarborii stangi egali

and Egali(rad1^.Dr, rad2^.Dr) // subarborii drepti egali

end;

Aplicatie*

Se dau secventele obtinute prin parcurgerile in preordine si in inordine ale unui arbore binar. Construiti arborele binar corespunzator.

De exemplu, fie A,B,C,D,E,F,G,H- parcurgerea in preordine si

C,B,A,E,D,G,F,H- parcurgerea in inordine.

Analizind parcurgerea in preordine, deducem ca nodul A este radacina. De asemeni, analizand parcurgerea in inordine, deducem ca nodurile C, B vor constitui arborele stang, iar D, E, G, F, H subarborele drept. Pentru a determina structura subarborelui stang, respectiv a subarborelui drept, procedam analog: din parcurgerea in preordine deducem ca B este radacina subarborelui stang, iar din parcurgerea in inordine deducem ca C este fiul stang al lui B. In mod similar, pentru subarborele drept deducem din parcurgerea in preordine ca D este radacina, iar din parcurgerea in inordine ca subarborele stang al lui D este format numai din nodul E, iar subarborele drept al lui D din nodurile F, G, H. Procedeul se repeta pina cind obtinem intreg arborele. Succesiunea operatiilor este ilustrata in figura 19:

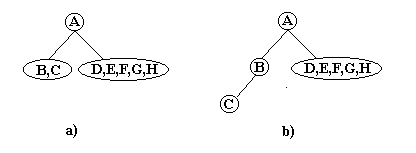
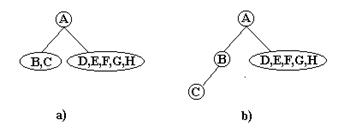
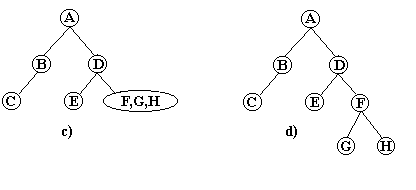
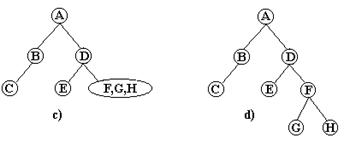
Fig. 19.

Propozitie

Succesiunile de noduri obtinute prin parcurgerile in inordine si in preordine ale unui arbore binar definesc in mod unic structura arborelui.

Demonstratie:

Vom proceda prin inductie completa dupa numarul de noduri.

P(1) Daca arborele are un singur nod, radacina, afirmatia este evidenta.

P(n) Presupunem ca pentru kI afirmatia este adevarata, adica pentru orice pereche de secvente inordine-preordine de lungime k, arborele binar corespunzator este unic.

P(n 1) Sa demonstram ca orice pereche de secvente preordine-inordine de lungime n 1 determina in mod unic un arbore binar.

Sa consideram o pereche de secvente preordine-inordine de lungime n 1. Primul nod din parcurgerea in preordine este in mod necesar radacina arborelui, celelalte n noduri fiind distribuite in subarbori: toate nodurile situate in stanga radacinii in parcurgerea in inordine vor constitui subarborele stang, nodurile situate in dreapta radacinii in parcurgerea inordine vor constitui subarborele drept.

Obtinem doua perechi de secvente preordine-inordine de lungime cel mult n, care din ipoteza inductiva, determina in mod unic subarborele stang, respectiv cel drept si in consecinta, cum radacina este in mod unic determinata, deducem ca perechea de secvente preordine-inordine de lungime n 1 determina in mod unic un arbore binar cu n noduri.

Q.E.D.

Vom descrie o functie recursiva ConstrArb, care determina arborele binar corespunzator unei perechi de secvente preordine-inordine date. Pentru simplificare, vom considera ca nodurile arborelui sunt numerotate in preordine de la 1 la n. Astfel, este suficient sa retinem intr-un vector global i indicii varfurilor in ordinea in care au fost atinse in inordine. Initial, apelam ConstrArb(1,1,n).

function ConstrArb (rad, st, dr): ArboreBinar;

//functia intoarce radacina arborelui unic determinat de parcurgerile //inordine-preordine

//rad este indicele radacinii arborelui

//st si dr sunt limitele intre care se gaseste parcurgerea inordine a //arborelui in vectorul i

var r: ArboreBinar;

IPozRad: byte;

begin

new(r); //aloc memorie pentru radacina arborelui

r^.c : rad; //retinem drept informatie numarul asociat nodului

IPozRad : st;

// determin pozitia radacinii arborelui in parcurgerea inordine

while i IPozRad rad do inc(IPozRad);

if IPozRad st then //subarborele stang este vid

r.st^ : nil

else

// i[ st.. IPozRad-1] contine subarborele stang

r.st^ : ConstrArb(rad 1, st, IPozRad-1);

if IPozRad dr then //subarborele drept este vid

r.dr^: nil

else

// i[ IPozRad 1.. dr] contine subarborele drept

r.dr^ : ConstrArb(rad IPozRad-st 1, IPozRad 1, dr);

// in subarborele stang au fost IPozRad-st 1 varfuri

end;

1.7. Numararea arborilor binari

Se pune problema determinarii numarului de arbori binari distincti cu n noduri, facand abstractie, bineinteles de numerotarea nodurilor.

Pentru n 0 sau n 1 exista un singur arbore binar.

Daca n 2, exista doi arbori binari distincti.

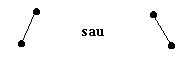
Fig. 20.

Pentru n 3, exista 5 astfel de arbori.

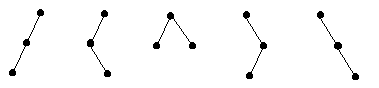
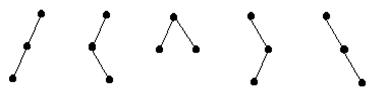
Fig. 21.

Notam cu b_n numarul arborilor binari distincti cu n noduri.

Evident, b₀

Pentru n > 0 arborii sunt formati din radacina si doi subarbori cu i, respectiv n-i-1 noduri (0 i < n).

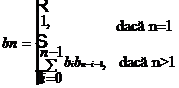
Pentru a obtine numarul arborilor binari distincti cu n noduri este suficient sa rezolvam aceasta relatie de recurenta. Sa consideram functia

Din relatia de recurenta, inmultind ambii membri cu xⁿ ,obtinem :

Sumand dupa n 1, obtinem :

Obtinem B(x)-b₀ x*B²(x) xB²(x) - B(x)

Rezolvand aceasta ecuatie de grad II obtinem :

Dezvoltand binomial (1-4x)^1/2 , obtinem:

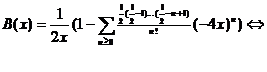
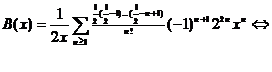
Notand n-1 cu m, obtinem:

Cum b_n este coeficientul lui xⁿ in B(x) obtinem

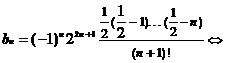
Numarul arborilor binari distincti cu n varfuri va fi aproximativ

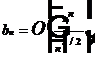
Observatii

1. Am demonstrat ca fiecarui arbore binar ii corespunde o singura pereche de secvente preordine-inordine. Considerand nodurile numerotate in preordine, rezulta ca arborii binari sunt definiti de permutarile inordine distincte (permutarile distincte ce se pot obtine trecand numerele 1,2,,n intr-o stiva si stergandu-le in toate modurile posibile).

Deci numarul permutarilor inordine de n elemente este

2. O problema care are in mod surprinzator legatura cu cele precedente este calculul produsului a n 1 matrici, M₀,M₁,,M_n. Cum inmultirea matricilor este asociativa, am dori sa stim in cate moduri putem calcula produsul M₀ M₁ M_n.

Pentru n 1 exista o singura posibilitate.

Pentru n 2 exista doua posibilitati: (M₀ M₁) M₂ sau M₀ (M₁ M₂).

Pentru n 3 exista cinci posibilitati :

((M₀ M₁) M₂) M₃;

(M₀ M₁) (M₂ M₃);

(M₀ (M₁ M₂)) M₃;

M₀ ((M₁ M₂) M₃ );

M₀ (M₁ (M₂ M₃)).

Notam cu P(n) numarul de moduri distincte in care putem calcula produsul M₀ M₁ M_n.

Produsul M₀ M₁ M_n poate fi impartit intr-un produs de doua produse de matrici : (M₀ M₁ M_k)(M_k M_n ).

Acestei asocieri i se poate pune in corespondenta un arbore binar:

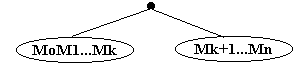
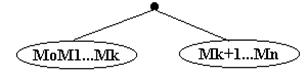
Fig. 22.

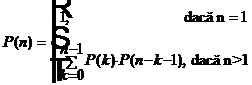
Deci numarul de parantezari posibile pentru produsul a n 1 matrici coincide cu numarul arborilor binari distincti cu n noduri.

1.8. Paduri

Definitie

O padure este un ansamblu de n 0 arbori disjuncti.

De exemplu,

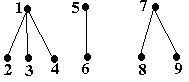
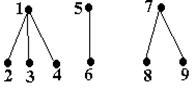
Fig. 23.

Indepartand radacina din orice arbore obtinem o padure formata din subarborii radacinii.

Orice padure poate fi reprezentata ca un arbore binar. Pentru aceasta, transformam arborii din care este constituita padurea in arbori binari, utilizand reprezentarea fiu-frate. Apoi construim arborele binar corespunzator padurii, utilizand campul frate al radacinii fiecarui arbore.

De exemplu, pentru padurea din figura 24 arborele binar asociat este

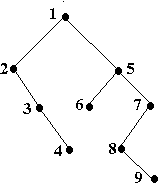
Fig. 24.

Definitie

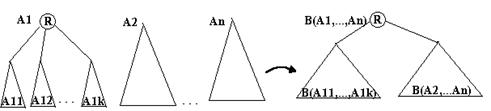
Fie A₁, A₂, , A_n arborii unei paduri. Atunci arborele binar corespunzator padurii, B(A₁, A₂, , A_n) este:

1.vid, daca n

2.are radacina egala cu radacina lui A₁, subarborele stang este arborele corespunzator padurii formata din subarborii lui A₁, iar subarborele drept este arborele binar corespunzator padurii formata din arborii A₂, , A_n.

Operatiile de parcurgere a unei paduri se reduc la parcurgerea arborelui corespunzator.

Fig. 25.

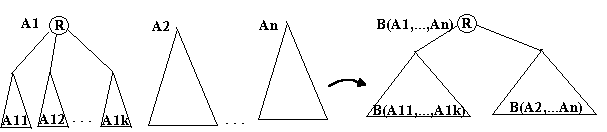
Probleme rezolvate

1.9.1. Arbori binari m-ponderati

-Olimpiada de informatica faza judeteana, Iasi 1995-

Un arbore binar strict se numeste m-ponderat daca fiecare nod i are asociata o pondere p i , cu valori intre 1 si m-1, astfel incat pentru orice nod terminal t suma ponderilor din nodurile aflate pe drumul de la radacina la nodul t este egala cu m.

Definim P_n,m(T) ponderea unui arbore binar strict cu n noduri terminale m-ponderat ca fiind suma ponderilor atasate nodurilor din T. Sa se scrie un program care pentru n si m dati determina un arbore binar strict m-ponderat cu n noduri terminale T* astfel incat:

P_n,m(T*) max

Solutie:

Pentru ca problema sa admita solutie trebuie ca pentru orice drum de la radacina la un nod terminal sa putem asocia nodurilor ponderi

Inaltimea minima a unui arbore cu n varfuri terminale este h log₂n . Pentru a asocia ponderi este necesar ca m, suma ponderilor varfurilor de pe orice drum de la radacina la un varf terminal, sa fie cel putin egala cu log₂n

Deci conditia necesara pentru ca problema sa admita solutie este m log₂n

Observatii

1. Fie T un arbore binar strict cu n varfuri terminale. Construim o m-ponderare p_o a arborelui T astfel:

-asociem fiecarui nod interior ponderea 1.

-deoarece suma ponderilor de pe orice drum de la radacina la un varf terminal trebuie sa fie egala cu m, asociem fiecarui nod terminal o pondere egala cu m-lungimea drumului de la radacina la nodul terminal respectiv.

Demonstram ca p_o este o m-ponderare maximala pentru arborele T.

Sa consideram p o m-ponderare oarecare pentru arborele T si x un varf interior astfel incat p x >1. Daca exista mai multe astfel de noduri, consideram un varf de pe un nivel de rang minim. Fie y si z cei doi fii ai lui x. Construim o alta m-ponderare p a lui T astfel:

p' x 1; p' y p y p x -1; p' z p z p x

Atunci P'(T) P(T)-p x -p y -p z p'[x] p' y p' z T

P'(T) = P(T) -p x -p y -p z 1+ p y p x p z p x T

P'(T) P(T) p x T P'(T) > P(T).

Modificand succesiv ponderile nodurilor interioare de sus in jos, obtinem dupa un numar finit de pasi m-ponderarea p_o, in care toate varfurile interioare au ponderea 1.

Deci P_o(T) P(T), p o m-ponderare a arborelui T

2. Observatia 1. ofera o modalitate de m-ponderare optimala a unui arbore binar strict dat. Ramane sa determinam, pentru n si m dati, arborele binar strict cu n varfuri terminale care maximizeaza P_n,m(T). Demonstram ca arborele cautat T* este arborele binar complet. Fie T un arbore binar strict cu n varfuri terminale care nu este complet si fie x si y doua varfuri terminale fii ai aceluiasi nod interior, situate pe nivelul i, iar z un nod terminal situat pe nivelul j, astfel incat i-j > 1.

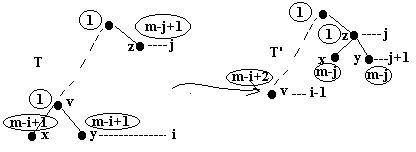
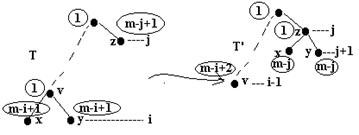
Fig. 26.

Mutam nodurile x si y de pe nivelul i pe nivelul j 1, ca fii ai nodului z si reponderam nodurile.

P(T') P(T)-2(m-i 1)-1-(m-j 2(m-j) m-i T

P(T') P(T) i-j-1 > P(T).

Aplicam succesiv aceasta transformare pana cand obtinem un arbore binar complet.

Deci P(T*) > P(T), T arbore binar strict.

Q.E.D.

Reprezentarea informatiilor

Arborele cautat fiind complet, pentru implementare alegem reprezentarea secventiala.

program arbore_m_ponderat;

uses crt;

const NMaxVfT=20;

NMaxVf=2*NMaxVfT-1;

type Vf=0..NMaxVf;

arbore_ponderat=array[Vf] of word;

var n,i,nivel:Vf;

m:word;

p:arbore_ponderat;

procedure afisare;

const pst=13;

pdr=28;

pp=42;

var i:Vf;

begin

writeln('Nodul Fiu stang Fiu drept Pondere');

for i:=1 to n-1 do

begin

write(i);

gotoxy(pst,wherey);write(2*i);

gotoxy(pdr,wherey);write(2*i+1);

gotoxy(pp,wherey);writeln(1);

end;

for i:=n to 2*n-1 do

begin

write(i);

gotoxy(pp,wherey);writeln(p[i]);

end

end;

begin

clrscr;

write('n=');readln(n);

write('m=');readln(m);

if m<trunc(ln(n)/ln(2))+1

then writeln('Nu exista solutie!')

else

begin

for i:=1 to n-1 do p[i]:=1;

for i:=n to 2*n-1 do

begin

nivel:=trunc(ln(i)/ln(2));

p[i]:=m-nivel;

end;

afisare

end;

readln

end.

1.9.2. Interclasarea optimala a n siruri ordonate

Fie n secvente S₁,S₂,,S_n de lungimi respectiv L₁,L₂,,L_n, ordonate nedescrescator. Sa se interclaseze cele n secvente.

Solutie

1. Notam cu m L₁ L₂ L_n.

O prima solutie ar fi sa selectam la fiecare pas articolul cu cheia cea mai mica si sa-l plasam in sirul rezultat. Pentru selectarea minimului ar fi necesare n-1 comparatii, deci algoritmul ar fi de O(n.m).

2. Vom utiliza un arbore de selectie.

Definitie

Numim arbore de selectie un arbore binar complet in care fiecare nod este cel mai mic dintre fiii sai.

Observatie

Fiecare nod din arbore are asociata ca valoare minimul valorilor nodurilor din subarborele corepunzator.

Vom construi arborele de selectie in mod bottom-up, apoi la fiecare pas selectam minimul, care este radacina arborelui si restructuram arborele.

Constructia arborelui de selectie este de O(n), restructurarea arborelui, care se repeta de m ori, de O(log n). Deci algoritmul va fi de O(m log n).

Reprezentarea informatiilor

Arborele de selectie fiind complet, vom utiliza reprezentarea secventiala.

program interclasare_optimala;

const NMaxSecv=20;

LgMaxSecv=50;

type Ind=1..LgMaxSecv;

Secv=1..NMaxSecv;

Nod=1..2*NMaxSecv;

Arbore=array[Nod] of integer;

var l:array[Secv] of Ind;

n:Secv;

m,k:word;

o:array[1..LgMaxSecv*NMaxSecv] of integer;

s:array[Secv,Ind] of integer;

A:Arbore;

j:array[Secv] of Ind;

procedure citire;

var f:text;

i:Secv;

j:Ind;

begin

assign(f,'int.in'); reset(f);

readln(f,n);

for i:=1 to n do read(f,l[i]);

readln(f);

for i:=1 to n do

begin

m:=m+l[i];

s[i,l[i]+1]:=MaxInt;

for j:=1 to l[i] do read(f,s[i,j]);

readln(f);

end;

close(f);

end;

procedure ConstrArbSel;

var i:Nod;

begin

for i:=n to 2*n-1 do A[i]:=s[i-n+1,1];

for i:=n-1 downto 1 do

if A[2*i]<A[2*i+1] then

A[i]:=A[2*i]

else

A[i]:=A[2*i+1];

for i:=1 to n do j[i]:=1;

end;

procedure restructurare;

var i,tata,frate:Nod;

begin

i:=1;

while i<=n-1 do

if A[i]=A[2*i] then

i:=2*i

else

i:=2*i+1;

inc(j[i-n+1]);

A[i]:=s[i-n+1,j[i-n+1]];

while i>1 do

begin

tata:=i div 2;

if i=2*tata then frate:=2*tata+1

else frate:=2*tata;

if A[i]>A[frate] then A[tata]:=A[frate]

else A[tata]:=A[i];

i:=tata;

end;

end;

procedure afisare;

var i:word;

begin

writeln('Rezultatul interclasarii: ');

for i:=1 to m do

write(o[i],' ');

writeln;

readln

end;

begin

citire;

ConstrArbSel;

for k:=1 to m do

begin

o[k]:=A[1];

restructurare;

end;

afisare;

end.

1.9.3. O reprezentare a arborilor binare stricti

-problema propusa de Horia Georgescu, G.I. nr.10/1993-

Fie urmatorul arbore binar strict

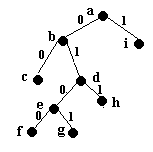
Fig. 27.

Codificam drumurile de la radacina la nodurile terminale marcand cu 0 fiecare deplasare la stanga si cu 1 fiecare deplasare la dreapta. Concatenand codificarile in preordine, obtinem o reprezentare a arborilor binari stricti.

Pentru exemplul din figura 27 codificarea este 00010001010111.

Problema

Data fiind s, reprezentarea unui arbore binar strict obtinuta prin concatenarea in preordine a codificarilor drumurilor de la radacina la nodurile terminale, generati arborele corespunzator.

Solutie

Fie x, y doua noduri terminale, situate pe nivelul maxim in arbore, fii ai aceluiasi nod t. Daca notam p secventa ce codifica drumul de la radacina la t, atunci sirul s are forma ap0p1b. Determinam p astfel incat s ap0p1b, p fiind cea mai lunga secventa cu aceasta proprietate. De exemplu, pentru codificarea de mai sus p

Putem construi astfel un drum de la radacina arborelui la doua noduri terminale frati.

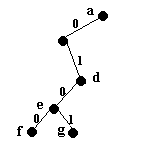
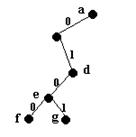
Fig. 28.

Eliminam din s secventa 0p1, ceea ce corespunde eliminarii din arbore a doua noduri terminale fii ai aceluiasi nod. Obtinem, de exemplu, s

Am redus problema la generarea unui arbore cu un nod terminal mai putin, pe care il vom suprapune peste drumul generat anterior.

program Generare_Arbore_Binar_Strict;

uses crt;

type Arbore=^NodArbore;

NodArbore= record

st,dr:Arbore

end;

var s:string;

f:text;

n, poz, NrNod, lg, NrTest: byte;

A, T: Arbore;

procedure procesare(var poz, lg: byte);

var i,j: byte;

begin

lg:=0; poz:=1;

i:=1;

while i<=n-2*lg-1 do

begin

j:=lg+1;

while i+2*j<n do

begin

while (i+2*j<n) and (s[i+j]<>'0') do inc(j);

if i+2*j<n then

if (copy(s,i,j)=copy(s,i+j+1,j)) and (s[i+2*j+1]='1')

then begin

lg:=j;

poz:=i

end;

inc(j);

end;

inc(i)

end;

end;

procedure ConstrDrum;

var q, x: Arbore;

gata: boolean;

i: byte;

begin

q:=A; i:=poz;

gata:=false;

while not gata and (i<poz+lg) do

if s[i]='0' then

if q^.st<>nil then

begin

q:=q^.st;

inc(i)

end

else gata:=true

else

if q^.dr<>nil then

begin

q:=q^.dr;

inc(i)

end

else gata:=true;

while i<poz+lg do

begin

new(x);

x^.st:=nil; x^.dr:=nil;

if s[i]='0' then

q^.st:=x

else

q^.dr:=x;

q:=x;

inc(i)

end;

new(x);

x^.st:=nil; x^.dr:=nil;

if q^.st=nil then q^.st:=x;

new(x);

x^.st:=nil; x^.dr:=nil;

if q^.dr=nil then q^.dr:=x;

end;

procedure scrie(x: Arbore; niv, st, dr: byte);

var poz: byte;

begin

if x<>nil then

begin

poz:=(st+dr)div 2;

gotoxy(poz,niv);

write(NrNod);inc(NrNod);

scrie(x^.st, niv+2, st, poz-1);

scrie(x^.dr, niv+2, poz+1, dr);

end;

end;

procedure afisare;

begin

clrscr;

inc(NrTest);

NrNod:=1;

writeln('Testul nr. ', NrTest,':');

scrie(A,2,1,80);

readln;

end;

begin

assign(f,'a.in');

reset(f);

while not seekeof(f) do

begin

readln(f,s);

new(A);

A^.st:=nil; A^.dr:=nil;

repeat

n:=length(s);

procesare(poz,lg);

ConstrDrum;

delete(s,poz+lg,lg+2);

until n=0;

afisare;

end;

readln

end.

Exercitii

Demonstrati ca in orice graf G (V, U) conex, U V

Demonstrati ca in orice arbore exista cel putin doua varfuri terminale.

3. Calculati numarul arborilor cu n varfuri si secventa gradelor varfurilor d₁,d₂,,d_n (d_i iI , d₁ d₂ d_n 2n-2). Scrieti un program de generare a tuturor arborilor cu secventa gradelor data.

4. Calculati numarul arborilor cu n varfuri, dintre care p terminale.

5. Secventele obtinute prin parcurgerile in postordine si in inordine ale unui arbore binar definesc in mod unic arborele? Daca da, scrieti un algoritm de generare a arborelui binar corespunzator.

Aceeasi problema pentru parcurgerile in preordine si in postordine, respectiv parcurgerea in inordine si parcurgerea pe niveluri.

6. Generati toti arborii binari distincti cu n varfuri.

7. Scrieti o functie de duplicare a unui arbore binar.

8. Scrieti o functie de cautare a unei valori de tipul informatiei asociate nodurilor intr-un arbore binar. Analizati complexitatea functiei.

9. Scrieti o procedura iterativa de parcurgere in preordine a unui arbore binar.

10. Scrieti o procedura iterativa de parcurgere in postordine a unui arbore binar.

11. Scrieti o functie de stergere a unui arbore binar.

12.Scrieti un program care sa parcurga un arbore oarecare in reprezentarea fiu-frate pe niveluri.

13. Definim gradul unui arbore cu radacina ca fiind gradul maxim al nodurilor sale. Fie un arbore cu gradul k si inaltimea h. Care este numarul maxim de noduri din acest arbore ?

Reprezentam fiecare nod al arborelui printr-un articol ce contine informatia asociata nodului si k pointeri spre radacinile subarborilor :

Arbore ^NodArbore;

NodArbore record

c: TipInf;

leg: array 1..k of Arbore;

end;

a). Scrieti o functie de creare a unui arbore echilibrat de grad k.

b). Descrieti algoritmul de parcurgere pe niveluri si in adancime a unui arbore de grad k.

c). Scrieti o functie care sa determine inaltimea unui arbore de grad k.

d). Scrieti o functie care sa testeze egalitatea a doi arbori de grad k.

14. Scrieti o functie care sa determine numarul de noduri terminale ale unui arbore binar.

15. Scrieti un algoritm care, dat fiind un arbore binar, schimba fiul stang cu fiul drept, pentru orice nod din arbore. De exemplu :

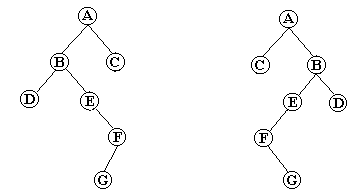
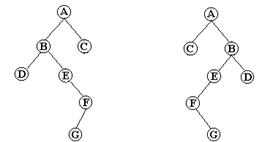
Fig. 29.

16. Demonstrati ca orice arbore binar este 2-colorabil.

17. Fie P un poligon convex. O diagonala este un segment ce uneste doua varfuri neadiacente. Numim triangularizare a poligonului convex P o multime de diagonale care impart poligonul in triunghiuri disjuncte.

Calculati numarul triangularizarilor posibile pentru un poligon convex cu n varfuri.

18. Scrieti o functie care sa verifice daca un arbore binar este strict.

19. Calculati numarul arborilor binari de inaltime h.

20. Scrieti un program care sa construiasca arborele binar corespunzator padurii formate din arborii A₁, A₂, , A_n si parcurgeti arborele in preordine, inordine, postordine.

21. Fie P o padure, arborii componenti fiind reprezentati prin referinte ascendente. Scrieti un algoritm care sa determine pentru oricare doua varfuri din padure cel mai apropiat ascendent comun, daca acesta exista. Analizati complexitatea algoritmului.

22. 'Problema' telefonistelor

O retea telefonica formata din n centrale numerotate de la 1 la n, are forma unui arbore oarecare. Telefonista de la centrala k, 1 k n, care a intrat in posesia unei informatii importante, arde de nerabdare s-o impartasesca tuturor colegelor ei. Stiind ca fiecare telefonista poate vorbi la un moment dat doar cu una dintre vecinele ei, ca o convorbire dureaza un minut si ca fiecare telefonista, dupa ce a intrat in posesia informatiei se grabeste sa o comunice celorlalte vecine ale ei care n-au aflat-o inca, sa se determine succesiunea propagarii in timp a informatiei si timpul minim necesar ca toate telefonistele sa cunoasca vestea pornita de la centrala k.

Anexa

program Constructie_arbore_cu_secventa_gradelor_data;

const NMaxVf = 20;

type Vf = 1..NMaxVf;

var a, d: array[Vf] of Vf;

n, i, VfT, VfNt: Vf;

s: byte;

fout: text;

procedure citire;

var i: Vf;

fin: text;

begin

assign(fin, 'grade.in'); reset(fin);

readln(fin, n);

for i := 1 to n do read(fin, d[i]);

readln(fin);

close(fin);

end;

procedure afisare;

var i: Vf;

begin

writeln(fout, 'Muchiile arborelui sunt: ');

for i := 1 to n-1 do write (fout, '(', i, ',', a[i], ') ');

writeln(fout);

end;

begin

citire;

assign(fout,'grade.out'); rewrite(fout);

s := 0;

for i := 1 to n do s := s+d[i];

if s <> 2*(n-1)then

writeln(fout,'Secventa eronata! Suma gradelor trebuie sa fie 2(n-1)!')

else

for VfT := 1 to n-1 do

begin

VfNt := VfT+1;

while (VfNt < n) and (d[VfNT] = 1) do inc(VfNt);

a[VfT] := VfNt;

dec(d[VfNT]);

end;

afisare;

close(fout);

end.

De exemplu, pentru fisierul de intrare:

fisierul de iesire va contine:

Muchiile arborelui sunt:

program Generare_Arbori_cu_n_Varfuri;

const NrMaxVf=10;

type Vf = 1..NrMaxVf;

Arbore = array[Vf] of Vf;

var n: Vf;

fout: text;

a: Arbore;

NrArb: longint;

procedure determina_arbore;

var MB, MA: set of Vf;

i, k: Vf;

begin

inc(NrArb);

write(fout, 'Arborele nr. ',NrArb,' :');

MB := []; MA := [];

for i := 1 to n-1 do MA := MA+[a[i]];

for i := 1 to n-1 do

begin

k := 1;

while k in MA+MB do inc(k);

MB := MB+[k];

MA := MA-[a[i]];

write(fout, '(', k, ',', a[i], ') ');

end;

writeln(fout);

end;

procedure generare(i: Vf);

var j: Vf;

begin

if i = n-1 then

determina_arbore

else

for j := 1 to n do

begin

a[i] := j;

generare(i+1);

end;

end;

begin

write('Introduceti numarul de varfuri '); readln(n);

a[n-1] := n;

NrArb := 0;

assign(fout,'arbnvf.out');

rewrite(fout);

generare(1);

close(fout);

end.

De exemplu, pentru n=4, continutul fisierului de iesire va fi:

Arborele nr. 1 :(2,1) (1,1) (3,4)

Arborele nr. 2 :(3,1) (1,2) (2,4)

Arborele nr. 3 :(2,1) (1,3) (3,4)

Arborele nr. 4 :(2,1) (1,4) (3,4)

Arborele nr. 5 :(3,2) (2,1) (1,4)

Arborele nr. 6 :(1,2) (2,2) (3,4)

Arborele nr. 7 :(1,2) (2,3) (3,4)

Arborele nr. 8 :(1,2) (2,4) (3,4)

Arborele nr. 9 :(2,3) (3,1) (1,4)

Arborele nr. 10 :(1,3) (3,2) (2,4)

Arborele nr. 11 :(1,3) (2,3) (3,4)

Arborele nr. 12 :(1,3) (2,4) (3,4)

Arborele nr. 13 :(2,4) (3,1) (1,4)

Arborele nr. 14 :(1,4) (3,2) (2,4)

Arborele nr. 15 :(1,4) (2,3) (3,4)

Arborele nr. 16 :(1,4) (2,4) (3,4)

program Operatii_pe_arbori_binari;

const NrMaxVf = 20;

type Vf = 0..NrMaxVf;

ArboreBinar = ^NodArboreBinar;

NodArboreBinar = record

inf: char;

st, dr: ArboreBinar;

end;

var n: Vf;

fin, fout: text;

A: ArboreBinar;

function CreareArbore(x: Vf): ArboreBinar;

var rad: ArboreBinar;

begin

if x = 0 then

CreareArbore := nil

else

begin

new(rad);

read(fin, rad^.inf);

rad^.st := CreareArbore(x div 2);

rad^.dr := CreareArbore(x-x div 2 -1);

CreareArbore:=rad;

end;

end;

procedure preordine(rad: ArboreBinar);

begin

if rad <> nil then

begin

write(fout, rad^.inf);

preordine(rad^.st);

preordine(rad^.dr);

end

end;

procedure postordine(rad: ArboreBinar);

begin

if rad <> nil then

begin

postordine(rad^.st);

postordine(rad^.dr);

write(fout, rad^.inf);

end

end;

procedure inordine_iterativ(rad: ArboreBinar);

type Stiva = ^NodStiva;

NodStiva = record

inf: ArboreBinar;

urm: Stiva

end;

var S, p: Stiva;

NodCurent: ArboreBinar;

begin

write(fout, 'Parcurgerea inordine: ');

S := nil;

NodCurent := rad;

repeat

while NodCurent <> nil do

begin

new(p); p^.inf := NodCurent; p^.urm := S; S := p;

NodCurent := NodCurent^.st;

end;

if S <> nil then

begin

p := S; S := S^.urm;

write(fout, p^.inf^.inf);

NodCurent := p^.inf^.dr;

dispose(p);

end;

until (S = nil) and (NodCurent = nil);

writeln(fout);

end;

procedure parcurgere_pe_niveluri(rad: ArboreBinar);

type Coada = ^NodCoada;

NodCoada = record

inf: ArboreBinar;

urm: Coada

end;

var IncC, SfC, p, q: Coada;

begin

write(fout, 'Parcurgerea pe niveluri: ');

if rad <> nil then

begin

new(IncC); IncC^.inf := rad; IncC^.urm := nil; SfC := IncC;

while IncC <> nil do

begin

p := IncC;

write(fout, p^.inf^.inf);

if p^.inf^.st <> nil then

begin

new(q); q^.inf := p^.inf^.st; q^.urm := nil;

SfC^.urm := q; SfC := q

end;

if p^.inf^.dr <> nil then

begin

new(q); q^.inf := p^.inf^.dr; q^.urm := nil;

SfC^.urm := q; SfC := q

end;

IncC := IncC^.urm;

dispose(p)

end;

end;

writeln(fout)

end;

function max(a, b: integer): integer;

begin

if a > b then max := a

else max := b

end;

function inaltime(rad: ArboreBinar): integer;

begin

if rad = nil then

inaltime := -1

else

inaltime := max(inaltime(rad^.st), inaltime(rad^.dr))+1;

end;

begin

assign(fin,'opbin.in'); reset(fin);

assign(fout,'opbin.out'); rewrite(fout);

readln(fin,n);

A:=CreareArbore(n);

close(fin);

write(fout,'Parcurgerea preordine: '); preordine(A);

writeln(fout);

write(fout,'Parcurgerea postordine: '); postordine(A);

writeln(fout);

inordine_iterativ(A);

parcurgere_pe_niveluri(A);

writeln(fout, 'Inaltimea arborelui este: ', inaltime(A));

close(fout);

end.

program Constructie_Arbore_Binar;

const NrMaxVf = 20;

type Vf = 0..NrMaxVf;

ArboreBinar = ^NodArboreBinar;

NodArboreBinar = record

inf: Vf;

st, dr: ArboreBinar;

end;

Parcurgere = array[Vf] of Vf;

var A: ArboreBinar;

i: Parcurgere;

n: Vf;

fout: text;

function ConstrArb(rad, st, dr: Vf): ArboreBinar;

var r: ArboreBinar;

IPozRad: Vf;

begin

new(r); r^.inf := rad;

IPozRad := st;

while i[IPozRad] <> rad do inc(IPozRad);

if IPozRad = st then

r^.st := nil

else

r^.st := ConstrArb(rad+1,st,IPozRad-1);

if IPozRad = dr then

r^.dr := nil

else

r^.dr := ConstrArb(rad+IPozRad-st+1,IPozRad+1,dr);

ConstrArb := r;

end;

procedure Citire;

var k: Vf;

fin: text;

begin

assign(fin,'pi.in'); reset(fin);

readln(fin,n);

for k := 1 to n do read(fin, i[k]);

readln(fin);

close(fin);

end;

procedure preordine(rad: ArboreBinar);

begin

write(fout, rad^.inf, '(');

if rad^.st <> nil then preordine(rad^.st);

write(fout, ',');

if rad^.dr <> nil then

preordine(rad^.dr);

write(fout, ')');

end;

procedure AfisareArb;

begin

assign(fout,'pi.out'); rewrite(fout);

if A = nil then

write(fout, 'Arbore vid')

else

preordine(A);

writeln(fout);

close(fout);

end;

begin

Citire;

if n > 0 then

A := ConstrArb(1, 1, n)

else

A := nil;

AfisareArb;

end.

De exemplu, pentru fisierul de intrare:

fisierul de iesire va fi:

program Numar_Arbori_Binari_Distincti;

var NrVf, i: byte;

NrArb: extended;

begin

write('Introduceti numarul de varfuri '); readln(NrVf);

NrArb := 1;

for i := 2 to NrVf do

NrArb := NrArb*(NrVf+i)/i;

writeln('Nr. de arbori binari distincti cu ',NrVf,'varfuri: ');

writeln(NrArb:50:0);

readln

end.