Metoda Backtracking - Exemplu - problema reginelor

Metoda Backtracking

I.1.1         Descrierea metodei

Metoda Backtracking se aplica atunci cand solutia problemei de programare poate fi reprezentata sub forma unui vector X cu n elemente, X=, unde fiecare componenta x_k ia valori intr-o multime finita S_k. Fie n_k cardinalul multimii S_k, asadar n_k< . Spatiul S=S₁XS₂X.XS_n se numeste spatiul solutiilor posibile. In problemele concrete, intre componentele x_k ale unei solutii posibile XIS exista anumite relatii, numite conditii interne. Solutiile posibile ale caror componente satisfac conditiile interne se numesc solutii rezultat.

Trebuie mentionat inca de acum faptul ca in multe probleme practice multimile S_1, S₂.,S_n coincid, deci spatiul solutiilor posibile este de forma Sⁿ.

O idee de rezolvare consta in generarea tuturor solutiilor posibile si alegerea, dintre acestea, numai a acelora care satisfac conditiile interne. O asemenea abordare ar necesita un spatiu de memorie si un timp de calcul nejustificat de mari: pentru o problema cu caracter binar, in care n_k =2, pentru orice k, am genera 2ⁿ solutii posibile, dintre care numai o parte satisfac conditiile interne. Asadar, un algoritm elaborat astfel nu are nici o valoare practica.

Metoda Backtracking urmareste generarea progresiva numai a posibilelor solutii rezultat. Se porneste de la o solutie vida si se adauga in ea elemente, de la stanga spre dreapta, cata vreme sunt indeplinite conditiile interne. Daca la un moment dat nu mai sunt sanse sa se ajunga la o solutie rezultat, se incheie generarea solutiei cu acel prefix (pre-solutie) si se revine la reasignarea elementului anterior. De aici provine si numele metodei-generare cu revenire.

Metoda Backtracking poate fi reprezentata sub forma unui arbore de stare in care fiecarui nivel ii corespunde o alegere in spatiul solutiilor, alegere ce depinde de starea de pe nivelul anterior. Arborele de stare are urmatoarele proprietati:

Radacina semnifica o solutie vida;

Fiecare nod aflat pe nivelul k reprezinta o pre-solutie in care au fost asignate primele k componente. Daca pre-solutia verifica solutiile interne si nu este finala (k<n), atunci nodul corespunzator ei va avea cel mult n_k+1=card(S_k+1) fii. Arborele de stare are n niveluri (excluzand radacina), n fiind dimensiunea solutiei;

Frunzele de pe nivelul n (excluzand radacina) al arborelui sunt solutiile rezultat (pre-solutii pentru care s-a ajuns la k=n).

Timpul de calcul

Este important de precizat ca, desi metoda Backtracking reduce cautarea in spatiul solutiilor posibile, timpul de calcul necesar este -asa cum vom vedea mai jos- de ordin exponential, ceea ce face ca metoda sa nu fie recomandata practic decat atunci cand nu se gaseste o alta solutie cu timp polinomial.

I.1.2         Exemplu - problema reginelor

O problema clasica ce caracterizeaza metoda Backtracking este problema celor 8 regine. Cerinta problemei este de a aseza pe o tabla de sah de dimensiune 8X8, 8 regine care sa nu se atace intre ele. Reamintim ca regina este cea mai puternica piesa de sah, ea atacand tot ce se afla pe aceeasi linie, coloana sau diagonala cu ea. Problema poate fi generalizata pentru o tabla de sah cu n linii si n coloane pe care trebuie asezate n regine.

Pentru simplitate, in cele ce urmeaza vom considera problema reginelor pentru n=4.

Daca s-ar incerca asezarea "orbeasca" a n regine pe o tabla n², am obtine

posibilitati, ceea ce inseamna, pentru n=4, ,14*15*16=3360 de posibilitati, intre care, asa cum vom vedea mai jos, numai doua verifica conditiile interne.

Acest numar poate fi redus substantial daca observam ca pe fiecare coloana va fi asezata exact o regina (plasarea pe aceeasi coloana a doua regine le va face sa se atace si cum avem n coloane si n regine este evident ca fiecare coloana va contine exact o regina). O noua incercare de a le plasa "orbeste" va necesita nⁿ posibilitati de a aseza cate o regina pe fiecare coloana, ceea ce inseamna, pentru n=4, 256 de posibilitati.

In scopul de a reduce cat mai mult numarul de incercari, vom utiliza metoda Backtracking. Astfel, observam ca solutia poate fi reprezentata sub forma unui vector X cu n elemente (n fiind dimensiunea problemei: numarul de linii/coloane al tablei de sah, respectiv numarul de regine): X=, unde fiecare componenta x_k reprezinta linia reginei de pe coloana k. Asadar x_k va lua valori intr-o multime S_k= cu n elemente, deci finita.

Asadar, dupa modul in care a fost reprezentata solutia, fiecare regina k=1..n va fi plasata pe linia x_k si coloana k.

Conditiile interne ale problemei sunt date de faptul ca nu poate fi plasata o noua regina pe aceeasi linie sau diagonala cu cele deja plasate (conditia de coloana se verifica din modul de definire a solutiei). Tinand cont de modul in care a fost definita solutia problemei, conditia interna poate fi formalizata cu usurinta:

doua regine i si k sunt pe aceeasi coloana daca i=k, desi din modul in care se va construi solutia nu se va ajunge niciodata la verificarea acestui lucru;

doua regine i si k sunt pe aceeasi linie daca x_i=x_k;

doua regine i si k sunt pe aceeasi diagonala daca panta dreptei ce le leaga este 1 sau -1, panta fiind data de raportul diferentelor coordonatelor lor pe orizontala, respectiv verticala, adica daca abs(i-k)=abs(x_i-x_k):

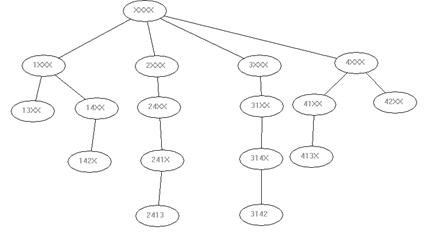
Fig. V . Reprezentarea arborescenta a spatiului solutiilor

O incercare de a genera toate posibilitatile ar duce la un arbore de stare cu 4⁴=256 de frunze si 1+4+4²+.+4ⁿ=(4ⁿ⁺¹-1)/(4-1)=(4⁵-1)/3=341 noduri, in timp ce cu metoda Backtracking au fost explorate numai 17 noduri. Cu toate acestea, din cauza dezvoltarii arborescente a spatiului solutiilor, metodei Backtracking i se asociaza un timp de calcul exponential, ceea ce face ca metoda sa nu fie recomandata decat atunci cand nu este posibila a rezolvare mai performanta.

I.1.3         Algoritmi de rezolvare

Pentru a trece la scrierea algoritmului, sa observam ca tehnica de lucru este urmatoarea:

se stabileste reprezentarea solutiei X= si spatiul solutiilor S=S₁XS₂X.XS_n;

se stabilesc, in functie de natura problemei, conditiile interne. Acestea nu intervin in elaborarea algoritmului, dar stau la baza definirii conditiilor de continuare a generarii solutiei. Se implementeaza functia de continuare: cont_k (x₁,x₂,.,x_k-1), pentru verificarea corectitudinii plasarii elementului x_k in continuarea pre-solutiei (x₁,x₂,.,x_k-1). Daca nu exista conditii interne atunci sunt generate toate perechile din S (toate elementele produsului cartezian);

se implementeaza functia de scriere a solutiei rezultat. In cazul in care se doresc retinerea numai a numitor solutii rezultat, aici se va face testarea;

se scrie algoritmul printr-o metoda iterativa sau recursiva, ca mai jos:

Varianta iterativa

In algoritmul de mai sus, cont_k (x₁,x₂,.,x_k-1) reprezinta verificarea conditiilor interne pentru pre-solutia de pe nivelul k: x₁,x₂,.,x_k-1, x_k.

Varianta recursiva

Varianta recursiva este mai putin performanta din punct de vedere al complexitatii, datorita utilizarii stivei, insa simplitatea ei constituie un avantaj semnificativ fata de varianta iterativa.

In ceea ce priveste complexitatea metodei, se poate observa cu usurinta ca in cazul in care nu exista solutie sau daca nu exista conditii interne, ceea ce determina generarea tuturor elementelor produsului cartezian S₁XS₂X.XS_n, metoda presupune explorarea intregului arbore. Presupunand ca toate multimile S_k au m elemente, arborele va avea mⁿ noduri terminale, ceea ce face ca metodei Backtracking sa i se asocieze un timp de calcul exponential.

I.1.4         Aplicatii

I.1.4.1   Problema reginelor

Sa se aseze pe o tabla de sah de dimensiune nXn, n regine care sa nu se atace intre ele.

Solutie:

Asa cum am aratat mai sus, plecand de la observatia ca pe fiecare coloana va fi asezata exact o regina, solutia va fi reprezentata sub forma unui vector X cu n elemente (n este dimensiunea problemei): X=, unde x_k= linia reginei k (de pe coloana k) S_k=, finita.

Problema reginelor-solutia recursiva

#include<iostream.h>

#include<math.h>

int nrSol=1;

int *X,n;

void retsol()

cout<<endl;

if(nrSol%5==0) cin.get();

int cont(int k)

void regine(int k)

main()

Observatii:

In implementarea de mai sus solutiile problemei sunt afisate sub forma de matrici cu nXn campuri cu valorile: "-" daca campul este liber, respectiv "X" daca campul contine o regina.

Solutiile au fost afisate cate 5 pe pagina. Variabila statica nrSol este un contor pentru solutiile rezultat. Pentru n=8, problema reginelor are 92 de solutii.

Daca se doreste afisarea numai a primei solutii, dupa apelul functiei retsol() in functia regine(), se va include instructiunea de iesire return, astfel:

if(k==n)

Implementarea recursiva a algoritmului Backtracking este mult mai avantajoasa ca efort de programare, datorita simplitatii si naturaletei ei, cu toate acestea varianta iterativa prezentata mai jos este optima din punctul de vedere al eforului de calcul si memoriei suplimentare utilizate.

Problema reginelor-solutia iterativa

void regineIt()

}

if(!bVerifica)

k--;

else

if(k==n)

retsol();

else

}

I.1.4.2   Problema turelor

Sa se aseze pe o tabla de sah de dimensiune nXn, n ture care sa nu se atace intre ele. Reamintim ca doua ture se ataca atunci cand se afla pe aceeasi linie sau coloana.

Indicatie: Cum si acum putem observa ca pe fiecare coloana se va afla exact o tura, solutia problemei este similara cu cea a reginelor, mai putin conditia de atac pe diagonala din functia de continuare. Pentru n=5, problema turelor are 120 de solutii.

I.1.4.3   Colorarea hartilor cu patru culori

Se considera harta a n tari si r culori. Sa se coloreze cele n tari cu cate o culoare (dintre cele r culori), astfel incat oricare doua tari vecine sa fie colorate diferit.

Indicatie: Se poate demonstra ca pentru a colora o harta cu n tari sunt suficiente 4 culori.

Solutie:

Pentru a reprezenta vecinatatile tarilor se va folosi o matrice patratica V, de dimensiune nXn, unde

Se observa imediat ca aceasta matrice este simetrica (daca i este vecina cu j, atunci si j este vecina cu i), ceea ce ne va permite sa populam si sa lucram cu doar o jumatate din matricea de vecinatati, am ales partea de sub diagonala principala. De asemenea, elementele de pe diagonala principala nu prezinta interes.

De exemplu, sa presupunem ca dorim sa coloram o harta micuta cu sase tari, ca in figura de mai jos:

Fig. V . Harta cu sase tari

Problema are solutie, o posibilitate de colorare este:

Fig. V . Colorarea tarilor cu 4 culori

unde a,b,c,d reprezinta cele 4 culori.

Matricea de vecinatati (adiacente) corespunzatoare hartii considerate va fi:

In continuare, vom reprezenta solutia problemei sub forma unui vector X cu n elemente (n fiind numarul de tari): X=, unde fiecare componenta x_k reprezinta culoarea ce va fi folosita pentru tara k. Asadar x_k va lua valori in multimea S_k= cu r elemente, deci finita.

Conditiile interne ale problemei sunt date de faptul ca nu poate fi folosita aceeasi culoare pentru doua tari vecine. Vom tine cont de faptul ca:

Doua tari i si k au aceeasi culoare: x_i =x_k

Doua tari i si k sunt vecine: V[i,k]=1.

Colorarea hartii folosind 4 culori

#include<iostream.h>

#include<math.h>

int nrSol=1;

int *X,**V,n,r=4;

char *culori[]=;

void retsol()

int cont(int k)

void harta(int k)

main()

harta(0);

for(i=0;i<n;i++)

delete V[i];

delete V;

delete[]X;

return 0;

Observatie: Pentru exemplul de mai sus cu n=6 tari exista 9 posibilitati de colorare cu 4 culori.

I.1.4.4   Alegerea drapelelor

Avand la dispozitie panza de sase culori: rosu, alb, galben, verde, portocaliu, albastru, se cere sa se genereze toate drapelele tricolore care indeplinesc conditiile:

Culorile de pe drapel sunt distincte;

Orice drapel are in mijloc culorile alb, galben sau portocaliu, in plus, aceste culori nu se pot afla in extremele drapelului.

Solutie:

Vom reprezenta solutia problemei sub forma unui vector X cu 3 elemente (numarul de culori intr-un drapel): X=, unde fiecare componenta x_k reprezinta culoarea folosita. Asadar x_k va lua valori in multimea S_k= cu nCulori elemente, deci finita.

Conditiile interne ale problemei sunt:

Nu se poate folosi aceeasi culoare de doua ori: x_i <>x_k, oricare i,k=1..3;

Culoarea din mijloc x₂ poate fi alb, galben sau potocaliu;

Culorile extreme x₁ si x₃     nu pot fi alb, galben sau potocaliu.

Drapele colorate

#include<iostream.h>

#include<math.h>

int nrSol=1;

int *X,n=3;

char*culori[]=;

int nCulori;

void retsol()

int cont(int k)

void drapele(int k)

main()

Observatie: In solutia prezentata mai sus s-a considerat ca dispunem de cantitati nelimitate de panza din fiecare culoare. Propunem cititorului sa implementeze o solutie in care cantitatile de panza sunt limitate.

I.1.4.5   Cavalerii Mesei Rotunde

La masa regelui Arthur stau asezati n cavaleri. La un moment dat, intre ei izbucneste un conflict in urma caruia fiecare cavaler se reaseaza la masa, astfel incat oricare doi vechi vecini nu mai sunt alaturati. Cum s-au asezat?

Solutie:

Sa ne imaginam ca fiecare cavaler are inscris pe scut un numar de ordine reprezentand pozitia sa initiala la masa (de la 1 la n). Practic, vom avea de generat o permutare a multimii in care sa nu existe doua elemente consecutive invecinate. Vom reprezenta solutia problemei sub forma unui vector X cu n elemente, unde fiecare componenta x_k reprezinta noua pozitie (noul scaun) a cavalerului k la masa. Asadar x_k va lua valori in multimea S_k= finita, deci putem aplica metoda Backtracking.

Pentru n=5, o posibila rearanjare este:

Fig. V .Cavalerii mesei rotunde

corespunzatoare solutiei: X=.

Conditiile interne ale problemei sunt:

Fiecarui cavaler i se asociaza un singur scaun (nu pot sta doi cavaleri pe acelasi scaun): x_i<>x_k, oricare i, k=1..n;

Doi vechi vecini nu mai pot sta alaturi:     x_k-x_k-1<>1 oricare k=2..n si, tinand cont de faptul ca masa este rotunda: x_n-x₀<>1.

Cavalerii mesei rotunde

#include<iostream.h>

#include<math.h>

int nrSol=1;

int *X,n;

void retsol()

cout<<endl;

if(nrSol%5==0) cin.get();

int cont(int k)

void Arthur(int k)

main()

I.1.5         Aplicatii ale metodei Backtracking in combinatorica

Metoda Backtracking poate constitui un instrument util si pentru a genera diferite elemente de combinatorica, asa cum vom vedea in sectiunea care urmeaza.

I.1.5.1   Reprezentarea submultimilor

Fie A= o multime cu n elemente si fie B o submultime a sa. Exista mai multe modalitati de a reprezenta submultimea B:

printr-un vector cu p componente, ce va contine cele p elemente ale submultimii B; se poate utiliza un vector cu n elemente in care elementele submultimii B vor fi plasate la inceput, iar restul elementelor vor fi vor avea o valoare ce nu se gaseste in A;

printr-un vector caracteristic V, in care elementele sunt date de relatia:

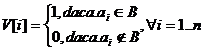
In functie de scopul urmarit, in problemele de generare de submultimi sunt posibile situatiile:

ordinea elementelor submultimii este relevanta;

ordinea elementelor submultimii este arbitrara, in acest caz elementele vor fi considerate in ordine crescator-lexicografica.

Pentru ca intre o multime finita A cu n elemente si multimea exista o bijectie, in cele ce urmeaza vom presupune ca multimea A are elementele 1,2,.,n. In practica trecerea de la multimea A considerata si cea originala se face considerand elementele submultimilor lui A ca indici in multimea A originala.

I.1.5.2   Generarea produsului cartezian

Fie A=A₁XA₂X.XA_n n multimi unde fiecare A_i are n_i elemente. Generarea elementelor produsului cartezian presupune generarea tuturor celor perechi de forma (a₁, a₂,., a_n), unde fiecare a_iIA_i

Generarea produsului cartezian

#include <iostream.h>

void ret_sol(int *X, int n)

void prodcart(int *N, int *X, int n, int k)

for(int i=0;i<N[k];i++)

}

main()

prodcart(N,X,n,0);

delete N;delete X;

return 0;

I.1.5.3   Generarea tuturor submultimilor unei multimi

Exista mai multe metode de a genera toate submultimile unei multimi. Vom prezenta aici o varianta ce utilizeaza vectorul caracteristic. Practic, a genera o submultime a unei multimi cu n elemente este echivalent cu a genera un vector (caracteristic) cu n elemente din :

XIⁿ.

Rezolvarea este similara cu cea a generarii produsului cartezian in care toate multimile A_i sunt .

Generarea tuturor submultimilor unei multimi

#include <iostream.h>

void ret_sol(int *X, int n)

void submult(int *X, int n, int k){

if(k==n) ret_sol(X, n);

else{

// se parcurge multimea Sk=

for(int i=0;i<2;i++)

}

main()

I.1.5.4   Generarea permutarilor elementelor unei multimi

Generarea permutarilor unei multimi A cu n elemente presupune generarea tuturor celor n! modalitati de a rearanja elementele lui A. Solutia problemei va fi reprezentata sub forma unui vector X cu n elemente, unde fiecare x_k va fi indicele elementului preluat din A.

ex.: pentru n=3 avem 3!=6 permutari:

2 3

Rezolvarea problemei consta in generarea tuturor multimilor X cu n elemente: 1,2,,n.

Generarea permutarilor elementelor unei multimi

#include <iostream.h>

int cont(int *X, int n, int k)

void ret_sol(int *X, int n)

void permR(int *X, int n, int k)

for(int i=1;i<=n;i++)

}

void permI(int *X, int n)

if(!c) k--;

else

if(k==n-1) ret_sol(X,n);

else

}

main()

I.1.5.5   Generarea aranjamentelor elementelor unei multimi

Daca A este o multime cu n elemente, generarea aranjamentelor cu p elemente ale ei consta in generarea tuturor celor n!/(n-p)! submultimilor sale cu p elemente care difera intre ele fie prin natura elementelor, fie prin ordinea lor. Solutia va fi reprezentata sub forma unui vector X cu p componente, fiecare element x_k fiind indicele elementului corespunzator preluat din A.

ex.: pentru n=3 si p=2 avem urmatoarele sase aranjamente:

2

Practic, rezolvarea problemei este similara cu generarea permutarilor in care insa ne vom opri atunci cand vectorul rezultat are p elemente.

Generarea aranjamentelor elementelor unei multimi

#include <iostream.h>

int cont(int *X, int n, int k)

void ret_sol(int *X, int n)

void aranj(int *X,int n,int p,int k)

for(int i=1;i<=n;i++)

}

main()

I.1.5.6   Generarea combinarilor elementelor unei multimi

Daca A este o multime cu n elemente, generarea combinarilor de p elemente ale ei consta in generarea tuturor celor submultimi ale sale cu p elemente care difera intre ele prin natura elementelor. Ordinea elementelor intr-o submultime este nesemnificativa, insa pentru a evita generari repetate ale solutiilor, vom considera elementele dintr-o combinare in ordine lexicografica crescatoare. Solutia va fi reprezentata sub forma unui vector X cu p componente, fiecare element x_k fiind indicele elementului corespunzator preluat din A. De exemplu, se cere formarea unei delegatii de k persoane dintre care l femei, cu angajatii unei sectii de n persoane, intre care p femei.

Ex.: pentru n=3 si p=2 avem urmatoarele trei combinari:

2

Rezolvarea problemei este similara cu generarea aranjamentelor, insa pentru ca la combinari ordinea elementelor nu prezinta interes, pentru a nu genera o solutie de mai multe ori vom considera elementele in ordine crescator-lexicografica.

Generarea combinarilor elementelor unei multimi

#include <iostream.h>

int cont(int *X, int n, int k)

void ret_sol(int *X, int n)

void comb(int *X, int n, int p, int k)

for(int i=1;i<=n;i++)

}

main()

I.1.5.7   Partitiile unei multimi

Daca A este o multime finita, intelegem prin partitie a lui A un set A₁, A₂,., A_n de submultimi ale sale (numite clase):

A=A₁ A₂ A_n

astfel incat acestea sunt nevide si disjuncte doua cate doua.

Ex.: Daca A=, o partitie a sa este A=A₁ A₂ A₃, unde A₁=, A₂=, A₃=.

In practica sunt utilizate mai multe modalitati de reprezentare a partitiilor. Pentru a ramane in contextul oferit de metoda Backtracking, noi vom folosi un vector X cu n elemente, unde fiecare componenta x_k va reprezenta indicele clasei din care face parte elementul a_k:

x_k=i, daca a_k IA_i

Astfel, pentru exemplul de mai sus, partitia poate fi reprezentata: X=.

Pentru rezolvare, se va utiliza un indicator suplimentar, nc care va reprezenta numarul curent de clase ale partitiei. La fiecare nivel k avem doua posibilitati pentru a-l incarca pe x_k:

• fie il vom plasa pe a_k intr-o clasa care a mai fost folosita si trecem cu generarea mai departe, avand acelasi numar curent nc de clase;
• fie il plasam pe a_k intr-o clasa noua nc+1 si trecem mai departe cu numarul curent de clase marit cu o unitate.

Se observa ca elementele efective ale multimii A nu sunt semnificative, partitionarea fiind privita ca o grupare a indicilor elementelor din A. Pentru o multime A cu 3 elemente avem urmatoarele cinci partitionari posibile:

Partitiile unei multimi

#include <iostream.h>

void ret_sol(int *X, int n)

void clase(int *X, int n, int nc, int k)

for(int i=1;i<=nc;i++)

// daca pe ak il punem intr-o partitie noua

X[k]=nc+1;

clase(X,n,nc+1,k+1);// se continua generarea

}

main()