| CATEGORII DOCUMENTE |
Definitia 1.13
Un digraf G = (N, A) se numeste slab conex (sau conex) daca pentru oricare doua noduri distincte din N exista un lant care are aceste doua noduri drept extremitati.
Observatia 1.3
Notiunea de conexitate are sens si pentru grafuri neorientate.
Exemplul 1.12
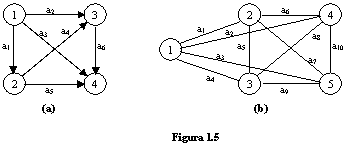
Digraful din figura 1.5 (a) si graful
neorientat din figura 1.5 (b) sunt conexe.
Definitia 1.14
Un subgraf G = (N , A ) al
unui digraf G = (N,A) se numeste componenta
conexa a lui G daca G este
conex si este maximal in raport cu incluziunea fata de
aceasta proprietate (oricare ar fi xI![]() = N-N ,
subgraful G x generat
de N x = N nu este conex).
= N-N ,
subgraful G x generat
de N x = N nu este conex).
Definitia 1.15
Un digraf G = (N,A ) se numeste arbore daca este fara cicluri si conex. Un digraf G = (N,A ) se numeste padure daca este fara cicluri.
Observatia 1.4
Un digraf G = (N, A ) este o padure daca fiecare componenta conexa a lui G' este un arbore. Notiunile de arbore si padure au sens si pentru grafuri neorientate.
Exemplul 1.13
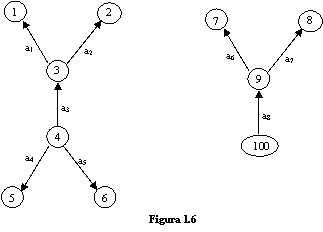
Digraful reprezentat in figura 1.6 este o
padure compusa din doi arbori. Daca se ignora sensul
arcelor se obtine o padure formata din doi arbori
neorientati.
Definitia 1.16
Un digraf G = (N, A) se numeste tare conex daca pentru oricare doua noduri distincte x, y din N exista un drum de la x la y si un drum de la y la x.
Observatia 1.5
Notiunea de tare conexitate are sens numai pentru grafuri orientate.
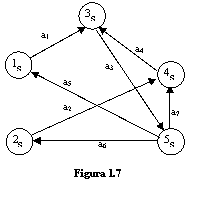
Exemplul 1.14
Digraful din figura 1.7 este tare conex.
Definitia 1.17
Un subgraf G = (N , A ) al
unui digraf G = (N, A) se numeste componenta
tare conexa a lui G daca G este tare conex si este
maximal in raport cu incluziunea fata de aceasta proprietate
(oricare ar fi xI![]() = N - N , subgraful G x generat de N x = N nu este tare conex).
= N - N , subgraful G x generat de N x = N nu este tare conex).
Definitia 1.18
Un nod r al digrafului G = (N, A) se numeste nod radacina daca pentru oricare alt nod x din N exista un drum de la r la x.
Observatia 1.6
Notiunea de nod radacina are sens numai pentru grafuri orientate. Un nod radacina nu exista intotdeauna.
Exemplul 1.15
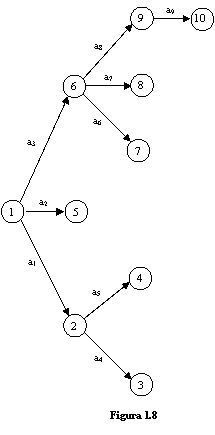
Nodul 1 al digrafului din figura 1.8 este nod radacina.
Definitia 1.19
Un digraf G = (N, A) se numeste quasi tare conex daca pentru oricare doua noduri x, y din N exista un nod z din N (care poate sa coincida cu x sau y) de la care pleaca un drum care ajunge la x si un drum care ajunge la y.
Observatia 1.7
Un digraf tare conex este quasi tare conex. Reciproca nu este adevarata.
Un digraf quasi tare conex este conex. Reciproca nu este adevarata.
Exemplul 1.16
Digraful din figura 1.8 este quasi tare conex.
Definitia 1.20
Un digraf G = (N, A ) se numeste arborescenta daca este fara cicluri si quasi tare conex.
Observatia 1.8
Notiunea de arborescenta are un sens numai pentru grafuri orientate.
Exemplul 1.17
Digraful din figura 1.8 este o arborescenta.
O arborescenta G = (N, A ) se mai numeste si arbore radacina.
Un arbore radacina se poate reprezenta pe niveluri in modul urmator: pe nivelul 0 se reprezinta nodul radacina r si pe nivelul k se reprezinta nodurile x pentru care lungimea drumurilor de la r la x este egala cu k. In acest caz sageata de pe fiecare arc este omisa, deoarece sensul este de la nivelul k la k+1, pentru k = 0,1, ..
In continuare este prezentata terminologia pentru arborii radacina reprezentati pe niveluri.
Definitia 1.21
Lungimea drumului unic de la nodul radacina r la un nod y se numeste adancimea nodului y.
Adancimea nodului y, notata h(y), se poate defini recursiv in modul urmator:
![]()
Evident ca adancimea unui nod reprezinta nivelul acestui nod.
Definitia 1.22
Nodul x se numeste ascendent direct sau parinte al nodului y si nodul y se numeste descendent direct sau fiu al nodului x daca x este predecesor al nodului y, altfel spus, (x, y) I A . Nodurile y care au acelasi parinte x se numesc frati. Nodul x se numeste nod intern daca are cel putin un succesor si se numeste nod terminal sau nod frunza daca nu are nici un succesor.
Exemplul 1.18
Arborescenta din figura 1.8 este redata ca arbore radacina reprezentat pe niveluri in figura 1.9.
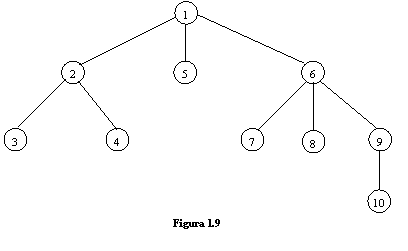
Avem: h(1) = 0, h(2) = h(5) = h(6) = 1, h(3) = h(4) = h(7) = h(8) = h(9) = 2, h(10) = 3, h(G ) = 3; nodul 1 este nod radacina, nodurile 1, 2, 6, 9 sunt noduri interne, nodurile 3, 4, 5, 7, 8, 10 sunt noduri terminale sau frunze; nodurile 7, 8, 9 sunt frati avand nodul 6 ca parinte.
Definitia 1.23
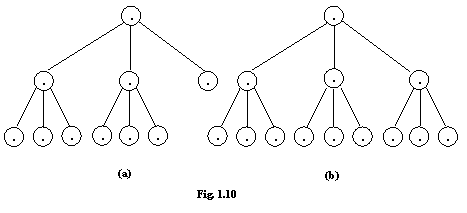
Un arbore radacina cu proprietatea ca fiecare nod are cel mult p succesori se numeste arbore p-ar. Un arbore p-ar se numeste complet daca fiecare nod intern are exact p succesori si se numeste plin daca fiecare nod intern are exact p succesori si toate nodurile terminale au aceeasi adancime.
Exemplul 1.19
Arborele din figura 1.9 nu este nici complet si nici plin.
Arborele ternar ( 3-ar ) reprezentat in figura 1.10(a) este complet dar nu este plin si arborele reprezentat in figura 1.10(b) este plin deci si complet.
Definitia 1.24
Un arbore radacina cu proprietatea ca succesorii fiecarui nod intern sunt ordonati, se numeste arbore ordonat. Daca ordinea nu este precizata, atunci implicit este de la stanga la dreapta.
![]()
![]()
Definitia 1.25
Se numeste arbore radacina un sir finit de forma G = (r, G , ., G t), unde r este nodul radacina, iar sirul G ,., G t este un sir finit, eventual vid, de subarbori radacina cu nodurile radacina r1, , rt succesori ai nodului r.
Definitia 1.26
Un sir finit, eventual vid, de arbori radacina se numeste padure pe care o notam cu G*, daca nu este vida si cu , daca este vida.
Observatia 1.9
Daca dintr-un arbore radacina G = (r, G , . ,G t) se elimina nodul radacina r si arcele incidente la acesta, atunci se obtine o padure G* = (G , , G t si arborele radacina G se poate exprima sub forma G = (r, G*).
Exemplul 1.20
Daca din arborele radacina reprezentat in figura 1.9, se elimina nodul radacina r = 1 si arcele (1,2), (1,5), (1,6) se obtine padurea G* = (G , G , G ), unde subarborii radacina G , G , G au nodurile radacina r1 = 2, r2 = 5, r3 = 6.
Definitia 1.27
Un arbore 2-ar ordonat pentru care fiecare succesor este denumit fie succesor stang, fie succesor drept se numeste arbore binar.
Se accepta si arborele binar vid. Daca se suprima nodul radacina r si arcele incidente la acest nod, arborii binari obtinuti se numesc subarborele stang, respectiv subarborele drept al radacinii r. Unul dintre acesti subarbori sau amandoi pot fi vizi. Notiunea de subarbore stang sau drept se aplica oricarui nod x al arborelui. Astfel, un arbore binar se poate defini si recursiv in modul urmator.
Definitia 1.28
Se numeste arbore binar un sir, fie vid notat , fie finit de forma G = (r, G , G ), unde r este nodul radacina si G , G sunt subarborele stang, respectiv subarborele drept ai nodului radacina r.
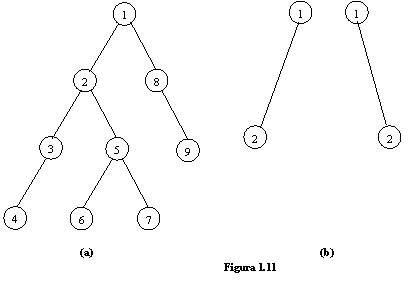
Exemplul 1.21
Arborele binar reprezentat in figura 1.11(a) are r = 1, subarborele stang G are nodul radacina r1 = 2 si subarborele drept G are nodul radacina r2 = 8. Nodul x = 3 are subarborele stang format numai din nodul radacina r = 4 si subarborele drept este vid. In figura 1.11(b) sunt reprezentati doi arbori binari care sunt identici ca arbori radacina, dar sunt distincti ca arbori binari, deoarece arborii binari sunt arbori radacina ordonati si nodul 2 este succesorul stang respectiv succesorul drept al nodului radacina 1.
Definitia 1.29
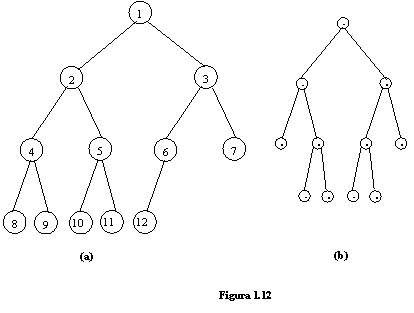
Un arbore binar G = (N, A ) se numeste perfect daca toate nodurile terminale sunt situate pe ultimele doua niveluri in modul urmator: penultimul nivel q - 1 este plin (are 2q-1 noduri) si pe ultimul nivel q nodurile terminale sunt grupate cel mai la stanga posibil.
Exemplul 1.22
Arborele binar din figura 1.12(a) este perfect, dar nu este complet. Arborele binar din figura 1.12(b) este complet, dar nu este perfect.
Nodurile unui arbore binar perfect sunt numerotate intr-o ordine ierarhica perfecta care consta in a numerota in ordine crescatoare, plecand de la 1, toate nodurile arborelui binar perfect in ordinea crescatoare a nivelurilor si pe fiecare nivel numerotarea se face de la stanga la dreapta.
Exemplul 1.23
Arborele binar perfect reprezentat in figura 1.12(a) are nodurile numerotate in ordine ierarhica perfecta.
Observatia 1.10
Daca intr-un arbore binar perfect un nod este numerotat prin k in numerotarea ierarhica perfecta, atunci succesorul sau stang este numerotat prin 2k iar succesorul sau drept prin 2k+1.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1617
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved