LISTE - Sortare prin selectie

lISTE - Sortare prin selectie

Spre deosebire de sortarea prin insertie, unde inregistrarile erau luate in considerare una dupa alta, la tehnica sortarii prin selectie inregistrarile trebuie sa fie toate prezente pe mediul de intrare inainte de inceperea sortarii.

Vom prezenta doi algoritmi de sortare din aceasta clasa: - sortarea prin selectie directa si sortarea prin selectie arborescenta.

1. Sortarea prin selectie directa

In acest caz inregistrarile ce trebuie sortate sunt organizate liniar sub forma de lista simplu inlantuita.

Algoritmul este insa valabil pentru o alocare secventiala a inregistrarilor simplu inlantuite.

In principiu metoda sortarii prin selectie directa este urmatoarea: se repeta dupa i=1, 2, , n-1 si se executa actiunile:

a) se cauta inregistrarile cu cheia cea mai mica de la inregistrarea "i" la inregistrarea "n", fie ea cu numarul de ordine "j".

b) se interschimba inregistrarile Ri si Rj

Pentru implementarea algoritmului, structura elementelor listei va fi urmatoarea:

typedefstruct lista

plist;

De asemenea va fi necesara introducerea unei noi operatii asupra elementelor listei: - interschimbarea a doua inregistrari din cadrul listei.

Refacerea legaturilor pentru interschimbare in cazul a doua inregistrari ce nu sint extremele listei, este urmatoarea:

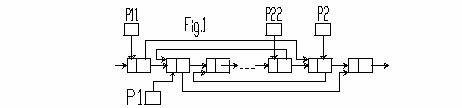
Notind cu p1 si p2 pointerii ce indica spre elementele ce urmeaza a fi interschimbate si cu p11, respectiv p22 pointerii spre elementele anterioare, actiunea de interschimbare se poate descrie astfel (p este o variabila de referinta auxiliara):

p:=p2->l;

p2->l:=p1->l;

p22->l:=p1;

p1->l:=p;

p11->l:=p2;

In cazul, cind primul element ce urmeaza a fi schimbat este primul element al listei, trebuie modificat si pointerul ce indica spre capul listei. Deci, in loc de p11->l:=p2 va trebui scris p0:=p2, unde p0 este pointerul ce indica spre capul listei.

Programul de sortare prin selectie directa poate fi scris in felul urmator (cheile si informatia utila a inregistrarilor de sortat se gasesc intr-un fisier text):

#include <stdlib.h>

#include <alloc.h>

#include <conio.h>

#include <stdio.h>

typedef struct lista

plist;

plist *p0, *p1, *p2, *p11, *p22, *p, *pp;

int min;

void creare(FILE *f)

void inters(plist *p11, plist *p22)

else

void main()

p = p->l;

}

if (min<p1->k) inters(p11,p22);

if (p11==NULL) p11 = p0;

else p11 = p11->l;

p1 = p11->l;

printf('Inregistrarile sortate sint: n');

p = p0;

while (p!=NULL)

Procedura 'creare' creaza lista simplu inlantuita a inregistrarilor, citind cheile si informatia utila din fisierul 'asde.dat', iar procedura 'inters' schimba in lista pozitia elementelor ce urmeaza dupa cele indicate de pointerii p11 si p22.

2. Selectia arborescenta

Principiile sortarii prin selectie arborescenta sint usor de inteles prin asemanarea cu meciurile unui 'turneu prin eliminare'.

Presupunem initial jucatorii cuplati doi cite doi. In primul tur cistiga acei jucatori care au acumulat puncte de penalizare mai putine. Apoi iarasi se cupleaza cite doi si cistigatorii se califica in mod asemanator in turul urmator. Va cistiga in final jucatorul cu cel mai mic numar de puncte de penalizare.

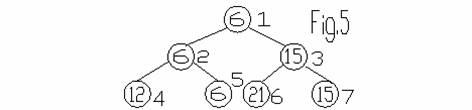
Un exemplu este dat in figura urmatoare:

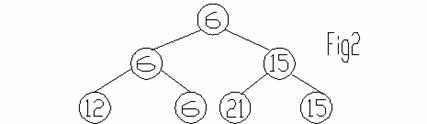
Am codificat patru jucatori cu urmatoarele punctaje: 12,6, 21,15. S-a realizat astfel o structura arborescenta (un arbore binar) in virful careia se afla jucatorul cu cel mai mic punctaj de penalizare. S-a sortat astfel cel mai mic element din sirul de intrare (12,6,21,15), doi cate doi.

Pentru a afla urmatorul punctaj, se observa ca nu este obligatoriu ca acesta sa fie al jucatorului din 'semifinala' (15 puncte). Este necesara inlocuirea punctajului jucatorului cistigator cu un numar mai mare decit punctajul oricarui jucator (desemnam acest punctaj cu +), el nu va fi cu siguranta selectat in turul urmator.

Se reface astfel calculul in modul urmator indicat de figura de mai jos:

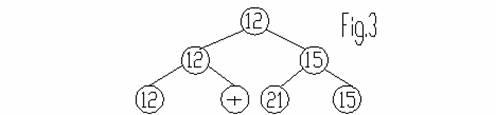
S-a gasit astfel al doilea punctaj in ordinea crescatoare 12.

Procedeul se continua inlocuind acum punctajul 12 cu + si se va selectiona cel de al treilea numar in ordine crescatoare 15, iar apoi ultimul punctaj selectionat va fi 21.

Procedeul se incheie cind in nodurile arborelui nu se va afla decit simbolul + .

Aceasta metoda de sortare este o metoda ce pleaca de la baza spre virf. Ea este foarte simpla, insa implementarea ei se face pe baza arborilor binari. Pentru a putea realiza operatiile specificate, vor trebui luate suplimentar intr-o lista liniara toate elementele de pe acelasi nivel.

Va rezulta o structura de genul urmator:

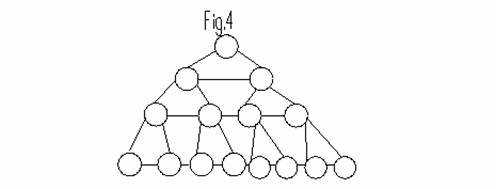
Un element al unei asemenea structuri va putea fi descris astfel:

typedef struct nod

pnod;

unde cimpurile 'left', 'right' si 'next' reprezinta pointerii respectiv spre descendentul din stinga, descendentul din dreapta si spre elementul urmator din acelasi nivel.

Pentru a putea exploata facilitatile arborilor binari si a folosi o metoda de sortare de la virf spre baza, se poate renunta la cimpul 'next', structura devenind un arbore binar, insa trebuie modificat algoritmul de mai sus.

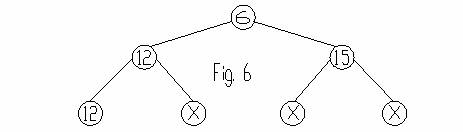
Se observa in fig. 2 ca orice nod din arbore are o cheie cu valoarea mai mica sau egala cu cea a fiecarui descendent. Putem numerota nodurile astfel:

Notind cu 'i' indicele nodurilor si cu 'ki' cheile atasate respectivelor noduri, se observa ca avem relatiile:

k_i<=k_2i

k_i<=k_(2i+1)

Presupunind ca avem 'n' noduri in arbore, relatiile de mai sus se mai scriu:

k[i/2]<=ki oricare ar fi 1<=(i/2)<i<=n

Un asemenea arbore se numeste 'ansamblu', (movila, sau 'heap').

Putem modifica ansamblul din fig. 5 astfel incit extragind elementul din virful arborelui si miscind in sus descendentul cu cheia cea mai mica, iar in locul acestuia procedind la fel, pina la ultimul nivel, arborele rezultat sa fie tot un ansamblu (heap), care sa aiba in virful sau elementul cu cheia cea mai mica dintre elementele ramase.

Procedind in acest mod, extragind pe rind elementele din virful arborelui acestea vor fi sortate deja.

Un asemenea ansamblu (heap) este prezentat in figura urmatoare:

Se observa ca in acest caz sint necesare mai putine noduri.

Tipul acesta de sortare, ale carei principii au fost enumerate mai sus se numeste sortare cu ansamble (sortare in movila). Algoritmul de sortare cuprinde doua parti distincte: - crearea ansamblului si apoi extragerea pe rind a elementului din virf a acestuia (odata cu urcarea pe nivelele ierarhice superioare a descendentilor cu cheia cea mai mica) pina cind ansamblul devine vid.

Un element al unui ansamblu va avea urmatoarea structura:

typedef struct heap

Am renuntat la cimpul 'i' de informatie utila, aceasta nefiind semnificativa deocamdata din punctul de vedere al algoritmului de sortare.

Algoritmul de construire al ansamblului nu este unic si nu are pretentie ca este cel mai performant. Printr-o analiza atenta a procesului de construire se pot elabora si alti algoritmi, posibil mai performanti decit cel prezentat. El va genera un arbore binar care poseda proprietatile unui ansamblu (cheia fiecarui nod din arbore este mai mica decit cheile fiecarui descendent), dar este posibil ca acesta sa fie neechilibrat pentru anumite succesiuni ale cheilor inregistrarilor ce urmeaza sa fie sortate.

Initial arborele este vid. Inregistrarile se introduc in arbore prin virful acestuia, deplasindu-se in jos spre stinga, sau spre dreapta eventualele inregistrari cu chei mai mari decit cheia nou introdusa. Aceste deplasari spre stinga sau spre dreapta se vor face alternativ, pentru a echilibra cit mai mult arborele ce se construieste. Pentru aceasta se foloseste o variabila inregistrare R ce poate lua valorile 1 si -1, dupa cum ultima inserare a fost facuta la descendentul sting sau drept al unui nod terminal din arbore.

In cadrul programului de sortare arborescenta, valorile cheilor inregistrarilor ce urmeaza sa fie sortate se presupune ca se citesc dintr-un fisier text, iar cheile inregistrarilor sortate se afiseaza pe terminal.

#include <stdio.h>

#include <alloc.h>

#include <stdlib.h>

typedef struct heap

pheap;

int lev;

pheap *p0;

FILE* f;

void creareh()

else

else

if (p->right == NULL)

else

if (r == 1) p = p->right

else p = p->left;

else

else

if (p->right == NULL)

else

if (r == 1) p = p->right;

else p = p->left;

}

} while (!(q == 1));

}

}

void hsort(void)

while (!((p->left == NULL) && (p->right == NULL)));

if (p1->left == p) p1->left = NULL;

else p1->right = NULL;

} while (!((p0->left == NULL) && (p0->right == NULL)));

a = p0->k;

printf('%dn',a);

void main()

Probleme propuse

1. Sa se scrie un program de sortare prin selectie directa folosind liste liniare dublu inlantuite.

2. Sa se scrie un program de sortare prin selectie arborescenta folosind o structura ca cea din fig. 4 si o metoda de sortare de la baza la virf.

3. Pentru gestiunea abonatilor unei centrale telefonice trebuie pastrate urmatoarele informatii referitoare la fiecare abonat: numele, prenumele, adresa (strada , numar), numar de telefon.

Se cere:

a) Sa se construiasca o lista dublu legata liniara cu numele, prenumele si telefonul abonatilor care au domiciliul pe o strada ce se afla intr-o lista liniara simplu inlantuita de strazi specificate;

b) Sa se ordoneze ultima lista dupa numele si prenumele abonatilor, iar pentru abonatii cu acelasi nume dupa numerele lor de telefon.

4. Se considera ca la recensamintul populatiei se iau in considerare urmatoarele informatii: nume, prenume, grupa de studii (primar, mediu, universitar), adresa (articol cu variante - strada si numarul sau strada, blocul, scara, etajul, apartamentul), virsta, sexul.

Se cere:

-Sa se creeze o lista liniara simplu legata cu persoanele avind un nume specificat, sex specificat, o grupa de studii specificata si locuiesc pe una din strazile unui aceluiasi cartier, specificate intr-o lista separata; sa se ordoneze apoi lista creata.

5. Se considera un sistem matematic specificat prin:

-un sir de identificatori care desemneaza axiomele sistemului;

-un sir de identificatori care desemneaza teoremele sistemului. Pentru fiecare teorema se specifica si multimea axiomelor si teoremelor ce intra in demonstratia sa.

Se cere:

Sa se ordoneze sirul de teoreme astfel incit pentru fiecare teorema, toate teoremele ce intra in demonstratia sa apara inaintea teoremei specificate.

6. Se considera doua liste liniare simplu legate cu cimpurile de informatie utila de tip sir de caractere.

Se cere sa se construiasca o lista care contine reuniunea celor doua liste si in care elementele sint ordonate crescator in raport cu ordinea lexicografica folosind o structura intermediara de tip arbore.

7. Orasele unei anumite regiuni sint caracterizate prin urmatoarele date: numele orasului, numarul de locuitori, aprecierea economica globala (ce poate fi A, B, C, D, E, cea mai buna este A) si suprafata in kilometri patrati.

Se cere:

Sa se ordoneze lista construita in ordine crescatoare, considerind ca ordinea importantei datelor referitoare la un oras (exceptind numele orasului) este cea precizata in enunt si sa se afiseze apoi lista ordonata (folosind HEAP-SORT).

8. Se considera o retea locala de calculatoare formata din servere si statii de lucru. Fiecare server sau statie de lucru este un calculator compatibil IBM-PC, model XT, AT, PS/1 sau PS/2. Pentru fiecare astfel de calculator intereseaza: tipul procesorului (poate fi 8088, 8086, 80286, 80386, 80486), modelul (oricare din cele 4 mentionate), capacitatea memoriei interne (in Mocteti), numarul de unitati de disc floppy, daca are sau nu harddisk si in caz afirmativ capacitatea acestuia si tipul de adaptor video (se considera ca poate fi oricare dintre: MDA, HERCULES, CGA, EGA sau VGA). Se considera ca reteaua are o structura de graf. Fiecare nod din graf reprezinta un calculator, iar fiecare legatura din graf o conexiune intre doua calculatoare. Reprezentarea grafului se face sub forma unei liste de adiacenta ce contine nodurile grafului si pentru fiecare nod lista vecinilor acestui nod. Fiecarui nod din graf i se asociaza un numar. Datele referitoare la calculatoare se pastreaza intr-o tabela, datele aferente calculatorului din nodul 'i' al retelei fiind plasate in elementul 'i' al tabelei.

Se cere:

a)Construirea structurilor de date corespunzatoare descrierii retelei;

b) Sortarea cu metoda HeapSort in ordine descrescatoare a listei de adiacenta dupa criteriile: server sau statie (se considera statie<server), model calculator (XT < AT < PS/1 < PS/2), tip procesor (8088 < 8086 < 80286 < 80386 < 80486), capacitate memorie interna, daca au sau nu harddisk (are>nu are) iar daca au harddisk in ordine descrescatoare a capacitatii acestuia.

9. Aceeasi problema de mai sus, dar se cere sortarea in ordine descrescatoare pentru fiecare nod din lista de adiacenta a listei vecinilor acestuia conform criteriului server_statie (vezi problema 8);

10. Se considera o grupa de studenti care au avut de sustinut in ultima sesiune n=5 examene. Pentru gestiunea rezultatelor obtinute in sesiune se alcatuieste o lista cu toti studentii grupei care pastreaza numele si prenumele fiecarui student si rezultatele obtinute de acesta. Facem observatia ca orice rezultat poate fi : o nota de promovare, cuprinsa intre 5 si 10, o nota insuficienta pentru promovare intre 1 si 4 sau poate specifica faptul ca studentul respectiv nu s-a prezentat la examenul respectiv.

Se cere sa se construiasca lista cu numele si prenumele studentilor si rezultatele obtinute de acestia in sesiune si sa se ordoneze dupa rezultate.

11. Aceeasi problema ca mai sus, dar se cere sa se construiasca lista studentilor integralisti, lista studentilor cu un examen nepromovat, lista studentilor cu 2 examene nepromovate si lista studentilor cu mai mult de 2 examene nepromovate, toate ordonate alfabetic si apoi sa se afiseze aceste liste.

12. Aceeasi problema ca la punctul 10 in care se cere sa se ordoneze lista studentilor integralisti dupa media la cele n=5 examene si sa se afiseze.