| CATEGORII DOCUMENTE |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
Matrice rare
Definire si moduri de reprezentare
Matricele reprezinta structuri de date reprezentate de tablouri unidimensionale, bidimensionale si multidimensionale ce sunt memorate sub forma unei zone continue de memorie, definita static sau dinamic de catre programator. Utilizarea acestei structuri de date in aplicatii software care rezolva probleme din diferite domenii ale societatii umane are avantajul implementarii unor algoritmi de prelucrare a datelor usor de inteles si care sunt definiti de metodele matematice de lucru cu matrice.
Cu toate ca evolutia tehnologiei hardware defineste limite din ce in ce mai inalte pentru memoria fizica si logica disponibila pe o platforma, producatorii de software urmaresc obtinerea unor niveluri maxime de optimizare a spatiului si a vitezei de prelucrare pentru programele lor. In cazul matricelor oarecare prelucrarea rapida este echivalenta cu definirea si implementarea unui algoritm performant care sa dea rezultatele cautate intr-un timp scurt si cu ocuparea unei zone de memorie mica.
Analiza datelor memorate in matrice a evidentiat dependenta dintre performanta si tipul acestora. Astfel s-a ajuns la concluzia ca daca o mare parte, peste 70%, din datele matricei nu afecteaza prelucrarile, se impune reprezentarea in memorie a matricei respective prin intermediul unei alte forme decat cea a unui masiv bidimensional. Pentru multe probleme a caror rezolvare impune utilizarea unui program ce implementeaza lucrul cu matrice, se considera ca fiind date neutre, elementele care au valoarea 0 si care nu influenteaza rezultatul final.
O matrice rara este o matrice in care numarul elementelor cu valoare diferita de 0 reprezinta mai putin de 30% din numarul total de elemente. Utilizarea unei matrice rare este dictata de problemele care se rezolva bine utilizand matrice, dar care sunt descrise de putine valori, astfel incat o mare parte din elementele matricei sunt utilizate ineficient, fiind initializate cu valoarea 0. Rezolvarea unei probleme de transport ce are asociat un graf descris de un numar mare de noduri si de un numar mic de drumuri necesita o matrice rara in cazul in care numarul legaturilor existente reprezinta un procent foarte mic din totalul legaturilor posibile.
Figura 1 descrie o matrice care este rara deoarece numarul elementelor nenule reprezinta 18% din totalul elementelor.
Fig. 1 Matrice rara
Daca se considera matricea rara MR, cu N elemente cu valoare diferita de zero, aceasta este reprezentata pentru a optimiza spatiul necesar memorarii, utilizand una din formele:
vector de N elemente de tip structura element_mat_rara care sa identifice elementele nenule prin valoarea si pozitia lor in matrice;
struct elemenr_mat_rara
trei vectori de dimensiune N utilizati pentru a memora valorile elementelor diferite de zero, linia, respectiv, coloana pe care se gasesc in matrice; daca parcurgerea matricei se realizeaza in ordinea liniilor, iar vectorii sunt numiti valoare, linie si coloana, atunci al i-lea element nenul are valoarea valoare[i] si se gaseste pe linia linie[i], respectiv, pe coloana coloana[i]; de exemplu matricei din figura 1 cu N = 9 elemente diferite de zero ii corespunde reprezentarea din figura 2;
|
vectorul valoare | ||||||||||
|
vectorul linie | ||||||||||
|
vectorul coloana |
Fig. 2. Reprezentarea matricei rara din figura 1 prin intermediul a trei vectori
de dimensiune N = 9 elemente.
o lista de n liste, unde n reprezinta numarul de linii al matricei, de dimensiuni variabile ce contin elemente de tip element_mat_rara2 pentru fiecare linie a matricei initiala; deoarece linia elementului nenul este data de numarul listei in lista de liste, nu mai este necesara memorarea acestei informatii; numarul total de elemente din cele n liste este egal cu numarul, N, de elemente diferite de zero din matrice;
struct elemenr_mat_rara2
figura 3 descrie modul de implementare a matricei descrisa in figura 1 utilizand lista de liste;
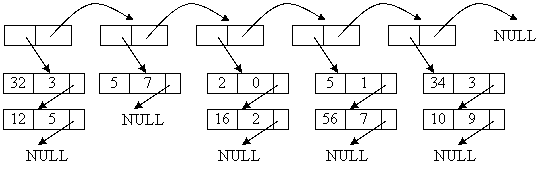
Fig. Implementarea matricei rara din figura 1 utilizand lista de liste.
Un tip particular de matrice rara este matricea banda. O matrice rara este de tip banda daca elementele diferite de zero sunt plasate in interiorul matricei catre mijlocul liniilor. Pentru o matrice patratica acest lucru este echivalent cu asezarea elementelor in jurul diagonalei principale. Figura 4 descrie o matrice banda MB, cu NB = 12 elemente nenule.
Fig. 4. Matrice rara de tip banda.
O forma de reprezentare a matricei din figura 4 utilizeaza trei vectori valori, col_start si col_stop pentru a memora secventele de elemente diferite de zero, indicele coloanei unde incep elementele cu valori nenule, respectiv indicele coloanei pe care se gaseste ultimul element din secventa de valori diferite de zero. Acest lucru este posibil pentru ca pe fiecare linie a matricei valorile nenule sunt considerate grupate, chiar daca intre ele se gasesc valori nule. Numarul de elemente din vectorii col_start si col_stop este dat de numarul de linii al matricei.
Figura 5 descrie modul de implementare a matricei banda utilizand aceasta forma de reprezentare.
|
vectorul valoari | |||||||||||||||
|
vectorul col_start | |||||||||||||||
|
vectorul col_stop |
Fig. 5. Reprezentarea matricei banda din figura 4.
Vectorii col_start, col_stop sunt utilizati pentru a determina coloana de start, respectiv, coloana de oprire a secventei de elemente diferite nenule de pe linia a i-a. De exemplu pe linia i = 3 secventa incepe pe coloana col_start[i] = 5 si se incheie cu elementul de pe coloana col_stop[i] = 7. Pentru a determina valoarea elementului MB[2][5], cu i=2 si j=5, se determina valoarea poz data de relatia:
![]()
iar valoarea elementului MB[2][5] este data de valori[poz]. Anterior, elementul cautat este validat prin verificarea relatiilor j ≤ col_stop[i] si j ≥ col_start[i].
Cu toate ca aceste forme de reprezentare descrise nu sunt singulare, avantajele utilizarii matricelor rare in una dintre aceste reprezentari sunt evidentiate in special de matricele de dimensiuni mari si foarte mari.
Construirea matricelor rare
Matricele rare sunt un tip particular de matrice si sunt reprezentate prin diferite forme de memorare. Cu toate acestea, ele se supun acelorasi reguli asemenea unei matrice oarecare implicata in operatii in care operanzii sunt de tip masiv. Din aceasta cauza, formele de reprezentare implica utilizarea de algoritmi diferiti ca abordare si grad de complexitate care sa realizeze diferite prelucrari pe matricea rara,.
Pentru a exemplifica operatiile pe matrice rare s-a construit clasa MatriceRara care implementeaza forma cu trei vectori, VectVal, VectCol si VectLin pentru a retine valoarea elementului nenul si pozitia sa in matrice. Matricea rara este definita de numarul total de elemente nenule, NrElem si de dimensiunea ei, numarul de linii, NrLinii, respectiv, numarul de coloane, NrColoane.
class MatriceRara
Crearea unui obiect de tip MatriceRara este realizata de cei trei constructori ai clasei, care permit construirea unei matrice rara:
lipsita de elemente:
MatriceRara::MatriceRara()
prin citirea de la tastatura a celor NrElem elemente nenule:
MatriceRara::MatriceRara(int nrElem, int nrLinii, int nrColoane)
}
prin verificarea unei matrice oarecare si preluarea elementelor diferite de zero:
MatriceRara::MatriceRara(int **Matrice,int n, int m)
}
else
}
Metoda din cadrul clasei care verifica caracterul unei matrice de a fi rara este:
int MatriceRara::verific(int **a,int n,int m)
Afisarea celor trei vectori ce descriu matrice rara, este realizata de metoda void afisare( ).
void MatriceRara::afisare ()
else
cout<<'Matrice vida !';
}
La constructia unei matrice rara trebuie sa se tina cont de modul de parcurgere al matricei initiale, fapt care afecteaza secventa de aparitie a valorilor in vectorul VectVal. Clasa MatriceRara utilizeaza parcurgerea la linii a matricei.
Operatii cu matrice rare
Rezolvarea unor probleme reale prin intermediul matricelor impune metode si tehnici complexe de lucru. La baza acestora se gasesc operatii elementare care au operanzi de tip matrice.
Matricele rare nu implica un comportament diferit in cadrul operatiilor, insa necesita o metoda particulara, dependenta de forma reprezentare, de acces la un element x[i][j].
Operatia de transpunere a unei matrice rara este realizata prin supraincarcarea operatorului ! care transpune matricea rara din obiectul de tip MatriceRara primit implicit. Cu toate ca operatia efectiva de transpunere implica parcurgerea vectorilor VectCol si VectLin si interschimbarea valorilor, trebuie avuta in vedere si sortarea celor trei vectori dupa valorile din VectLin si apoi din VectCol. Aceasta operatie suplimentara este echivalenta cu refacerea matricei initiale si crearea matricei rara prin parcurgerea pe linii a elementelor. Lipsa etapei de sortare conduce la o matrice rara construita prin parcurgerea pe coloane a matricei initiale si la obtinerea de rezultate eronate utilizand metodele clasei MatriceRara.
De exemplu, transpusa matricei rara din figura 2 este:
|
vectorul valoare | ||||||||||
|
vectorul linie | ||||||||||
|
vectorul coloana |
Fig. 6. Transpusa matricei rara din figura 2.
void MatriceRara::operator !()
for(i=0;i<NrElem-1;i++)
for(int j=i+1;j<NrElem;j++)
}
aux=NrLinii;
NrLinii=NrColoane;
NrColoane=aux;
}
Operatia de adunare a doua matrice rare este realizata prin supraincarcarea operatorului +. Metoda implementeaza parcurgerea o singura data a vectorilor asociati celor doua matrice profitand de faptul ca ambii operanzi sunt obtinuti prin parcurgerea elementelor in ordinea liniilor. Deoarece vectorii sunt alocati dinamic este necesara determinarea numarului de elemente nenule din matricea rara rezultata in urma operatiei de adunare. Astfel se evita repetarea etapei de adaugare a unui element nou la un vector alocat dinamic care se rezuma la stergerea, respectiv, realocarea vectorului pentru a include noua valoare. Adunarea a doua matrice rare se realizeaza in conditiile in care au aceeasi dimensiune.
MatriceRara MatriceRara::operator +(MatriceRara Matrice)
}
MatriceRez.NrElem = NrElem + Matrice.NrElem - NrElemRez_Comune_Nule;
cout<<'n Matricea suma are '<<MatriceRez.NrElem<<' elementen';
if(MatriceRez.NrElem)
else
if (VectLin[i]>Matrice.VectLin[j])
else
if (VectCol[i]<Matrice.VectCol[j])
else
if(VectCol[i]>Matrice.VectCol[j])
else
if (!(VectVal[i]+Matrice.VectVal[j]))
else
if(i==NrElem)
for(;k<MatriceRez.NrElem;k++)
if(j==Matrice.NrElem)
for(;k<MatriceRez.NrElem;k++)
}
}
}
return MatriceRez;
Inmultirea dintre o matrice rara si un vector de dimensiune egala cu numarul de numarul de coloane al matricei este realizata prin intermediul metodei int * InmultireVector( int *, int). Rezultatul operatiei este un vector cu un numar de elemente egal cu numarul de linii al matricei.
int * MatriceRara::InmultireVector(int * Vector, int DimVector)
}
return VectRez;
}
else
return NULL;
}
Inmultirea dintre o matrice rara si o constanta este implementata prin intermediul operatorului *.
void MatriceRara::operator * (int Val)
Inmultirea dintre doua matrice rare este realizata prin intermediul operatorului *, si se realizeaza doar in conditiile egalitatii dintre numarul de coloane a primei matrice si numarul de linii a celeilalte matricei. Evitarea etapei de adaugare element nou la un vector alocat dinamic se realizeaza prin simularea inmultirii pentru a determina numarul de elemente nenule din rezultat.
MatriceRara MatriceRara::operator * (MatriceRara Matrice)
}
}
if(s!=0)
MatriceRez.NrElem++;
}
if(MatriceRez.NrElem)
}
}
if(s!=0)
}
}
return MatriceRez;
Operatiile cu matrice rare ce implica prelucrarea elementelor dintr-o singura matrice impun acordarea unei atentii deosebite elementelor vectorilor VectLin si VectCol pentru a determina cu exactitate elementul cautat.
Conversii de matrice rare
Conversia unui obiect de tip matrice rara la un masiv bidimensional alocat dinamic este realizata de metoda int ** Conversie ( ).
int ** MatriceRara::Conversie()
else
MatRez[i][j]=0;
}
return MatRez;
Metoda parcurge o singura data vectorul VectVal de valori nenule pentru ca acesta a fost creat prin parcurgerea pe linii a matricei initiale si aceeasi abordare este utilizata si pentru a construi noul masiv bidimensional.
Alte conversii de matrice rare, intre diferitele forme utilizate, sunt posibile si au semnificatie in functie de avantajele oferite de reprezentarea respectiva in contextul unui set particular de operatii.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2879
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved