Metoda programarii dinamice

Metoda programarii dinamice

Prezentarea metodei

Metoda programarii dinamice se aplica problemelor de optimizare in care solutia poate fi privita ca rezultatul unui sir de decizii din multimea deciziilor D = D_0i = D_ni.

Fie sistemul S cu multimea starilor X. Presupunem ca trecerea sistemului S dintr-o stare in alta are loc numai in urma unei decizii.

Un vector reprezinta o solutie si un vector reprezinta o politica a sistemului S. Un vector este o solutie partiala si un vector , este o subpolitica a sistemului S. Printre politicile care determina evolutia sistemului S dintr-o stare initiala x₀ intr-o stare finala x_n poate exista o politica care optimizeaza functia obiectiv. Aceasta politica se numeste politica optima si solutia determinata de politica optima se numeste solutie optima.

Principiul optimalitatii are urmatoarea formulare:

Daca este o solutie optima atunci oricare solutie partiala a sa este optima.

Deci programarea dinamica se poate aplica problemelor pentru care optimul total implica optimul partial.

Analiza de luare a deciziilor incepand cu starea initiala x₀, continuand cu starile x₁, x₂, . si terminand cu starea finala x_n se numeste analiza prospectiva. Analiza de luare a deciziilor incepand cu starea finala x_n, continuand cu starile x_n-1, x_n-2, . si terminand cu starea initiala x₀ se numeste analiza retrospectiva.

In analiza prospectiva, daca sistemul S se afla in starea x_i-1 si se ia decizia d_i I D_0i(x_i-1) atunci S trece in starea x_i, i = 1,, n. Aceasta evolutie poate fi descrisa prin relatiile:

x_i = t_0i(x_i-1, d_i), d_i I D_0i(x_i-1), i = 1,,n

Fie u_0i(x_i, d_i) utilitatea trecerii sistemului S de la starea x_i-1, la starea x_i, i = 1,.,n. Utilitatea totala este functia f_0n(u₀₁,.,u_0n) si reprezinta functia obiectiv. Consideram cazul aditiv f_0n(u₀₁,.,u_0n) = u₀₁ u_0n si f_0i(u_{0 n-i+1}, ., u_0n) = u_{0 n-i+1} + f_0i-1(u_{0 n-i+2}, ., u_0n), i=1,.,n, f₀₀(u_{0 n+1}) = 0. Tinand seama de relatiile x_i = t_0i(x_i-1, d_i), i = 1,.,n, obtinem

Consideram problema de optimizare:

unde optimul este determinat in conditiile x_j = t_0j(x_j-1, d_j), d_j ID_0j(x_j-1), j = n-i+1, ., n, i = 1, ., n.

Teorema 4.6

Pentru i = 1, ., n exista relatiile

(4.1)

unde si optimul se determina dupa toate deciziile d_n-i+1 din D_{0 n-i+1}(x_n-i).

Ecuatiile (4.1) se numesc ecuatiile de recurenta ale programarii dinamice in analiza prospectiva.

In analiza retrospectiva, daca sistemul S se afla in starea x_i si se ia decizia d_i I D_ni(x_i) atunci sistemul S trece in starea x_i-1. Aceasta evolutie poate fi descrisa prin relatiile:

x_i-1 = t_ni(x_i, d_i), d_i I D_ni(x_i), i = 1, ., n

Fie u_ni(x_i, d_i) utilitatea trecerii sistemului S de la starea x_i la starea x_i-1. Utilitatea totala este o functie f_nn (u_n1, ., u_nn) si reprezinta functia obiectiv. Consideram cazul aditiv f_nn (u_n1, ., u_nn) = u_n1 + . + u_nn si f_ni(u_n1, ., u_ni) = f_ni-1 (u_n1 + . + u_{n i-1}) + u_ni, i = 1, ., n, f_n0 (u_n0) = 0. Tinand seama de relatiile x_i-1 = t_ni (x_i, d_i), i = 1, ., n, obtinem:

Consideram problema de optimizare:

unde optimul este determinat in conditiile x_j-1 = t_nj (x_j, d_j), d_j I D_nj (x_j), j = 1,.,i; i = 1,.,n

Teorema 4.7

Pentru i=1,.,n exista relatiile

, (4.2)

unde si optimul se ia dupa toti d_i din D_ni(x_i).

Ecuatiile (4.2) se numesc ecuatii de recurenta ale programarii dinamice in analiza retrospectiva.

Observatii

In relatiile de mai sus avem D_0i = D_ni si u_0i (x_i, d_i) = u_ni (x_i, d_i), 1 i n, f_0n = f_nn. S-au facut notatii diferite cu scopul de a pune in evidenta analiza prospectiva respectiv retrospectiva.

Rezolvarea unei probleme cu metoda programarii dinamice consta in urmatoarele :

verificarea valabilitatii principiului de optimalitate;

stabilirea ecuatiilor de recurenta;

rezolvarea ecuatiilor de recurenta.

Probleme rezolvate

Problema PD1

Problema discreta a rucsacului.

O persoana are un rucsac care poate transporta o greutate maxima gr. Persoana are la dispozitie n obiecte nedivizibile (un obiect poate fi pus in rucsac numai in intregime) si se cunoaste pentru fiecare obiect i greutatea g(i) si beneficiul b(i) care se obtine in urma transportului sau la destinatie.Se cere sa se precizeze ce obiecte trebuie sa transporte persoana in asa fel incat beneficiul sa fie maxim. Se va avea in vedere si faptul ca pentru acelasi beneficiu persoana sa transporte o greutate mai mica.

Utilizam metoda retrospectiva (metoda inapoi) a programarii dinamice. Datele problemei sunt urmatoarele:

gr reprezinta greutatea maxima care poate fi transportata de rucsac;

o=(1, , n) reprezinta vectorul obiectelor nedivizibile;

g=(g(1), , g(n)) reprezinta vectorul greutatilor obiectelor;

b=(b(1), , b(n)) reprezinta vectorul beneficiilor obiectelor.

Punerea sau nu a obiectului i in rucsac reprezinta etapa i, i=1, , n. In program folosim si notatiile:

bm(j) reprezinta beneficiul maxim daca se transporta j unitati de greutate j=1, , gr, luand in calcul primele etape;

be(j) reprezinta beneficiul obtinut pentru j unitati de greutate la etapa i;

sm(j) reprezinta multimea obiectelor corespunzatoare beneficiului bm(j)

se(j) reprezinta multimea obiectelor corespunzatoare beneficiului be(j).

Rezulta ca:

bm(g(1))=b(1), sm(g(1))=, bm(j)=0, sm(j)= , jI

bm(j+g(i))=max,

sm(j+g(i))=se(j),

jI, iI

bt reprezinta beneficiul total;

gt reprezinta greutatea totala.

Algoritmul este prezentat in continuare:

PROGRAM PDR;

BEGIN

READ gr, n, (g(i), b(i), i:=1 TO n);

FOR j := 1 TO gr DO

bm(j):=0; sm(j):=

ENDFOR;

bm(g(1)):=b(1); sm(g(1)):=;

FOR i:=2 TO n DO

be:=bm; se:=sm;

IF be(g(i))<b(i)

THEN bm(g(i)):=b(i); sm(g(i)):=;

ENDIF;

FOR j:=1 TO gr-g(i) DO

IF be(j)≠0

THEN IF be(j+g(i))<be(j)+b(i)

THEN bm(j+g(i)):=be(j)+b(i);

sm(j+g(i)):=se(j)

ENDIF

ENDFOR

ENDFOR

bt:=bm(1); gt:=1;

FOR j:=2 TO gr DO

IF bm(j)>bt

THEN bt:=bm(j); gt:=j;

ENDIF;

ENDFOR;

WRITE bt, gt, sm(gt);

END.

Problema PD2

Problema distantei si drumului minim intre oricare doua noduri ale unei retele orientate G = (N, A, b).

Fie digraful G = (N, A) cu N = multimea nodurilor si A = multimea arcelor. Consideram functia valoare b : A R. Aceasta functie poate fi functia lungime sau functia cost. Digraful G = (N, A) pe care s-a definit functia valoare b se numeste retea orientata si se noteaza G = (N, A, b).

Vom nota cu D_ijk un drum, in digraful G = (N, A), de la nodul i la nodul j si cu D_ij = multimea acestor drumuri. Valoarea unui drum D_ijk = (a₁, . , a_q), notata b(D_ijk), este b(D_ijk) = b(a₁) + . + b(a_q). Un drum D_ijp cu valoarea b(D_ijp) = min se numeste drum de valoare minima sau drum minim. Valoarea b(D_ijp) a drumului minim D_ijp se numeste distanta de la nodul i la nodul j si o notam d_ij.

Exista doua probleme cu dificultati privind notiunile de drum minim si distanta. Prima, poate sa nu existe drum de la nodul i la nodul j si a doua, poate exista drum D_ijk cu valoare arbitrar de mica. Prima problema poate fi rezolvata daca consideram b(D_ijp) = si d_ij = . A doua problema provine din posibilitatea existentei circuitelor cu valoare negativa in reteaua orientata G = (N, A, b). De exemplu, reteaua din figura 4.11 contine circuitul D = (2, 3, 4, 2) cu valoarea b(D

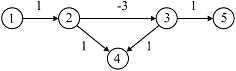
Figura 4.11

Drumurile D_15k , k = 0, 1, ., sunt urmatoarele:

In continuare, vom presupune ca reteaua G = (N, A, b) nu contine circuite cu valoare negativa.

Problema distantei si drumului minim intre oricare doua noduri ale unei retele orientate G = (N, A, b) consta in determinarea unui drum minim D_ijp de la nodul i la nodul j si a distantei d_ij = b(D_ijp) pentru toate nodurile i, j din N, in ipoteza ca reteaua orientata G = (N, A, b) nu contine circuite cu valoare negativa.

Pentru problemele de drum minim intr-o retea orientata G = (N, A, b) principiul optimalitatii este urmatorul:

Daca D_ijp este un drum minim de la nodul i la nodul j, atunci oricare subdrum D_klp al sau este un drum minim de la nodul k la nodul l.

Intr-adevar, daca D_klp nu este drum minim, atunci exista un alt drum D _klp cu valoarea b(D _klp) < b(D_klp). Fie D _ijp = D_ikp D _klp D_ljp. Rezulta b (D _ijp) = b(D_ikp) + b(D _klp) + b(D_ljp) < b(D_ikp) + b(D_klp) + b(D_ljp) = b(D_ijp). Aceasta relatie contrazice faptul ca D_ijp este un drum minim de la nodul i la nodul j. Deci D_klp este drum minim de la nodul k la nodul l.

Conform principiului optimalitatii, drumul minim D_ijp = (i, ., k, ., j) se poate exprima D_ijp = D_ikp D_kjp cu D_ikp, D_kjp drumuri minime de la nodul i la nodul k si respectiv de la nodul k la nodul j. Aceasta exprimare conduce la urmatoarele ecuatii de recurenta:

Aceste ecuatii pot fi rezolvate cu algoritmul Floyd - Warshall.

Consideram reteaua orientata G = (N, A, b) reprezentata prin matricea valoare adiacenta B = (b_ij) _nxn, i, j I N cu

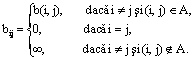
Algoritmul Floyd - Warshall determina matricea distantelor D = (d_ij)_nxn si matricea predecesor P = (p_ij)_nxn.

PROGRAM FLOYD - WARSHALL

BEGIN

FOR i : = 1 TO n DO

FOR j := 1 TO n DO

d_ij := b_ij;

IF i j AND d_ij <

THEN p_iJ := i

ELSE p_ij := 0

ENDIF

ENDFOR;

ENDFOR;

FOR k := 1 TO n DO

FOR i := 1 TO n DO

FOR j := 1 TO n DO

IF d_ik + d_kj < d_ij THEN

d_ij:= d_ik + d_kj; p_ij:= p_kj; END;

ENDIF;

ENDFOR;

ENDFOR;

ENDFOR

END.

Un drum minim D_ijp de la nodul i la nodul j se determina cu algoritmul urmator:

PROGRAM DRUM;

BEGIN

k := n; x_k := j;

WHILE x_k i DO

X_K-1:=;

k := k-1;

ENDWHILE;

END.

Drumul minim este D_ijp = (x_k, x_k+1, ., x_n-1, x_n) = (i, x_k+1, ., x_n-1, j).

Propozitia

Algoritmul Floyd - Warshall determina matricea distantelor D si matricea predecesor P ale retelei orientate G = (N, A, b) cu b : A R si cu proprietatea ca oricare circuit are valoarea b(

Demonstratie

Fie D₀, P₀ matricele definite in liniile de la (3) la (11) si D_k, P_k matricele calculate in liniile de la (12) la (19) la iteratia k. Prin inductie dupa k aratam ca D_k = (d^k_ij) este matricea valorilor drumurilor minime de la i la j avand nodurile interioare din . Pentru k = 0 avem D₀ = B si afirmatia este evident adevarata. Presupunem afirmatia adevarata pentru k-1. Liniile (15), (16) la iteratia k sunt echivalente cu . Din ipoteza inductiva si principiul optimalitatii drumului minim rezulta ca este matricea valorilor drumurilor minime de la i la j avand nodurile interioare din . Deoarece oricare circuit are valoarea b( 0 si in conformitate cu cele precizate mai sus rezulta ca D = D_n este matricea distantelor. De asemenea, din modul cum se determina p_ij rezulta ca P = P_n este matricea predecesor cu ajutorul careia se determina drumurile minime D_ijp.

Propozitia 4.2

Algoritmul Floyd - Warshall are complexitatea O (n³).

Demonstratie

Evident.   

Codul sursa al programului este:

#include<stdio.h>

const int inf=1000;

void AfisMat(int a[20][20], int n)

void FloydWarshall(int n, int b[20][20], int d[20][20], int p[20][20])

for(k=1;k<=n;k++)

for(i=1;i<=n;i++)

for(j=1;j<=n;j++)

if(d[i][k]+d[k][j]<d[i][j])

void drum(int p[20][20], int n, int i, int j)

printf('Drumul de la %d la %d este ',i,j);

for(i=k;i<=n;i++)

printf('%d ',x[i]);

printf('n');

void main()

printf('Numarul de muchii: ');

scanf('%d',&m);

for(i=1;i<=m;i++)

FloydWarshall(n, b, d, p);

printf('Matricea drumurilor: n');

AfisMat(d, n);

printf('Matricea de precedenta: n');

AfisMat(p, n);

printf('Intre ce vf vreti sa vedeti dr minim?n');

printf('i=');

scanf('%d', &i);

printf('j=');

scanf('%d',&j);

drum(p, n, i, j);

Problema PD3

Se da un sir de n matrice A₁, A₂, ., A_n, matricea A_i avand dimensiunile d_i x d_i+1, pentru i = . Se stie ca, pentru a inmulti doua matrice A si B de dimensiuni n * p respectiv, p * r sunt necesare n*p*r inmultiri elementare. Tinand cont ca, inmultirea matricelor este asociativa, dar nu este comutativa, sa se determine modul in care cele n matrice pot fi inmultite astfel incat numarul de inmultiri elementare sa fie minim.

Fie M_ij costul produsului matricelor A_i, ,A_j reprezentand numarul de inmultiri elementare necesare. In mod clar, M_ii = 0 pentru orice i iar M_1n este costul produsului sirului de matrice A₁A_n.

Demonstrarea principiului optimalitatii:

Fiecare mod de parantezare a unei secvente de matrice poate fi reprezentat printr-un arbore binar (infixat), unde frunzele sunt matricele iar nodurile interioare sunt produsele intermediare.

Fie T arborele corespunzator modului optim de parantezare a secventei de matrice A_iA_j. T are un subarbore stang L si un subarbore drept R. L corespunde produsului B A_i A_k, iar R produsului C = A_k+1 A_j unde i k j-1.

Costul corespunzator lui T este:

Cost(T)= Cost(R) + Cost(L) + Cost(B C)

Pentru ca Principiul Optimalitatii sa fie respectat este necesar sa aratam ca L este arborele asociat parantezarii optime a sirului A_i . A_k si R este arborele asociat parantezarii optime a sirului A_k+1 . A_j. Vom face demonstratia pentru L prin reducere la absurd. Daca L nu este optim inseamna ca exista un arbore L' mai bun pentru produsul secventei de matrice A_i . A_k. Cost(L') < Cost(L). Fie T' arborele care il are pe L subarbore stang si pe R subarbore drept.

Cost(T') = Cost(L') + Cost(R) + Cost(B C) < Cost(L) + Cost(R) + Cost(B C) = Cost(T)

Rezulta ca Cost(T') < Cost(T) ceea ce contrazice presupunerea ca T este arborele corespunzator modului optim de parantezare a secventei de matrice A_iA_j. Prin urmare, L este arborele asociat parantezarii optime a sirului A_i . A_k.

Deducerea formulei de recurenta:

M_ij = Cost(T) = Cost(L) + Cost(R) + Cost(B C

=M_ik + M_k+1,j + d_id_k+1d_j+1.

Intrucat valoare lui k nu este cunoscuta si M_ij se doreste a fi minimul posibil, relatia devine:

M_ij = min

Exemplu

Fie matricele: A₁ (3x5), A₂ (5x7), A₃ (7x3) si A₄ (3x4). Intre paranteze sunt specificate dimensiunile fiecarei matrice. Prin urmare, d₁ = 3, d₂ = 5, d₃ = 7, d₄ = 3, d₅ = 4.

Valorile M_ij se calculeaza dupa cum urmeaza:

Pentru fiecare M_ij este pastrat k-ul pentru care valoarea lui M_ij este minima.

Parantezarea optima este: (A1(A2 A3))A4.

Algoritmul care calculeaza costul minim al produsului sirului de matrice A₁,,A_n este prezentat in pseudocod mai jos. In triunghiul superior sunt pastrate costurile iar in triunghiul inferior k-urile pentru care se obtin valorile minime. Daca M_ij este costul minim atunci M_ji este k-ul pentru care s-a obtinut M_ij-ul.

PROGRAM NR_INMULTIRI

BEGIN

FOR i : = 1 TO n DO A_ii = 0;

FOR l : = 1 TO n-1 DO

FOR i := 1 TO n-1 DO

j := i+l;

a[i,j] :=

FOR k := i to j-1 DO

m := a_i,k + a_k+1,j + dim_i * dim_k+1 * d_j+1;

IF a_i,j > m THEN

a_i,j := m;

a_j,i := k;

ENDIF;

ENDFOR;

ENDFOR;

ENDFOR;

RETURN a_1,n;

END.

Pornind de la informatiile pastrate in matricea M se poatea afisa parantezarea optima a sirului de matrice A₁,.A_n.

SUBPROGRAM PARANTEZARE(i, j

BEGIN

IF i = j THEN

WRITE 'A',i

ELSE

WRITE '(';

PARANTEZARE(i, M_ji

WRITE '*';

PARANTEZARE(M_ji + 1, j

WRITE ')';

END;

ENDIF;

END.

Textul sursa al programului este:

#include<stdio.h>

#include<limits.h>

void nr_inmultiri(int m[100][100], int d[100], int n)

}

}

printf('nr minim de inm: %d', m[1][n]);

void parantezare(int m[100][100], int i, int j)

void main()

nr_inmultiri(m, d, n);

parantezare(m,1,n);

Problema PD4

Se dau doua siruri de numere intregi de m respectiv n elemente. Sa se determine cel mai lung subsir comun al celor doua siruri.

Fiind dat un sir x₁, x₂.x_m, un subsir este un sir z₁, . z_k pentru care exista sirul de indici i₁ < . < i_k astfel incat j < k. Problema cere gasirea celui mai lung subsir comun a doua siruri x₁, x₂.x_m si y₁, y₂.y_n.

Exemplu

Pentru sirurile:

X=(1,6,5,2,3,6,6,2,9,4,10,1,3,8,5,1,9,7)

Y=(6,1,5,6,5,5,4,3,4,5,2,4)

o solutie posibila este: Z=(1,5,6,4,3,5)

Fie X_k x₁ x₂ x_k) prefixul lui X de lungime k si Y_h y₁ y₂ y_h) prefixul lui Y de lungime h. Notam cu L(X_k,Y_h) lungimea celui mai lung subsir comun al lui X_k Y_h

Ca si la problema precedenta vom utiliza o matrice L in care L_ij va fi lungimea celui mai lung subsir comun al sirurilor X_i si Y_j.

Relatia de recurenta care va sta la baza constructiei matricei este:

L_i0 = 0 i =

L_0j = 0 j =

Daca X_k+1 = Y_h+1 atunci L(X_k+1,Y_h+1) = 1 + L(X_k,Y_h).

Daca X_k+1 ≠ Y_h+1 atunci L(X_k+1,Y_h+1) = max(L(X_k,Y_h+1), L(X_k+1,Y_h)).

Algoritmul in pseudocod care descrie formulele de mai sus este:

PROGRAM SUBSIR

BEGIN

FOR i : = 1 TO n DO L_i0 = 0;

FOR j : = 1 TO m DO L_0j = 0;

FOR i : = 1 TO n DO

FOR j := 1 TO m DO

IF X_i = Y_j THEN

L_ij = 1 + L_i-1,j-1;

ELSE

IF L_i-1,j > L_i,j-1 THEN

L_i,j = L_i-1,j

ELSE

L_i,j = L_i,j-1

ENDIF;

ENDIF;

ENDFOR;

ENDFOR;

END.

Afisarea subsirului comun obtinut se face prin:

SUBPROGRAM AFISARE

BEGIN

i = n; j = m; k = 1;

WHILE L_ij <> 0 DO

IF X_i = Y_j THEN

Z_k = X_i;

i = i - 1; j = j - 1; k = k + 1;

ELSE

IF L_i-1,j > L_i,j-1 THEN

i = i - 1;

ELSE

j = j - 1;

ENDIF;

ENDIF;

ENDWHILE;

WRITE Z;

END.

Textul sursa al programului este:

#include<stdio.h>

void afisare(int a[20], int n)

void subsir(int a[20][20], int x[20],int y[20],int n,int m)

void afisare_subsir(int a[20][20], int x[20], int y[20], int n, int m)

else

if(a[i][j]==a[i-1][j])

i--;

else

j--;

printf('Sirul comun de lungime maxima este: ');

for(i=k;i>=1;i--)

printf('%d ',z[i]);

printf('n');

void main()

printf('m=');

scanf('%d',&m);

for(i=1;i<=m;i++)

printf('Primul sir: ');

afisare(x,n);

printf('Al doilea sir: ');

afisare(y,m);

subsir(a, x, y, n, m);

afisare_subsir(a, x, y, n, m);