| CATEGORII DOCUMENTE |
structuri de Graf
1 Grafuri ca structuri de date
Operatiile cu grafuri pot fi considerate:
- Ca un capitol de matematica (teoria grafurilor a fost dezvoltata de matematicieni);
- Ca o sursa de algoritmi nebanali, ilustrand diferite clase de algoritmi, solutii alternative pentru o aceeasi problema si metode de analiza a complexitatii lor;
- Ca probleme de programare ce folosesc diverse structuri de date.
Aici ne intereseaza acest ultim aspect - probleme de grafuri ca studii de caz in folosirea unor structuri de date, cu implicatii asupra performantelor aplicatiilor, mai ales ca unele probleme practice cu grafuri au dimensiuni foarte mari.
Graful este un model abstract (matematic) pentru multe probleme reale, concrete, a caror rezolvare necesita folosirea unui calculator. In matematica un graf este definit ca o pereche de doua multimi G = (V,M), unde V este multimea (nevida) a varfurilor (nodurilor), iar M este multimea muchiilor (arcelor). O muchie din M uneste o pereche de doua varfuri din V si se noteaza cu (v,w).
De obicei nodurile unui graf se numeroteaza incepand cu 1 si deci multimea V este o submultime a multimii numerelor naturale N.
Termenii "varf" si "muchie" provin din analogia unui graf cu un poliedru si se folosesc mai ales pentru grafuri neorientate. termenii "nod" si "arc" se folosesc mai ales pentru grafuri orientate.
Intr-un graf orientat, numit si digraf, arcul (v,w) pleaca din nodul v si intra in nodul w; el este diferit de arcul (w,v) care pleaca de la w la v. Intr-un graf neorientat poate exista o singura muchie intre doua varfuri date, notata (v,w) sau (w,v).
Deoarece in multimea M nu pot exista elemente identice inseamna ca intre doua noduri dintr-un graf orientat pot exista cel mult doua arce, iar intre doua varfuri ale un graf neorientat poate exista cel mult o muchie. Doua noduri intre care exista un arc se numesc si noduri vecine sau adiacente. Intr-un graf orientat putem vorbi de succesorii si de predecesorii unui nod, respectiv de arce care ies si de arce care intra intr-un nod.
Un drum (o cale) intr-un graf uneste o serie de noduri v[1], v[2],v[n] printr-o secventa de arce (v[1],v[2]), (v[2],v[3]),Intre doua noduri date poate sa nu existe un arc, dar sa existe o cale, ce trece prin alte noduri intermediare.
Un graf este conex daca, pentru orice pereche de noduri (v,w) exista cel putin o cale de la v la w sau de la w la v.
Un digraf este tare conex (puternic conectat) daca, pentru orice pereche de noduri (v,w) exista (cel putin) o cale de la v la w si (cel putin) o cale de la w la v. Un exemplu de graf tare conex este un graf care contine un ciclu care trece prin toate nodurile: (1,2), (2,3), (3,4), (4,1).
O componenta conexa a unui graf (V,M) este un subgraf conex (V',M') unde V' este o submultime a lui V, iar M' este o submultime a lui M. Impartirea unui graf neorientat in componente conexe este unica, dar un graf orientat poate fi partitionat in mai multe moduri in componente conexe. De exemplu, graful (1,2),(1,4),(3,2),(3,4) poate avea componentele conexe si sau si .
Un ciclu in graf (un circuit) este o cale care porneste si se termina in acelasi nod. Un ciclu hamiltonian este un ciclu complet, care uneste toate nodurile dintr-un graf.
Un graf neorientat conex este ciclic daca numarul de muchii este mai mare sau egal cu numarul de varfuri.
Un arbore liber este un graf conex fara cicluri si poate fi neorientat sau orientat.
Putem deosebi trei categorii de grafuri:
a) Grafuri de relatie (simple), in care se modeleaza doar relatiile dintre entitati, iar arcele nu au alte atribute.
b) Grafuri cu costuri (retele), in care fiecare arc are un cost asociat (o distanta geometrica, un timp de parcurgere, un cost exprimat in bani). Intre costurile arcelor nu exista nici o relatie.
c) Retele de transport, in care fluxul (debitul) prin fiecare arc (tronson de retea) este corelat cu fluxul prin arcele care vin sau pleaca din acelasi nod.
Anumite probleme reale sugereaza in mod natural modelarea lor prin grafuri: probleme asociate unor retele de comunicatie, unor retele de transport de persoane sau de marfuri, retele de alimentare cu apa, cu energie electrica sau termica, s.a.
Alteori asocierea obiectelor din lumea reala cu nodurile si arcele unui graf este mai putin evidenta. Arcele pot corespund unor relatii dintre persoane ( persoana x cunoaste persoana y) sau dintre obiecte (piesa x contine piesa y) sau unor relatii de conditionare ( operatia x trebuie precedata de operatia y).
Un graf poate fi privit si ca o structura de date abstracta, care permite orice relatii intre componentele structurii. Operatiile uzuale asociate structurii de graf sunt:
- Initializare graf cu numar dat de noduri: initG (Graph & g,int n);
- Adaugare muchie (arc) la un graf: addArc (Graph & g, int x, int y);
- Verifica existenta unui arc de la un nod x la un nod y: int arc(Graph g,int x,int y);
- Eliminare arc dintr-un graf : delArc (Graph & g, int x, int y);
- Eliminare nod dintr-un graf : delNod (Graph & g, int x);
Mai multi algoritmi pe grafuri necesita parcurgerea vecinilor (succesorilor) unui nod dat, care poate folosi functia "arc" intr-un ciclu repetat pentru toti vecinii posibili (deci pentru toate nodurile din graf). Pentru grafuri reprezentate prin liste de vecini este suficienta parcurgerea listei de vecini a unui nod, mult mai mica decat numarul de noduri din graf (egala cu numarul de arce asociate acelui nod).
De aceea se considera uneori ca operatii elementare cu grafuri urmatoarele:
- Pozitionare pe primul succesor al unui nod dat ('firstSucc');
- Pozitionare pe urmatorul succesor al unui nod dat ('nextSucc').
Exemplu de afisare a succesorilor unui nod dat k dintr-un graf g:
p=firstSucc(g,k); // p= adresa primului succesor
if (p !=NULL)
Pentru un graf cu costuri (numit si "retea") apar cateva mici diferente la functiile "arc" (costul unui arc) si "addArc" (mai are un argument care este costul arcului) :
typedef struct Net;
void addArc (Net & g, int v,int w,int cost)
int arc (Net & g, int v, int w)
2 Reprezentarea grafurilor prin alte structuri
Reprezentarea cea mai directa a unui graf este printr-o matrice de adiacente (de vecinatati), pentru grafuri de relatie respectiv printr-o matrice de costuri, pentru retele. Avantajele reprezentarii unui graf printr-o matrice sunt:
- Simplitatea si claritatea programelor.
- Aceeasi reprezentare pentru grafuri orientate si neorientate, cu sau fara costuri.
- Se pot obtine usor si repede succesorii sau predecesorii unui nod dat v (coloanele nenule din linia v sunt succesorii, iar liniile nenule din coloana v sunt predecesorii).
- Timp constant pentru verificarea existentei unui arc intre doua noduri date (nu necesita cautare, deci nu depinde de dimensiunea grafului).
Reprezentarea matriciala este preferata in determinarea drumurilor dintre oricare doua varfuri (tot sub forma de matrice), in determinarea drumurilor minime dintre oricare doua varfuri dintr-un graf cu costuri, in determinarea componentelor conexe ale unui graf orientat (prin transpunerea matricei se obtine graful cu arce inversate, numit si graf dual al grafului initial), si in alte aplicatii cu grafuri.
O matrice este o reprezentare naturala pentru o colectie de puncte cu atribute diferite: un labirint (puncte accesibile si puncte inaccesibile), o suprafata cu puncte de diferite inaltimi, o imagine formata din puncte albe si negre (sau colorate diferit), s.a.
Dezavantajul matricei de adiacente apare atunci cand numarul de noduri din graf este mult mai mare ca numarul de arce, iar matricea este rara ( cu peste jumatate din elemente nule). In astfel de cazuri se prefera reprezentarea prin liste de adiacente.
Matricea de adiacente 'a' este o matrice patratica cu valori intregi , avand numarul de linii si de coloane egal cu numarul de noduri din graf. Elementele a[i][j] sunt:
1 (true) daca exista arc de la i la j sau 0 (false) daca nu exista arc de la i la j
Exemplu de definire a unui tip graf printr-o matrice de adiacente alocata dinamic:
// cu matrice alocata dinamic
typedef struct Graf ;
In general numarul de noduri dintr-un graf poate fi cunoscut de program inca de la inceput si matricea de adiacente poate fi alocata dinamic.
Matricea de adiacente pentru graful (1,2),(1,4),(3,2),(3,4) este:
1 2 3 4
1 0 1 0 1 linia 0 si coloana 0 nefolosite !
2 0 0 0 0
3 0 1 0 1
4 0 0 0 0
Succesorii unui nod dat v sunt elementele nenule din linia v , iar predecesorii unui nod v sunt elementele nenule din coloana v. De obicei nu exista arce de la un nod la el insusi si deci a[i][i]=0.
Exemple de functii cu grafuri in cazul utilizarii matricei de adiacente.
void initG (Graf & g, int n)
void addArc (Graf & g, int x,int y)
int arc (Graf & g, int x, int y)
void delArc (Graf& g,int x,int y)
}
Eliminarea unui nod din graf ar trebui sa modifice si dimensiunile matricei, dar vom elimina doar arcele ce pleaca si vin in acel nod:
void delNode (Graf & g, int x)
Pentru un graf cu costuri vom inlocui functia "arc" cu o functie "carc" care are ca rezultat costul unui arc, iar acolo unde nu exista arc vom pune o valoare foarte mare (mai mare ca orice cost din graf), care corespunde unui cost infinit.
typedef struct Net; // retea (graf cu costuri)
void addArc (Net & g, int v,int w,int cost)
void delArc (Net& g,int v, int w)
int arc (Net & g, int v, int w)
Vom aborda acum reprezentarea grafurilor printr-un vector de pointeri la liste de noduri vecine (liste de adiacente).
Lista tuturor arcelor din graf este impartita in mai multe subliste, cate una pentru fiecare nod din graf. Listele de noduri vecine pot avea lungimi foarte diferite si de aceea se prefera implementarea lor prin liste inlantuite. Reunirea listelor de succesori se poate face de obicei intr-un vector, deoarece permite accesul direct la un nod pe baza numarului sau (fara cautare). Figura urmatoare arata cum se poate reprezenta graful (1,2),(1,4),(3,2),(3,4) printr-un vector de pointeri la liste de adiacente.
__ ______ ______
1 |__ |----->|_2_|_x_|--->|_4_|_x_|
2 |_x | _______ ______
3 |__ |----->|_2_|_x_|--->|_4_|_x_|
4 |_x |
Ordinea nodurilor intr-o lista de adiacente nu este importanta si de aceea putem adauga mereu la inceputul listei de noduri vecine.
Exemple de operatii elementare cu grafuri in cazul folosirii listelor de adiacente:
typedef struct nod * pnod ; // ptr este un tip pointer
typedef struct Graf;
void initG (Graf & g, int n)
void addArc (Graf & g, int x, int y)
int arc (Graf g,int x,int y)
Reprezentarea unui graf prin liste de vecini ai fiecarui varf asigura cel mai bun timp de explorare a grafurilor (timp proprtional cu suma dintre numarul de varfuri si numarul de muchii din graf), iar explorarea apare ca operatie in mai multi algoritmi pe grafuri.
Pentru un graf neorientat fiecare muchie (x,y) este memorata de doua ori: y in lista de vecini a lui x si x in lista de vecini a lui y.
Pentru un graf orientat listele de adiacente sunt de obicei liste de succesori, dar pentru unele aplicatii intereseaza predecesorii unui nod (de ex. in sortarea topologica). Lipsa de simetrie poate fi un dezavantaj al listelor de adiacente pentru reprezentarea grafurilor orientate.
Pe langa reprezentarile principale ale structurilor de graf (matrice si liste de adiacente) se mai folosesc uneori si alte reprezentari:
- O lista de arce (de perechi de noduri) este utila in anumiti algoritmi (cum este algoritmul lui Kruskal), dar mareste timpul de cautare: timpul de executie al functiei 'arc' creste liniar cu numarul de arce din graf.
- O matrice de biti este o reprezentare mai compacta a unor grafuri de relatie cu un numar foarte mare de noduri.
- Un vector de pointeri la vectori (cu vectori in locul listelor de adiacente) necesita mai putina memorie si este potrivit pentru un graf static, care nu se mai modifica.
- Pentru grafuri planare care reprezinta puncte si distante pe o harta poate fi preferabila o reprezentare geometrica, printr-un vector cu coordonatele varfurilor.
Anumite cazuri particulare de grafuri pot fi reprezentate mai simplu.
Un arbore liber este un graf neorientat aciclic; intr-un arbore liber nu exista un nod special radacina. Intr-un arbore fiecare varf are un singur parinte (predecesor), deci am putea reprezenta arborele printr-un vector de noduri parinte.
Rezultatul mai multor algoritmi este un arbore liber si acesta se poate reprezenta compact printr-un singur vector. Exemple: arbori de acoperire de cost minim, arborele cu drumurile minime de la un punct la toate celelalte (Dijkstra), s.a.
Un graf conex se poate reprezenta printr-o singura lista - lista arcelor, iar numarul de noduri este valoarea maxima a unui nod prezent in lista de arce (toate nodurile din graf apar in lista de arce). Lista arcelor poate fi un vector sau o lista de structuri, sau doi vectori de noduri:
typedef struct arc; // un arc
typedef arc graf[M] ; // lista de arce
Figura urmatoare arata un arbore liber si lista lui de arce.
1 o o 5 __1_____2____3____4____5___
/ x |__1__|__2__|__3__|__4__|__4__|
3 o----o 4 y |__3__|__3__|__4__|__5__|__6__|
/
2 o o 6
Pentru arbori liberi aceasta reprezentare poate fi simplificata si mai mult, daca vom impune ca pozitia in vector sa fie egala cu unul dintre noduri. Vom folosi deci un singur vector P, in care P[k] este perechea (predecesorul) nodului k. Este posibil intotdeauna sa notam arcele din arbore astfel incat fiecare nod sa aiba un singur predecesor (sau un singur succesor).
Pentru arborele anterior vectorul P va fi:
__1_____2____3_____4____5____6__
P |_____|__3__|__1__|__3__|__4__|__4__|
Lista arcelor (k,P[k]) este deci: (2,3),(3,1),(4,3),(5,4),(6,4).
Am considerat ca nodul 1 nu are nici un predecesor, dar putem sa consideram ca nodul ultim nu are nici un predecesor:
__1_____2____3_____4____5__
P |__3__|__3__|__4__|__6__|__4__|
Un astfel de vector este chiar vectorul solutie intr-o abordare backtracking a unor probleme de grafuri.
3 Metode de explorare a grafurilor
Pentru a ilustra utilizarea tipului abstract "graf" intr-o problema tipica de grafuri vom prezenta aici doi algoritmi de explorare a grafurilor.
Explorarea unui graf inseamna vizitarea sistematica a tuturor nodurilor din graf, folosind arcele existente, astfel incat sa se treaca o singura data prin fiecare nod.
Rezultatul explorarii unui graf este o colectie de arbori de explorare , numita si 'padure' de acoperire. Daca se pot atinge toate nodurile unui graf pornind dintr-un singur nod, atunci rezulta un singur arbore de acoperire. Explorarea unui graf neorientat conex conduce la un singur arbore, indiferent care este nodul de pornire.
Rezultatul explorarii unui graf orientat depinde mult de nodul de plecare. Pentru graful orientat cu arcele (1,4),(2,1),(3,2),(3,4),(4,2) numai vizitarea din nodul 3 poate atinge toate celelalte noduri.
De obicei se scrie o functie care primeste un nod de start si incearca sa atinga cat mai multe noduri din graf. Aceasta functie poate fi apelata in mod repetat, pentru fiecare nod din graf considerat ca nod de start. Astfel se asigura vizitarea tuturor nodurilor pentru orice graf. Fiecare apel genereaza un arbore de acoperire a unei submultimi de noduri.
Explorarea unui graf poate fi vazuta si ca o metoda de enumerare a tuturor nodurilor unui graf, sau ca o metoda de cautare a unui drum catre un nod dat din graf.
Transformarea unui graf (structura bidimensionala) intr-un vector (structura liniara) se poate face in multe feluri, deoarece fiecare nod are mai multi succesori si trebuie sa alegem numai unul singur pentru continuarea explorarii.
Algoritmii de explorare dintr-un nod dat pot folosi doua metode:
- Explorare in adancime (DFS = Depth First Search)
- Explorare in largime (BFS = Breadth First Search)
Explorarea in adancime foloseste, la fiecare nod, un singur arc, care conduce la un alt nod si astfel se patrunde cat mai repede in adancimea grafului. Daca raman noduri nevizitate, se revine treptat la nodurile deja vizitate pentru a lua in considerare si alte arce, ignorate in prima faza. Explorarea DF din nodul 3 a grafului anterior produce secventa de noduri 3,2,1,4 iar arborele de acoperire este format din arcele 3-2, 2-1 si 1-4. Sunt posibile si alte secvente de vizitare DF pentru acelasi graf, daca nu se alege succesorul cu numar minim pentru inaintare: 3-2, 2-4, 2-1 sau 3-4, 3-2, 2-1 , s.a.
Explorarea in largime foloseste, la fiecare nod, toate arcele care pleaca din nodul respectiv si dupa aceea trece la alte noduri (la succesorii nodurilor vizitate). In felul acesta se exploreaza mai intai nodurile adiacente, din 'latimea' grafului si apoi se coboara mai adanc in graf. Explorarea BF din nodul 3 a grafului anterior conduce la secventa de noduri 3,2,4,1 si la arborele de acoperire 3-2, 3-4, 2-1 , daca se folosesc succesorii in ordinea crescatoare a numerelor lor.
Este posibil ca pentru grafuri diferite sa rezulte o aceeasi secventa de noduri, dar lista de arce este unica pentru fiecare graf (daca se aplica acelasi algoritm).
De asemenea este posibil ca pentru anumite grafuri sa rezulte acelasi arbore de acoperire atat la explorarea DF cat si la explorarea BF.
Vizitarea DF a unui graf aciclic corespunde vizitarii prefixate de la arbori binari.
Algoritmul de explorare DFS poate fi exprimat recursiv sau iterativ, folosind o stiva de noduri. Ambele variante trebuie sa tina evidenta nodurilor vizitate pana la un moment dat, pentru a evita vizitarea repetata a unor noduri. Cea mai simpla implementare a multimii de noduri vizitate este un vector 'vazut', initializat cu zerouri si actualizat dupa vizitarea fiecarui nod x (vazut[x]=1).
Exemplul urmator contine o procedura recursiva de explorare DF dintr-un nod dat v si un program principal pentru vizitarea tuturor nodurilor.
int vazut[100]=; // ptr marcare noduri vizitate
void dfs (Graf g,int v)
// afisare arbori de explorare graf
void main ()
}
Pentru afisarea de arce in loc de noduri se modifica putin functia, dar ea nu va afisa nimic daca nu se poate atinge nici un alt nod din nodul de plecare. Este posibil ca un arbore de explorare sa contina un singur nod si nici un arc.
Un algoritm DFS nerecursiv trebuie sa foloseasca o stiva pentru a memora succesorii (vecinii) neprelucrati ai fiecarui nod vizitat, astfel ca sa putem reveni ulterior la ei. Algoritmul DFS nerecursiv poate fi descris astfel:
pune nodul de plecare in stiva
repeta cat timp stiva nu e goala
scoate din stiva in x
afisare si marcare x
pune in stiva orice succesor nevizitat y al lui x
Pentru ca functia DFS nerecursiva sa produca aceleasi rezultate ca si functia DFS recursiva, succesorii unui nod sunt pusi in stiva in ordinea descrescatoare a numerelor lor (extragerea lor din stiva si afisarea lor se va face in ordine inversa).
// explorare DFS nerecursiva
void dfs (Graf g,int v)
}
}
Evolutia stivei si variabilelor x,y pentru graful (1,2)(1,4),(2,3),(2,4),(3,4) va fi:
stiva s x y afisare
- 1 1
- 1 4
4 1 2
4 2 2
4 2 4
4,4 3 3
4,4 3 4
4,4 4 4
Algoritmul de explorare in largime afiseaza si memoreaza pe rand succesorii fiecarui nod. Ordinea de prelucrare a nodurilor memorate este aceeasi cu ordinea de introducere in lista, deci lista este de tip "coada". Algoritmul BFS este foarte asemanator algoritmului DFS nerecursiv, diferenta apare numai la tipul listei folosite pentru memorarea temporara a succesorilor fiecarui nod: stiva la DFS si coada la BFS
// explorare in largime dintr-un nod dat v
void bfs ( Graf g, int v, int vazut[])
}
}
Evolutia cozii q si a variabilelor x,y la explorarea BF a grafului cu arcele (1,2),(1,4),(2,3),(2,4),(3,4):
coada q x y afisare
1 2 1 - 2
Un drum minim intre doua varfuri este drumul care foloseste cel mai mic numar de muchii. Drumurile minime de la un varf v la toate celelalte noduri pot fi gasite prin explorare in largime din nodul v, cu actualizare distante fata de v, la fiecare coborare cu un nivel in graf. Vom folosi un vector d cu d[y]=distanta varfului y fata de 'radacina' v si un vector p, cu p[y]=numar varf predecesor pe calea de la v la y.
// distante minime de la v la toate celelalte noduri din g
void bfs (Graph g, int v,int vazut[],int d[], int p[])
Pentru afisarea varfurilor de pe un drum minim de la v la x trebuie parcurs in sens invers vectorul p (de la ultimul element la primul):
x p[x] p[p[x]] . v
4 Sortare topologica
Problema sortarii topologice poate fi formulata astfel: intre elementele unei multimi A exista relatii de conditionare (de precedenta ) de forma a[i] << a[j], exprimate in cuvinte astfel: a[i] precede (conditioneaza) pe a[j], sau a[j] este conditionat de a[i]. Se mai spune ca a[i] este un predecesor al lui a[j] sau ca a[j] este un succesor al lui a[i]. Un element poate avea oricati succesori si predecesori. Multimea A supusa unor relatii de precedenta poate fi vazuta ca un graf orientat, avand ca noduri elementele a[i] ; un arc de la a[i] la a[j] arata ca a[i] precede pe a[j].
Exemplu : A =
2 << 1 1 << 3 2 << 3 2 << 4 4 << 3 3 << 5 4 << 5
Scopul sortarii topologice este ordonarea (afisarea) elementelor multimii A intr-o succesiune liniara astfel incat fiecare element sa fie precedat in aceasta succesiune de elementele care il conditioneaza.
Elementele multimii A pot fi privite ca noduri dintr-un graf orientat, iar relatiile de conditionare ca arce in acest graf. Sortarea topologica a nodurilor unui graf orientat nu este posibila daca graful contine cel putin un ciclu. Daca nu exista nici un element fara conditionari atunci sortarea nici nu poate incepe. Uneori este posibila numai o sortare topologica partiala, pentru o parte din noduri.
Pentru exemplul dat exista doua secvente posibile care satisfac conditiile de precedenta :
2, 1, 4, 3, 5 si 2, 4, 1, 3, 5
Determinarea unei solutii de ordonare topologica se poate face in cateva moduri:
a) Incepand cu elementele fara predecesori (neconditionate) si continuand cu elementele care depind de acestea (nodul 2 este un astfel de element in exemplul dat);
b) Incepand cu elementele fara succesori (finale) si mergand catre predecesori, din aproape in aproape ( nodul 5 in exemplu).
c) Algoritmul de explorare in adancime a unui graf orientat, completat cu afisarea nodului din care incepe explorarea, dupa ce s-au explorat toate celelalte noduri.
Aceste metode poate folosi diferite structuri de date pentru reprezentarea relatiilor dintre elemente; in cazul b) trebuie sa putem gasi usor succesorii unui element, in cazul a) trebuie sa putem gasi usor predecesorii unui element.
Algoritmul de sortare topologica cu liste de predecesori este:
repeta
cauta un nod nemarcat si fara predecesori
daca s-a gasit atunci
afiseaza nod si marcheaza nod
sterge nod marcat din graf
pana cand nu mai sunt noduri fara predecesori
daca raman noduri nemarcate atunci
nu este posibila sortarea topologica
Pentru exemplul dat evolutia listelor de predecesori este urmatoarea:
scrie 2 scrie 1 scrie 4 scrie 3 scrie 5
Programul urmator ilustreaza acest algoritm .
// determina nr de conditionari nod v
int nrcond (Graf g, int v )
// sortare topologica si afisare
void topsort (Graf g) {
int i,j,n=g.n,ns,gasit, sortat[50]=;
ns=0; // noduri sortate si afisate
do
} while (gasit);
if (ns != n) printf ('n nu este posibila sortarea topologica! ');
Algoritmul de sortare topologica cu liste de succesori este:
repeta
cauta un nod fara succesori
pune nod gasit in stiva si marcheaza ca sortat
elimina nod marcat din graf
pana cand nu mai exista noduri fara succesori
daca nu mai sunt noduri nemarcate atunci
repeta
scoate nod din stiva si afisare nod
pana cand stiva goala
Evolutia listelor de succesori pentru exemplul dat este:
pune 5 pune 3 pune 1 pune 4 pune 2
La extragerea din stiva se afiseaza: 2, 4, 1, 3, 5
5 Aplicatii ale explorarii in adancime
Explorarea in adancime sta la baza altor algoritmi cu grafuri, cum ar fi: determinarea existentei ciclurilor intr-un graf, gasirea componentelor puternic conectate dintr-un graf, sortare topologica, determinare puncte de articulare s.a.
Determinarea componentelor conexe ale unui graf se poate face prin repetarea explorarii DF din fiecare nod nevizitat in explorarile anterioare. Un apel al functiei "dfs" afiseaza o componenta conexa. Pentru grafuri neorientate exista un algoritm mai performant de aflare a componentelor conexe, care foloseste tipul abstract de date "colectie de multimi disjuncte".
Algoritmul de sortare topologica derivat din explorarea DF se bazeaza pe faptul ca explorarea in adancime viziteaza toti succesorii unui nod. Explorarea DF va fi repetata pana cand se viziteaza toate nodurile din graf. Functia "tops" este derivata din functia 'dfs', in care s-a inlocuit afisarea cu punerea intr-o stiva a nodului cu care a inceput explorarea, dupa ce s-au memorat in stiva succesorii sai. In final se scoate din stiva si se afiseaza tot ce a pus functia "tops".
Programul urmator realizeaza sortarea topologica ca o varianta de explorare in adancime a unui graf g si foloseste o stiva s pentru memorarea nodurilor.
Stack s; // stiva folosita in doua functii
// sortare topologica dintr-un nod v
void tops (Graf g,int v)
// sortare topologica graf
void main ()
Secventa de apeluri si evolutia stivei pentru exemplul dat :
v Stiva Apel
1 din main
3 din tops
5 din tops
2 din main
4 din tops
Numerotarea nodurilor in ordinea de vizitare DF permite clasificarea arcelor unui graf orientat in patru clase:
- Arce de arbore, componente ale arborilor de explorare in adancime (de la un nod in curs de vizitare la un nod nevizitat inca).
- Arce de inaintare, la un succesor (la un nod cu numar de vizitare mai mare).
- Arce de revenire, la un predecesor (la un nod cu numar de vizitare mai mic).
- Arce de traversare, la un nod care nu este nici succesor, nici predecesor .

![]() 3
3
Fie graful cu 4 noduri si 6 arce:
Dupa explorarea DF cele 6 arce se impart in:
Arce de arbore (dfs): (1,2), (2,3), (2,4)
Arce inainte : (1,3)
Arce inapoi : (4,1)
Arce transversale : (4,3)
Numerele de vizitare DF pentru nodurile 1,2,3,4 sunt: 1,2,3,4 iar vectorul P contine numerele 0,1,2,2 (in 3 si 4 se ajunge din 2).
Daca exista cel putin un arc de revenire la explorarea DF a unui graf orientat atunci graful contine cel putin un ciclu, iar un graf orientat fara arce de revenire este aciclic.
Pentru a diferentia arcele de revenire de arcele de traversare se memoreaza intr-un vector P nodurile din arborele de explorare DF; un arc de revenire merge catre un nod din P, dar un arc de traversare nu are ca destinatie un nod din P.
// clasificare arce la explorare in adancime dintr-un nod dat v
void dfs (int v, int t[ ])
else // daca w este deja vizitat
if ( nv[v] < nv[w]) // daca w vizitat dupa v
t[k]='I'; // atunci v-w este arc inainte
else // daca w vizitat inaintea lui v
if ( precede(w,v) ) // daca w precede pe v in arborele DFS
t[k]='R'; // atunci v-w este arc inapoi (de revenire)
else // daca w nu precede pe v in arborele DFS
t[k]='T'; // atunci v=w este arc transversal
// daca v precede pe w in arborele DFS
int precede (int v, int w)
Functia de explorare DF poate fi completata cu numerotarea nodurilor atat la primul contact cu nodul, cat si la ultimul contact (la iesirea din functia dfs). Functia dfs care urmeaza foloseste variabila externa: variabila 't' este initializata cu zero in programul principal si incrementata la fiecare intrare in functia 'dfs'. Vectorul t1 este actualizat la intrarea in functia dfs, iar vectorul t2 la iesirea din dfs. La intrarea in dfs(v) se face t1[v]=t, iar la iesire se face t2[v]=t.
int t; // var externa, implicit zero
void dfs (Graph g, int v, int t1[ ], int t2[ ])
Pentru digraful cu 4 noduri si cu arcele (1,3), (1,4), (2,1), (2,3), (3,4), (4,2) arborele dfs este secventa 1->3->4->2 , iar vectorii t1 si t2 vor contine urmatoarele valori dupa apelul dfs(1) :
nod k 1 2 3 4
t1[k] 1 4 2 3 (intrare in nod)
t2[k] 8 5 7 6 (iesire din nod)
Se observa ca ultimul nod vizitat (2) este si primul parasit, dupa care este parasit nodul vizitat anterior;numerele t1(k) si t2(k) pot fi privite ca paranteze in jurul nodului k, iar structura de paranteze a grafului la vizitare dfs este :
O componenta puternic conectata (tare conexa) dintr-un digraf este o submultime maximala a nodurilor astfel incat exista o cale intre oricare doua noduri din cpc.
Pentru determinarea componentelor puternic conectate (cpc) dintr-un graf orientat vom folosi urmatorul graf orientat ca exemplu:
1->3, 3->2, 2->1, 3->4, 4->5, 5->7, 7->6, 6->4, 7->8
![]()
![]()
![]()
![]()
![]()
![]() 1 5
1 5
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 3 4 7 8
3 4 7 8
![]()
![]() 2 6
2 6
Vizitarea DFS dintr-un nod oarecare v produce o multime cu toate nodurile ce pot fi atinse plecand din v. Repetand vizitarea din v pentru graful cu arce inversate ca sens obtinem o alta multime de noduri, din care se poate ajunge in v. Intersectia celor doua multimi reprezinta componenta tare conexa care contine nodul v. Dupa eliminarea nodurilor acestei componente din graf se repeta operatia pentru nodurile ramase, pana cand nu mai sunt noduri in graf.
Pentru graful anterior vizitarea DFS din 1 produce multimea iar vizitarea grafului inversat din 1 produce multimea . Intersectia celor doua multimi reprezinta componenta tare conexa care contine nodul 1. Dupa eliminarea nodurilor 1,2 si 3, vizitarea grafului ramas din nodul 4 produce multimea , iar vizitarea din 4 a grafului cu arce inversate produce multimea , deci componenta tare conexa care-l contine pe 4 este . Ultima componenta cpc contine doar nodul
Este posibila imbunatatirea acestui algoritm pe baza observatiei ca s-ar putea determina toate componentele cpc la o singura vizitare a grafului inversat, folosind ca puncte de plecare nodurile in ordine inversa vizitarii DFS a grafului initial. Algoritmul foloseste vectorul t2 cu timpii de parasire ai fiecarui nod si repeta vizitarea grafului inversat din nodurile considerate in ordinea inversa a numerelor t2.
Pentru graful anterior vectorii t1 si t2 la vizitarea DFS din 1 vor fi:
nod i 1 2 3 4 5 6 7 8
t1[i] 1 3 2 5 6 8 7 10
t2[i] 16 4 15 14 13 9 12 11
Vizitarea grafului inversat se va face din 1 (t2=16) cu rezultat , apoi din 4 (t2=14) cu rezultat si din 8 (singurul nod ramas) cu rezultat .
Graful cu arce inversate se obtine prin transpunerea matricei initiale.
Pentru grafuri neorientate ce reprezinta retele de comunicatii sunt importante problemele de conectivitate. Un punct de articulare (un punct critic) dintr-un graf conex este un varf a carui eliminare (impreuna cu muchiile asciate) face ca graful sa nu mai fie conex. O 'punte' (o muchie critica) este o muchie a carei eliminare face ca graful ramas sa nu mai fie conex. O componenta biconexa este o submultime maximala de muchii astfel ca oricare doua muchii se afla pe un ciclu simplu. Fie graful conex cu muchiile:
Puncte de articulare: 3, 4, 5, 7
Muchii critice: 3-5, 7-8
Componente biconexe: (1,2,4), (5,6,7)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1 3 5 8
1 3 5 8
![]()
![]()
Un algoritm eficient pentru determinarea punctelor critice dintr-un graf conex foloseste vizitarea in adancime dintr-un varf radacina oarecare. Pentru graful anterior arborele DFS contine muchiile (1,2),(2,4),(4,3),(3,5),(5,6),(6,7),(7,8).
![]()
![]()
Un varf terminal (o frunza) din arbore nu poate fi punct de articulare, deoarece eliminarea lui nu intrerupe accesul la alte varfuri, deci varful 8 nu poate fi un punct critic. Radacina arborelui DFS poate fi punct de articulare numai daca are cel putin doi fii in arborele DFS, caci eliminarea ei ar intrerupe legatura dintre fiii sai. Deci 1 nu este punct de articulare. Un varf interior v din arborele DFS nu este punct de articulare daca exista in graf o muchie inapoi de la un varf u urmator lui v in arbore la un varf w anterior lui v in arbore, pentru ca eliminarea lui v din graf nu ar intrerupe accesul de la w la u. O muchie inapoi este o muchie de la un varf cu t1 mare la un varf cu t1 mic. Un nod u urmator lui v in arbore are t1[u] > t1[v], adica u este vizitat dupa v. De exemplu, t1[1]=1, t1[4]=3 , deci 4 este un descendent al lui 1 in arbore.
Pentru graful anterior varful 2 nu este punct critic deoarece exista muchia (4,1)
care permite accesul de la predecesorul lui 2 (1) la succesorul lui 2 (4); la fel 6 nu este punct critic deoarece exita muchia (7,5) de la fiul 7 la parintele 5. Varful 3 este punct de articulare deoarece nu exista o muchie de la fiul 5 la parintele sau 4 si deci eliminarea sa ar intrerupe accesul catre varful 5 si urmatoarele. La fel 4,5 si 7 sunt puncte critice deoarece nu exista muchie inapoi de la un fiu la un parinte.
Un alt exemplu este graful cu 4 varfuri si muchiile 1-2, 2-3, 3-4, 4-1
![]()
1 2 3 4
Arborele de explorare dfs are muchiile 1-2, 2-3, 3-4 si, in plus exista muchia inapoi de la 4 la 1; datorita acestei muchii varfurile 2 si 3 nu sunt puncte critice. 4 este frunza in arbore, iar 1 este radacina cu un singur fiu.
Daca se elimina muchia 1-4 din graful anterior atunci 2 si 3 devin puncte critice.
6 Grafuri implicite
O problema de optimizare discreta poate avea mai multe solutii vectoriale (sau matriciale) si fiecare solutie are un cost asociat; scopul este gasirea unei solutii optime pentru care functia de cost este minima sau maxima.
O serie de algoritmi de optimizare realizeaza o cautare intr-un graf, numit si spatiu al starilor. Acest graf este construit pe masura ce algoritmul progreseaza si nu este memorat integral, avand in general un numar foarte mare de noduri (stari). Graful este de obicei orientat si arcele au asociate costuri.
O solutie a problemei este o cale in graful starilor iar costul solutiei este suma costurilor arcelor ce compun calea respectiva.
Vom considera doua exemple clasice: problema rucsacului si iesirea din labirint.
Problema rucsacului are ca date n obiecte de greutate g[k] si valoare v[k] fiecare si un sac de capacitate t, iar cerinta este sa selectam acele obiecte cu greutate totala mai mica sau egala cu t pentru care valoarea obiectelor selectate este maxima. Solutia este fie un vector x cu valori 1 sau 0 dupa cum obiectul respectiv a fost sau nu selectat, fie un vector x cu numerele obiectelor din selectia optima (din rucsac).
Fie cazul concret in care sacul are capacitatea t=15 si exista 4 obiecte de greutati g[] = si valori unitare egale. Solutia optima (cu valoare maxima) este cea care foloseste obiectele 1,3 si 4.
In varianta binara vectorul solutie este x[] = , iar in varianta cu numere de obiecte solutia este x[]=.
Spatiul starilor pentru varianta cu x[k] egal cu numarul obiectului ales in pasul k si dupa eliminarea solutiilor echivalente:
![]()
![]()
![]()
![]()
![]()
![]() 6 5
6 5
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 4 4 3 4 3 2
4 4 3 4 3 2
(14) (13) (11) (10) (8)
8 6
![]()
![]()
(15) (13)
Arcele arborelui de stari au drept costuri greutatile (valorile) obiectelor, iar la capatul fiecarei ramuri este notata greutatea selectiei respective (deci costul solutiei). Solutiile optime sunt doua: una care foloseste doua obiecte cu greutati 6 si 8 si alta care foloseste 3 obiecte cu greutatile 2,4 si
Spatiul starilor in varianta binara este un arbore binar a carui inaltime este egala cu numarul de obiecte. Alternativele de pe nivelul k sunt includerea in solutie sau nu a obiectului k. La fiecare cale posibila este trecut costul insumat al arcelor folosite (valorile obiectelor selectate).

0 1




0 1 0 1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Problema iesirii din labirint ilustreaza o problema la care spatiul starilor nu mai este un arbore ci un graf care poate contine si cicluri.
Un labirint este reprezentat printr-o matrice L de carouri cu m linii si n coloane cu conventia ca L[i][j]=1 daca caroul din linia i si coloana j este liber (poate fi folosit pentru deplasare) si L[i][j]=0 daca caroul (i,j) este ocupat (de ziduri despartitoare).
Pornind dintr-un carou dat (liber) se cere drumul minim de iesire din labirint sau toate drumurile posibile de iesire din labirint, cu conditia ca un drum sa nu treaca de mai multe ori prin acelasi carou (pentru a evita deplasarea in cerc inchis, la infinit). Iesirea din labirint poate inseamna ca se ajunge la orice margine sau la un carou dat.
Fie un exemplu de labirint cu 4 linii si 4 coloane si punctul de plecare (2,2).
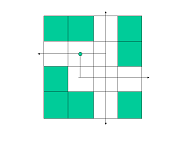
Cateva trasee de iesire si lungimea lor sunt prezentate mai jos :
2
Graful spatiului starilor pentru exemplul de mai sus arata astfel:
2,2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1,3 3,3
1,3 3,3
3,4 4,3
Nodurile fara succesori sunt puncte de iesire din labirint. Se observa existenta mai multor cicluri in acest graf.
Explorarea grafului pentru a gasi o cale catre un nod tinta se poate face in adancime sau in largime.
La explorarea in adancime se memoreaza (intr-o stiva vector) doar nodurile de pe calea in curs de explorare, deci necesarul de memorie este determinat de cea mai lunga cale din graf. Algoritmul "backtracking" corespunde cautarii in adancime.
La explorarea in largime se memoreaza (intr-o coada) succesorii fiecarui nod, iar numarul de noduri de pe un nivel creste exponential cu inaltimea grafului. Din punct de vedere al memoriei necesare cautarea in adancime in spatiul starilor este preferabila, dar exista si alte considerente care fac ca in unele situatii sa fie preferata o varianta de cautare in largime. Pentru grafuri cu ramuri de lungimi foarte diferite este preferabila o cautare in largime. In cazul labirintului, astfel de cai sunt trasee posibile de lungime foarte mare, dar care nu conduc la o iesire, alaturi de trasee scurte.
Pentru a evita ramanerea programului de explorare intr-un ciclu trebuie memorate carourile deja folosite; in principiu se poate folosi o multime de stari folosite, in care se cauta la fiecare incercare de deplasare din starea curenta. In problema labirintului se foloseste de obicei o solutie ad-hoc, mai simpla, de marcare a carourilor deja folosite, fara a mai utiliza o multime separata.
Timpul de rezolvare a unei probleme prin explorarea spatiului starilor depinde de numarul de noduri si de arce din acest graf, iar reducerea acestui timp se poate face prin reducerea dimensiunii grafului. Graful este generat dinamic, in cursul rezolvarii problemei prin "expandare", adica prin crearea de succesori ai nodului curent.
In graful implicit, un nod (o stare s) are ca succesori starile in care se poate ajunge din s, iar aceasta conditie (exprimata printr-o functie "posibil") depinde de problema rezolvata si de algoritmul folosit.
In problema rucsacului, functia "posibil" verifica daca un nou obiect poate fi luat sau nu in sac (fara a depasi capacitatea sacului), iar o stare corespunde unei selectii de obiecte. In problema labirintului functia "posibil" verifica daca este liber caroul prin care incercam sa ne deplasam din pozitia curenta.
Graful de stari se poate reduce ca dimensiune daca impunem si alte conditii in functia "posibil". Pentru probleme de minimizare putem compara costul solutiei partiale in curs de generare (costul unei cai incomplete) cu un cost minim de referinta si sa oprim expandarea caii daca acest cost este mai mare decat costul minim stabilit pana la acel moment. Ideea se poate folosi in problema iesirii din labirint: daca suntem pe o cale incompleta egala cu o cale completa anterioara nu are rost sa mai continuam pe calea respectiva.
Se poate spune ca diferentele dintre diferiti algoritmi de optimizare discreta provin din modul de expandare a grafului de stari, pentru minimizarea acestuia.
Cautarea in adancime in graful de stari implicit (metoda "backtracking") se poate exprima recursiv sau iterativ, folosind o stiva.
Pentru concretizare vom folosi problema umplerii prin inundare a unei suprafete delimitate de un contur oarecare, problema care seamana cu problema labirintului dar este ceva mai simpla. Problema permite vizualizarea diferentei dintre explorarea in adancime si explorarea in latime, prin afisarea suprafetei de colorat dupa fiecare pas.
Datele problemei se reprezinta printr-o matrice patratica in care elementele nenule reprezinta puncte de pe contur, iar elementele nule corespund unor puncte din interior care trebuie colorate. Se mai da un punct interior din care incepe colorarea (umplerea)
Vom marca punctele interioare colorate cu alta valoare (8) decat punctele de pe contur (1), pentru a pune in evidenta evolutia algoritmului. Vom considera drept punct initial punctul de coordonate (3,3).
Evolutia matricei la explorare in adancime a spatiului starilor:
Evolutia matricei la explorare in latime a spatiului starilor:
In coada sau in stiva vom pune adrese de celule (adrese de variabile structura):
typedef struct cell;
// construieste o variabila "cell"
cell * make (int i,int j)
Functia de umplere care foloseste o coada (explorare in largime) va fi:
void fillQ (int i, int j) ; // directii de extindere pe orizontala
int py[4] = ; // directii de extindere pe verticala
q=initQ();
pc=make(i,j); // construieste o variabila structura cu comp. i si j
addQ(q,pc); // adauga adresa la coada
while ( ! emptyQ(q) )
}
}
}
Functia de umplere cu exploare in adancime este la fel cu cea anterioara, dar foloseste o stiva in loc de coada. Stiva si coada au elemente de tip void* , fiind folosite si in alte aplicatii. Varianta recursiva de explorare in adancime este:
void fill (int i,int j )
}
}
Pentru cele mai multe probleme metoda "backtracking" face o cautare in adancime intr-un arbore binar sau intr-un arbore multicai. Varianta cu arbore binar (si vector solutie binar) are cateva avantaje: programe mai simple, toate solutiile au aceeasi lungime si nu pot apare solutii echivalente (care difera numai prin ordinea valorilor).
Exemplu de functie recursiva pentru algoritmul "backtracking" (solutii binare):
void bkt (int k)
x[k]=1; // incearca la stanga (cu valoarea 1 pe nivelul k)
if (posibil(k)) // daca e posibila o solutie cu x[k]=1
bkt (k+1); // cauta in subarborele stanga
x[k]=0; // incearca la dreapta (cu valoarea 0 pe niv. k)
bkt(k+1); // cauta in subarborele dreapta
}
Pentru problema rucsacului x[k]=1 semnifica prezenta obiectului k in sac (intr-o solutie) iar x[k]=0 semnifica absenta obiectului k dintr-o solutie. Pentru valoarea x[k]=0 nu am verificat daca solutia este acceptabila, considerand ca neincluderea unor obiecte in selectia optima este posibila intotdeauna.
Ordinea explorarii celor doi subarbori poate fi modificata, dar am preferat sa obtinem mai intai solutii cu mai multe obiecte si valoare mai mare.
Functia "print" fie afiseaza o solutie obtinuta (in problemele de enumerare a tuturor solutiilor posibile, deci a tuturor cailor posibile de la radacina la noduri terminale), fie compara costul solutiei obtinute cu cel mai bun cost anterior (in probleme de optimizare, care cer o solutie sau cale de cost minim sau maxim).
// daca obiectul k poate fi luat
int posibil (int k)
// afisare solutie
void print (void)
// calcul cost cale cu k arce
int sum (int k)
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3073
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved