Utilizarea primitivelor 'turtle graphics' pentru desenarea de curbe

In grafica 'turtle' o curba este generata prin deplasarea unui creion (cursor) virtual care poate fi imaginat ca reprezentand o broasca testoasa care se deplaseaza si lasa urme pe nisip. Directia de deplasare curenta (unghiul alfa format de aceasta cu axa Ox) poate fi schimbata prin apelurile stanga() dreapta() iar trasarea pe directia curenta a unui segment de lungime l se face cu apelul inainte(l). Deplasarea inapoi poate fi realizata in doua moduri: cu ajutorul apelului inapoi() cursorul se deplaseaza inapoi pe distanta l, fara a desena o linie, iar cu apelul inapoi_sterge() deplasarea este insotita de stergerea liniei pe care ea se face; in ambele cazuri 'broscuta testoasa' isi pastreaza orientarea. Pozitia initiala a cursorului virtual se stabileste prin apelul functiei initpoz() care precizeaza coordonatele punctului initial si orientarea initiala a 'broscutei'

In implementarea algoritmilor pentru desenarea curbelor descrise mai jos, se recomanda crearea unui fisier cu operatiile fundamentale pentru grafica 'turtle'. Prototipurile functiilor care implementeaza aceste primitive sunt listate in continuare.

void stanga(double s);

void dreapta(double s);

void inainte(double l);

void inapoi(double l);

void inapoi_sterge(double l);

void initpoz(int x, int y, double u);

In cazul unghiurilor argumentul corespunzator al functiilor este exprimat in grade, dar trebuie notat ca functiile trigonometrice cer argumente exprimate in radiani. Lungimile deplasarilor vor fi exprimate in pixeli.

Este recomandabil ca pozitia curenta a creionului virtual si orientarea curenta sa fie retinute in variabile globale.

Curba 'Pom'

Curba 'pom' este una dintre curbele care se pot defini recursiv. In Figura 1 sunt prezentate curbele de ordin 1, 2, 3 si 4, la care ramurile au aceeasi lungime. Este posibil ca la apelul functiei care deseneaza curba de ordin inferior, lungimea laturilor sa fie inmultita cu un factor de scala (lungimea laturilor va creste sau se va micsora dupa cum factorul va fi supra sau subunitar). In Figura 2 este prezentata o curba 'pom' de ordinul 4 cu 'tulpina'.

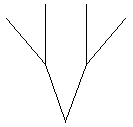
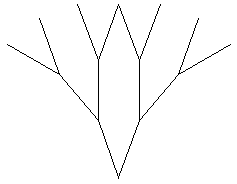
Figura 1 - Curbele 'pom' de ordin 1, 2 si 3

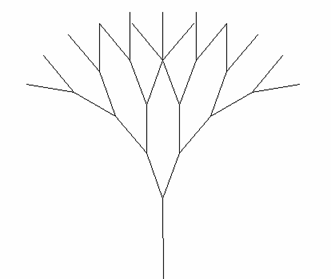Figura 2 - Curba 'pom' de ordin 4 cu 'tulpina'

In Figura 3 sunt prezentate miscarile pe care trebuie sa le efectueze cursorul generalizat (broscuta testoasa), pentru desenarea unei curbe de ordinul i. Pornind de la orientarea de baza a desenului, se executa o rotatie la stanga cu unghiul a (Figura 3 a) ) urmata de o deplasare inainte de lungime L (Figura 3 b) ), desenarea unei curbe 'pom' de ordin i - 1 cu ramurile de lungime L*coeficient_de_scara (Figura 3 c) ). Cursorul reculeaza pe o distanta L fara sa traseze linie, dupa care se roteste la dreapta cu unghiul a+b si se deplaseaza inainte cu L (Figura 3 d), e) si f) ). Pe aceasta pozitie se deseneaza o curba 'pom' de ordinul i-1, dupa care cursorul reculeaza pe o distanta L fara sa traseze linie si in final se roteste la stanga cu unghiul b (Figura 3 g) si h) ).

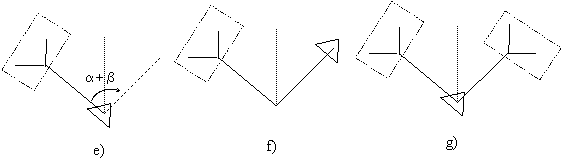
Figura 3 - Modul de desenare al curbelor 'pom' cu 'turtle graphics'

Curba dragonului (Knuth)

Curba dragonului (Knuth) este un fractal la care generatorul este construit astfel incat directia de expandare sa alterneze de o parte si de cealalta a laturilor poligonului initiator. O astfel de curba are proprietatea ca poate pava (umple) o suprafata plana. 'Golurile' delimitate de frontiera unei curbe dragon pot fi 'umplute' cu curbe dragon similare, de dimensiune mai mica.

In Figura 4 este prezentata curba dragonului de ordinul 5. Curba de ordin 8 este prezentata in imaginea din Figura 5, iar in Figura 6 este desenata curba dragonului de ordin 10.

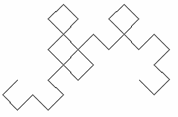
Figura 4 - Curba dragonului de ordinul 5

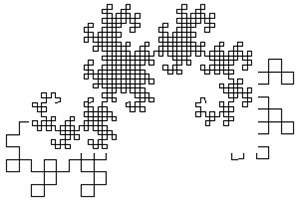
Figura 5 - Curba dragonului de ordinul 8

Figura 6 - Curba dragonului de ordinul 10

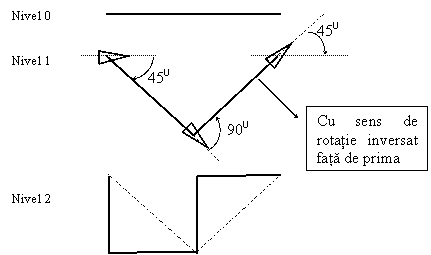
Curba de nivel 0 este un segment de dreapta de lungime L. Curba de nivel 1 se obtine desenand catetele unui triunghi dreptunghic isoscel care ar avea drept ipotenuza curba de nivel 0. Fiecare element al curbei de nivel 2 se construieste dupa acelasi algoritm, luand drept curbe generatoare segmentele de dreapta din curba de nivel 1 (Figura 7). Pentru curba de nivel 2, in Figura 7 sunt prezentate miscarile cursorului generalizat. Se remarca schimbarea sensului de rotatie la fiecare segment fata de sensul asociat segmentului anterior.

Figura 7 - Curba dragonului de nivel 0, 1 si 2

Curba lui Koch

O definitie recursiva pentru acest tip de curba este data mai jos:

Curba Koch de ordinul 0 este un segment de dreapta (de lungime L).

Curba Koch de ordinul k+1 se obtine impartind fiecare din segmentele componente ale curbei Koch de ordin k in 3 parti egale si inlocuind segmentul din mijloc (fie el T) cu celelalte doua laturi ale unui triunghi echilateral care are ca baza pe T.

In Figura 8 sunt prezentate curbele Koch de ordin 0, 1 si 2, iar in Figura 9 deplasarile cursorului generalizat (rotatiile si translatiile broscutei testoase) care trebuiesc efectuate pentru a construi curba de ordin 1.

Figura 8 - Curbele Koch de nivel 0, 1 si 2

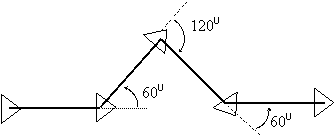
Figura 9 - Elementele 'turtle graphics' pentru curba Koch de nivel 1

O curba 'fulg de zapada' este formata din trei curbe Koch rotite fiecare cu 120 . Un element al fulgului de nivel 1 este prezentat in Figura 10.

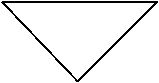
Figura 10 - Curba 'fulg de zapada' de ordinul 0

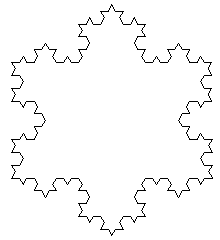
Elementele fiecarei curbe 'fulg' de ordin k au dimensiuni de 3 ori mai mici decat ale curbei de ordin k-1. In Figura 11 este prezentata o astfel de curba.

Figura 11 - Curba 'fulg de zapada'

Curbele lui Peano

Curbele lui Peano de diferite ordine, ca si miscarile cursorului generalizat pentru desenarea curbei de ordin 1 sunt prezentate in Figura 12. Deoarece aceste curbe sunt inchise, la implementarea functiei recursive pentru desenarea corecta a acestei curbe trebuie tinut seama de cumularea erorilor.

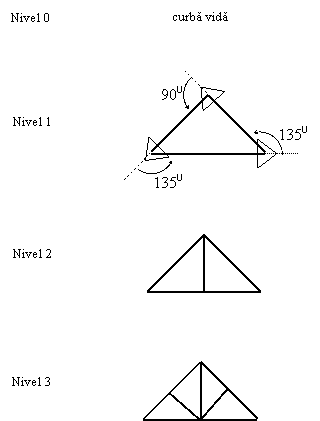
Figura 12 - Curbele lui Peano de nivel 0, 1, 2 si 3

Curba Peano-Gosper

In cazul curbei Peano-Gosper, daca se considera ca initiatorul (curba de ordinul 0) are lungimea L, atunci generatorul (curba de ordinul 1) va fi format din k=3 segmente, fiecare avand o lungime . Daca se noteaza cu a unghiul CAB, stiind ca unghiurile ACD si CDB au 120 se obtine: cos(a)= sin(a)=

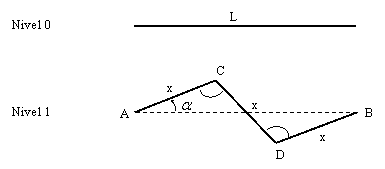
Figura 1 - Curbele Peano-Gosper de nivel 0, 1

Curbele lui Sierpinski

Un alt reprezentant al familiei curbelor autoasemenea sunt curbele lui Sierpinski, prezentate in Figura 14. Studentii vor defini modul in care trebuie sa se deplaseze cursorul generalizat pentru a desena recursiv aceste curbe. Curba de ordinul k este formata din curbe de ordin inferior (k-1) conectate intre ele prin segmente de dreapta de dimensiuni si orientari conform desenului din Figura 14 (segmentele de legatura sunt desenate cu culorile rosu, albastru, verde).

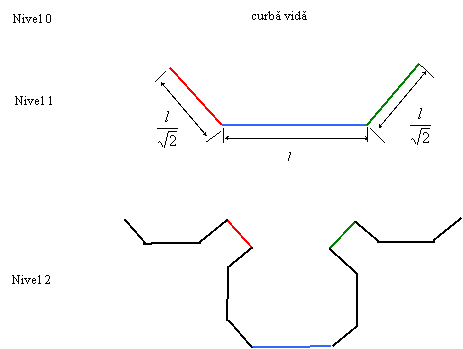
Figura 1 - Curbele lui Sierpinski de nivel 0, 1 si 2

Curbele Hilbert

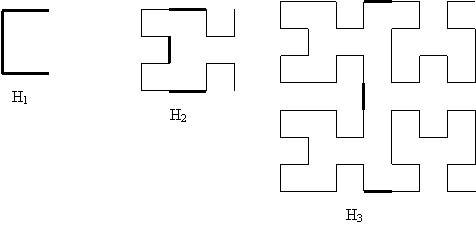
Figura 1 - Curbele Hilbert de nivel 1, 2 si 3

Curbele Hilbert au fost prezentate in Cursul 2 in varianta de abordare recursiva, in care fiecare curba este trasata prin apelul recursiv al unor functii care deseneaza curbe de nivel inferior, conectate intre ele prin segmente de dreapta de aceeasi lungime cu elementele curbelor pe care le leaga. In Figura 15 sunt prezentate curbele de nivel 1, 2 si 3, curbele de nivel 0 fiind curbe vide. Aceste curbe vor fi utilizate pentru a se defini miscarile cursorului generalizat care conduc la desenarea lor.

Figura 1 - Curbele Hilbert de nivel 1, 2 si 3

In Figura 16 sunt prezentate curbe de diferite ordine care umplu un spatiu de forma patrata, pozitionate astfel incat elementele lor sa nu se suprapuna.

Labirint

Un labirint poate fi reprezentat ca o matrice, in care celulele pot sa comunice sau nu cu celulele vecine situate la E, S, V sau N (pentru celulele situate la periferia labirintului, comunicarea se poate face cu exteriorul). In Figura 17 este indicat modul de reprezentare a peretilor despartitori cu sau fara trecere intre celulele pe care le separa.

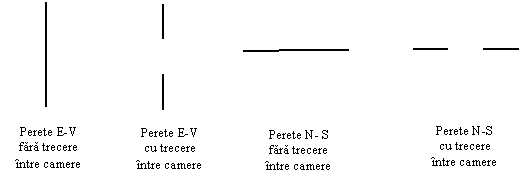
Figura 1 - Reprezentarea peretilor camerelor din labirint

Teme de casa propuse

Identificarea subgrupelor se face in concordanta cu pagina de web a cursului, in care este indicat in mod corespunzator numele asistentului care lucreaza cu fiecare subgrupa.

Grupa 311CA - semigrupa a

Sa se scrie un program care deseneaza curbele Peano-Gosper de ordin n utilizand o functie recursiva si elemente 'turtle graphics'. Se va considera ca initiator un hexagon regulat, ale carui laturi se considera curbe Peano-Gosper de ordin 0.

Grupa 311CA - semigrupa b

Sa se scrie un program care traseaza curbele lui Sierpinski pana la ordinul n utilizand o functie recursiva si elemente 'turtle graphics'. Curbele vor umple cat mai bine ecranul, indiferent de dimensiunile acestuia.

Grupa 312CA - semigrupa a

Sa se scrie un program care deseneaza o curba 'pom' utilizand elemente de 'grafica turtle'. Fiecare 'pom' desenat are lungimea segmentelor redusa cu un factor de scara fata de predecesorul sau (curba 'pom' de ordin superior). 'Radacina pomului' va fi plasata la mijlocul laturii de jos a ecranului, 'pomul' va avea o 'tulpina' de lungime aleasa de utilizator, parametrii de intrare ai programului fiind: ordinul curbei desenate, lungimea pentru prima 'ramura' desenata, precum si unghiurile a si b

Grupa 312CA - semigrupa b

Sa se traseze curbele Hilbert de ordin 1 pana la n definind o functie recursiva care utilizeaza primitivele 'turtle graphics'. Punctele initiale ale curbelor de diferite ordine vor fi astfel pozitionate incat elementele acestor curbe sa nu se suprapuna, ci eventual sa se intersecteze (ca in Figura 16).

Grupa 313CA - semigrupa a

Utilizand elemente de grafica 'turtle' sa se vizualizeze cautarea drumului de iesire printr-un labirint, cautare realizata prin aplicarea unei functii backtracking. Drumul de la o celula a labirintului la celula vecina se deseneaza ca un segment de dreapta care uneste centrele celor doua celule. La retragerea incercarii, segmentul respectiv va fi sters. Programul va primi ca date descrierea labirintului si pozitia initiala de la care se cauta iesirea.

Grupa 313CA - semigrupa b

Sa se deseneze curba dragonului (Knuth) utilizand o functie recursiva si elemente de grafica turtle. Datele de intrare ale programului vor fi: ordinul curbei, lungimea segmentului pentru curba de nivel 0 si coordonatele punctului in care trebuie sa se afle cursorul grafic in momentul inceperii trasarii curbei.

Grupa 314CA

Sa se implementeze un program care sa deseneze o curba fulg cu ajutorul unei functii recursive pentru desenarea curbei Koch utilizand elemente de grafica 'turtle'

Grupa 315CA

Sa se implementeze un program care sa deseneze curbele lui Peano utilizand o functie recursiva cu elemente de grafica 'turtle'