| CATEGORII DOCUMENTE |
| Asp | Autocad | C | Dot net | Excel | Fox pro | Html | Java |
| Linux | Mathcad | Photoshop | Php | Sql | Visual studio | Windows | Xml |
DOCUMENTE SIMILARE |
||
|
||
because if you have the localised version of GSETUP.EXE installation program, and you have a localised ArchiCAD.FON file which in compressed form has the name ArchiCAD.FO_, and you have the Microsoft COMPRESS.EXE compression utility, and you are familiar with the structure of GSETUP.INF, then you need only a simple text editor, and you can do all the changes you want to.
because, the ArchiCAD for Windows package consists of 500 to 600 files, requires about 15 Megabytes of hard disk space. The ArchiCAD.EXE executable program itself is more than 3.5 Megabytes, so that one must cut it into smaller parts even in compressed form to fit in the available 1.44 Megabyte free space of a floppy diskette. Furthermore you have to group the files together, into so called items, to provide the possibility of partial installation. To give a hand to manage the packaging we provide the PREPARE.EXE utility.
The file content arranged into 7 sections, in the following order:
|
Section Name |
Description |
|
[Application] |
Default directory, drive, Release number. |
|
[Profile] |
Information on ArchiCAD.INI file, this section contains the ArchiCAD version name. |
|
[ItemGroups] |
List of eligible items for partial installation. |
|
[Disks] |
List of diskettes needed to install the product, and the name of each diskette. |
|
[Dirs] |
List of the necessary directories from the destination directory. Files to be copied must be in the same directory structure on the floppy disks. |
|
[Files] |
List of files. The format of these entries described later in details. |
|
[PM Info] |
Program Manager item descriptions. |
|
[End] |
It is not a section it's merely a terminating symbol. |
1. Comment lines
The lines beginning with semicolon, are comment lines:
; Module name: GSetup.Inf
(I mean that if the first non white space character is ';', even in the scope of a macro, but not in the beginningpart,.)
2. Simple macro
The Gsetup provides a simple macro definition possibility, especially useful in the [File] section. The form of the macro definition is:
<beginningpart %1 endpart>
All the subsequent lines
line
are interpreted as:
beginning part line endpart
until a macro off command is meet:
<->
Once you switch off the last defined macro, you can switch it on again by issuing the :
<+>
command.
3. The entries in the sections:
A string entry in the [Application], [Profile], [ItemGroups], [Disks] and [Dirs]
sections must have the following form:
[section]
entry=string
.
.
.
The [Application] and the [Profile] sections have fixed number of entries, while the others may have variable number of entries depending on the content of the package.
3.1 The entries in the [Application] section look like this:
[Application]
;Application global information
AppName=ArchiCAD 4.1 Installation
DefDrive=C:
DefDirName=ArchiCAD
DefPMGroup=AC416R3.GRP, ArchiCAD
Where the 'AppName' entry specifies the window title for the installation dialogs:
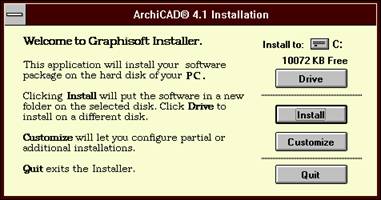
'DefDrive' specifies the initial drive to install to, while 'DefDirName' tells the name of the directory to create in the easy install, if there is no such directory yet. If the directory exists, Gsetup will create a directory using an extension of 'NEW', or 'N01' or 'N02' or 'N99' (e.g. ArchiCAD.NEW).
The 'DefPMGroup' entry has two parameters separated by a coma. The first is the name of the Program Manager group file name that is to be created in the windows directory, the second is the name of the Program Manager group. If there is a Program Manager group already exists, that will be used, even if the file name is different.
3.2 The entries in the [Profile] section look like this:
Profile]
; Application INI file Information;
ProfileName=ArchiCAD.ini
ArchiCADSectionName=ArchiCAD 4.16 R3 INT
SystemDirEntryName=PrefsAndDriverDirectory
During the installation if the first itemGroup is selected, the Gsetup creates the file given in the ProfileName to the windows directory, and ceates a section in it, which tells the ArchiCAD program, where to find the Plotware and Digware folders:
ArchiCAD.ini file:)
[ArchiCAD 4.16 R3 INT]
PrefsAndDriverDirectory=C:ArchiCAD
The ArchiCAD version string must be the same, if you change the ArchiCAD program in the package, yo have to change accordingly the ArchiCADSectionName entry in the GSETUP.INF.
If the user chooses the customized installation, and the ArchiCAD.ini file already exists, the directory to install to will be the directory specified in the PrefsAndDriverDirectory item.
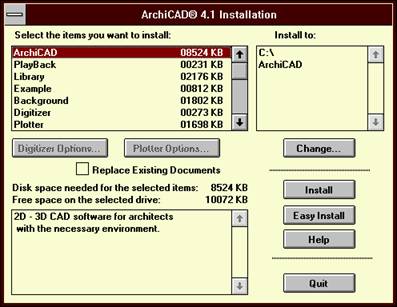
3.3 The entries in the [ItemGroups] section:
The entries in this section has the fooowing form:
number = ItemNameString , ItemInfoString
where the number runs from 1 to n , 1 < n and n < 25.
the ItemNameString is the string that appears in the select listbox
the ItemInfoString is the string that may appear in the Info listbox, where the '' can be used as line separator.
The first entry must be the ArchiCAD ,
the Digitizer and the Plotter item must have a terminating colon, and must be the same as in the Gsetup resource file, otherwise the Options buttons will not work.
[ItemGroups]
;List of eligible items for partial installation.
1=ArchiCAD , 2D - 3D CAD software for architects with the necessary environment.
2=PlayBack , Animation utility for playing ArchiCAD BMS format files.
3=Library , Sample 3D object library.
4=Example , Archive (with library) and Floor Plan Files.
5=Background , Background Pictures for 3D projections.
6=Digitizer: , Digitizer support.Press the Digitizer Options button to select the drivers you need.
7=Plotter: , Plotter support.Press the Plotter Options button to select the drivers you need.
8=Shaders for RenderMan , RenderMan RIB support.
3.4 The entries in the [Disks] section:
The entries in this section has the fooowing form:
number = ItemNameString
where the number runs from 1 to n , 1 < n and n < 25.
These numbers serves for further references in the [Files] section.
The ItemNameString appears in the insert disk dialog:
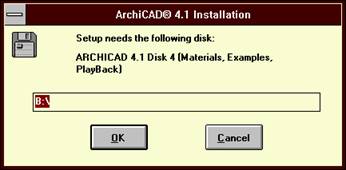
[Disks]
;List of diskettes needed to install the product and the name of each diskette.
1=ARCHICAD 4.1 Disk 1 (ARCHICAD Program Part 1)
2=ARCHICAD 4.1 Disk 2 (ARCHICAD Program Part 2)
3=ARCHICAD 4.1 Disk 3 (ARCHICAD Library)
4=ARCHICAD 4.1 Disk 4 (Materials, Examples, PlayBack)
5=ARCHICAD 4.1 Disk 5 (Digitizer and Plotter Drivers)
3.5 The entries in the [Dirs] section:
The entries in this section has the fooowing form:
number = ItemNameString
where the number runs from 1 to n , 1 < n and n < 100.
These numbers serves for further references in the [Files] section.
The ItemNameString is the realtive path from the default library.
The firts entry must be:
1=.
This is the reference for the default library.
The a child directory always must have its parent in the list,with a number less than the number of the child.
This order is good:
6=ARCHICAD.LIB
7=ARCHICAD.LIB01600MAT
This would be wrong:
6=ARCHICAD.LIB01600MAT
7=ARCHICAD.LIB
(It is because the Gsetup does not try to sort the library list.)
[Dirs]
;lists of directories that must be created from the destination directory
;files to be copied are in the same directory structure on the
;floppy disks (by default)
2=SHADERS
3=BKGROUND
4=EXAMPLES
5=DIGWARE
6=ARCHICAD.LIB
7=ARCHICAD.LIB01600MAT
8=ARCHICAD.LIB01GENERA
9=ARCHICAD.LIB01GENERA01070SYM
10=ARCHICAD.LIB01GENERA01200OFF
11=ARCHICAD.LIB01GENERA01800MIS
12=ARCHICAD.LIB02SITEWO
.
.
.
62=ARCHICAD.LIB16ELECTR16700COM
63=ARCHICAD.LIB16ELECTR16900CON
64=ARCHICAD.LIB17SPORTS
65=ARCHICAD.LIBINTERNAL
66=ARCHICAD.LIBPROPERTI
67=PLOTWARE
3.6 The entries in the [Files] section:
The number of files must be less than 1500 in the current version of Gsetup.
|
line format: |
ItemGroup#,description,name,size,dir#,diskette#,Compressed |
The ItemGroup#, dir# and diskette# are the corresponding numbers from the [ItemGroups], [Dirs], and [Disks] sections.
The Compressed is can be Y or N, indicating that the file is compressed or not.
The description is the comment of the file copying dialog. In case of plotter and digitizer drivers, these strings appear in the driver lists of the options dialog.
The name is the dos file name. If the file was compressed with the -r options (rename the file),it must be the new name, as it is on the dirtibution diskettes.
The size is the original size i.e. the extracted size, and you must give it exactly. The only exeption is the case of a split file, like the ArchiCAD.EXE. The split file contains itself the original size information.
[Files]
;ItemGroup#, description, name, size, (dir #), (diskette #), (Compressed)
1, Read Me File, Read_me.txt, 7011, 1, 1, n
1, Font File, Archicad.fo_, 29584, 1, 1, y
1, Program File-1, ArchiCAD.E1_, 4000000, 1, 1, Y
1, Program File-2, ArchiCAD.E2_, 4000000, 1, 2, Y
3, Read Me File, Readme_L.txt, 2215, 6, 3, n
< 3, Files (CARS), %1 , 7, 3, Y>
01621C1F.GS_, 3691
01621C1R.GS_, 2424
01621C1S.GS_, 2935
<7,%1,67, 5,Y>
Benson 1624-SB.,BN1624SB.DL_, 22288
Benson 1825-SB.,BN1625SB.DL_, 22288
Benson 1625-SR.,BN1625SR.DL_, 22304
.
.
.
Do not forget to place a
<->
macro off command at the end of the [Files] section.
3.7 The entries in the [PM Info] section:
The number of entries in this section must be less than 50.
|
line format: |
FileNameAndOptionalParameters,App.Description,IconFile,Icon# |
This section describes the items to be placed into the program manager group after the installation completed successfully. The IconFile and the Icon# icon number are optional parameters. You have to avoid using special characters (e.g. ' or ' ) in the App.Description. The app description part will appear in the group, under the icon of the item.
[PM Info]
;File Name, App. Description, Icon file, Icon #
ArchiCAD.EXE, ArchiCAD 4.1
PlayBack.EXE, PlayBack 1.5
Read_Me.TXT, Read Me First
ArchiCAD.HLP, ArchiCAD Help
ArchiCAD.EXE citybloc.pln, Cityblock Plan, ArchiCAD.EXE, 3
ArchiCAD.EXE example.pla, Example, ArchiCAD.EXE, 3
README_L.TXT, Read Me Library
READPLAY.TXT, Read Me PlayBack
READMESH.TXT, Read Me Shaders
[End]
Remember that Gsetup reqiures the
[End]
at the end of the file.
4 The packaging:
4.1 Splitting:
If you start the installer while holding down the Ctrl key, you get a file open dialog,where you can select from a combo box the size of the first and the further parts of the file to be splitted, and you can select the file as well.
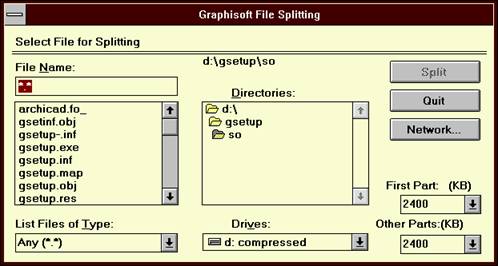
Then if you selected the file and presses
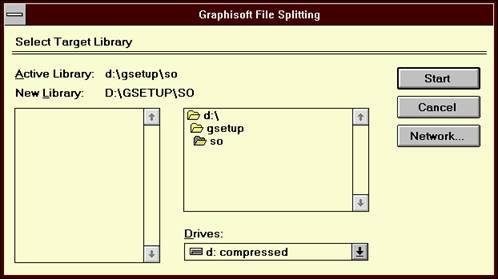
where you can select the target library.
4.2 Compressing files
To compress a single file you can use the Microsoft COMPRESS.EXE compression utility, form a dos prompt:
Compress -r filename destinationDirectory
To prepare compression for the ArchiCAD package, you can use the PREPARE.EXE
This program allows you to select a complete folder for packaging, and an other as the destination. It creates the directories and two files in the destination folder. The first is the DOCOMPR.BAT and the second is the COMPRESS.LOG. Then it asks whether it should immediately execute the DOCOMPR.BAT file, which places the compressed files in the right place. It will compress all the files found in the specified directory. If you wish to ship some files in uncompressed form you have to replace those in the destination directory with the original ones. An other problem may come from the renaming if there are files with almost the same names differing only at the last character, and placed in the same directory. In this case COMPRESS.EXE will overwrite the files. This is the case e.g. with the RIB shader files.You can compress them withouth renaming, or you can leave them in uncompressed form:
<8,,%1,2,4,N>
ACDEPTHC.SL, 229
ACDEPTHC.SLO, 731
ACSHADER.SL, 684
ACSHADER.SLO, 2206
READMESH.TXT, 2007
<->
The COMPRESS.LOG file has the same strucure as the GSETUP.INF.
The main difference is that in the [Files] section the references for the ItemGroup# and diskette# is dummy : +ITEMGROUP+ and +DISK+.
Now you can decide how to arrange the files on the diskettes, how to make the groups, and you can replace the dummy with the real values.
Remember that ArchiCAD.FO_ and GSETUP.INF must be placed in the same directory as the GSETUP.EXE, and that they dont have to appear in the GSETUP.INF .
Be sure, that the diskette# parameters are placed in growing order in the GSETUP.INF file, otherwise the program asks the user to chage the diskettes back and forth.
4.3 Changing One Item in the package:
If it is referenced in Program Manager Group:
If the name changed, you have to change it.
In the Program Manager section you have to use the original name!
If it has to be split:
You have to split first, than you can compress.
If it is the ArchiCAD:
You have to split first, than you can compress.
Dont forget changing the version string in all occurances.
If it is a plotter or digitizer driver:
You can ask the ArchiCAD to show the full name of the driver, or you can use the PREPARE.EXE.
If it is a file mentioned above or if it is a file not mentioned above:
If the name changed, you have to change it.
If the size changed, you have to change it.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1603
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved