| CATEGORII DOCUMENTE |
| Arhitectura | Auto | Casa gradina | Constructii | Instalatii | Pomicultura | Silvicultura |
1. RECAPITULARE NOTIUNI DE BAZA
1.1. Diagrama s e pentru beton
Diagrama s e la incercarea la compresiune monoaxiala si la cea de intindere monoaxiala este reprezentata in fig. 1.1.
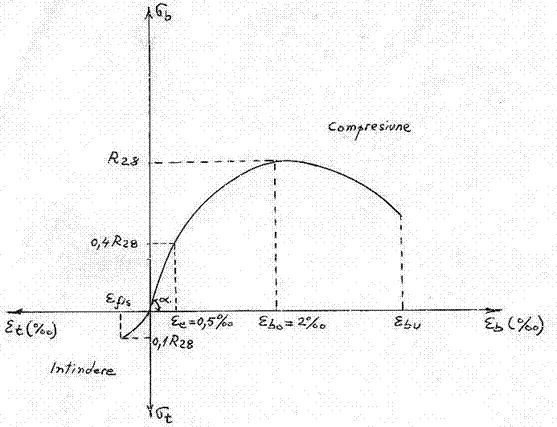
Punctele caracteristice ale diagramei:
ee se = (0,40,5) R28 - limita la compresiune a domeniului elastic,
- relatia s e, in domeniul elastic, conform legii lui Hooke:
s = Eb * e
unde Eb = tg a = modulul de elasticitate longitudinal
eb0 s R28 - limita rezistentei la compresiune centrica, la 28 de zile,
ebu s < R28 - limita ultima la compresiune centrica,
efis sf = (0.10.2)*R28 - limita rezistentei la intindere centrica, la 28 de zile,
Concluzia: betonul este un material foarte fragil, datorita valorilor deosebit de reduse ale deformatiilor specifice ultime, atat la intindere cat si la compresiune.
Armaturile din otel moale prezinta practic aceeasi alura a curbei .
In practica, pentru efectuarea calculelor de proiectare de rezistenta, se utilizeaza diagrama biliniara din fig. 2.2.
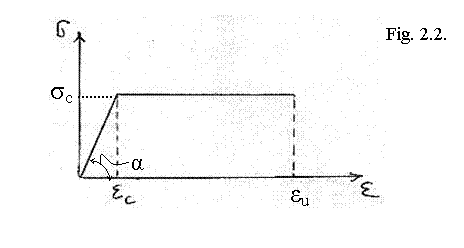
Punctele caracteristice ale diagramei:
ec sc - limita de curgere
- conform legii lui Hooke:
sc = Eec ec sc/E
unde E = 2,1x 106Kgf/cm2
- valorile limitei de curgere:
sc = 2850 Kgf/cm2 pt. otel OB37
sc = 3500 Kgf/cm2 pt. otel PC52
sc = 4000 Kgf/cm2 pt. otel PC60
- rezulta ca:
ec = 2850/(2.1*106) = 1.4 pt. otel OB37
ec = 3500/(2.1*106) = 1.7 pt. otel PC52
ec = 4000/(2.1*106) = 1.9 pt. otel PC60
eu su - limita ultima
eu = 50 o oo cand intervin solicitarile seismic
eu = 15 o oo in celelalte cazuri
Otelurile produse in Romania, laminate la cald, prezinta curbe s e cu palier de curgere; totusi, otelurile de tip PC pot sa nu aiba un palier de curgere, neimpus de standarde.
ELEMENTE INTINSE CENTRIC
2.1. Relatii de calcul pentru dimensionarea elementelor din beton armat solicitate la intindere centrica
Solicitarea simpla la intindere centrica nu exista in realitate datorita:
- imperfectiunilor barelor si
- impreciziei aplicarii aplicarii fortei.
Se aplica pentru elementele structurale din beton armat la care intinderea centrica este predominanta (peretii rezervoarelor pentru lichide, barele intinse ale grinzilor cu zabrele, tirantii arcelor).
Predimensionarea elementelor intinse centric se efectueaza pentru una din cele doua situatii :
a) Predimensionarea din conditia neadmiterii fisurarii in exploatare.
Betonul intins fisureaza pentru valoarea deformatiei (alungirii) specifice de 0,1 o oo
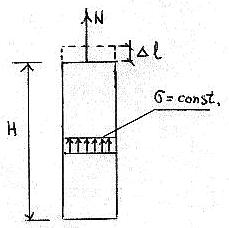Fig. 5.3.
Deoarece e = constant pe intreaga sectiune (e Dl / H) , rezulta :
s =N/A = ea * Ea = constant (fig. 5. 3).
Datorita conlucrarii si aderentei dintre beton si armatura, alungirile si deformatiile specifice ale betonului si armaturii vor fi egale.
ea eb
Conform diagramei s e
eb 0,1 o oo Ea = 2,1x106 kg/cm2
Rezulta ca
sa ea * Ea = (0,1/1000)x2,1x106 200 kg/cm2
Rezulta ca, atunci cand elementul structural din beton armat, supus la intindere centrica fisureaza, in armatura se dezvolta un efort foarte redus in comparatie cu limita sa de curgere si anume, cca 200kg/cm2.
Forta totala in armatura in momentul fisurarii va fi
saAa = 200Aa
si reprezinta contributia armaturii la preluarea fortei de fisurare.
Aportul betonului va fi
sbfisAb.
Raportul intre rezistenta maxima la compresiune Rb si rezistenta la intindere Rt a betonului este, de regula, egal cu 10:
sbfis Rt = Rb/10
In acest caz sbfisAb = AbRb/10, iar ecuatia de echilibru va fi :
Nf = AbRt + Aasa = AbRb/10 + 200Aa
Conditia de rezistenta si de predimensionare este:
N Nf / c
Valoarea coeficientului de siguranta pentru fisurare este
c = 1,31,5.
In cazul elementelor care lucreaza fara fisuri:
- betonul trebuie sa aiba o rezistenta la intindere cat mai mare,
- armaturile pot avea limita de curgere mai redusa, avand in vedere efortul unitar de cca. 200kg/cm2 .
b) Predimensionarea din conditia de siguranta la rupere, se aplica pentru elementele de beton armat la care se accepta un anumit grad de fisurare si care sunt protejate impotriva coroziunii ce se dezvolta datorita fisurarii.
Betonul fisurat, nu mai poate prelua forta axiala de intindere (sb = 0, deoarece eb > 0,1 o oo ), deci ruperea elementului intins se va produce odata cu intrarea in curgere a armaturii intinse.
Conditia de predimensionare este
N Nr/c = Aa.sc/c,
unde c = 2 =coeficientul de siguranta.
Este recomandabil ca:
- sa se aleaga armatura cu limita de curgere ridicata (de tip PC).
- armaturile sa se dispuna cat mai compacte, betonul avand numai rol de protectie.
2.2. Elemente structurale solicitate la intindere centrica
2.1. Tiranti la arce din beton armat
Rolul
structural al tirantilor este de a prelua impingerile transmise de arce in
punctele de rezemare.
p p
'A'
Efortul in tirant va fi:
2.1. Bare intinse la grinzi cu zabrele din beton armat
P P
|
P |
|
T |
|
T |
|
T |
|
T |
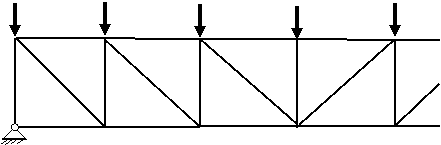
Barele intinse, notate cu T, sunt diagonalele si talpa inferioara.
2.3. Probleme de baza la elementele structurale intinse centric:
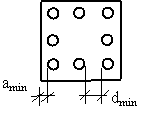
- barele de armatura se vor dispune cat mai compact, dimensiunile sectiunii barelor intinse fiind dictate din conditia tehnologica de asigurare a betonarii si a compactarii,
- armaturile se vor ancora in zone cu eforturi de compresiune normale pe directia barelor ce se ancoreaza,
- zonele de ancorare a barelor intinse trebuie conformate corespunzator.
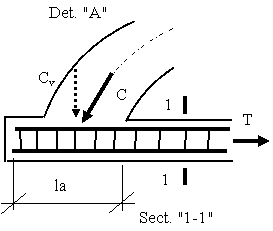
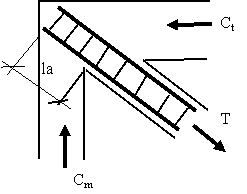
2. Exemple de rezolvare a ancorarii barelor intinse:
- in cazul tirantilor arcelor, comprimarea zonei in care se ancoreaza barele intinse este asigurata de efortul de compresiune din arc,
- in cazul diagonalelor intinse ale grizilor cu zabrele, comprimarea zonei de ancorarea a barelor din diagonala intinsa este asigurata de eforturile de compresiune din talpa superioara si din montant.
Det. 'B'
3. ELEMENTE INCOVOIATE
2.1. Relatii de calcul pentru dimensionarea elementelor din beton armat solicitate la incovoiere pura
Se observa
ca mn = rdj iar arcul de cerc
mn situat la distanta y fata de axa neutra va avea
lungimea mn = (r + y) dj Alungirea va fi, in consecinta: mn mn = (r + y) dj rdj = ydj iar alungirea
specifica:
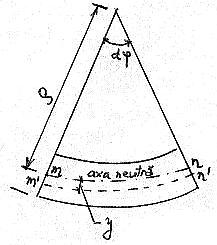Fig. 5.4.
Rezulta ca, pentru elementele incovoiate, deformatia specifica nu mai este constanta pe sectiune (ca la intindere/compresiune centrica), ci variaza linear pe inaltimea sectiunii :
e = y/r
Cand y = 0, in axa neutra, deformatiile specifice sunt nule.
La extremitati:
(y = + h/2 pentru o sectiune simetrica),
e este maxim (alungire, respectiv scurtare) .
Fibrele superioare fata de axa neutra se scurteaza, iar fibrele inferioare (sub axa neutra) se alungesc.
Numai in domeniul elastic, betonul armat respecta legea lui Hooke
s = Ee = E y/r
Abordarea stabilirii valorilor eforturilor unitare si a deformatiilor specifice pentru o bara de beton armat incovoiata va fi diferita de abordarea cunoscuta, pentru materiale omogene si care lucreaza in domeniul elastic.
Ideea fundamentala este aceea ca eforturile interioare produse in beton si in armatura (fig.5.5), oricare ar fi distributia lor, echilibreaza solicitarea exterioara.
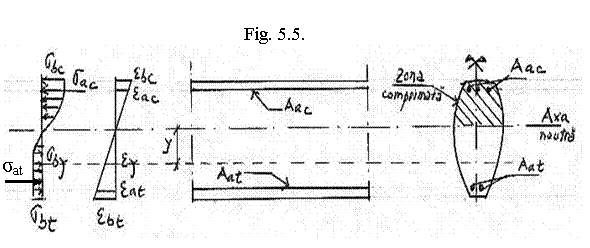
Eforturile in beton si in armatura, ca si deformatiile specifice respective, se dezvolta in conformitate cu curbele caracteristice s e ale betonului, respectiv ale otelului din armatura.
Putem intalni trei situatii de comportare, in functie de marimea solicitarii exterioare :
Situatia 1 : betonul din zona intinsa (sub axa neutra) nu fisureaza ;
Situatia 2 : betonul din zona intinsa (sub axa neutra) fisureaza, dar betonul din zona comprimata (deasupra axei neutre) lucreaza inca in stadiul elastic, avand deformatia specifica maxima ebc < 0,5 o oo (fata de ebcmax = 2 o oo deformatia maxima la compresiune si fata de ebu = 34 o oo deformatia ultima la compresiune) ; armaturile lucreaza in stadiul elastic.
Situatia 3 : betonul din zona intinsa (sub axa neutra) este fisurat, iar betonul din zona comprimata (deasupra axei neutre ) depaseste deformatia ebcmax de 2 o oo, putand ajunge in stadiul ultim de solicitare la compresiune ( ebu = 34 o oo), atingand deci ruperea in zona comprimata ; armaturile sunt solicitate dincolo de limita de curgere .
Avand in vedere ca in situatia 1, elementul de beton armat lucreaza in stadiul elastic pe intreaga inaltime a sectiunii, eforturile de intindere cat si cele de compresiune sunt preluate si de beton si de catre armatura.
In situatiile 2 si 3, betonul fisurat din zona intinsa (sub axa neutra) nu mai poate prelua eforturi de intindere (ebt = 0,1 o oo, iar Rt = 0), asa incat eforturile de intindere vor fi preluate numai de catre armatura. Eforturile de compresiune vor fi preluate insa de ambele materiale.
In fig.5.5 s-a notat :
sbc = efortul unitar maxim de compresiune in beton
sac = efortul unitar de compresiune in armatura Aac din zona comprimata
sat = efortul unitar de intindere in armatura Aat din zona intinsa
sb(y) = efortul unitar in beton, intr-o fibra aflata la distanta y fata de axa neutra
ebc = deformatia specifica a betonului la compresiune in fibra extrema, deasupra
axei neutre
eac = deformatia specifica a armaturii comprimate Aac
eat = deformatia specifica a armaturii intinse Aat
ey = deformatia specifica a betonului la o fibra aflata la distanta y de axa neutra
Eforturile din armatura (respectiv sac si sat) s-au figurat astfel incat sa indice valoarea lor mult superioara fata de eforturile unitare din beton (sb
Ariile diagramelor de eforturi unitare in beton reprezinta, in fapt, rezultantele eforturilor unitare de compresiune, respectiv de intindere din beton, adica fortele Cb si Tb.
Fortele din armatura se obtin prin inmultirea eforturilor unitare din armatura cu ariile respective de armatura - Aac si Aat rezultand Ca si Ta (fig. 5.6)
Fig. 5.6.
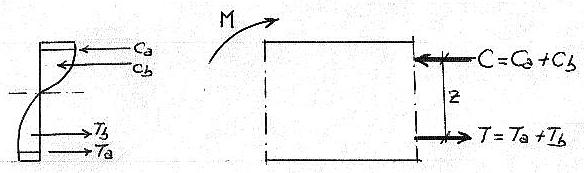
Din fig.5.6 se observa ca forta totala interioara de compresiune este C = Ca + Cb, iar forta totala interioara de intindere este T = Ta + Tb .
Cele doua rezultante sunt, evident, egale si de sens contrar (C = T), formand un cuplu interior
M = Cz = Tz, unde z = bratul de parghie al acestui cuplu. Momentul (cuplul) rezistent M echilibreaza momentul fortelor exterioare aplicate pe bara.
Acesta este principiul de baza in dimensionarea sectiunilor de beton armat si permite punerea in evidenta a modului de comportare a celor doua materiale asociate, dintre care unul (betonul) se plastifica in zona intinsa a sectiunii, prin fisurare, astfel incat, la un moment dat, Tb=0, betonul nemaipreluand intinderi.
Situatia nr. 3 Calculul la rupere (in stadiul ultim)
Fig. 5.9.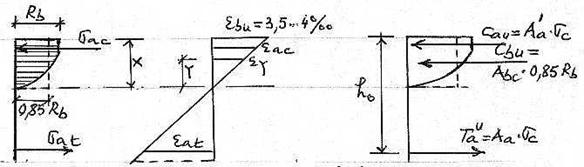 
Vom avea deci : ebu = 34 o oo eac > sc/Ea 2 o oo, eat > sat /Ea 2 o oo
Deci sac sat scurgere s c
Pentru cazul unei sectiuni dreptunghiulare simplu armate (armatura la partea intinsa) vom avea (fig. 5.10) :
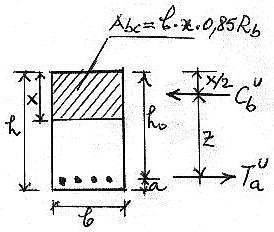Fig. 5.10.
In acest caz, forta ultima de compresiune in beton (la care betonul comprimat se rupe) va fi :
Cbu = Abc0,85Rb
iar pentru sectiunea dreptunghiulara va fi :
Cbu = 0,85Rbbx
Forta ultima in armatura va fi : Tau = Aasc
Proiectia fortelor pe axa barei :
Cbu - Tau = 0
0,85bxRb = Aasc
din care rezulta pozitia axei neutre:
Momentul
tuturor fortelor si cuplurilor fata de armatura
intinsa :
Mu = Cbu z
Mu = 0,85RbAbc(h0- x/2)
Se defineste inaltimea relativa a axei neutre prin raportul :
x = x/h0 = Aasc/0,85bh0Rb , dar Aa/bh0 = p si deci avem:
x = psc/0,85Rb
din care rezulta:
p = x *0,85Rb /sc
In urma experimentarilor s-a demonstrat ca pentru x 0,55, ruperea se produce prin beton, deci inaltimea axei neutre are o mare importanta in ceea ce priveste modul de rupere al elementului.
Din conditia x 0,55 care separa cele doua cazuri de rupere in conditii in care nu intervine efectul seismului, aceasta conduce la relatia :
plim = 0,55 0,85Rb/sc 0,45 Rb/sc , constituind un reper pentru procentul de armare, ca valoare limita.
In conditiile in care valoarea x = 0,25, vom avea :
plim 0,2Rb/sc
Pentru un beton B300 si otel PC60, vom avea in primul caz:
plim = 0.55*0.85*300/4000
iar in cel de-al doilea caz:
plim =0.25*0.85*300/4000
Ecuatia de momente pentru sectiunea dreptunghiulara simplu armata :
Mu = Cbu.z = 0,85bxRb(h0 x/2) = bh02 x x 0,85Rb (momentul fata de armatura intinsa)
sau:
Mu = Aasc(h0 x/2) (momentul fata de rezultanta compresiunilor in beton)
Pentru predimensionare, din relatia de mai sus, rezulta:
Aa = Mu/sc(h0-x/2)
Daca consideram h0 0,9h si x 0,3h, vom obtine:
formula aproximativa des utilizata pentru predimensionarea armaturii.
Trebuie sa se verifice conditia:
p < plim
In cazul neindeplinirii acestei conditii, este necesara armarea dubla, prevazand armatura si in zona comprimata.
Dupa cum s-a stabilit, momentul ultim (de rupere) pentru o sectiune simplu armata este
Mu = 0,85Rbbh02 x x . Daca se atribuie lui x valoarea xlim = 0,55 vom obtine :
Mu = 0,85Rbbh02 1/3bh02Rb
In stadiul elastic, momentul maxim este Mmax = sW0, unde W0 = 1/6bh02
Rezulta ca : Mumax = 2W0Rb, deci momentul ultim, in stadiul de rupere este dublu fata de momentul maxim in stadiul elastic.
|
Politica de confidentialitate | Termeni si conditii de utilizare |
Vizualizari: 3275
Importanta: 
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved
