| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Capacitatea calorica molara a gazelor reale
Variatia capacitatii calorice cu presiunea, la temperatura constanta, se poate stabili prin intermediul expresiei lui G (respectiv F) (v. exemplul XVI.2) sau prin integrarea ecuatiei stabilite din ecuatiile (XIV.6) si (XIV.41):
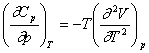
din care, prin integrare, se obtine::
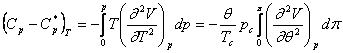
Potrivit ecuatiei pV = zRT:
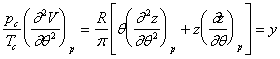
se obtine:
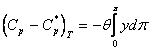
care permite o rezolvare grafica (v. diagrama VII.5). (Fig. XVI.4), stabilita pe baza acestei ecuatii, permite un calcul imediat al capacitatii calorice la diferite presiuni.
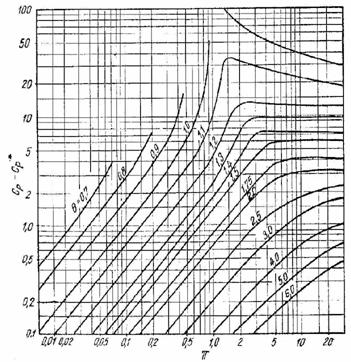
Fig. XVI.4. Diagrama (Cp - C*p)T pentru gaze si vapori
Exemplul 12. Sa se calculeze Cp, CV si Cp - CV pentru un gaz real a carui ecuatie de stare este de forma: pV = RT + Bp.
Rezolvare:
Conform relatiilor cunoscute, rezulta:
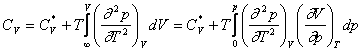
si
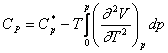
in care ![]() si
si ![]() sunt valorile capacitatilor calorice molare
ale gazului la p = 0, la aceeasi temperatura.
sunt valorile capacitatilor calorice molare
ale gazului la p = 0, la aceeasi temperatura.
Din ecuatia de
stare ![]() si
si ![]() se obtine:
se obtine:
![]() ;
; 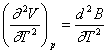
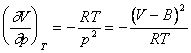

(neglijand termenul cu (V - B)-3).
Astfel, se obtine:
![]()
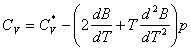
![]()
Exemplul 13. Sa se calculeze CV, Cp si Cp - CV pentru un gaz Berthelot (v. exemplul XVI.12).
Rezolvare:
Ecuatia lui Berthelot se poate scrie:
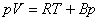
unde
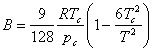
Rezulta:
![]()
![]()
Astfel, se obtine:
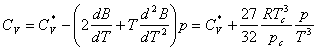
![]()
si
![]()
Exemplul 14. Sa se arate ca, pentru toate gazele a caror presiune variaza liniar cu temperatura, capacitatea calorica la volum constant este identica cu valoarea corespunzatoare a gazului perfect, la aceeasi temperatura (de exemplu gaz Van der Waals).
Rezolvare:
Deoarece
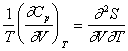
si
![]()
rezulta
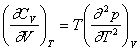
Pentru toate ecuatiile de stare in care p depinde liniar de T se poate scrie:
![]() sau
sau ![]()
Deoarece la limita ![]() ,
, ![]() , rezulta
, rezulta ![]() .
.
Aceasta relatie nu este verificata de experienta, ceea ce dovedeste din nou ca importanta ecuatiei lui Van der Waals este pur principala, fara o exactitate suficienta in calculele tehnice
Exemplul 15. Sa se calculeze variatia capacitatii calorice molare Cp a bioxidului de carbon la 100 oC, de la 1 la 100 atm presupunand valabila ecuatia lui Van der Waals.
Rezolvare:
Relatia de baza este:
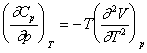
Din ecuatia lui Van der Waals se obtine:
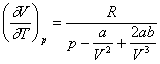 si
si 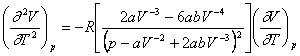
Prin integrarea primei ecuatii se obtine:
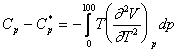
care se rezolva grafic. Cu datele a = 3,60 106,
b = 42,8, R = 82,1 (cm3, atm, mol) se determina valorile ![]() si
si 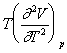 pentru diferitele valori ale lui p:
pentru diferitele valori ale lui p:
|
p atm |
V cm3 |
|
- |
p atm |
V cm3 |
|
- |
|
|
|
Prin integrare grafica se obtine:
![]()
Capacitatea calorica a bioxidului de carbon la 100 oC si 100 atm este:
![]()
Un rezultat apropiat se obtine cu ajutorul diagramei XVI.4.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2449
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved